Chapitre 1 Pourquoi apprenons-nous les statistiques ?
« Tu ne répondras pas à des questionnaires ou à des quiz sur les affaires du monde, ni ne passeras de tests. Tu ne t’assiéras pas avec des statisticiens, et tu ne commettras pas une science sociale »
- W.H. Auden2
1.1 Sur la psychologie des statistiques
À la surprise de nombreux étudiants, les statistiques représentent une part assez importante de l’enseignement en psychologie. À la surprise de personne, la statistique n’est que très rarement la partie préférée de l’enseignement en psychologie. Après tout, si vous aimiez vraiment l’idée de faire des statistiques, vous seriez probablement inscrit à un cours de statistique en ce moment, pas à un cours de psychologie. Il n’est donc pas surprenant qu’une proportion assez importante de la population étudiante ne soit pas satisfaite du fait que la psychologie comporte autant de statistiques. Dans ce contexte, j’ai pensé que le bon point de départ pourrait être de répondre à certaines des questions les plus courantes que les gens se posent au sujet des statistiques.
Une grande partie de cette question est liée à l’idée même de statistiques. Qu’est-ce que c’est ? C’est pour quoi faire ? Et pourquoi les scientifiques sont-ils si obsédés par ça ? Ce sont toutes de bonnes questions, quand on y pense. Commençons par la dernière. En tant que groupe, les scientifiques semblent bizarrement obsédés par la réalisation de tests statistiques sur tout. En fait, nous utilisons si souvent les statistiques que nous oublions parfois d’expliquer aux gens pourquoi nous le faisons. C’est une sorte d’acte de foi parmi les scientifiques - et en particulier les spécialistes des sciences sociales - que l’on ne peut pas faire confiance aux découvertes tant qu’on n’a pas fait quelques statistiques. On pourrait pardonner aux étudiants de premier cycle de penser que nous sommes tous complètement fous, parce que personne ne prend le temps de répondre à une question très simple :
Pourquoi faites-vous des statistiques ?
Pourquoi les scientifiques ne font-ils pas preuve de bon sens ?
C’est une question naïve à certains égards, mais la plupart des bonnes questions le sont. Il y a beaucoup de bonnes réponses,3 mais pour moi, la meilleure réponse est très simple : nous ne nous faisons pas assez confiance. Nous nous inquiétons d’êtres humains et sensibles à tous les préjugés, tentations et fragilités dont souffrent les humains. Une grande partie des statistiques est essentiellement une sauvegarde. Utiliser le « bon sens » pour évaluer les preuves, c’est se fier à son instinct, s’appuyer sur des arguments verbaux et utiliser la force brute de la raison humaine pour trouver la bonne réponse. La plupart des scientifiques ne pensent pas que cette approche puisse fonctionner.
En fait, à bien y penser, cela ressemble beaucoup à une question psychologique pour moi, et puisque je travaille dans un département de psychologie, il me semble que c’est une bonne idée de la creuser un peu plus ici. Est-il vraiment plausible de penser que cette approche de « bon sens » est très fiable ? Les arguments verbaux doivent être construits avec le langage, et toutes les langues ont des préjugés - certaines choses sont plus difficiles à dire que d’autres, et pas nécessairement parce qu’elles sont fausses (par exemple, l’électrodynamique quantique est une bonne théorie, mais difficile à expliquer en mots). Les intuitions de notre « instinct » ne sont pas faites pour résoudre des problèmes scientifiques, elles sont faites pour gérer des inférences quotidiennes - et comme l’évolution biologique est plus lente que les changements culturels, nous devrions dire qu’elles sont faites pour résoudre des problèmes quotidiens dans un monde différent de celui où nous vivons. Plus fondamentalement, le raisonnement exige des gens qu’ils s’engagent dans une « induction », qu’ils fassent des suppositions sages et qu’ils aillent au-delà de l’évidence immédiate des sens pour faire des généralisations sur le monde. Si vous pensez que vous pouvez le faire sans être influencé par divers distracteurs, eh bien, j’ai un pont à Londres que j’aimerais vous vendre. Comme nous le montrons dans la section suivante, nous ne pouvons même pas résoudre des problèmes « déductifs » (ceux pour lesquels il n’est pas nécessaire de deviner) sans être influencés par nos biais préexistants.
1.1.1 La malédiction des biais de croyance
Les gens sont plutôt intelligents. Nous sommes certainement plus intelligents que les autres espèces avec lesquelles nous partageons la planète (bien que beaucoup de gens puissent être en désaccord). Nos esprits sont des choses tout à fait étonnantes, et nous semblons être capables des exploits les plus incroyables de pensée et de raison. Mais ça ne nous rend pas parfaits. Et parmi les nombreuses choses que les psychologues ont montrées au fil des ans, il y a le fait que nous avons vraiment de la difficulté à être neutres, à évaluer les preuves de façon impartiale et sans être influencés par des préjugés préexistants. Un bon exemple en est le biais de croyance dans le raisonnement logique : si vous demandez aux gens de décider si un argument particulier est logiquement valide (c.-à-d. si la conclusion est vraie si les prémisses sont vraies), nous avons tendance à être influencés par la crédibilité de la conclusion, même lorsque nous ne le devrions pas. Par exemple, voici un argument valide dont la conclusion est crédible :
Toutes les cigarettes sont chères (Prémisse 1)
Certaines choses qui créent une dépendance sont peu coûteuses (Prémisse 2)
Par conséquent, certaines choses qui créent une dépendance ne sont pas des cigarettes (Conclusion)
Et voici un argument valide dont la conclusion n’est pas crédible :
Toutes les choses qui créent une dépendance coûtent cher (Prémisse 1)
Certaines cigarettes sont bon marché (Prémisse 2)
Par conséquent, certaines cigarettes ne créent pas de dépendance (Conclusion)
La structure logique de l’argument #2 est identique à celle de l’argument #1, et les deux sont valides. Toutefois, dans le deuxième argument, il y a de bonnes raisons de penser que la prémisse 1 est incorrecte et, par conséquent, il est probable que la conclusion est également incorrecte. Mais cela n’a rien à voir avec le sujet à l’étude ; un argument est déductiblement valable si la conclusion est une conséquence logique des prémisses. C’est-à-dire qu’un argument valide n’a pas besoin d’impliquer de vraies déclarations. Considérons maintenant un argument invalide qui a une conclusion crédible :
Toutes les choses qui créent une dépendance coûtent cher (Prémisse 1)
Certaines cigarettes sont bon marché (Prémisse 2)
Par conséquent,certaines choses qui créent une dépendance ne sont pas des cigarettes (Conclusion)
Et enfin, un argument invalide avec une conclusion non crédible :
Toutes les cigarettes sont chères (Prémisse 1)
Certaines choses qui créent une dépendance sont peu coûteuses (Prémisse 2)
Par conséquent,certaines cigarettes ne créent pas de dépendance (Conclusion)
Supposons maintenant que les gens soient parfaitement capables de mettre de côté leurs préjugés préexistants sur ce qui est vrai et ce qui ne l’est pas, et d’évaluer purement un argument sur ses mérites logiques. Nous nous attendrions à ce que 100 % des gens disent que les arguments valides sont valides, et à ce que 0 % des gens disent que les arguments invalides sont valides. Donc, si vous faite une expérience avec ces exemples, vous vous attendez à voir des données comme celle-ci :
| Conclusion perçue comme vraie | Conclusion perçue comme fausse | |
|---|---|---|
| Argument valide | 100 % disent qu’il est valide | 100 % disent qu’il est valide |
| Argument non valide | 0 % disent qu’il est valide | 0 % disent qu’il est valide |
Si les données psychologiques ressemblaient à ceci (ou même à une bonne approximation de ceci), nous pourrions nous sentir en sécurité en faisant simplement confiance à nos intuitions. Autrement dit, il serait tout à fait acceptable de laisser les scientifiques évaluer les données en fonction de leur bon sens, et de ne pas se préoccuper de toutes ces statistiques obscures. Cependant, vous avez pris des cours de psycho, et maintenant vous savez probablement où cela nous mènent.
Dans une étude classique, Evans, Barston et Pollard (1983) ont mené une expérience portant exactement sur cette question. Ce qu’ils ont découvert, c’est que lorsque les préjugés préexistants (c.-à-d. les croyances) étaient en accord avec la structure des données, tout allait comme on l’espérait :
| Conclusion perçue comme vraie | Conclusion perçue comme fausse | |
|---|---|---|
| Argument valide | 92 % disent qu’il est valide | |
| Argument non valide | 8 % disent qu’il est valide |
Ce n’est pas parfait, mais c’est assez bon. Mais regardez ce qui se passe quand nos croyances sur la vérité de la conclusion vont à l’encontre de la structure logique de l’argument :
| Conclusion perçue comme vraie | Conclusion perçue comme fausse | |
|---|---|---|
| Argument valide | 92 % disent qu’il est valide | 44 % disent qu’il est valide |
| Argument non valide | 92 % disent qu’il est valide | 8 % disent qu’il est valide |
Mince, ce n’est pas aussi bon. Apparemment, lorsqu’on présente aux gens un argument solide qui contredit nos croyances préexistantes, nous trouvons qu’il est assez difficile de le percevoir comme un argument solide (les gens ne le faisaient que 46 % du temps). Pire encore, lorsqu’on présente aux gens un argument faible qui correspond à nos préjugés préexistants, presque personne ne peut voir que l’argument est faible (les gens se trompent 92 % du temps !).4
Si vous y réfléchissez, ce n’est pas comme si ces données étaient terriblement accablantes. Dans l’ensemble, les gens ont fait mieux que par hasard pour compenser leurs préjugés antérieurs, car environ 60 % des jugements des gens étaient exacts (on s’attendrait à ce que 50 % le soient avec le hasard). Malgré tout, si vous étiez un « évaluateur professionnel des données probantes « et que quelqu’un vous offrait un outil magique qui augmente vos chances de prendre la bonne décision de 60 % à 95 %, vous sauteriez probablement sur l’occasion, non ? Bien sûr que vous le feriez. Heureusement, nous avons un outil qui nous permet de le faire. Mais ce n’est pas de la magie, ce sont des statistiques. C’est donc la raison pour laquelle les scientifiques adorent les statistiques. C’est trop facile pour nous de « croire ce que nous voulons croire ». Donc, si nous voulons « croire aux données », nous allons avoir besoin d’un peu d’aide pour garder nos préjugés personnels sous contrôle. C’est ce que font les statistiques, ça nous aide à rester honnêtes.
1.2 La mise en garde contre le paradoxe de Simpson
Ce qui suit est une histoire vraie (je pense !). En 1973, l’Université de Californie, à Berkeley, s’inquiétait de l’admission d’étudiants dans leurs cours de troisième cycle. Plus précisément, ce qui a causé le problème, c’est la répartition par sexe de leurs admissions, qui ressemblait à ceci :
| Nombre de candidats | Pourcentage d’admis | |
|---|---|---|
| Hommes | 8442 | 44% |
| Femmes | 4321 | 35% |
Compte tenu de cela, ils craignaient d’être poursuivis en justice !5 Étant donné qu’il y avait près de 13 000 candidats, une différence de 9 % dans les taux d’admission entre les hommes et les femmes est beaucoup trop grande pour que ce soit une coïncidence. Des données assez convaincantes, n’est-ce pas ? Et si je vous disais que ces données reflètent en fait un faible biais en faveur des femmes (en quelque sorte !), vous penseriez probablement que je suis soit folle, soit sexiste.
Bizarrement, c’est en fait en partie vrai. Lorsque les gens ont commencé à examiner plus attentivement les données sur les admissions, ils ont rapporté une histoire assez différente (Bickel, Hammel, and O’Connell 1975). Plus précisément,lorsqu’ils l’ont examiné département par département, il s’est avéré que la plupart des départements avaient en fait un taux de réussite légèrement plus élevé pour les femmes que pour les hommes. Le tableau ci-dessous indique le nombre d’admissions pour les six plus grands départements (les noms des départements ont été supprimés pour des raisons de confidentialité) :
| Hommes | Femmes | |||
|---|---|---|---|---|
| Département | Candidats | Pourcentage d’admissions | Candidates | Pourcentage d’admissions |
| A | 825 | 62% | 108 | 82% |
| B | 560 | 63% | 25 | 68% |
| C | 325 | 37% | 593 | 34% |
| D | 417 | 33% | 375 | 35% |
| E | 191 | 28% | 393 | 24% |
| F | 272 | 6% | 341 | 7% |
Fait remarquable, la plupart des départements avaient un taux d’admission plus élevé pour les femmes que pour les hommes ! Pourtant, le taux global d’admission à l’université était plus faible chez les femmes que chez les hommes. Comment est-ce possible ? Comment ces deux affirmations peuvent-elles être vraies en même temps ?
Voilà ce qui se passe. Tout d’abord, notons que les départements ne sont pas égaux entre eux en termes de pourcentage d’admission : certains départements (par exemple, A, B) avaient tendance à admettre un pourcentage élevé de candidats qualifiés, alors que d’autres (par exemple, F) avaient tendance à rejeter la plupart des candidats, même si ceux-ci étaient de grande qualité. Ainsi, parmi les six départements indiqués ci-dessus, notez que le département A est le plus généreux, suivi de B, C, D, E et F dans cet ordre. Ensuite, remarquez que les hommes et les femmes avaient tendance à candidater dans des départements différents. Si nous classons les départements en fonction du nombre total de candidats masculins reçus, nous obtenons A>B>D>C>F>E (les départements « faciles » sont en gras). Dans l’ensemble, les hommes avaient tendance à présenter une demande dans les départements où le taux d’admission était élevé. Maintenant, comparez ceci à la façon dont les candidates se sont distribuées. En classant les départements en fonction du nombre total de candidatures féminines, on obtient un classement tout à fait différent : C>E>D>F>A>B. En d’autres termes, ce que ces données semblent suggérer, c’est que les candidates avaient tendance à postuler dans des départements « plus durs ». En fait, si nous regardons la Figure 1‑1, nous constatons que cette tendance est systématique et assez frappante. Cet effet est connu sous le nom de paradoxe de Simpson. Ce n’est pas courant, mais cela arrive dans la vraie vie, et la plupart des gens en sont très surpris lorsqu’ils le rencontrent pour la première fois, et beaucoup de gens refusent même de croire que c’est réel. C’est très réel. Bien que beaucoup de leçons statistiques très subtiles sont dissimulées derrière ce fait, je veux m’en servir pour souligner un point beaucoup plus important : il est difficile de faire de la recherche et il y a beaucoup de pièges subtils et contre-intuitifs qui attendent les personnes imprudentes. C’est la deuxième raison pour laquelle les scientifiques adorent les statistiques et pour laquelle nous enseignons les méthodes de recherche. Parce que la science est difficile et que la vérité est parfois astucieusement cachée dans les coins et les recoins de données complexes.
Avant d’en terminer avec ce sujet, j’aimerais souligner une autre chose vraiment critique qui est souvent négligée dans un cours de méthodologie de la recherche. Les statistiques ne résolvent qu’une partie du problème. Rappelez-vous que nous avons commencé tout cela avec la crainte que les processus d’admission de Berkeley pourraient être injustement biaisés à l’encontre des candidates. Lorsque nous avons examiné les données « agrégées », il nous a semblé que l’université faisait de la discrimination à l’égard des femmes, mais lorsque nous « désagrégeons » et que nous examinons le comportement individuel de tous les départements, il s’avère que les départements eux-mêmes étaient, le cas échéant, légèrement biaisés en faveur des femmes.
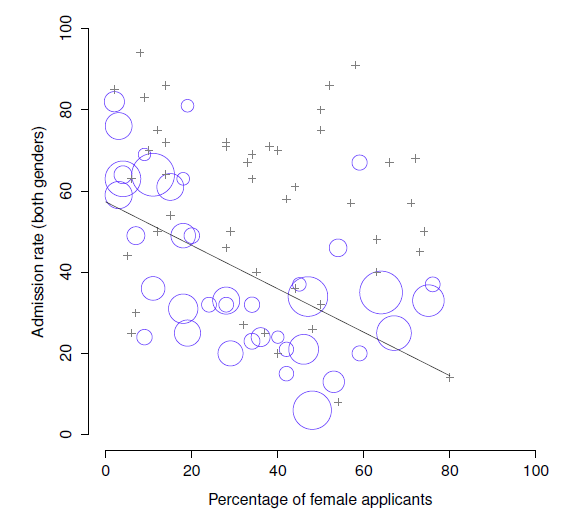
Figure 1‑1 : Les données de Berkeley 1973 sur les admissions à l’université. Ce chiffre représente le taux d’admission pour les 85 départements qui comptaient au moins une femme candidate, en fonction du pourcentage de femmes candidates. Le graphique est un remaniement de la figure 1 de Bickel, Hammel et O’Connell (1975). Les cercles représentent les départements qui comptent plus de 40 candidats ; la superficie du cercle est proportionnelle au nombre total de candidats. Le graphique représente les départements qui comptent moins de 40 candidats.
Le biais sexiste dans le nombre total d’admissions était dû au fait que les femmes avaient tendance à candidater dans les départements plus difficile. D’un point de vue juridique, cela met probablement l’université à l’abri. Les admissions aux études supérieures sont déterminées au niveau de chaque département et il y a de bonnes raisons de le faire. Au niveau des différents départements, les décisions sont plus ou moins impartiales (le biais en faveur des femmes à ce niveau est faible et n’est pas uniforme dans tous les départements). Étant donné que l’université ne peut pas dicter les départements auxquels les gens choisissent de s’adresser et que la prise de décision se fait au niveau du département, elle ne peut guère être tenue responsable des biais que ces choix produisent.
C’est ce qui a motivé les remarques quelque peu désinvoltes que j’ai faites précédemment, mais ce n’est pas le problème. Après tout, si cela nous intéresse d’un point de vue plus sociologique et psychologique, nous pourrions nous demander pourquoi il y a de si grandes différences entre les genres en ce qui concerne les candidatures. Pourquoi les hommes ont-ils tendance à s’inscrire plus souvent que les femmes au programme d’ingénieur, et pourquoi cette tendance s’inverse-t-elle pour le département d’anglais ? Pourquoi les départements qui ont tendance à avoir un biais pour les demandes d’admission des femmes ont-ils tendance à avoir des taux d’admission globaux inférieurs à ceux des départements qui ont un biais pour les demandes des hommes ? Ne s’agit-il pas là d’un préjugé sexiste, même si tous les départements sont eux-mêmes impartiaux ? C’est possible. Posons, hypothétiquement, que les hommes préfèrent les « sciences dures » et que les femmes préfèrent les « sciences humaines ». Supposons en outre que la raison pour laquelle les départements des humanités ont de faibles taux d’admission est que le gouvernement ne veut pas financer les humanités (les places de doctorat, par exemple, sont souvent liées aux projets de recherche financés par le gouvernement). Est-ce que cela constitue un préjugé sexiste ? Ou simplement une vision non éclairée de la valeur des sciences humaines ? Que ce passerait-il si quelqu’un de haut placé au sein du gouvernement coupait les fonds des humanités parce qu’il estimait que les humanités sont des « choses inutiles pour les nanas » ? Cela semble assez ouvertement sexiste. Rien de tout cela ne relève de la statistique, mais c’est important pour le projet de recherche. Si vous vous intéressez aux effets structurels globaux des subtils préjugés sexistes, vous souhaiteriez probablement examiner à la fois les données agrégées et désagrégées. Si vous êtes intéressé par le processus de prise de décision à Berkeley même, vous n’êtes probablement intéressé que par les données désagrégées.
Bref, il y a beaucoup de questions critiques auxquelles vous ne pouvez pas répondre avec des statistiques, mais les réponses à ces questions auront un impact énorme sur la façon dont vous analyserez et interpréterez les données. C’est la raison pour laquelle vous devriez toujours considérer les statistiques comme un outil pour vous aider à mieux connaître vos données. Ni plus ni moins. C’est un outil puissant à cette fin, mais rien ne peut remplacer une réflexion approfondie.
1.3 Statistiques en psychologie
J’espère que la discussion ci-dessus a contribué à expliquer pourquoi la science en général est si axée sur les statistiques. Mais je suppose que vous vous posez beaucoup plus de questions sur le rôle que jouent les statistiques en psychologie, et plus précisément pourquoi les programmes de psychologie consacrent toujours autant de cours aux statistiques. Voici donc ma tentative pour répondre à quelques-unes d’entre elles…
Pourquoi la psychologie a-t-elle autant de statistiques ?
Pour être tout à fait honnête, il y a plusieurs raisons dont certaines sont meilleures que d’autres. La raison la plus importante est que la psychologie est une science statistique. Ce que j’entends par là, c’est que les « choses » que nous étudions sont des personnes. Des gens réels, compliqués, glorieusement désordonnés, furieusement pervers. Les « choses » de la physique incluent les objets comme les électrons, et bien qu’il y ait toutes sortes de complexités qui surgissent en physique, les électrons n’ont pas leur propre esprit. Ils n’ont pas d’opinions, ils ne diffèrent pas les uns des autres de façon bizarre et arbitraire, ils ne s’ennuient pas au milieu d’une expérience, et ils ne se fâchent pas contre l’expérimentateur et n’essaient pas délibérément de saboter les données (non pas que je l’ai jamais fait !). Au fond, la psychologie est plus difficile que la physique.6
Fondamentalement, nous vous enseignons les statistiques en tant que psychologues parce que vous devez être meilleurs en statistiques que les physiciens. Il y a en fait un dicton utilisé parfois en physique, selon lequel « si votre expérience a besoin de statistiques, vous auriez dû faire une meilleure expérience ». Ils ont le luxe de pouvoir dire cela parce que leurs objets d’étude sont d’une simplicité pathétique par rapport au vaste désordre auquel sont confrontés les spécialistes des sciences sociales. Et ce n’est pas seulement la psychologie. La plupart des sciences sociales dépendent désespérément des statistiques. Pas parce que nous sommes de mauvais expérimentateurs, mais parce que nous avons choisi un problème plus difficile à résoudre. Nous vous enseignons les statistiques parce que vous en avez vraiment, vraiment besoin.
Quelqu’un d’autre ne peut-il pas faire les statistiques ?
Dans une certaine mesure, mais pas complètement. Il est vrai qu’il n’est pas nécessaire de devenir un statisticien pleinement formé uniquement pour faire de la psychologie, mais qu’il faut atteindre un certain niveau de compétence statistique. À mon avis, il y a trois raisons pour lesquelles tout chercheur en psychologie devrait être en mesure de faire des statistiques de base :
Premièrement, il y a la raison fondamentale : les statistiques sont étroitement liées à la conception de la recherche. Si vous voulez être bon dans la conception d’études psychologiques, vous devez à tout le moins comprendre les bases des statistiques.
Deuxièmement, si vous voulez être bon du point de vue de la recherche en psychologie, vous devez être capable de comprendre la littérature psychologique. Mais presque tous les articles de la littérature psychologique rapportent les résultats d’analyses statistiques. Donc, si vous voulez vraiment comprendre la psychologie, vous devez être capable de comprendre ce que d’autres personnes ont fait avec leurs données. Et cela signifie comprendre un certain nombre de statistiques.
Troisièmement, il y a un gros problème pratique à dépendre d’autres personnes pour faire toutes vos statistiques : l’analyse statistique coûte cher. Si vous vous ennuyez et que vous voulez savoir combien le gouvernement australien demande pour les frais universitaires, vous remarquerez quelque chose d’intéressant : les statistiques sont désignées comme une catégorie « priorité nationale », et donc les frais sont beaucoup, beaucoup plus bas que pour tout autre domaine d’études. C’est parce qu’il y a une pénurie massive de statisticiens. Donc, de votre point de vue de chercheur en psychologie, les lois de l’offre et de la demande ne sont pas exactement de votre côté ! Par conséquent, chaque fois que vous voudrez faire de la recherche en psychologie, la réalité cruelle vous rappellera que vous n’avez pas assez d’argent pour payer un statisticien. L’économie de la situation signifie donc qu’il faut être assez autosuffisant.
Il est à noter qu’un grand nombre de ces raisons se généralisent au-delà des chercheurs. Si vous voulez être un psychologue praticien et rester à la pointe du domaine, il est utile de pouvoir lire la littérature scientifique, qui repose en grande partie sur les statistiques.
- Je me fiche des emplois, de la recherche ou du travail clinique. Ai-je besoin de statistiques ?
D’accord, maintenant vous vous moquez de moi. Pourtant, je pense que ça devrait compter pour vous aussi. Les statistiques devraient compter pour vous de la même façon que les statistiques devraient compter pour tout le monde. Nous vivons au XXIe siècle, et les données sont partout. Franchement, étant donné le monde dans lequel nous vivons de nos jours, une connaissance de base des statistiques s’apparente à un outil de survie ! C’est le sujet de la section suivante.
1.4 Statistiques dans la vie quotidienne
“Nous nous noyons dans l’information, mais nous sommes affamés de connaissances” - Divers auteurs, original probablement John Naisbitt
Lorsque j’ai commencé à rédiger mes notes de cours, j’ai pris les 20 articles les plus récents affichés sur le site Web d’ABC. Sur ces 20 articles, il s’est avéré que 8 d’entre eux portaient sur un sujet que j’appellerais un sujet statistique et que 6 d’entre eux comportaient une erreur. L’erreur la plus courante, si vous êtes curieux, était de ne pas avoir rapporté les données de base (par exemple, l’article mentionne que 5 % des personnes dans la situation X ont une caractéristique Y, mais ne dit pas à quel point cette caractéristique est commune à tous les autres ! Ce que j’essaie de dire ici, ce n’est pas que les journalistes sont mauvais en statistiques (bien qu’ils le soient presque toujours), c’est qu’une connaissance de base des statistiques est très utile pour essayer de comprendre quand quelqu’un d’autre fait une erreur ou même vous ment. En fait, l’une des plus importantes choses qu’une connaissance des statistiques vous apporte est de vous mettre en colère contre un journal ou un site Internet beaucoup plus souvent. Vous en trouverez un bon exemple à la section 4.1.5. Dans les versions ultérieures de ce livre, j’essaierai d’inclure plus d’anecdotes en ce sens.
1.5 Les méthodes de recherche ne se limitent pas aux statistiques
Jusqu’à présent, j’ai surtout parlé de statistiques, et il vous serait donc pardonné de penser que les statistiques sont tout ce qui m’importe dans la vie. Pour être juste, vous n’auriez pas tort, mais la méthodologie de recherche est un concept plus large que les statistiques. Ainsi, la plupart des cours de méthodologie de la recherche couvriront un grand nombre de sujets qui se rapportent beaucoup plus à la pratique de la conception de la recherche, et en particulier les questions que vous rencontrez lorsque vous essayez de faire de la recherche avec des humains. Cependant, environ 99 % des craintes des étudiants ont trait à la partie statistique du cours, alors je me suis concentré sur les statistiques dans cette discussion, et j’espère vous avoir convaincu que les statistiques sont importantes et, surtout, qu’il ne faut pas en avoir peur. Cela dit, il est assez typique que les cours d’introduction aux méthodes de recherche soient très riches en statistiques. Ce n’est pas (habituellement) parce que les enseignants sont mauvais. C’est plutôt le contraire. Les cours d’introduction se concentrent beaucoup sur les statistiques parce que vous avez presque toujours besoin de statistiques avant d’avoir besoin d’une formation sur les autres méthodes de recherche. Pourquoi ? Parce que presque tous vos travaux dans d’autres classes reposeront sur la formation en statistique, dans une bien plus grande mesure qu’ils ne reposent sur d’autres outils méthodologiques. Il n’est pas courant que les travaux de premier cycle exigent que vous conceviez votre propre étude à partir de toutes pièces (auquel cas vous auriez besoin d’en savoir beaucoup sur la conception de la recherche), mais il est courant que vous deviez analyser et interpréter des données recueillies dans une étude qu’un tiers a conçue (auquel cas vous devez disposer de statistiques). En ce sens et afin de vous permettre de réussir dans tous vos autres cours, connaitre les statistiques est urgent.
Mais notez que « urgent » est différent de « important » - les deux sont importants. Je tiens vraiment à souligner que la conception de la recherche est tout aussi importante que l’analyse des données, et ce livre y consacre beaucoup de temps. Cependant, bien que les statistiques aient une sorte d’universalité et fournissent un ensemble d’outils de base qui sont utiles pour la plupart des types de recherche, en psychologie, les méthodes de recherche ne sont pas aussi universelles. Il y a quelques principes généraux auxquels tout le monde devrait réfléchir, mais une grande partie de la conception de la recherche est très idiosyncrasique et propre au domaine de recherche dans lequel vous voulez vous engager. Dans la mesure où ce sont les détails qui sont significatifs, ils n’apparaissent généralement pas dans les statistiques d’introduction et les cours de méthodologie de recherche.
References
Bickel, P. J., E. A. Hammel, and J. W. O’Connell. 1975. “Sex Bias in Graduate Admissions: Data from Berkeley.” Science 187 (4175): 398–404. https://doi.org/10.1126/science.187.4175.398.
La citation provient du poème d’Auden de 1946 Under Wich Lyre : A Reactionary Tract for the Times, prononcé dans le cadre d’un discours d’ouverture à l’Université Harvard. L’histoire du poème est intéressante : http://harvardmagazine.com/2007/11/a-poets-warning.html↩︎
Y compris la suggestion que le bon sens fait défaut parmi les scientifiques.↩︎
Dans mes moments les plus cyniques, j’ai l’impression que ce seul fait explique 95% de ce que je lis sur internet.↩︎
Des versions antérieures de ces notes laissaient entendre, à tort, qu’elles faisaient l’objet d’une poursuite. Mais ce n’est pas vrai. Il y a un joli commentaire à ce sujet ici : https://www.refsmmat.com/posts/2016-05-08-simpsons-paradox-berkeley.html. Un grand merci à Wilfried Van Hirtum de me l’avoir signalé.↩︎
Ce qui pourrait expliquer pourquoi la physique est un peu plus avancée que nous en tant que science.↩︎