Chapitre 11 Comparer deux moyennes

Au chapitre 10, nous avons examiné la situation où votre variable résultat a une échelle nominale et votre variable prédictive est également l’échelle nominale. Beaucoup de situations réelles sont ainsi, et vous constaterez que les tests du chi carré en particulier sont très largement utilisés. Cependant, vous êtes beaucoup plus susceptible de vous retrouver dans une situation où votre variable résultat est une échelle d’intervalle ou plus, et ce qui vous intéresse est de savoir si la valeur moyenne de la variable de résultat est plus élevée dans un groupe ou un autre. Par exemple, un psychologue pourrait vouloir savoir si les niveaux d’anxiété sont plus élevés chez les parents que chez les non-parents, ou si la capacité de mémoire de travail est réduite en écoutant de la musique (par rapport à ne pas écouter de musique). Dans un contexte médical, nous pourrions vouloir savoir si un nouveau médicament augmente ou diminue la tension artérielle. Un agronome pourrait vouloir savoir si l’ajout de phosphore aux plantes indigènes australiennes les tuera.⁷⁹ Dans toutes ces situations, notre variable de résultat est une variable d’échelle d’intervalle ou de rapport continue, et notre prédicteur est une variable binaire de « regroupement ». En d’autres termes, nous voulons comparer les moyennes des deux groupes.

La réponse standard au problème de la comparaison des moyens est d’utiliser un test t, dont il existe plusieurs variantes en fonction de la question à laquelle vous voulez répondre. Par conséquent, la majeure partie de ce chapitre se concentre sur différents types de tests t : un test t sur un échantillon est discuté à la section 11.2, les tests t pour échantillons indépendants sont discutés aux sections 11.3 et 11.4, et les tests t pour échantillons appariés sont discutés à la section 11.5. Nous parlerons ensuite des tests unilatéraux (Section 11.6) et, après cela, nous parlerons un peu du d de Cohen, qui est la mesure standard de l’ampleur de l’effet pour un test t (Section 11.7). Les sections suivantes du chapitre se concentrent sur les hypothèses des tests t et sur les recours possibles en cas de violation de ces tests. Cependant, avant de discuter de ces choses utiles, nous allons commencer par une discussion sur les tests z.

11.1 Le z-test pour un échantillon

Dans cette section, je décrirai l’un des tests les plus inutiles de toutes les statistiques : le test z. Sérieusement, ce test n’est presque jamais utilisé dans la vie réelle. Son seul but réel est que, dans l’enseignement des statistiques, c’est un tremplin très pratique vers le test t, qui est probablement l’outil le plus (trop) utilisé dans toutes les statistiques.

11.1.1 Le problème d’inférence auquel le test s’adresse

Pour introduire l’idée derrière le test z, prenons un exemple simple. Un de mes amis, le Dr Zeppo, note son cours d’introduction à la statistique sur une courbe. Supposons que la note moyenne dans sa classe est de 67,5 et que l’écart-type est de 9,5. Parmi ses centaines d’étudiants, il s’avère que 20 d’entre eux suivent aussi des cours de psychologie. Par curiosité, je me demande si les étudiants en psychologie ont tendance à obtenir les mêmes notes que tout le monde (c.-à-d. 67,5 en moyenne) ou s’ils ont tendance à obtenir des notes plus ou moins élevées ? Il m’envoie par courriel le fichier zeppo.csv, que j’utilise pour examiner les notes de ces étudiants, dans le tableur Jamovi,

50 60 60 64 66 66 67 69 70 74 76 76 77 79 79 79 81 82 82 89

puis calculez la moyenne dans « Exploration » -« Descriptifs » [Pour ce faire, j’ai dû changer le niveau de mesure de X en « Continu », car lors de l’ouverture / importation du fichier csv, Jamovi en a fait une variable de niveau nominal, ce qui n’est pas correct pour mon analyse.]. La valeur moyenne est de 72,3.

Bien. Il se peut que les étudiants en psychologie obtiennent des résultats légèrement supérieurs à la normale. Cette moyenne d’échantillon de \(\bar{X} = 72,3\) est un peu plus élevée que la moyenne de population supposée de \(\mu=67.5\) par ailleurs, une taille d’échantillon de N=20 n’est pas si grande. C’est peut-être un hasard.

Pour répondre à la question, il est utile de pouvoir écrire ce que je crois savoir. Premièrement, je sais que la moyenne de l’échantillon est \(\bar{X} = 72,3\). Si je suis prêt à supposer que les étudiants en psychologie ont le même écart-type que le reste de la classe, je peux dire que l’écart-type de la population est \(\sigma= 9,5\). Je supposerai aussi que puisque le Dr Zeppo évalue les étudiants dont les notes suivent une courbe qui est normalement distribuée.

Ensuite, il est utile d’être clair sur ce que je veux apprendre des données. Dans ce cas, mon hypothèse de recherche porte sur la moyenne de la population µ des notes des étudiants en psychologie, laquelle est inconnu. Plus précisément, je veux savoir si \(\mu =67,5\) ou non. Étant donné que c’est ce que je sais, pouvons-nous concevoir un test d’hypothèse pour résoudre notre problème ? Les données, ainsi que la distribution hypothétique dont on pense qu’elles proviennent, sont présentées à la Figure 11‑1. Ce qui constitue la bonne réponse n’est pas du tout évident, n’est-ce pas ? Pour cela, nous allons avoir besoin de statistiques.

11.1.2 Construire le test d’hypothèse

La première étape de la construction d’un test d’hypothèse consiste à déterminer clairement ce que sont les hypothèses nulles et alternatives. Ce n’est pas trop difficile à faire. Notre hypothèse nulle, H₀, est que la moyenne réelle de la population µ pour les notes des étudiants en psychologie est de 67,5, et notre hypothèse alternative est que la moyenne de la population n’est pas de 67,5. Si nous écrivons ceci en notation mathématique, ces hypothèses deviennent :

\[\text{H}_{0}: \mu = 67,5\\ \text{H}_{1}: \mu\neq 67,5\]

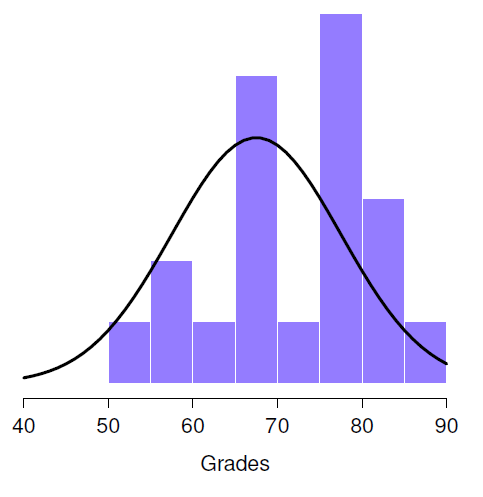
Figure 11‑1 : La distribution théorique (ligne pleine) à partir de laquelle les notes des étudiants en psychologie (barres) sont censées avoir été générées.

bien que pour être honnête, cette notation n’ajoute pas grand-chose à notre compréhension du problème, c’est juste une façon compacte d’écrire ce que nous essayons d’apprendre à partir des données. Les hypothèses nulles H₀ et l’hypothèse alternative H₁ de notre test sont toutes deux illustrées à la Figure 11‑2. En plus de nous fournir ces hypothèses, le scénario décrit ci-dessus nous fournit une bonne quantité de connaissances de base qui pourraient être utiles. Plus précisément, il y a deux éléments d’information particuliers que nous pouvons ajouter :

1. Les notes en psychologie sont normalement distribuées.
2. L’écart-type réel de ces scores \(\sigma\) est connu pour être 9,5.

Pour l’instant, nous allons agir comme si ce sont des faits absolument dignes de confiance. Dans la vraie vie, ce genre de connaissances de base absolument dignes de confiance n’existe pas, et donc si nous voulons nous fier à ces faits, nous devrons simplement supposer que ces choses sont vraies. Toutefois, comme ces hypothèses peuvent être justifiées ou non, nous devrons peut-être les vérifier. Mais pour l’instant, nous nous allons faire simple.

L’étape suivante consiste à déterminer ce qui considérerions comme un bon choix pour une statistique de test, quelque chose qui nous aiderait à faire la distinction entre H₀ et H₁. Étant donné que les hypothèses se réfèrent toutes à la moyenne de la population \(\mu\), vous seriez assez confiant que la moyenne de l’échantillon \(\bar{X}\) constituerait un point de départ très utile. Ce que nous pourrions faire, c’est examiner la différence entre la moyenne de l’échantillon \(\bar{X}\) et la valeur moyenne que l’hypothèse nulle prédit pour la population.

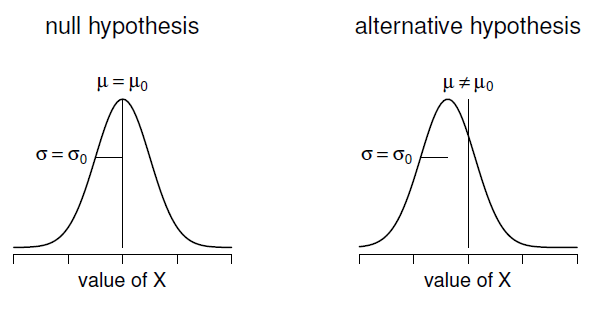
Figure 11‑2 : Illustration graphique de l’hypothèse nulle et de l’hypothèse alternative supposée par le z-test à un échantillon. L’hypothèse nulle et l’hypothèse alternative supposent toutes deux que la distribution de la population est normale et supposent en outre que l’écart-type de la population est connu (fixé à une certaine valeur \(\sigma_{0}\)). L’hypothèse nulle (à gauche) est que la moyenne de population µ est égale à une valeur donnée \(\mu_{0}\). L’hypothèse alternative est que la moyenne de population diffère de cette valeur, \(\mu-\mu_{0}\).

Dans notre exemple, cela signifie que nous calculons \(\bar{X} - 67,5\). Plus généralement, si nous posons que \(\mu_{0}\) correspond à la valeur de la moyenne de notre population selon l’hypothèse nulle, alors nous devrions calculer

\[ \bar{X} - \mu_{0} \]

Si cette quantité est égale ou très proche de 0, les choses s’annoncent bien pour l’hypothèse nulle. Si cette quantité est très éloignée de 0, il est moins probable que l’hypothèse nulle vaille la peine d’être retenue. Mais à quelle distance de zéro doit-on s’éloigner pour rejeterH₀?

Pour comprendre cela, nous devons être un peu plus rusés, et nous devons faire le lien avec deux connaissances de base que j’ai présentées précédemment, à savoir que les données brutes sont normalement distribuées et que nous connaissons la valeur de l’écart-type de la population \(\sigma\). Si l’hypothèse nulle est vraie et que la vraie moyenne est \(\mu_{0}\), alors ces faits réunis nous indiquent la distribution de la population : une distribution normale ayant pour moyenne \(\mu_{0}\) et pour écart-type \(\sigma\). En adoptant la notation de la section 7.5, un statisticien pourrait écrire ceci sous la forme :

\[ X \sim Normale(\mu_{0},\sigma^{2}) \]

Bien, si c’est vrai, alors que dire de la distribution de \(\bar{X}\)? Comme nous l’avons mentionné précédemment (voir la section 8.3.3), la distribution d’échantillonnage de la moyenne \(\bar{X}\) est également normale et a une moyenne \(\mu\). Mais l’écart-type de cette distribution d’échantillonnage \(SE(\bar{X})\), qu’on appelle l’erreur type de la moyenne, est

\[ SE\left( \bar{X} \right) = \frac{\sigma}{\sqrt{N}} \]

En d’autres termes, si l’hypothèse nulle est vraie, la distribution d’échantillonnage de la moyenne peut s’écrire comme suit :

\[ \bar{X} \sim Normale(\mu_{0},SE(\bar{X})) \]

Maintenant, le tour est joué. Ce que nous pouvons faire, c’est convertir la moyenne de l’échantillon \(\bar{X}\) en un score standard (Section 4.5). Cela s’écrit conventionnellement comme z, mais pour l’instant je vais le noter \(z_{\bar{X}}\). (La raison de l’utilisation de cette notation étendue est de vous aider à vous rappeler que nous calculons une version standardisée d’une moyenne d’échantillon, et non une version standardisée d’une seule observation, ce à quoi un z-score fait habituellement référence). Lorsque nous le faisons, le score z de la moyenne de notre échantillon est le suivant

\[ z_{\bar{X}} = \frac{\bar{X} - \mu_{0}}{SE(\bar{X})} \]

ou, de manière équivalente

\[ z_{\bar{X}}=\frac{\bar{X}-\mu_{0}}{\sigma/\sqrt{N}} \]

Ce z-score est notre statistique de test. Ce qu’il y a d’intéressant à utiliser cette statistique comme statistique de test, c’est que, comme tous les z-scores, elle a une distribution normale standard :

\[ z \sim Normale(1,0) \]

(encore une fois, voir la Section 4.5 si vous avez oublié pourquoi c’est vrai). En d’autres termes, quelle que soit l’échelle sur laquelle se trouvent les données d’origine, la statistique z elle-même a toujours la même interprétation : elle est égale au nombre d’erreurs-types qui séparent la moyenne observée de l’échantillon \(\bar{X}\) de la moyenne de la population \(\mu_{0}\) prévue par l’hypothèse nulle. Mieux encore, quels que soient les paramètres de population pour les scores bruts, les 5 % de régions critiques pour le test z sont toujours les mêmes, comme l’illustre la Figure 11‑3. Et ce que cela signifiait, à l’époque où les gens faisaient toutes leurs statistiques à la main, c’est que quelqu’un pouvait publier un tableau comme celui-ci :

	valeur critique z
niveau de significativité \(\alpha\)	test bilatéral	test unilatéral
.1	1.644854	1.281552
.05	1.959964	1.644854
.01	2.575829	2.326348
.001	3.290527	3.090232

Cela permettait aux chercheurs de calculer leur statistique z à la main et ensuite rechercher la valeur critique dans un manuel scolaire.

11.1.3 Un exemple travaillé à la main

Comme je l’ai mentionné plus tôt, le z-test n’est presque jamais utilisé dans la pratique. Il est si rarement utilisé dans la vie réelle que l’installation de base de Jamovi n’a pas de fonction intégrée pour cela. Cependant, le test est si simple qu’il est très facile de le faire manuellement. Revenons aux données de la classe du Dr Zeppo. Après avoir chargé les données des notes, la première chose que je dois faire est de calculer la moyenne de l’échantillon, ce que j’ai déjà fait (72,3). Nous avons déjà la norme de population connue (\(\sigma = 9,5\)), et la valeur de la population signifie que l’hypothèse nulle spécifie (\(\mu_{0} = 67,5\)), et on connaît la taille de l’échantillon (N=20).

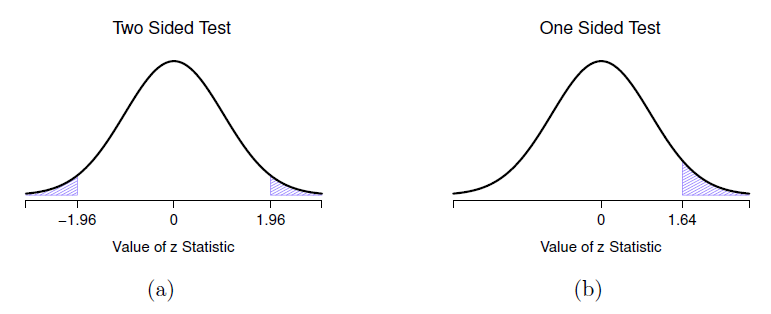
Figure 11‑3 : Régions de rejet pour le test z bilatéral (panneau a) et le test z unilatéral (panneau b).

Ensuite, calculons l’erreur type (vraie) de la moyenne (facile à faire avec une calculatrice) :

\[\begin{aligned} \text{sem.true} & =\text{sd.true}/\text{sqrt}\\ & =9,5/\text{sqrt}\\ &=2,124265 \end{aligned} \]

Et enfin, nous calculons notre z-score :

\[ \begin{aligned} \text{z.score} & =\left (\text{sample.mean}-\text{mu.null}\right )/\text{sem.true}\\ & = \left ( 72,3-67,5 \right )/2,124265\\ & = 2,259606 \end{aligned} \]

À ce stade, nous chercherions traditionnellement la valeur 2,26 dans notre tableau des valeurs critiques. Notre hypothèse initiale était bilatérale (nous n’avions pas vraiment de théorie expliquant pourquoi les étudiants en psychologie seraient meilleurs ou pires en statistiques que les autres étudiants), alors notre test d’hypothèse est bilatéral. En regardant le petit tableau que j’ai présenté plus tôt, on constate que 2,26 est supérieur à la valeur critique de 1,96 qui devrait être significative à \(\alpha=.05\), mais inférieure à la valeur de 2,58 qui devrait être significative à un niveau de \(\alpha=.01\). Par conséquent, nous pouvons conclure que nous avons un effet significatif, que nous pourrions écrire en disant quelque chose comme ceci :

Avec une note moyenne de 73,2 dans l’échantillon d’étudiants en psychologie, et en supposant un écart type de population réel de 9,5, nous pouvons conclure que les étudiants en psychologie ont des scores statistiques significativement différents de la moyenne de la classe (\(z=2,26, N=20, p<.05\)).

11.1.4 Hypothèses du z-test

Comme je l’ai déjà dit, tous les tests statistiques font des hypothèses. Certains tests font des hypothèses raisonnables, alors que d’autres ne le font pas. Le test que je viens de décrire, le test z-test à un échantillon, fait trois hypothèses de base. Celles-ci le sont :

• Normalité. Comme on le décrit habituellement, le test z suppose que la distribution réelle de la population est normale.⁸⁰ C’est souvent une hypothèse assez raisonnable, et c’est aussi une hypothèse que nous pouvons vérifier si nous nous en inquiétons (voir Section 11.8).

• Indépendance. La deuxième hypothèse du test est que les observations de votre ensemble de données ne sont pas corrélées entre elles, ou reliées entre elles. Ce n’est pas aussi facile à vérifier statistiquement, cela repose un peu sur un bon plan expérimental. Un exemple évident (et stupide) d’une situation qui viole cette hypothèse est un ensemble de données où vous « copiez » la même observation encore et encore dans votre fichier de données de sorte que vous obtenez une « taille d’échantillon » massive, qui consiste en une seule observation réelle. De façon plus réaliste, vous devez vous demander s’il est vraiment plausible d’imaginer que chaque observation est un échantillon complètement aléatoire de la population qui vous intéresse. Dans la pratique, cette hypothèse n’est jamais respectée, mais nous faisons de notre mieux pour concevoir des études qui minimisent les problèmes de corrélation des données.

• Écart-type connu. La troisième hypothèse du test z est que le chercheur connaît l’écart-type réel de la population. C’est juste stupide. Dans aucun problème réel d’analyse de données, vous connaissez l’écart-type \(\sigma\) de certaines populations, tout en ignorant complètement la moyenne \(\mu\). En d’autres termes, cette hypothèse est toujours fausse.

Compte tenu de la stupidité de supposer que \(\sigma\) est connu, voyons si nous pouvons nous en passer. Cela nous emmène hors du domaine morne du test z, et dans le royaume magique du test t, avec des licornes, des fées et des lutins !

11.2 Le test t sur un échantillon

Après mûre réflexion, j’ai décidé qu’il ne serait peut-être pas prudent de supposer que les notes des étudiants en psychologie ont nécessairement le même écart-type que les autres étudiants de la classe du Dr Zeppo. Après tout, si je fais l’hypothèse qu’ils n’ont pas la même moyenne, alors pourquoi devrais-je croire qu’ils ont absolument le même écart-type ? Compte tenu de cela, je devrais vraiment arrêter de supposer que je connais la vraie valeur de \(\sigma\). Cela viole les suppositions de mon test z, donc dans un sens, je suis de retour à la case départ. Cependant, ce n’est pas comme si j’étais complètement à court d’options. Après tout, j’ai toujours mes données brutes, et ces données brutes me donnent une estimation de l’écart-type de la population, qui est de 9,52. En d’autres termes, si je ne peux pas dire que je sais que \(\sigma = 9,5\), je peux dire que \(\hat{\sigma} = 9,52\).

Bien ! Une solution évidente à laquelle vous pourriez penser est d’effectuer un test z, mais en utilisant l’écart type estimé de 9,52 au lieu de vous fier à mon hypothèse de l’écart type réel de 9,5. Et vous ne seriez probablement pas surpris d’apprendre que cela nous donnerait quand même un résultat significatif. Cette solution est proche, mais elle n’est pas tout à fait correcte. Comme nous nous fions maintenant à une estimation de l’écart-type de la population, nous devons faire un certain ajustement pour tenir compte du fait que nous avons une certaine incertitude quant à la véritable valeur de l’écart-type de la population. Peut-être que nos données ne sont qu’un coup de chance… peut-être que l’écart-type réel de la population est de 11, par exemple. Mais si c’était vrai, et nous ayons réalisé le test z en supposant que \(\sigma=11\), alors le résultat serait non significatif. C’est un problème, et c’est un problème que nous allons devoir régler.

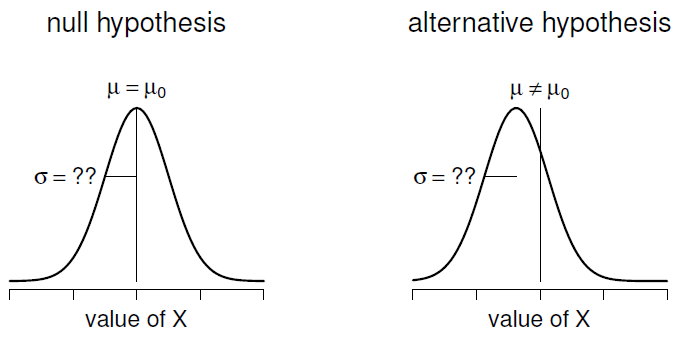
Figure 11‑4 : Illustration graphique de l’hypothèse nulle et de l’hypothèse alternative supposée par le test t pour un échantillon (bilatéral). Notez la similitude avec le test z (Figure 11‑2). L’hypothèse nulle est que la moyenne de population µ est égale à une valeur spécifiée \(\mu_{0}\), et l’hypothèse alternative est que ce n’est pas le cas. Comme pour le test z, nous supposons que les données sont normalement distribuées, mais nous ne supposons pas que l’écart type de population \(\sigma\) est connu à l’avance.

11.2.1 Présentation du test t-test

Cette ambiguïté est agaçante, et elle a été résolue en 1908 par un type appelé William Sealy Gosset (Student 1908), qui travaillait alors comme chimiste à la brasserie Guinness (voir (1987)). Parce que Guinness avait une mauvaise opinion de ses employés qui publiaient des analyses statistiques (apparemment ils pensaient que c’était un secret commercial), il a publié l’ouvrage sous le pseudonyme « A Student » et, à ce jour, le nom complet du t-test est en fait le test t de Student.

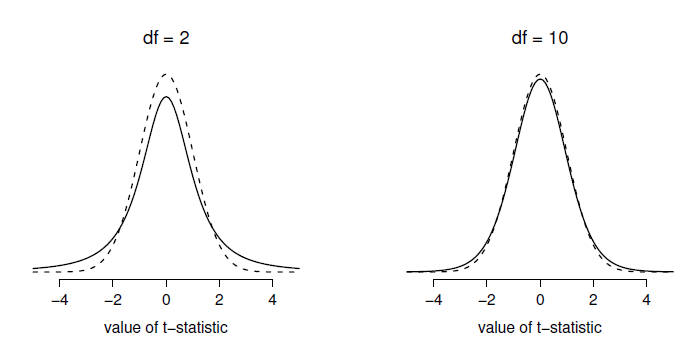
Figure 11‑5 : La distribution t avec 2 degrés de liberté (à gauche) et 10 degrés de liberté (à droite), avec une distribution normale standard (c.-à-d. moyenne 0 et écart-type 1) représentée par des lignes pointillées à des fins de comparaison. Notez que la distribution t a des queues plus importantes (leptocurtique : kurtosis plus élevé) que la distribution normale ; cet effet est assez exagéré lorsque les degrés de liberté sont très faibles, mais négligeable pour des valeurs plus grandes. En d’autres termes, pour un grand df, la distribution t est pratiquement identique à une distribution normale.

Ce que Gosset a compris, c’est qu’il faut tenir compte du fait que nous ne savons pas exactement quel est l’écart-type réel.⁸¹ La réponse est qu’il modifie subtilement la distribution d’échantillonnage. Dans le test t, notre statistique de test, maintenant appelée statistique t, est calculée exactement de la même manière que je l’ai exposé ci-dessus. Si notre hypothèse nulle est que la vraie moyenne est \(\mu\), mais que notre échantillon a une moyenne \(\bar{X}\) et que notre estimation de l’écart-type de la population est \(\hat{\sigma}\), alors notre statistique t est :

\[ t = \frac{\bar{X} - \mu}{\hat{\sigma}/\sqrt{N}} \]

La seule chose qui a changé dans l’équation est qu’au lieu d’utiliser la valeur réelle connue \(\sigma\), nous utilisons l’estimation \(\hat{\sigma}\). Et si cette estimation a été construite à partir de N observations, alors la distribution d’échantillonnage se transforme en une distribution t avec N - 1 degrés de liberté* (df). La distribution t est très semblable à la distribution normale, mais a des queues plus « importantes », comme on l’a vu plus haut à la section 7.6 et illustré à la Figure 11‑5. Notez, cependant, qu’à mesure que df s’agrandit, la distribution t tend à être identique à la distribution normale standard. C’est comme il se doit : si vous avez un échantillon de N = 70 000 000 000, alors votre « estimation » de l’écart-type devrait être à peu près parfaite. Il faut donc s’attendre à ce que pour un grand N, le t-test se comporte exactement de la même manière qu’un test z. Et c’est exactement ce qui se passe !

11.2.2 Faire le test avec Jamovi

Comme on peut s’y attendre, la mécanique du test t est presque identique à celle du test z. Il n’y a donc pas beaucoup d’intérêt à faire l’exercice fastidieux de vous montrer comment faire les calculs à l’aide de commandes de bas niveau. C’est à peu près identique aux calculs que nous avons faits plus tôt, sauf que nous utilisons l’écart-type estimé et que nous testons ensuite notre hypothèse en utilisant la distribution t plutôt que la distribution normale. Ainsi, au lieu de passer en revue les calculs en détail fastidieux pour une deuxième fois, je vais vous montrer comment les tests t sont réellement effectués. Jamovi est livré avec une analyse dédiée pour les tests t qui est très flexible (il peut exécuter de nombreux types de tests t différents). C’est assez simple à utiliser ; tout ce que vous avez à faire est de sélectionner « Analyses » - « T-Tests » - « One Sample T-Test », déplacer la variable qui vous intéresse (X) dans la case « Variables », et taper la valeur moyenne de l’hypothèse nulle « 67.5 » dans la case « Hypothesis » -« Test value ». C’est assez facile. Voir Figure 11‑6, qui, entre autres choses que nous allons aborder dans un instant, vous donne une statistique t-test = 2,25, avec 19 degrés de liberté et une valeur p associée de 0,036.

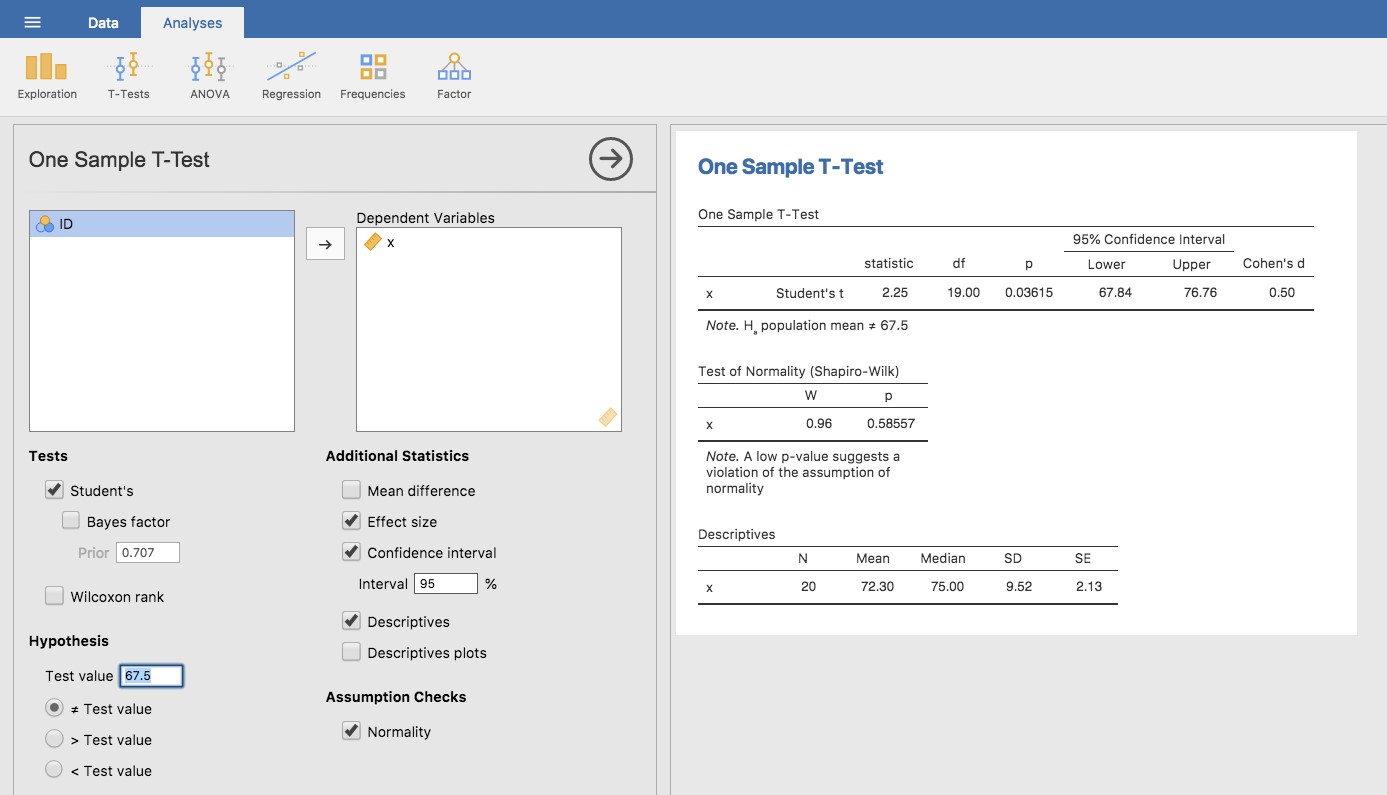
Figure 11‑6 : Jamovi effectue le test t sur un échantillon.

Il y a aussi deux autres choses qui pourraient vous intéresser : l’intervalle de confiance à 95 % et une mesure de la taille de l’effet (on en reparlera plus loin). Cela semble donc assez simple. Maintenant, que faisons-nous de cette sortie ? Eh bien, nous sommes ravis de découvrir que le résultat est statistiquement significatif (c’est-à-dire que la valeur p est inférieure à 0,05). Nous pourrions rapporter le résultat en disant quelque chose comme ceci :

Avec une note moyenne de 72,3, les étudiants en psychologie ont obtenu une note légèrement supérieure à la note moyenne de 67,5 (t(19)=2,25, p<.05); l’intervalle de confiance à 95 % est de 67,8 à 76.8.

où t(19) est une notation condensée pour une statistique t qui a 19 degrés de liberté. Cela dit, il arrive souvent que les gens ne signalent pas l’intervalle de confiance, ou qu’ils le fassent en utilisant une forme beaucoup plus comprimée que ce que j’ai fait ici. Par exemple, il n’est pas rare de voir l’intervalle de confiance inclus dans le bloc statistique, comme ceci :

\[t(19) =2,25, p<.05, C_{I95} = [67,8;76,8]\]

Avec tout ce jargon entassé dans une demi-ligne, vous savez qu’il doit être très intelligent.⁸²

11.2.3 Hypothèses d’un test t sur un échantillon

Bien, quelles sont les hypothèses du test t sur un échantillon ? Eh bien, puisque le test t est fondamentalement un test z sans l’hypothèse d’écart type connu, vous ne devriez pas être surpris de voir qu’il fait les mêmes hypothèses que le test z, moins celle de l’écart type connu. C’est-à-dire

• Normalité. Nous supposons toujours que la distribution de la population est normale⁸³ et, comme nous l’avons déjà mentionné, il existe des outils standards que vous pouvez utiliser pour vérifier si cette hypothèse est remplie (Section 11.8, et d’autres tests que vous pouvez faire à sa place si cette hypothèse est violée (Section 11.9).

• Indépendance. Encore une fois, nous devons supposer que les observations de notre échantillon sont générées indépendamment les unes des autres. Voir la discussion précédente sur le test z pour les spécificités (Section 11.1.4).

Dans l’ensemble, ces deux hypothèses ne sont pas très déraisonnables et, par conséquent, le test t pour un échantillon est assez largement utilisé dans la pratique pour comparer la moyenne d’un échantillon à une moyenne de population supposée.

11.3 Les tests de student pour échantillons indépendants

Bien que le test t-test pour un échantillon ait ses utilisations, ce n’est pas l’exemple le plus typique d’un test t⁸⁴. Une situation beaucoup plus courante survient lorsque vous avez deux groupes d’observations différents. En psychologie, cela tend à correspondre à deux groupes différents de participants, où chaque groupe correspond à une condition différente dans votre étude. Pour chaque personne participant à l’étude, vous mesurez une variable d’intérêt, et la question de recherche que vous posez est de savoir si les deux groupes ont ou non la même moyenne de population. C’est la situation pour laquelle le t-test des échantillons indépendants est conçu.

11.3.1 Les données

Supposons que 33 étudiants suivent les cours du Dr Harpo sur les statistiques, et que le Dr Harpo n’est pas noté selon une courbe. En fait, la notation du Dr Harpo est un peu mystérieuse, nous ne savons donc pas vraiment quelle est la note moyenne pour l’ensemble de la classe. Il y a deux tuteurs pour la classe, Anastasia et Bernadette. Il y a N₁=15 élèves dans les travaux dirigés d’Anastasia, et N₂=18 dans ceux de Bernadette. La question de recherche qui m’intéresse est de savoir si Anastasia ou Bernadette est une meilleure tutrice, ou si cela ne fait pas une grande différence. Le Dr Harpo m’a envoyé les notes de cours par e-mail, dans le fichier harpo.csv. Comme d’habitude, je vais charger le fichier dans Jamovi et regarder quelles variables il contient - il y a trois variables, ID, grade et tuteur. La variable de note contient la note de chaque élève, mais elle n’est pas importée dans Jamovi avec l’attribut de niveau de mesure correct, donc je dois la modifier pour qu’elle soit considérée comme une variable continue (voir section 3.6). La variable du tuteur est un facteur qui indique qui était le tuteur de chaque élève - soit Anastasia ou Bernadette.

Nous pouvons calculer les moyennes et les écarts-types à l’aide de l’analyse « Exploration » -« Descriptives », et voici un joli petit tableau récapitulatif :

	mean	std dev	N
Les élèves d’Anastasia	74,53	9,00	15
Les élèves de Bernadette	69,06	5,77	18

Pour vous donner une idée plus détaillée de ce qui se passe ici, j’ai tracé des histogrammes (non pas en Jamovi, mais en utilisant R) montrant la distribution des notes pour les deux tuteurs (Figure 11‑7), ainsi qu’un graphique plus simple montrant les moyennes et les intervalles de confiance correspondants des deux groupes d’élèves (Figure 11‑8).

11.3.2 Présentation du test

Le t-test d’échantillons indépendants se présente sous deux formes différentes, celle de Student et celle de Welch. Le t-test original de Student, qui est celui que je vais décrire dans cette section, est le plus simple des deux mais repose sur des hypothèses beaucoup plus restrictives que le test t de Welch.

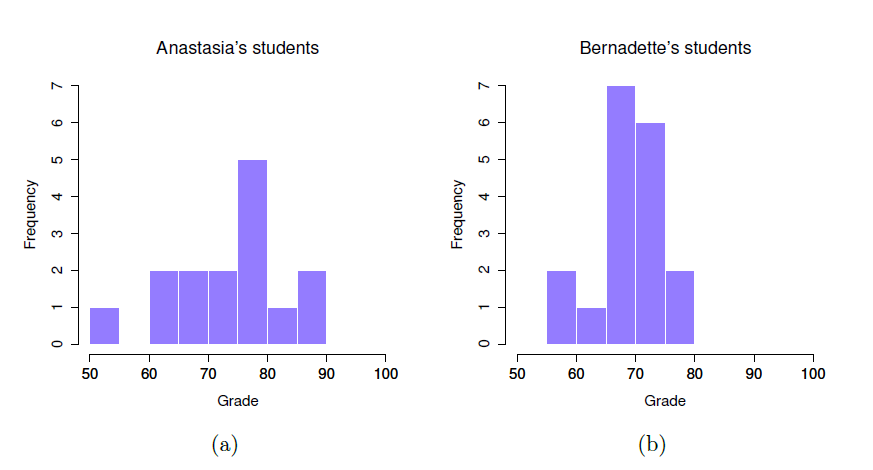
Figure 11‑7 : Histogrammes montrant la distribution des notes des élèves des classes d’Anastasia (figure a) et de Bernadette (figure b). Visuellement, cela suggère que les élèves de la classe d’Anastasia peuvent obtenir de meilleures notes en moyenne, bien qu’elles semblent aussi un peu plus dispersées.

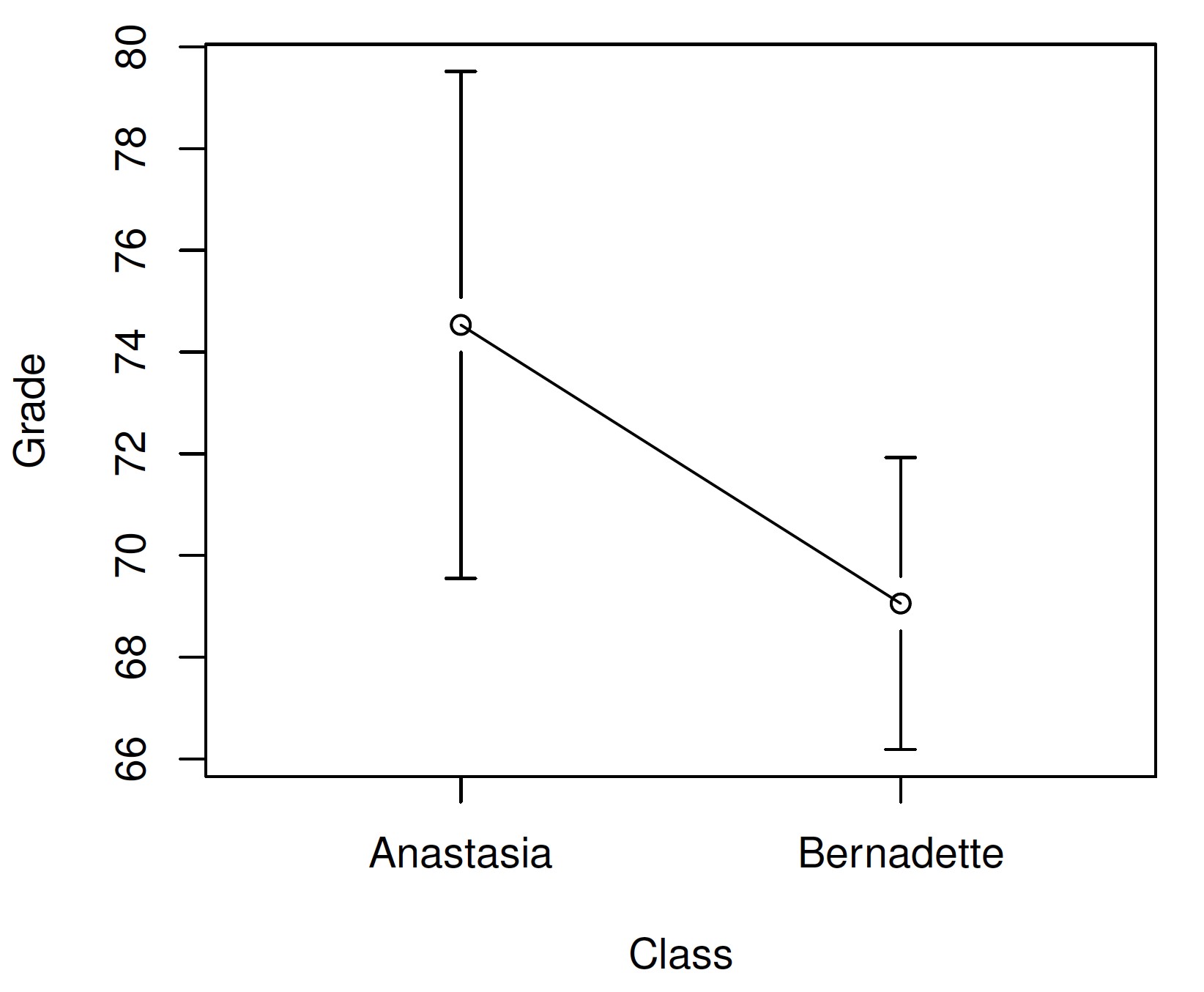
Figure 11‑8 : Le graphique illustre la note moyenne des élèves des travaux dirigées d’Anastasia et de Bernadette. Les barres d’erreur représentent des intervalles de confiance à 95 % autour de la moyenne. Visuellement, on dirait qu’il y a une vraie différence entre les groupes, mais c’est difficile à dire avec certitude.

En supposant pour l’instant que l’on veuille effectuer un test bilatéral, le but est de déterminer si deux « échantillons indépendants » de données sont tirés de populations ayant la même moyenne (l’hypothèse nulle) ou des moyennes différentes (l’hypothèse alternative). Lorsque nous parlons d’échantillons « indépendants », ce que nous voulons dire ici, c’est qu’il n’y a pas de relation particulière entre les observations des deux échantillons. Cela n’a probablement pas beaucoup de sens pour l’instant, mais ce sera plus clair lorsque nous parlerons des tests t pour échantillons appariés plus tard. Pour l’instant, signalons simplement que si nous avons un plan expérimental où les participants sont répartis au hasard dans l’un des deux groupes et que nous voulons comparer la performance moyenne des deux groupes en fonction d’une mesure des résultats, alors c’est un test t pour échantillons indépendants (plutôt qu’un test t apparié) qui nous intéresse.

Ok, donc posons \(\mu_{1}\) pour indiquer la vraie moyenne de population pour le groupe 1 (par exemple, les étudiants d’Anastasia), et \(\mu_{2}\) sera la vraie moyenne de population pour le groupe 2 (par exemple, les étudiants de Bernadette),⁸⁵ et comme d’habitude nous laissons \(\bar{X_{1}}\) et \(\bar{X_{2}}\) indiquer les moyennes observées pour ces deux groupes. Notre hypothèse nulle indique que les deux moyennes de population sont identiques (\(\mu_{1} = \mu_{2}\)) et l’alternative est qu’elles ne le sont pas (\(\mu_{1} \neq \mu_{2}\)). Voici cela écrit en termes mathématique :

\[\text{H}_{0}=\mu_{1} = \mu_{2})\\ \text{H}_{1}=\mu_{1} \neq \mu_{2})\]

Pour construire un test d’hypothèse qui traite ce scénario, nous commençons par noter que si l’hypothèse nulle est vraie, alors la différence entre les moyennes de population est exactement nulle, \(\mu_{1}-\mu_{2}=0\). Par conséquent, une statistique de test diagnostique sera basée sur la différence entre les deux moyennes de l’échantillon. Parce que si l’hypothèse nulle est vraie, on s’attendrait à ce que \(\bar{X_{1}}-\bar{X_{2}}\) soit assez proche de zéro. Cependant, tout comme nous l’avons vu avec nos tests sur un échantillon (c.-à-d. le test z sur un échantillon et le test t sur un échantillon), nous devons être précis quant à savoir exactement dans quelle mesure cette différence devrait être proche de zéro. Et la solution au problème est plus ou moins la même. Nous calculons une estimation de l’erreur-type (SE pour standard error), comme la dernière fois, puis nous divisons la différence entre les moyennes par cette estimation. Notre statistique T sera donc de la forme :

\[ t = \frac{{\bar{X}}_{1} - {\bar{X}}_{2}}{\text{SE}} \]

Nous avons juste besoin de savoir ce qu’est réellement cette estimation de l’erreur type. C’est un peu plus délicat que pour l’un ou l’autre des deux tests que nous avons examinés jusqu’à présent, et nous devons donc l’examiner beaucoup plus attentivement pour comprendre comment il fonctionne.

11.3.3 Une « estimation globale » de l’écart-type

Dans le « test t de Student t-test » original, nous partons du principe que les deux groupes ont le même l’écart-type de la population. C’est-à-dire que, peu importe si les moyennes de population sont les mêmes, nous supposons que les écarts-types de population sont identiques, \(\sigma_{1}=\sigma_{2}\), l’écart-type de la population.

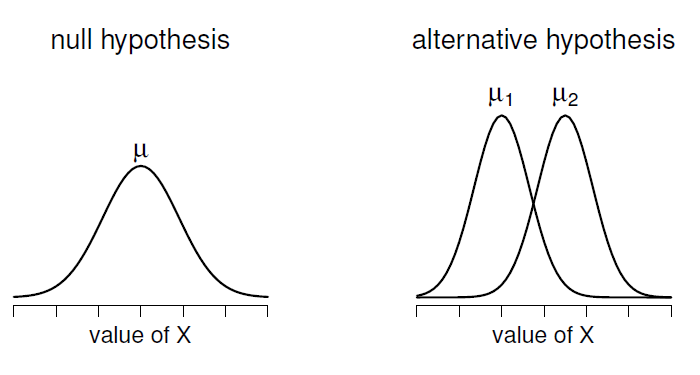
Figure 11‑9 : Illustration graphique des hypothèses nulle et alternative supposées par le test t de Student. L’hypothèse nulle suppose que les deux groupes ont la même moyenne \(\mu\), alors que l’hypothèse alternative suppose qu’ils ont des moyennes différentes \(\mu_{1}\) et \(\mu_{2}\). Notez qu’on suppose que les distributions de la population sont normales et que, bien que l’hypothèse alternative permette au groupe d’avoir des moyennes différentes, elle suppose qu’ils ont le même écart-type.

C’est-à-dire que, peu importe si les moyennes de population sont les mêmes, nous supposons que les écarts-types de population sont identiques, \(\sigma_{1}=\sigma_{2}\). Puisque nous supposons que les deux écarts-types sont les mêmes, nous supprimons les indices et les appelons tous les deux \(\sigma\). Comment devrions-nous les estimer ? Comment construire une estimation unique d’un écart-type lorsque nous avons deux échantillons ? La réponse est qu’en gros, nous en faisons la moyenne. Enfin, en quelque sorte. En fait, nous prenons une moyenne pondérée des estimations de la variance, que nous utilisons comme estimation globale de la variance. Le poids attribué à chaque échantillon est égal au nombre d’observations dans cet échantillon, moins 1.

Mathématiquement, nous pouvons écrire ceci comme suit

\[w_{1}=N_{1}-1\\ w_{2}=N_{2}-1\]

Maintenant que nous avons attribué des pondérations à chaque échantillon, nous calculons l’estimation globale de la variance en prenant la moyenne pondérée des deux estimations de variance, \({\hat{\sigma}}_{1}^{2}\) et \({\hat{\sigma}}_{2}^{2}\)

\[ {\hat{\sigma}}_{p}^{2} = \frac{{w_{1}\hat{\sigma}}_{1}^{2} + {w_{2}\hat{\sigma}}_{2}^{2}}{w_{1} + w_{2}} \]

Enfin, nous convertissons l’estimation de la variance globale en une estimation de l’écart-type regroupée, en prenant la racine carrée.

\[ {\hat{\sigma}}_{p}^{2} = \sqrt{\frac{{w_{1}\hat{\sigma}}_{1}^{2} + {w_{2}\hat{\sigma}}_{2}^{2}}{w_{1} + w_{2}}} \]

Et si vous remplacez mentalement \(w_{1} = N_{1}-1\) et \(w_{2} = N_{2}-1\) dans cette équation, vous obtenez une formule très moche. Une formule très moche qui semble en fait être la façon « standard » de décrire l’estimation de l’écart-type globale. Ce n’est toutefois pas ma façon préférée de voir les écarts-types globaux. Je préfère voir les choses comme ça. Notre ensemble de données correspond en fait à un ensemble de N observations qui sont classées en deux groupes. Utilisons donc la notation X_ik pour faire référence à la note reçue par le i-ème élève dans le k-ème groupe de tutorat. C’est-à-dire, X₁₁ est la note reçue par le premier élève de la classe d’Anastasia, X₂₁ est son deuxième élève, et ainsi de suite. Et nous avons deux moyennes de groupe séparées \({\bar{X}}_{1}\) et \({\bar{X}}_{2}\), que nous pourrions « génériquement » désigner en utilisant la notation \({\bar{X}}_{k}\), c’est-à-dire la note moyenne pour le k-ème groupe de tutorat. Pour l’instant, tout va bien. Maintenant, puisque chaque élève tombe dans l’un des deux travaux dirigés, nous pouvons décrire son écart par rapport à la moyenne du groupe comme étant la différence suivante

\[ {X_{{ik}} - \bar{X}}_{k} \]

Alors pourquoi ne pas simplement utiliser ces écarts (c.-à-d. la mesure dans laquelle la note de chaque élève diffère de la note moyenne dans son groupe de travaux dirigés) ? N’oubliez pas qu’une variance n’est que la moyenne d’un ensemble d’écarts quadratiques, alors faisons-le. Mathématiquement, nous pourrions l’écrire comme ceci

\[ \frac{\sum_{{ik}}^{}\left( X_{{ik}} - \bar{X_{k}} \right)^{2}}{N} \]

où la notation \(\sum_{{ik}}\) est une façon paresseuse de dire « calculer une somme en regardant tous les élèves dans tous les travaux dirigés», puisque chaque « ik » correspond à un élève⁸⁶. Mais, comme nous l’avons vu au chapitre 8, calculer la variance en divisant par N produit une estimation biaisée de la variance de la population. Et auparavant, nous devions diviser par N - 1 pour résoudre ce problème. Toutefois, comme je l’ai mentionné à l’époque, la raison pour laquelle ce biais existe est que l’estimation de la variance repose sur la moyenne de l’échantillon, et dans la mesure où la moyenne de l’échantillon n’est pas égale à celle de la population, elle peut systématiquement biaiser notre estimation de la variance. Mais cette fois, nous comptons sur deux moyennes d’échantillons ! Est-ce que cela signifie que nous avons plus de biais ? Oui, c’est vrai. Et cela signifie-t-il que nous devons maintenant diviser par N - 2 au lieu de N - 1, afin de calculer notre estimation de la variance globale ? Oui, bien sûr.

\[ {\hat{\sigma}}_{p}^{2} = \frac{\sum_{{ik}}^{}\left( X_{{ik}} - \bar{X_{k}} \right)^{2}}{N - 2} \]

Si vous prenez la racine carrée de ceci alors vous obtenez \({\hat{\sigma}}_{p}\), l’estimation de l’écart-type global. En somme, le calcul de l’écart-type global n’a rien de particulier. Ce n’est pas très différent du calcul normal de l’écart-type.

11.3.4 Terminer le test

Quelle que soit la façon dont vous voulez y penser, nous avons maintenant notre estimation globale de l’écart-type. A partir de maintenant, je vais laisser tomber le stupide indice p, et me référer simplement à cette estimation en tant que \(\hat{\sigma}\). Super ! Revenons maintenant au test de l’hypothèse de départ, d’accord ? La raison pour laquelle nous avons calculé cette estimation est que nous savions qu’elle serait utile pour calculer notre estimation de l’erreur-type. Mais l’erreur type de quoi ? Dans le test t sur un échantillon c’était l’erreur-type de la moyenne de l’échantillon, \({SE}\left(\bar{X} \right)\), et alors \({SE}\left(\bar{X} \right) = {\sigma}/\sqrt{{N}}\) c’est ce à quoi ressemblait le dénominateur de notre statistique t. Cette fois-ci, cependant, nous avons deux moyennes d’échantillon. Et ce qui nous intéresse, en particulier, c’est la différence entre les deux \({\bar{X}}_{1} - {\bar{X}}_{2}\) Par conséquent, l’erreur-type par laquelle nous devons diviser est en fait l’erreur-type de la différence entre les moyennes.

Tant que les deux variables ont réellement le même écart-type, notre estimation de l’erreur type est la suivante :

\[ \text{SE}\left( {\bar{X}}_{1} - {\bar{X}}_{2} \right) = \hat{\sigma}\sqrt{\frac{1}{N_{1}} + \frac{1}{N_{2}}} \]

et notre statistique t est donc

\[ t = \frac{{\bar{X}}_{1} - {\bar{X}}_{2}}{\text{SE}\left( {\bar{X}}_{1} - {\bar{X}}_{2} \right)} \]

Comme nous l’avons vu avec notre test sur un échantillon, la distribution d’échantillonnage de cette statistique t est une distribution t (surprenant, non ?) tant que l’hypothèse nulle est vraie et que tous les présupposés du test sont remplis. Les degrés de liberté, cependant, sont légèrement différents. Comme d’habitude, on peut penser aux degrés de liberté pour être égal au nombre de points de données moins le nombre de contraintes. Dans ce cas, nous avons N observations (N₁ dans l’échantillon 1, et N₂ dans l’échantillon 2), et 2 contraintes (les moyennes des échantillons). Les degrés de liberté totaux pour ce test sont donc N-2.

11.3.5 Faire le test avec Jamovi

Vous ne serez pas surpris d’apprendre que vous pouvez faire un t-test d’échantillons indépendants facilement dans Jamovi. La variable résultat de notre test est la note de l’étudiant, et les groupes sont définis en fonction du tuteur pour chaque classe. Ainsi, vous ne serez probablement pas trop surpris que tout ce que vous avez à faire dans Jamovi est d’aller à l’analyse pertinente (« Analyses » - « T-Tests » -« Independent Samples T-Test ») et de déplacer la variable de note vers la case « Dependent Variables », et la variable tuteur vers la case « Grouping Variable », comme indiqué dans la Figure 11‑10.

Le résultat a une forme très familière. Tout d’abord, il vous indique quel test a été exécuté et le nom de la variable dépendante que vous avez utilisée. Il communique ensuite les résultats des tests. Comme la dernière fois, les résultats du test sont constitués d’une statistique t, des degrés de liberté et de la valeur p. La dernière section rapporte deux choses : elle vous donne un intervalle de confiance et une taille d’effet. Je parlerai de la taille de l’effet plus tard. L’intervalle de confiance, cependant, je devrais en parler maintenant.

Il est très important d’être clair sur ce à quoi se réfère cet intervalle de confiance. C’est un intervalle de confiance pour la différence entre les moyennes des groupes. Dans notre exemple, les élèves d’Anastasia avaient une note moyenne de 74,53 et les élèves de Bernadette avaient une note moyenne de 69,06, de sorte que la différence entre les deux moyennes de l’échantillon est de 5,48.

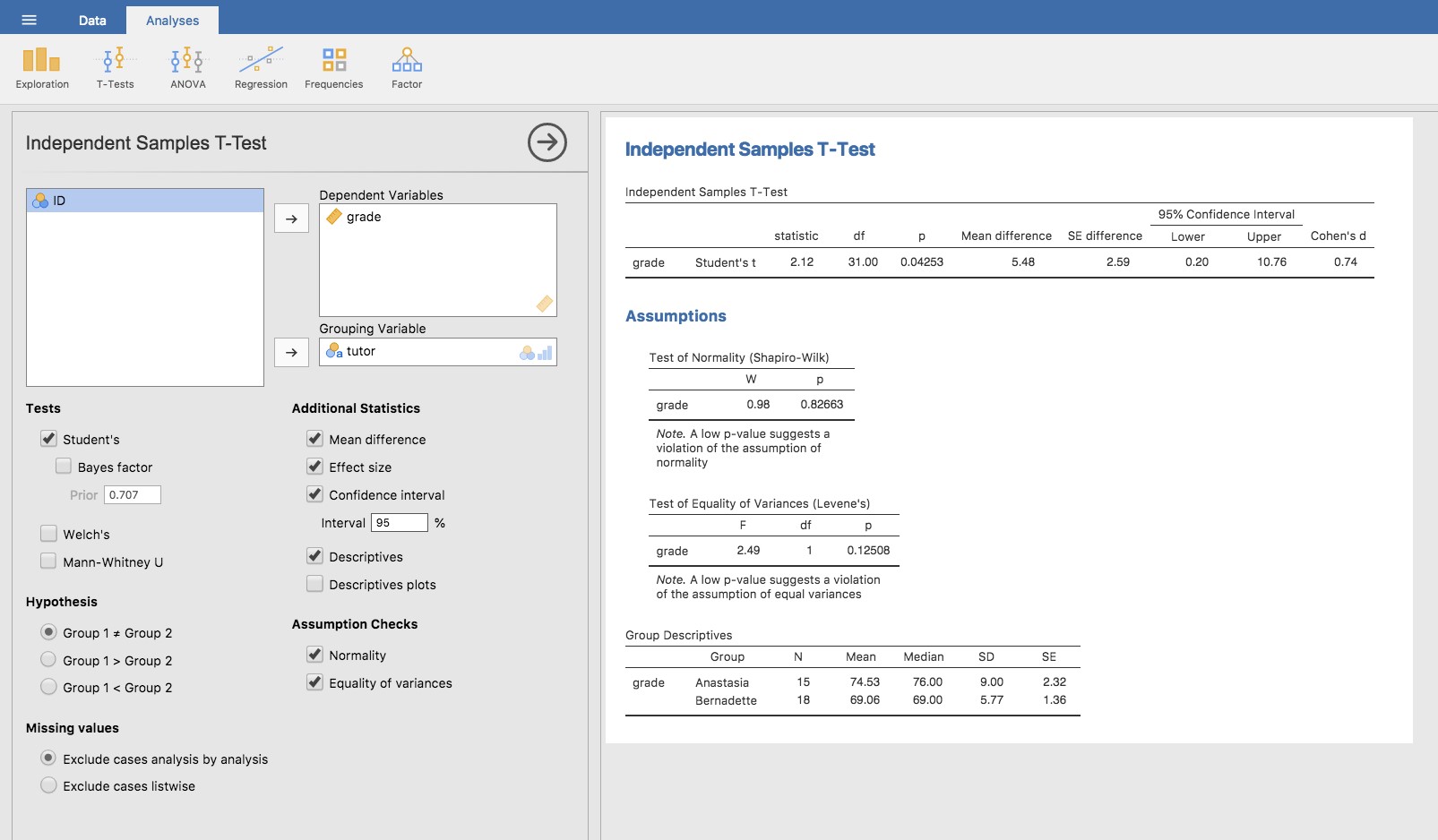
Figure 11‑10 : Test t indépendant dans Jamovi, avec les options utiles aux résultats cochées.

Bien sûr, la différence entre les moyennes de population peut être plus grande ou plus petite que cela. L’intervalle de confiance indiqué à la Figure 11‑10 vous indique que si nous répétons cette étude encore et encore, dans 95 % des cas, la vraie différence dans les moyennes se situe entre 0,20 et 10,76. Reportez-vous à la section 8.5 pour un rappel sur la signification des intervalles de confiance.

Dans tous les cas, la différence entre les deux groupes est significative (à peine), nous pourrions donc écrire le résultat en utilisant un texte comme celui-ci :

La note moyenne dans la classe d’Anastasia était de 74,5 (écart-type = 9,0), tandis que la moyenne dans la classe de Bernadette était de 69,1 (écart-type = 5,8). Le test t de Student sur des échantillons indépendants a montré que cette différence de 5,4% était significative \((t(31)=2,1, p<.05, CI_{95}=[0,2; 10,8], d=0,74)\), ce qui suggère qu’une différence réelle dans les résultats d’apprentissage a eu lieu.

Notez que j’ai inclus l’intervalle de confiance et la taille de l’effet dans le bloc de statistiques. Les auteurs ne font pas toujours ça. Au minimum, on s’attendrait à voir la statistique t, les degrés de liberté et la valeur p. Vous devriez donc inclure quelque chose comme ceci au minimum : \(t(31)=2,1, p<.05\). Si les statisticiens avaient leur mot à dire, tout le monde déclarerait aussi l’intervalle de confiance et probablement aussi la mesure de l’ampleur de l’effet, parce que ce sont des choses utiles à savoir. Mais la vraie vie ne fonctionne pas toujours de la façon dont les statisticiens le veulent, alors vous devrez faire un choix selon que vous pensez que cela aidera ou non vos lecteurs et, si vous rédigez un article scientifique, selon la norme éditoriale de la revue en question. Certains journaux s’attendent à ce que vous déclariez la taille de l’effet, d’autres non. Dans certaines communautés scientifiques, il est d’usage de signaler les intervalles de confiance, dans d’autres, ce n’est pas le cas. Vous devrez déterminer ce à quoi votre public s’attend. Mais, par souci de clarté, si vous prenez mon cours, ma position par défaut est qu’il vaut habituellement la peine d’inclure à la fois la taille de l’effet et l’intervalle de confiance.

11.3.6 Valeurs t positives et négatives

Avant de passer aux hypothèses du test t, j’aimerais faire une remarque supplémentaire sur l’utilisation des tests t dans la pratique. La première concerne le signe de la statistique t (c’est-à-dire s’il s’agit d’un nombre positif ou négatif). L’une des préoccupations les plus fréquentes des étudiants lorsqu’ils commencent à exécuter leur premier test t est qu’ils se retrouvent souvent avec des valeurs négatives pour la statistique t et qu’ils ne savent pas comment l’interpréter. En fait, il n’est pas rare que deux personnes travaillant indépendamment obtiennent des résultats presque identiques, sauf qu’une personne a une valeur t négative et l’autre une valeur t positive. En supposant que vous effectuez un test bilatéral, les valeurs p seront identiques. En y regardant de plus près, les étudiants remarqueront que les intervalles de confiance ont aussi les signes opposés. C’est tout à fait normal. Lorsque cela se produit, vous constaterez que les deux versions des résultats proviennent de deux façons légèrement différentes d’exécuter le t-test. Ce qui se passe ici est très simple. La statistique t que nous calculons ici est toujours de la forme

\[ t = \frac{(\text{moyenne1} - \text{moyenne2})}{\text{SE}} \]

Si « moyenne 1 » est supérieur à « moyenne 2 », la statistique t sera positive, alors que si « moyenne 2 » est supérieure, la statistique t sera négative. De même, l’intervalle de confiance que rapporte Jamovi est l’intervalle de confiance pour la différence « (moyenne 1) - (moyenne 2) », qui sera l’inverse de ce que vous obtiendriez si vous calculiez l’intervalle de confiance pour la différence « (moyenne 2) - (moyenne 1) ».

Bien, c’est assez simple quand on y pense, mais maintenant considérons notre t-test comparant la classe d’Anastasia à celle de Bernadette. Lequel devons-nous appeler « moyenne 1 » et lequel devons-nous appeler « moyenne 2 ». C’est arbitraire. Cependant, vous devez vraiment désigner l’un d’eux comme « moyenne 1 » et l’autre comme « moyenne 2 ». Il n’est pas surprenant que la façon dont Jamovi gère cela soit aussi assez arbitraire. Dans les versions antérieures du livre, j’essayais de l’expliquer, mais au bout d’un moment, j’ai abandonné, parce que ce n’est pas vraiment important et pour être honnête, je ne m’en souviens jamais moi-même. Chaque fois que j’obtiens un résultat significatif à un test t, et que je veux savoir quelle moyenne est la plus grande, je n’essaie pas de le déterminer en regardant la statistique t. Pourquoi je ferais ça ? C’est stupide. Il est plus facile de regarder simplement les moyennes réelles des groupes puisque la sortie Jamovi les montre !

Voilà le plus important. Parce que peu importe ce que Jamovi vous montre, j’essaie généralement de rapporter les statistiques t de manière à ce que les chiffres correspondent au texte. Supposons que ce que je veux écrire dans mon rapport est « La classe d’Anastasia avait des notes plus élevées que celle de Bernadette ». La formulation ici implique que le groupe d’Anastasia vient en premier, il est donc logique de rapporter la statistique t comme si la classe d’Anastasia correspondait au groupe 1. Si oui, j’écrirais que la classe d’Anastasia avait des notes supérieures à celle de Bernadette \(t(31) = 2,1, p =. 05\).

(Je ne soulignerais pas le mot « supérieur » dans la vie réelle, je le fais juste pour souligner le fait que « supérieur » correspond à des valeurs t positives). D’un autre côté, supposons que le commentaire que je voulais utiliser soit celui de la classe de Bernadette en premier. Si c’est le cas, il est plus logique de traiter sa classe comme un groupe 1, et si c’est le cas, l’écriture ressemble à ceci

La classe de Bernadette avait des notes plus faibles que celle d’Anastasia (\(t(31) = -2,1, p<. 05\)).

Parce que je parle d’un groupe ayant des scores « inférieurs » cette fois-ci, il est plus raisonnable d’utiliser la forme négative de la statistique t. C’est juste une écriture plus propre.

Une dernière chose : veuillez noter que vous ne pouvez pas faire cela pour d’autres types de statistiques de test. Il fonctionne pour les tests t, mais il ne serait pas possible pour les tests de chi-carré, les tests F ou même pour la plupart des tests dont je parle dans ce livre. Ne généralisez donc pas trop ce conseil ! Je ne parle que de tests t et de rien d’autre !

11.3.7 Hypothèses du test

Comme toujours, notre test d’hypothèse repose sur certaines hypothèses. Alors qu’elles sont-elles ? Pour le test t de Student, il y a trois hypothèses, dont certaines que nous avons vues précédemment dans le contexte du test t sur un échantillon (voir section 11.2.3) :

• Normalité. Comme pour le test t sur un échantillon, on suppose que les données sont normalement distribuées. Plus précisément, nous supposons que les deux groupes sont normalement distribués. Dans la section 11.8, nous discuterons de la façon de tester la normalité, et dans la section 11.9, nous discuterons des solutions possibles.

• Indépendance. Encore une fois, on suppose que les observations sont échantillonnées de façon indépendante. Dans le contexte du test de Student, cela comporte deux aspects. Premièrement, nous supposons que les observations à l’intérieur de chaque échantillon sont indépendantes les unes des autres (exactement de la même façon que pour le test sur un échantillon). Toutefois, nous supposons également qu’il n’y a pas de dépendances inter échantillons. Si, par exemple, il s’avère que vous avez inclus certains participants dans les deux conditions expérimentales de votre étude (par exemple, en permettant accidentellement à la même personne de s’inscrire à des conditions différentes), alors il y a des dépendances croisées d’échantillon que vous devrez prendre en compte.

• Homogénéité de la variance (aussi appelée « homoscédasticité »). La troisième hypothèse est que l’écart-type de la population est le même dans les deux groupes. Vous pouvez tester cette hypothèse en utilisant le test de Levene, dont je parlerai plus loin dans le livre (Section 13.6.1). Cependant, il y a un remède très simple à cette hypothèse si vous êtes inquiet, dont je parlerai dans la prochaine section.

11.4 Le test t des échantillons indépendants (test de Welch)

Le plus gros problème que pose l’utilisation du test de Student dans la pratique est la troisième hypothèse énoncée dans la section précédente. Il suppose que les deux groupes ont le même écart-type. C’est rarement vrai dans la vraie vie.

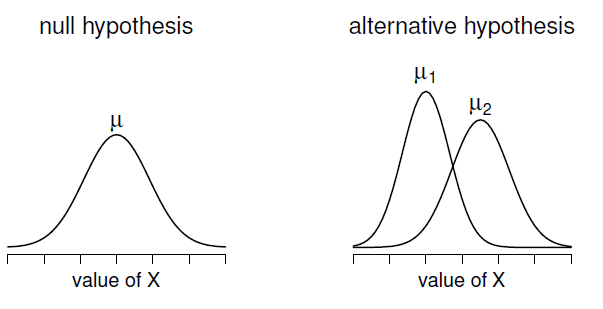
Figure 11‑11 : Illustration graphique des hypothèses nulles et alternatives supposées par le test t de Welch. Comme pour le test de Student (Figure 11‑9), nous supposons que les deux échantillons sont tirés d’une population normale, mais l’hypothèse alternative n’exige plus que les deux populations aient la même variance.

Si deux échantillons n’ont pas les mêmes moyennes, pourquoi devrions-nous nous attendre à ce qu’ils aient le même écart-type ? Il n’y a vraiment aucune raison de s’attendre à ce que cette hypothèse soit vraie. Nous parlerons un peu de la façon dont vous pourrez vérifier cette hypothèse plus tard parce qu’elle apparaît à différents endroits, et pas seulement au test t. Mais pour l’instant, je vais parler d’une autre forme de test t (Welch 1947) qui ne repose pas sur cette hypothèse. Une illustration graphique de ce que le test t de Welch suppose au sujet des données est présentée à la Figure 11‑11, afin de fournir un contraste avec la version du test de Student à la Figure 11‑9. J’admets qu’il est un peu étrange de parler du remède avant de parler du diagnostic, mais il se trouve que le test de Welch peut être spécifié comme l’une des options du « Independent Samples T-Test » dans Jamovi, c’est donc probablement le meilleur endroit pour en parler.

Le test de Welch est très semblable au test de Student. Par exemple, la statistique t que nous utilisons dans le test de Welch est calculée de la même façon que pour le test de Student. C’est-à-dire que nous prenons la différence entre les moyennes de l’échantillon et la divisons ensuite par une estimation de l’erreur type de cette différence.

\[ t = \frac{{\bar{X}}_{1} - {\bar{X}}_{2}}{\text{SE}\left( {\bar{X}}_{1} - {\bar{X}}_{2} \right)} \]

La principale différence est que les calculs de l’erreur type sont différents. Si les deux populations ont des écarts-types différents, il est complètement absurde d’essayer de calculer une estimation de l’écart type global, parce ce serait faire la moyenne de pommes et d’oranges.[Je suppose que vous pouvez faire la moyenne de pommes et d’oranges, et ce que vous obtenez est un délicieux smoothie aux fruits. Mais personne ne pense vraiment qu’un smoothie aux fruits est une très bonne façon de décrire les fruits originaux, non ?]

Mais vous pouvez toujours estimer l’erreur-type de la différence entre les moyennes de l’échantillon, elle finit par sembler différente.

\[ \text{SE}\left( {\bar{X}}_{1} - {\bar{X}}_{2} \right) = \sqrt{\frac{{\hat{\sigma}}_{1}^{2}}{N_{1}} + \frac{{\hat{\sigma}}_{1}^{2}}{N_{2}}} \]

La raison pour laquelle il est calculé de cette façon est au-delà de la portée de ce livre. Ce qui compte pour nous, c’est que la statistique t qui sort du test t de Welch soit en fait quelque peu différente de celle qui sort du test t de Student.

La deuxième différence entre Welch et Student est que les degrés de liberté sont calculés d’une manière très différente. Dans le test de Welch, les « degrés de liberté » n’ont plus besoin d’être un nombre entier, et ils ne correspondent plus du tout à règle du « nombre de points de données moins le nombre de contraintes » que j’ai utilisée jusqu’à présent.

Les degrés de liberté sont en fait

\[ ddl=\frac{\left (\hat{\sigma }^2_{1}/N_{1} + \hat{\sigma }^2_{2}/N_{2} \right )^{2}}{\left (\hat{\sigma}^{2}_{1}/N_{1} \right )^{2}/\left (N_{1}-1 \right )+\left (\hat{\sigma}^{2}_{1}/N_{1} \right)^2/\left ( N_{2}-1\right)} \] Ce qui est assez simple et évident, non ? Peut-être pas ! Ça n’a pas vraiment d’importance pour nous. Ce qui compte, c’est que vous verrez que la valeur « df » qui résulte d’un test de Welch a tendance à être un peu plus petite que celle utilisée pour le test de Student, et il n’est pas nécessaire que ce soit un nombre entier

11.4.1 Faire le test de Welch avec Jamovi

Si vous cochez la case pour le test de Welch dans l’analyse que nous avons faite ci-dessus, alors voici ce qu’il vous donne (Figure 11‑12) :

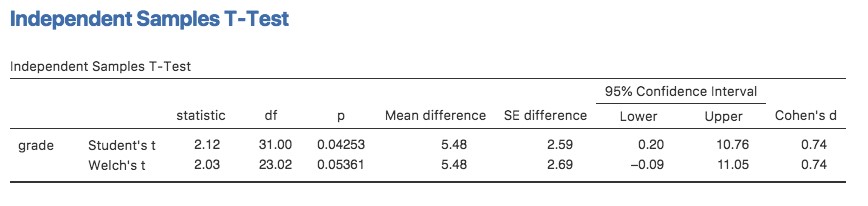
Figure 11‑12 : Résultats montrant le test Welch parallèlement au test t de Student par défaut dans Jamovi

L’interprétation de ce résultat devrait être assez évidente. Vous lirez le résultat du test de Welch de la même manière que vous le feriez pour le test de Student. Vous avez vos statistiques descriptives, les résultats des tests et d’autres informations. C’est donc assez facile.

Sauf que, sauf que… notre résultat n’est plus significatif. Lorsque nous avons effectué le test de Student, nous avons obtenu un effet significatif, mais le test de Welch sur le même ensemble de données ne l’est pas (\(t(23.02) = 2,03, p = .054)\). Qu’est-ce que cela signifie ? Devrions-nous paniquer ? Le ciel brûle-t-il ? Probablement pas. Le fait qu’un test soit significatif et l’autre ne le soit pas ne signifie pas grand-chose en soi, d’autant plus que j’ai en quelque sorte truqué les données pour que cela arrive. En règle générale, ce n’est pas une bonne idée d’essayer d’interpréter ou d’expliquer la différence entre une valeur p de .049 et une valeur p de.051. Si ce genre de chose se produit dans la vie réelle, la différence dans ces valeurs p est presque certainement due au hasard. Ce qui importe, c’est que vous preniez un peu de soin à réfléchir au test que vous utilisez. Le test de Student et le test de Welch ont des forces et des faiblesses différentes. Si les deux populations ont réellement des variances égales, alors le test de Student est légèrement plus puissant (taux d’erreur de type II inférieur) que le test de Welch. Cependant, s’ils n’ont pas les mêmes variances, alors les hypothèses du test de Student sont violées et vous pourriez ne pas être en mesure de lui faire confiance ; vous pourriez vous retrouver avec un taux d’erreur de Type I plus élevé. C’est donc un compromis. Cependant, dans la vie réelle, j’ai tendance à préférer le test de Welch, parce que presque personne ne croit vraiment que les écarts-types de population sont identiques.

11.4.2 Hypothèses du test

Les hypothèses du test de Welch sont très semblables à celles du test t de Student (voir la section 11.3.7), sauf que le test de Welch ne suppose pas d’homogénéité de la variance. Cela ne laisse que l’hypothèse de normalité et l’hypothèse d’indépendance. Les particularités de ces hypothèses sont les mêmes pour le test de Welch que pour le test de Student.

11.5 Le test t-test des échantillons appariés

Qu’il s’agisse du test de Student ou du test de Welch, un test t pour groupes indépendants est destiné à être utilisé dans une situation où vous avez deux échantillons qui sont indépendants l’un de l’autre. Cette situation se produit naturellement lorsque les participants sont assignés au hasard à l’une des deux conditions expérimentales, mais elle fournit une très mauvaise approximation par rapport à d’autres types de modèles de recherche. En particulier, l’analyse à l’aide de tests t pour échantillons indépendants ne convient pas un plan à mesures répétées, dans lequel chaque participant est mesuré (par rapport à la même variable de résultat) dans les deux conditions expérimentales. Par exemple, nous pourrions nous demander si l’écoute de musique réduit la capacité de mémoire de travail des gens. Pour ce faire, nous avons pu mesurer la capacité de mémoire de travail de chaque personne dans deux conditions : avec et sans musique. Dans un plan expérimental comme celui-ci,[Cette conception est très semblable à celle de la section 11.7 qui a motivé le test McNemar. Cela ne devrait pas être une surprise. Dans les deux cas, il s’agit de mesures répétées standard comportant deux mesures. La seule différence est que cette fois-ci, notre variable de résultat est une échelle d’intervalle (capacité de la mémoire de travail) plutôt qu’une variable d’échelle nominale binaire (une question oui ou non).] chaque participant apparaît dans les deux groupes. Cela nous oblige à aborder le problème d’une manière différente, en utilisant le test t pour des échantillons appariés.

11.5.1 Les données

Les données que nous utiliserons cette fois-ci proviennent de la classe du Dr Chico.⁸⁷ Dans sa classe, les élèves passent deux tests majeurs, l’un au début du semestre et l’autre plus tard dans le semestre. A l’entendre, elle dirige un cours très dure, un cours que la plupart des élèves trouvent très difficile. Mais elle soutient qu’en établissant des évaluations rigoureuses, on encourage les élèves à travailler plus fort. Sa théorie est que le premier test est une sorte de « réveil » pour les élèves. Quand ils réaliseront à quel point son cours est vraiment difficile, ils travailleront plus dur pour le deuxième test et obtiendront une meilleure note. A-t-elle raison ? Pour tester cela, importons le fichier chico.csv dans Jamovi. Cette fois, Jamovi fait un bon travail lors de l’importation de l’attribution correcte des échelles de mesure. L’ensemble de données chico contient trois variables : une variable id qui identifie chaque élève de la classe, la variable grade_test1 qui enregistre la note de l’élève pour le premier test, et la variable grade_test2 qui a les notes pour le second test.

Si nous regardons la feuille de calcul Jamovi, il semble que la classe est difficile (la plupart des notes se situent entre 50% et 60%), mais il semble y avoir une amélioration entre le premier et le second test.

Si nous examinons rapidement les statistiques descriptives de la Figure 11‑13, nous constatons que cette impression semble se confirmer. Pour l’ensemble des 20 élèves, la note moyenne pour le premier test est de 57, mais elle passe à 58 pour le deuxième test. Bien que les écarts-types soient respectivement de 6,6 et 6,4, il commence à sembler que l’amélioration n’est peut-être qu’illusoire ; peut-être une variation aléatoire. Cette impression est renforcée lorsque vous voyez les moyennes et les intervalles de confiance représentés à la Figure 11‑14a. Si nous devions nous fier uniquement à ce graphique et examiner l’ampleur de ces intervalles de confiance, nous serions tentés de croire que l’amélioration apparente du rendement des élèves est le fruit du hasard.

Néanmoins, cette impression est fausse. Pour comprendre pourquoi, jetez un coup d’œil au nuage de points des notes de l’épreuve 1 par rapport à celles de l’épreuve 2, comme le montre la Figure 11‑14b. Dans ce graphique, chaque point correspond aux deux notes d’un élève donné. Si leur note au test 1 (coordonnée x) est égale à leur note au test 2 (coordonnée y), le point tombe sur la ligne. Les points qui tombent au-dessus de la ligne sont les élèves qui ont obtenu de meilleurs résultats au deuxième test. De façon critique, presque tous les points de données se situent au-dessus de la ligne diagonale : presque tous les élèves semblent avoir amélioré leur note, ne serait-ce que d’une petite quantité. Cela suggère que nous devrions examiner les améliorations apportées par chaque élève d’un test à l’autre et considérer cela comme nos données brutes. Pour ce faire, nous devrons créer une nouvelle variable pour l’amélioration apportée par chaque élève, et l’ajouter à l’ensemble de données chico. La façon la plus simple de le faire est de calculer une nouvelle variable, avec l’expression grade test2 – grade test1

Une fois que nous avons calculé cette nouvelle variable d’amélioration, nous pouvons dessiner un histogramme montrant la distribution de ces scores d’amélioration, comme le montre la Figure 11‑14c. Quand on regarde l’histogramme, il est très clair qu’il y a une réelle amélioration. La grande majorité des élèves ont obtenu de meilleurs résultats au test 2 qu’au test 1, ce qui se reflète dans le fait que presque tout l’histogramme est au-dessus de zéro.

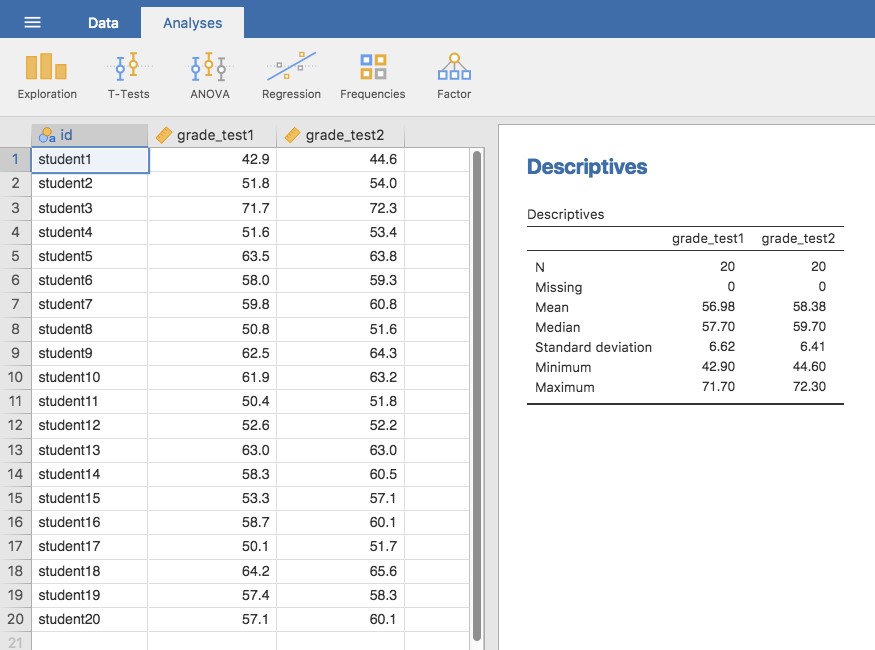
Figure 11‑13 : Analyse descriptives des deux variables d’essai de niveau dans l’ensemble de données de chico

11.5.2 Qu’est-ce que le test t-test des échantillons appariés ?

A la lumière de l’exploration précédente, réfléchissons à la manière de construire un test t approprié. Une possibilité serait d’essayer d’exécuter un test t d’échantillons indépendants en utilisant les variables grade_test1 et grade_test2 comme variables d’intérêt. Cependant, c’est clairement la mauvaise chose à faire car le test t des échantillons indépendants suppose qu’il n’y a pas de relation particulière entre les deux échantillons. Pourtant, il est clair que ce n’est pas vrai dans ce cas-ci en raison de la structure des mesures répétées dans les données. Pour reprendre le langage que j’ai présenté dans la dernière section, si nous essayions de faire un test t d’échantillons indépendants, nous confondrions les différences à l’intérieur du sujet (ce que nous voulons tester) avec la variabilité entre sujets (ce que nous ne faisons pas).

La solution au problème est évidente, je l’espère, puisque nous avons déjà fait tout le travail difficile dans la section précédente. Au lieu d’exécuter un test t d’échantillons indépendants sur grade_test1 et grade_test2, nous exécutons un test t sur un échantillon sur la variable de différence intra-sujet, l’amélioration. Pour formaliser un peu, si X_i1 est le score que le i-ème participant a obtenu sur la première variable, et X_i2 est le score que la même personne a obtenu sur la seconde, alors le score de différence est :

\[D_{i} = X_{i1} – X_{i2}\]

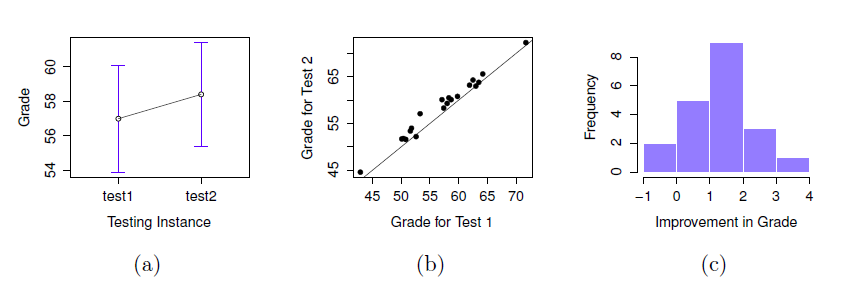
Figure 11‑14 : Note moyenne pour l’essai 1 et l’essai 2, avec des intervalles de confiance associés à 95 % (panel a). Diagramme de dispersion montrant les notes individuelles pour l’essai 1 et l’essai 2 (panneau b). Histogramme montrant l’amélioration réalisée par chaque élève de la classe du Dr Chico (panel c). Dans le panneau c, remarquez que la distribution est presque entièrement au-dessus de zéro : la grande majorité des élèves ont amélioré leur performance du premier au deuxième test.

Notez que les scores de différence sont la variable 1 moins la variable 2 et non l’inverse, donc si nous voulons que l’amélioration corresponde à une différence de valeur positive, nous voulons en fait que « test 2 » soit notre « variable 1 ». De même, nous dirions que \(\mu_{D} = \mu_{1}-\mu_{2}\) est la moyenne de population pour cette variable de différence. Donc, pour convertir ceci en un test d’hypothèse, notre hypothèse nulle est que cette différence moyenne est nulle et l’hypothèse alternative est que ce n’est pas le cas.

\[\text{H}_{0} : \mu_{D}=0\\ \text{H}_{1} : \mu_{D}\neq 0\]

En supposant qu’il s’agit d’un test à deux volets. Ceci est plus ou moins identique à la façon dont nous avons décrit les hypothèses du test t pour un échantillon. La seule différence est que la valeur spécifique prédite par l’hypothèse nulle est 0, de sorte que notre statistique t est définie à peu près de la même manière. Si nous laissons \(\bar{D}\) indiquer la moyenne des scores de différence, alors :

\[ t = \frac{\bar{D}}{SE(\bar{D})} \]

Lequel correspond à

\[ t = \frac{\bar{D}}{\hat{\sigma}_{D}/\sqrt{N}} \]

Où \({\hat{\sigma}}_{D}\) est l’écart-type des scores de différence. Puisqu’il ne s’agit que d’un test t ordinaire, sur un échantillon, sans rien de particulier, les degrés de liberté sont toujours N - 1. Et c’est tout. Le test t pour échantillons appariés n’est vraiment pas un nouveau test du tout. Il s’agit d’un test t à un échantillon, mais appliqué à la différence entre deux variables. C’est en fait très simple. La seule raison pour laquelle il mérite une discussion aussi longue que celle que nous venons de traverser est que vous devez être capable de reconnaître quand un test d’échantillons pour échantillons appariés est approprié, et de comprendre pourquoi c’est mieux qu’un test t pour échantillons indépendants.

11.5.3 Faire le test avec Jamovi

Comment faire un t-test d’échantillons appariés avec Jamovi ? Une possibilité est de suivre le processus que j’ai décrit ci-dessus. C’est-à-dire, créer une variable de « différence » et ensuite exécuter un test t pour un échantillon sur cette variable. Puisque nous avons déjà créé une variable appelée amélioration, faisons cela et voyons ce que nous obtenons, Figure 11‑15.

Figure 11‑15 : Résultats d’un test t d’un échantillon sur des scores de différence appariés

Le résultat illustré à la Figure 11‑15 est (évidemment) formaté exactement de la même façon que la dernière fois que nous avons utilisé l’analyse « One Sample T-Test » (section 11.2), et cela confirme notre intuition. Il y a une amélioration moyenne de 1,4 % entre le test 1 et le test 2, ce qui est très différent de 0 (\(t(19) = 6,48, p< .001\)).

Cependant, supposons que vous soyez paresseux et que vous ne vouliez pas faire tout l’effort de créer une nouvelle variable. Ou peut-être voulez-vous simplement que la différence entre les tests à un échantillon et les tests à deux échantillons reste claire dans votre tête. Si c’est le cas, vous pouvez utiliser l’analyse de Jamovi « Paired Samples T-Test » pour obtenir les résultats présentés à la Figure 11‑16.

Figure 11‑16 : Résultats d’un test t d’échantillon apparié. Comparer avec la Figure 11‑15

Les chiffres sont identiques à ceux qui proviennent de l’analyse sur un seul échantillon, puisque, nous le soulignons une nouvelle fois, l’analyse t-test pour échantillons appariés n’est au fond qu’une analyse sur un seul échantillon.

11.6 Tests unilatéraux

Lorsque j’ai présenté la théorie des tests d’hypothèse nulle, j’ai mentionné qu’il y a certaines situations où il est approprié de spécifier un test unilatéral (voir la section 9.4.3). Jusqu’à présent, tous les tests ont été effectués de façon bliatérale. Par exemple, lorsque nous avons spécifié un test t sur un échantillon pour les notes de la classe de M. Zeppo, l’hypothèse nulle était que la vraie moyenne était de 67,5. L’autre hypothèse était que la moyenne réelle était supérieure ou inférieure à 67,5. Supposons que nous ne nous intéressions qu’à savoir si la vraie moyenne est supérieure à 67,5, et que nous n’ayons aucun intérêt à tester pour savoir si la vraie moyenne est inférieure à 67,5. Si tel est le cas, notre hypothèse nulle serait que la vraie moyenne est de 67,5 ou moins, et l’hypothèse alternative serait que la vraie moyenne est supérieure à 67,5. Dans Jamovi, pour l’analyse « One Sample T-Test », vous pouvez le spécifier en cliquant sur l’option « > Test Value », sous « Hypothesis ». Une fois que vous avez fait cela, vous obtiendrez les résultats comme indiqué en Figure 11‑17.

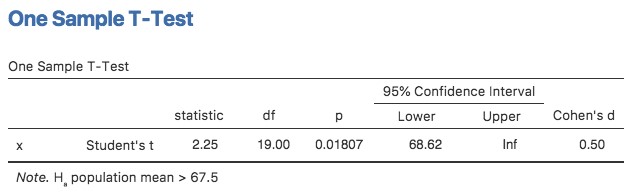
Figure 11‑17 : résultats de Jamovi montrant un « test t sur un échantillon »où l’hypothèse réelle est unilatérale, c’est-à-dire que la vraie moyenne est supérieure à 67,5.

Notez qu’il y a quelques changements par rapport au résultat que nous avons vu la dernière fois. Le plus important est le fait que l’hypothèse réelle a changé, pour refléter les différents tests. La deuxième chose à noter est que bien que la statistique t et les degrés de liberté n’aient pas changé, la valeur p a changé. Cela s’explique par le fait que le test unilatéral a une zone de rejet différente de celle du test bilatéral. Si vous avez oublié pourquoi et ce que cela signifie, vous pouvez relire le chapitre 9, et la section 9.4.3 en particulier. La troisième chose à noter est que l’intervalle de confiance est lui aussi différent : il fait désormais état d’un intervalle de confiance « unilatéral » plutôt que bilatéral. Dans un intervalle de confiance bilatéral, nous essayons de trouver les nombres a et b de telle sorte que nous sommes convaincus que, si nous devions répéter l’étude plusieurs fois, alors 95% du temps la moyenne se situerait entre a et b. Dans un intervalle de confiance unilatéral, nous essayons de trouver un seul nombre a tel que nous sommes convaincus que 95% du temps la vraie moyenne serait supérieure à a (ou inférieure à a si vous sélectionnez Measure 1 < Measure 2 dans la section « Hypothesis »).

C’est donc comme ça qu’on fait un t-test unilatéral d’un échantillon. Cependant, toutes les versions du test t peuvent être unilatérales. Pour un test t d’échantillons indépendants, vous pourriez avoir un test unilatéral si vous êtes seulement intéressé à vérifier si le groupe A a des scores plus élevés que le groupe B, mais n’avez aucun intérêt à savoir si le groupe B a des scores plus élevés que le groupe A. Supposons que, pour la classe du Dr Harpo, vous vouliez voir si les élèves d’Anastasia ont des notes supérieures à celle de Bernadette. Pour cette analyse, dans les options « Hypothèse », précisez que « Groupe 1 < Groupe2. Vous devriez obtenir les résultats illustrés à la Figure 11‑18.

Figure 11‑18 : résultats de Jamovi montrant un ’Test t d’échantillons indépendants » où l’hypothèse réelle est unilatérale, c’est-à-dire que les étudiants d’Anastasia avaient des notes supérieures à ceux de Bernadette.

Encore une fois, le résultat change de façon prévisible. La définition de l’hypothèse alternative a changé, la valeur p a changé, et elle fait maintenant état d’un intervalle de confiance unilatéral plutôt que bilatéral.

Qu’en est-il du test t des échantillons appariés ? Supposons que nous voulions tester l’hypothèse que les notes augmentent du test 1 au test 2 dans la classe de M. Zeppo, et que nous ne sommes pas prêts à considérer l’idée que les notes diminuent. Dans Jamovi vous le feriez en spécifiant, sous l’option « Hypothesis », que grade test2 (« Measure 1 » dans Jamovi, parce que nous l’avons d’abord copié dans la boîte des variables appariées) > grade test1 (« Measure 2 » dans Jamovi). Vous devriez obtenir les résultats illustrés à la Figure 11‑19.

Figure 11‑19 : résultats de Jamovi montrant un « Test t d’échantillons appariés » où l’hypothèse réelle est unilatérale, c’est-à-dire que le grade test2 (Mesure 1) > grade test1 (Measure 2)

Encore une fois, la production change de façon prévisible. L’hypothèse a changé, la valeur p a changé et l’intervalle de confiance est maintenant unilatéral.

11.7 Taille de l’effet

La mesure de l’ampleur de l’effet la plus couramment utilisée pour un test t est le *d de Cohen** (Cohen 1988). C’est une mesure très simple en principe, avec pas mal de rides quand on commence à creuser dans les détails. Cohen lui-même l’a défini principalement dans le contexte d’un test t d’échantillons indépendants, en particulier le test de Student. Dans ce contexte, une façon naturelle de définir la valeur de l’effet est de diviser la différence entre les moyennes par une estimation de l’écart-type. En d’autres termes, nous cherchons à calculer quelque chose dans ce sens :

\[ d = \frac{\left(\text{moyenne 1} \right) - (\text{moyenne 2})}{\text{std dev}} \]

et il a suggéré un guide approximatif pour l’interprétation d dans le Tableau 11‑1. On pourrait penser que ce serait assez clair, mais ce n’est pas le cas. C’est en grande partie parce que Cohen n’était pas assez précis sur ce qui, selon lui, devrait être utilisé comme mesure de l’écart-type (pour sa défense, il essayait d’adopter un point de vue plus large dans son livre, et non des détails mineurs). Comme l’ont mentionné McGrath et Meyer (2006), il existe plusieurs versions différentes d’usage courant, et chaque auteur a tendance à adopter une notation légèrement différente. Par souci de simplicité (par opposition à l’exactitude), j’utiliserai d pour faire référence à toute statistique calculée à partir de l’échantillon, et j’utiliserai \(\delta\) pour faire référence à un effet dans la population théorique. Évidemment, cela signifie qu’il y a plusieurs choses différentes, toutes appelées d.

Tableau 11‑1 : Un guide (très) grossier pour interpréter le d. de Cohen. Ma recommandation personnelle est de ne pas les utiliser à l’aveuglette. La statistique d a une interprétation naturelle en soi. Il décrit la différence entre les moyennes comme étant le nombre d’écarts-types qui sépare ces moyennes. C’est donc généralement une bonne idée de réfléchir à ce que cela signifie en termes pratiques. Dans certains contextes, un « petit » effet pourrait avoir une grande importance pratique. Dans d’autres situations, un effet « important » peut ne pas être très intéressant.

valeur d	interprétation approximative
environ 0,2	«Effet « petit
environ 0,5	«effet « modéré
environ 0,8	«effet « grand

Je pense que le seul cas où vous voudriez utiliser le d de Cohen, c’est lorsque vous exécutez un test t, et Jamovi a la possibilité de calculer la taille de l’effet pour toutes les variantes de test t qu’il propose.

11.7.1 d de Cohen sur un échantillon

La situation la plus simple à considérer est celle qui correspond à un test t sur un échantillon. Dans ce cas, il s’agit de la moyenne \(\bar{X}\) d’un échantillon et de la moyenne \(\mu_{0}\) d’une population (hypothétique) à laquelle la comparer. De plus, il n’y a qu’une seule façon raisonnable d’estimer l’écart-type de la population. Nous utilisons simplement notre estimateur habituel \(\hat{\sigma}\). Par conséquent, nous nous retrouvons avec ce qui suit comme seule façon de calculer d

\[ d = \frac{\bar{X} - \sigma_{0}}{\hat{\sigma}} \]

Lorsqu’on examine les résultats de la Figure 11‑6, la valeur de taille de l’effet est la valeur du d de Cohen = 0,50. Dans l’ensemble, les étudiants en psychologie de la classe du Dr Zeppo obtiennent donc des notes (moyenne = 72,3) qui sont d’environ 0,5 écarts-types plus élevés que le niveau auquel vous vous attendriez (67,5) s’ils se situaient au même niveau que les autres étudiants. Si l’on en juge par le guide approximatif de Cohen, il s’agit d’un effet de taille modérée.

11.7.2 d de Cohen à partir d’un test t de Student

La majorité des discussions sur le d de Cohen se concentrent sur une situation analogue au test t de Student des échantillons indépendants , et c’est dans ce contexte que l’histoire devient plus confuse, puisqu’il existe plusieurs versions différentes de d que vous pourriez utiliser dans cette situation. Pour comprendre pourquoi il existe plusieurs versions de d, il est utile de prendre le temps d’écrire une formule qui correspond à la taille réelle de l’effet de population \(\delta\). C’est assez simple,

\[ \delta = \frac{\mu_{1} - \mu_{2}}{\sigma} \]

où, comme d’habitude, \(\mu_{1}\) et \(\mu_{2}\) sont les moyennes de population correspondant respectivement au groupe 1 et au groupe 2, et \(\sigma\) est l’écart-type (identique pour les deux populations). La façon évidente d’estimer \(\delta\) est de faire exactement la même chose que dans le test t lui-même, c’est-à-dire d’utiliser les moyennes de l’échantillon dans numérateur et une estimation de l’écart type regroupé dénominateur.

\[ d = \frac{{\bar{X}}_{1} - {\bar{X}}_{2}}{{\hat{\sigma}}_{P}} \]

Où \({\hat{\sigma}}_{P}\) est exactement la même mesure de l’écart-type global qui apparaît dans le test t. C’est la version la plus couramment utilisée du d de Cohen lorsqu’il est appliquée aux résultats d’un test t de Student, et c’est celle fournie dans Jamovi. On l’appelle parfois la statistique g de Hedges (Hedges 1981).

Cependant, il y a d’autres possibilités que je vais décrire brièvement. Premièrement, vous pouvez avoir des raisons de ne vouloir utiliser qu’un seul des deux groupes comme base de calcul de l’écart-type. Cette approche (souvent appelée \(\Delta\) de Glass, prononcé delta) n’a de sens que lorsque l’on a de bonnes raisons de traiter l’un des deux groupes comme un reflet plus pur de « variation naturelle » que l’autre. Cela peut se produire si, par exemple, l’un des deux groupes est un groupe témoin. Deuxièmement, rappelons que dans le calcul habituel de l’écart-type global, nous divisons par N-2 pour corriger le biais dans la variance de l’échantillon. Dans une version du d de Cohen, cette correction est omise et nous la divisons par \(N\). Cette version a du sens surtout lorsqu’on essaie de calculer la taille de l’effet dans l’échantillon plutôt que d’estimer la taille de l’effet dans la population. Enfin, il existe une version basée sur Hedges et Olkin (2014), qui soulignent l’existence d’un léger biais dans l’estimation habituelle (globale) du d de Cohen. Ils introduisent donc une petite correction en multipliant la valeur habituelle de d par (N–3)/(N-2,25).

Laissons de côté toutes ces variations que vous pourriez utiliser si vous le vouliez et jetons un coup d’œil à la version par défaut dans Jamovi. Dans la Figure 11‑10 d de Cohen = 0,74, ce qui indique que les notes des élèves de la classe d’Anastasia sont, en moyenne, de 0,74 écart-type supérieurs aux notes des élèves de la classe de Bernadette. Pour un test de Welch, la taille de l’effet estimé est la même (Figure 11‑12).

11.7.3 d de Cohen pour un test t sur des échantillons appariés

Enfin, que devrions-nous faire pour un test t sur des échantillons appariés ? Dans ce cas, la réponse dépend de ce que vous essayez de faire. Jamovi suppose que vous voulez mesurer l’ampleur de votre effet par rapport à la distribution des scores de différence, et la mesure de d que vous calculez est :

\[ d = \frac{\bar{D}}{{\hat{\sigma}}_{D}} \]

Où \({\hat{\sigma}}_{D}\) est l’estimation de l’écart-type des différences. Dans la Figure 11‑16, d de Cohen = 1,45, ce qui indique que les notes au temps 2 sont, en moyenne, de 1,45 écart-type plus élevées que les notes au temps 1.

C’est la version du d de Cohen qui est utilisé par l’analyse Jamovi « Paired Samples T-Test ». Le seul problème, c’est de savoir si c’est la mesure que vous voulez ou non. Dans la mesure où vous vous souciez des conséquences pratiques de votre recherche, vous voulez souvent mesurer la taille de l’effet par rapport aux variables initiales, et non les scores de différence (par exemple, l’amélioration de 1% dans la classe du Dr Chico au fil du temps est assez faible par rapport à la variation des notes entre étudiants), auquel cas vous utiliserez les mêmes versions du d de Cohen’s que celles vous utiliseriez pour un test Student ou Welch. Ce n’est pas si simple de le faire en Jamovi ; il faut en fait modifier la structure des données dans la feuille de données alors je vais pas vous en parler ici.⁸⁸, mais le d de Cohen pour cette perspective est très différent : il est de 0,22 ce qui est assez petit quand on l’évalue sur l’échelle des variables originales.

11.8 Vérification de la normalité d’un échantillon

Tous les tests dont nous avons discuté jusqu’ici dans ce chapitre ont supposé que les données sont normalement distribuées. Cette hypothèse est souvent tout à fait raisonnable, car le théorème central limite (section 8.3.3) tend à garantir que de nombreuses quantités du monde réel sont normalement réparties. Chaque fois que vous soupçonnez que votre variable est en fait une moyenne de beaucoup de choses différentes, il y a de fortes chances qu’elle soit normalement distribuée, ou au moins assez proche de la normale pour que vous puissiez vous en tirer avec tests t. Cependant, la vie n’offre pas de garanties, et il y a d’ailleurs de nombreuses situations où on se retrouve avec des variables qui sont complètement anormales. Par exemple, chaque fois que vous pensez que votre variable est en fait le minimum de beaucoup de choses différentes, il y a de très bonnes chances qu’elle finisse de façon assez asymétrique. En psychologie, les données sur le temps de réponse (TR) en sont un bon exemple. Si vous supposez qu’il y a beaucoup de choses qui pourraient déclencher une réponse d’un sujet humain, alors la réponse réelle se produira la première fois qu’un de ces événements déclencheurs se produit.⁸⁹ Cela signifie que les données des TR sont systématiquement non normales. Bien, donc si la normalité est assumée par tous les tests, et qu’elle est satisfaite la plupart du temps mais pas toujours (au moins approximativement) par les données du monde réel, comment pouvons-nous vérifier la normalité d’un échantillon ? Dans cette section, j’aborde deux méthodes : les diagrammes QQ et le test Shapiro-Wilk.

11.8.1 Les diagrammes QQ

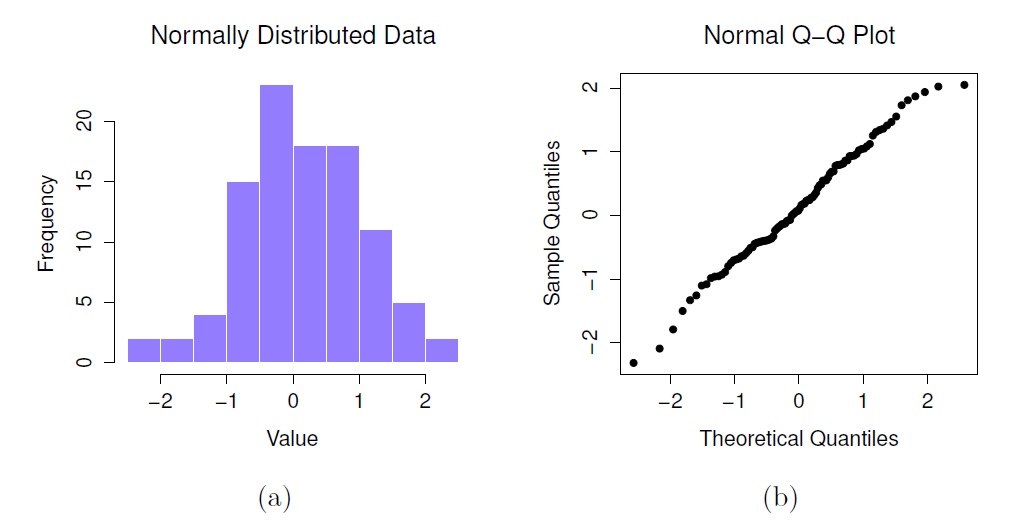
Figure 11‑20 : Histogramme (figure a) et graphique QQ normal (figure b) de données normales, un échantillon normalement distribué avec 100 observations. La statistique Shapiro-Wilk associée à ces données est W = .99, ce qui indique qu’aucun écart significatif par rapport à la normalité n’a été détecté (p = .73)

Une façon de vérifier si un échantillon viole l’hypothèse de normalité est de dessiner un « graphique QQ » (graphique Quantile-Quantile). Cela vous permet de vérifier visuellement si vous constatez des violations systématiques. Dans un graphique QQ, chaque observation est tracée comme un point unique. La coordonnée x est le quantile théorique dans lequel l’observation devrait se situer si les données étaient normalement distribuées (avec la moyenne et la variance estimées à partir de l’échantillon), et sur la coordonnée y est le quantile réel des données dans l’échantillon. Si les données sont normales, les points doivent former une ligne droite. Par exemple, voyons ce qui se passe si nous générons des données en échantillonnant à partir d’une distribution normale, puis en dessinant un graphique QQ. Les résultats sont présentés à la Figure 11‑20. Comme vous pouvez le constater, ces données forment une ligne assez droite ; ce qui n’est pas surprenant étant donné que nous les avons échantillonnées à partir d’une distribution normale ! Par contre, examinez les deux ensembles de données illustrés à la Figure 11‑21. Les panneaux supérieurs montrent l’histogramme et un graphique QQ pour un ensemble de données très asymétrique : le tracé QQ se courbe vers le haut. Les figures inférieures montrent les mêmes tracés pour un ensemble de données à forte kurtose : dans ce cas, le tracé QQ s’aplatit au milieu et s’incurve fortement à chaque extrémité.

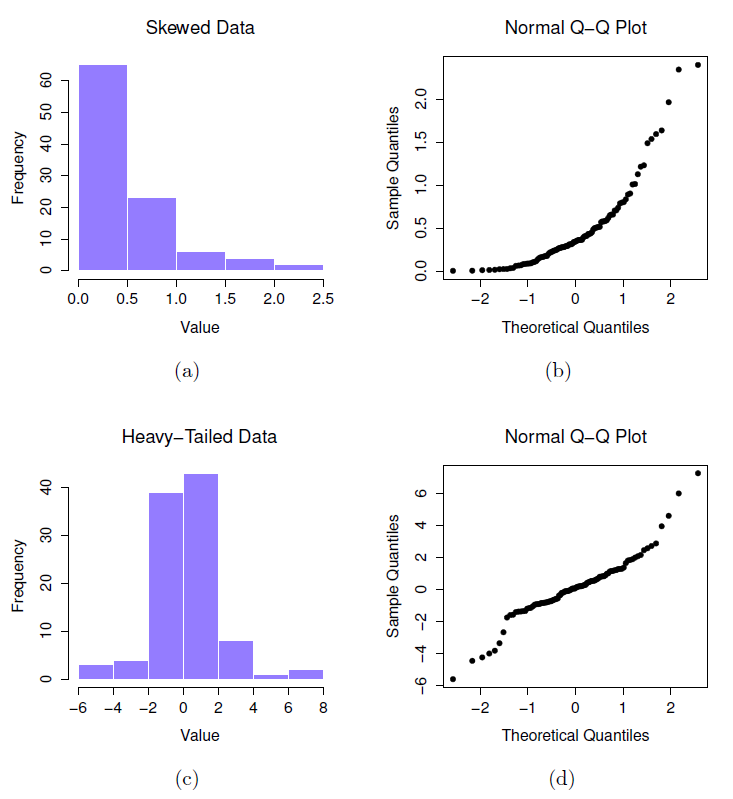
Figure 11‑21 : Dans la rangée du haut, un histogramme (figure a) et un graphique QQ normal (figure b) des 100 observations d’un ensemble de données skewed.data. L’asymétrie des données ici est de 1,94 et se reflète dans un graphique QQ qui s’incurve vers le haut. En conséquence, la statistique de Shapiro-Wilk est W = .80, ce qui reflète un écart important par rapport à la normalité (p < .001). La rangée du bas montre les mêmes graphiques pour un ensemble de données à queues pointues, qui se compose de 100 observations. Dans ce cas, les queues pointues dans les données produisent une kurtosis élevée (2,80), et provoquent l’aplatissement de la courbe QQ au milieu, et une forte courbe de chaque côté. La statistique Shapiro-Wilk résultante est W = .93, ce qui reflète une fois de plus une non-normalité importante (p < .001).

11.8.2 Tests Shapiro-Wilk

Les graphiques QQ fournissent un bon moyen de vérifier de façon informelle la normalité de vos données, mais parfois vous voudrez faire quelque chose d’un peu plus formel et le test Shapiro-Wilk (Shapiro and Wilk 1965) est probablement ce que vous recherchez.⁹⁰ Comme on peut s’y attendre, l’hypothèse nulle testée est qu’un ensemble de N observations est normalement distribué.

La statistique du test qu’il calcule est conventionnellement désignée par W, et elle est calculée comme suit. Tout d’abord, nous trions les observations par ordre croissant de taille, X₁ étant la plus petite valeur de l’échantillon, X₂ étant la deuxième plus petite et ainsi de suite. Ensuite, la valeur de W est donnée par :

\[ W = \frac{\left( \sum_{i = 1}^{N}{a_{i}X_{i}} \right)^{2}}{{\sum_{i = 1}^{N}\left( X_{i} - \bar{X} \right)}^{2}} \]

où \(\bar{X}\) est la moyenne des observations, et les valeurs de ai sont … heu … quelque chose de compliqué qui dépasse un peu la portée d’un texte d’introduction.

Comme il est un peu difficile d’expliquer les mathématiques qui se cachent derrière la statistique W, il est préférable de donner une description générale de la façon dont elle se comporte. Contrairement à la plupart des statistiques de test que nous rencontrerons dans ce livre, ce sont en fait de petites valeurs de W qui indiquent un écart par rapport à la normalité. La statistique W a une valeur maximale de 1, ce qui se produit lorsque les données semblent « parfaitement normales ». Plus la valeur de W est petite, moins les données sont normales. Cependant, la distribution d’échantillonnage pour \(W\), qui n’est pas l’une des distributions standard dont j’ai parlé au chapitre 7 et qui est en fait un casse-tête, dépend de la taille de l’échantillon N. Pour vous donner une idée de ce à quoi ressemblent ces distributions, j’en ai représenté trois à la Figure 11‑22. Notez que, à mesure que la taille de l’échantillon commence à augmenter, la distribution d’échantillonnage devient très serrée près de W=1, et par conséquent, pour les échantillons plus grands, W n’a pas besoin d’être beaucoup plus petit que 1 pour que le test soit significatif.

Pour obtenir la statistique Shapiro-Wilk dans les tests t avec Jamovi, cochez l’option « Normalité » sous « Hypothesis ». Dans les données échantillonnées au hasard (N = 100) que nous avons utilisées pour la courbe QQ, la valeur de la statistique du test de normalité de Shapiro-Wilk était W = 0,99 avec une valeur p de 0,69. Il n’est donc pas surprenant que nous n’ayons aucune preuve que ces données s’écartent de la normalité. Lorsque vous rapportez les résultats d’un test Shapiro-Wilk, vous devriez (comme d’habitude) vous assurer d’inclure la statistique du test W et la valeur p, mais la distribution d’échantillonnage dépend tellement de N qu’il serait probablement bienvenu d’inclure également N.

11.8.3 Exemple

En attendant, cela vaut probablement la peine de vous montrer un exemple de ce qui arrive au graphiques QQ et au test de Shapiro-Wilk quand les données ne sont pas normales.

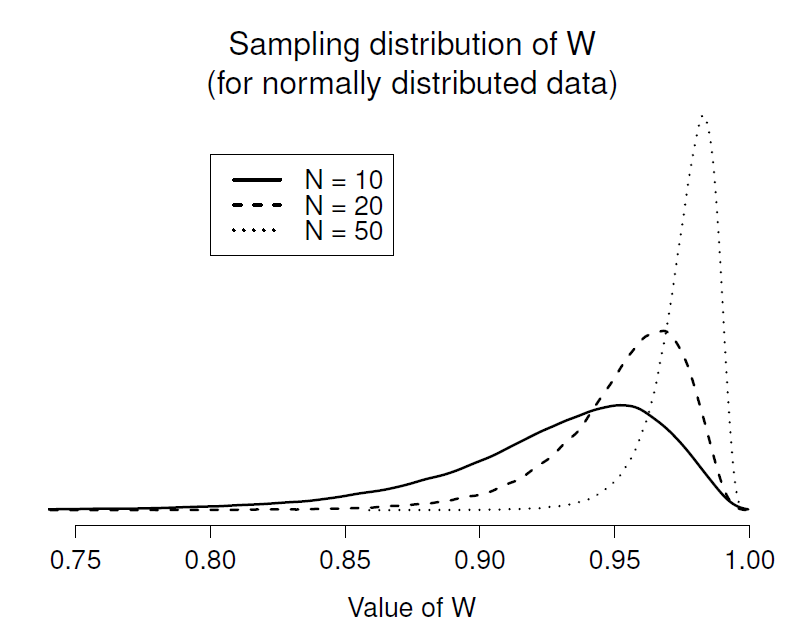
Figure 11‑22 : Distribution d’échantillonnage de la statistique Shapiro-Wilk W, sous l’hypothèse nulle que les données sont normalement distribuées, pour des échantillons de taille 10, 20 et 50. Notez que les petites valeurs de W indiquent un écart par rapport à la normalité.

Pour cela, regardons la distribution de nos données de AFL winning margins, qui, si vous vous souvenez bien, au chapitre 4, ne semblaient pas du tout provenir d’une distribution normale. Voici ce qui arrive au graphique QQ :

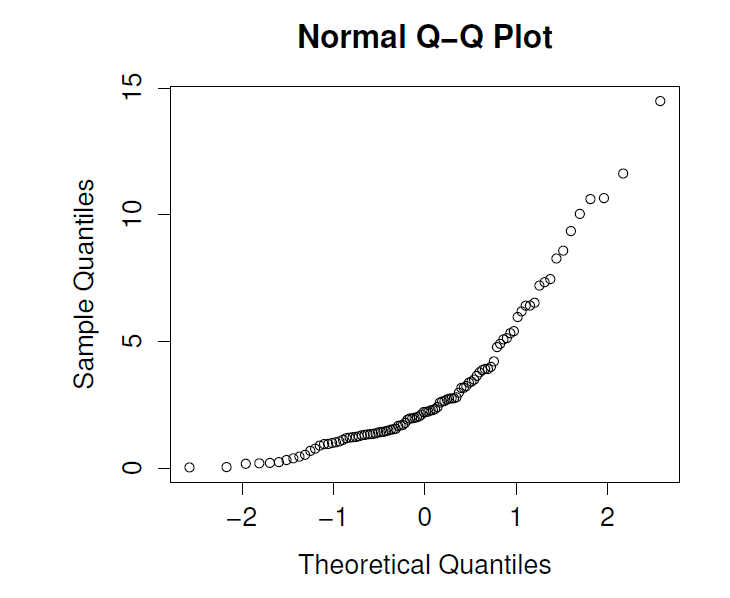
Et lorsque nous exécutons le test Shapiro-Wilk sur les données des AFL margins, nous obtenons une valeur pour la statistique du test de normalité Shapiro-Wilk de W = 0,94, et une valeur p = 9,481e-07. Un effet clairement significatif !

11.9 Tester des données non-normales avec des tests de Wilcoxon

Bien, supposons que vos données s’avèrent être substantiellement non-normales, mais que vous voulez quand même faire un test t? Cette situation se produit souvent dans la vie réelle. Pour les données AFL winning margins, par exemple, le test Shapiro-Wilk a montré très clairement que l’hypothèse de normalité est violée. C’est la situation dans laquelle vous voulez utiliser les tests Wilcoxon.

Comme le test t, le test de Wilcoxon se présente sous deux formes, pour un échantillon et pour deux échantillons, et ils sont utilisés dans plus ou moins les mêmes situations que les tests t correspondants. Contrairement au test t, le test de Wilcoxon ne suppose pas la normalité, ce qui est bien. En fait, ils ne font aucune supposition quant au type de distribution en cause. Dans le jargon statistique, ce sont en fait des tests non paramétriques. Bien qu’éviter l’hypothèse de normalité soit une bonne chose, il y a un inconvénient : le test de Wilcoxon est habituellement moins puissant que le test t (c.-à-d. un taux d’erreur de type II plus élevé). Je ne parlerai pas des tests de Wilcoxon aussi en détail que des tests t, mais je vais vous en donner un bref aperçu.

11.9.1 Test Mann-Whitney U à deux échantillons

Je commencerai par décrire le test Mann-Whitney U, puisqu’il est en fait plus simple que la version à échantillon unique. Supposons que nous ayons les résultats de 10 personnes à un test. Puisque mon esprit m’a complètement déçu, faisons comme s’il s’agissait d’un « test de génialité » et que nous ayons deux groupes de personnes, « A » et « B ». Je suis curieux de savoir quel groupe est le plus génial. Les données sont incluses dans le fichier awesome.csv, et il y a deux variables en dehors de la variable ID habituelle : scores et groupe.

Tant qu’il n’y a pas d’égalité (c.-à-d. des personnes ayant exactement le même score de génialité), le test que nous voulons faire est étonnamment simple. Tout ce que nous avons à faire est de construire un tableau qui compare chaque observation du groupe A à chaque observation du groupe B. Lorsque le point de référence du groupe A est plus grand, nous plaçons une coche dans le tableau :

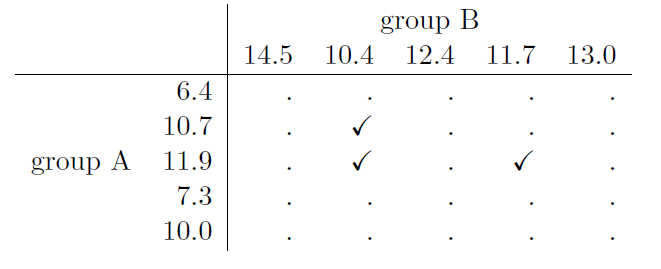
Nous comptons ensuite le nombre de cases à cocher. Voici notre statistique de test, W⁹¹. La distribution d’échantillonnage réelle pour W est quelque peu compliquée, et je vais sauter les détails. Pour nos besoins, il suffit de noter que l’interprétation de W est qualitativement la même que l’interprétation de t ou z. Autrement dit, si nous voulons un test bilatéral, nous rejetons l’hypothèse nulle lorsque W est très grand ou très petit, mais si nous avons une hypothèse orientée (c’est-à-dire unilatérale), nous utilisons seulement l’une ou l’autre.

Dans Jamovi, si nous exécutons un « T-Test d’échantillons indépendants » avec scores comme variable dépendante et un group comme variable de regroupement, et que nous cochons sous « tests » l’option « Mann-Whitney U », nous aurons des résultats montrant que U = 3 (c’est-à-dire le même nombre de marques de contrôle comme montré ci-dessus) et une valeur p=0,05556.

11.9.2 test de Wilcoxon pour un échantillon

Qu’en est-il du test de Wilcoxon sur un échantillon (ou de son équivalent, le test de Wilcoxon sur des échantillons appariés) ? Supposons que je sois intéressé à savoir si le fait de suivre un cours de statistique a un effet sur le bonheur des élèves. Mes données sont dans le fichier happiness.csv. Ce que j’ai mesuré ici, c’est le bonheur de chaque élève avant et après le cours, et le score de changement est la différence entre les deux. Tout comme nous l’avons vu avec le test t, il n’y a pas de différence fondamentale entre faire un test sur des échantillons appariés en utilisant les scores avant et après, et faire un test pour un échantillon unique en utilisant les scores de changement. Comme auparavant, la façon la plus simple de penser au test est de construire un tableau. La façon de procéder cette fois-ci consiste à prendre les scores de changement qui sont des différences positives et de les comparer à l’ensemble de l’échantillon. Ce que vous obtenez, c’est une table qui ressemble à ceci :

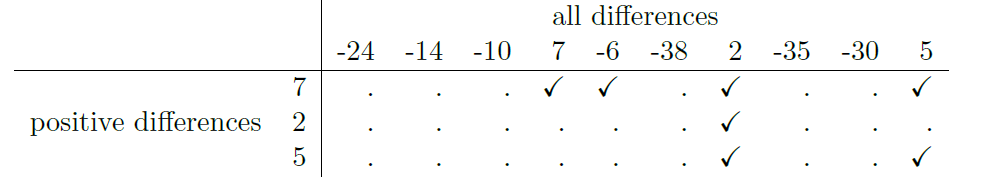
En comptant les marques cette fois-ci, nous obtenons une statistique de test de \(W=7\). Comme précédemment, si notre test est bilatéral, nous rejetons l’hypothèse nulle lorsque W est très grand ou très petit. Pour ce qui est de le calculer avec Jamovi, il est facile de savoir à quoi on peut s’attendre. Pour la version à un échantillon, vous spécifiez l’option « Wilcoxon rank » sous « Tests » dans la fenêtre d’analyse « One Sample T-Test ». Cela donne Wilcoxon \(W=7, p=0,03711\). Comme on peut le constater, nous avons un effet significatif. Évidemment, suivre un cours de statistique a un effet sur votre bonheur. Bien sûr, utiliser une version pour échantillons appariés du test ne nous donnera pas une réponse différente; voir Figure 11‑23.

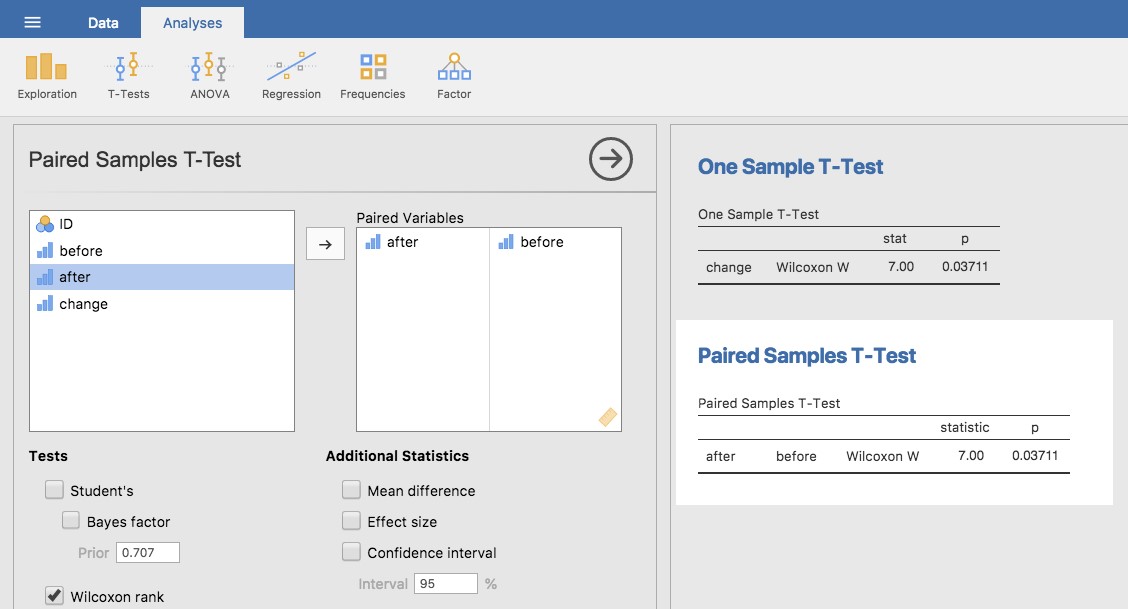
Figure 11‑23 : Copie d’écran Jamovi montrant les résultats pour le test non paramétrique W de Wilcoxon sur un échantillon et des échantillons appariés

11.10 Résumé

• Un test t sur un échantillon permet de comparer la moyenne d’un seul échantillon à une valeur hypothétique de la moyenne de la population. (Section 11.2)

• Un test t d’échantillons indépendants est utilisé pour comparer les moyennes de deux groupes et tester l’hypothèse nulle qu’ils ont la même moyenne. Il se présente sous deux formes : le test de Student (section 11.3) suppose que les groupes ont le même écart-type, mais pas le test de Welch (section 11.4).

• Un test t par paires d’échantillons est utilisé lorsque vous avez deux scores de chaque personne, et que vous voulez tester l’hypothèse nulle que les deux scores ont la même moyenne. Cela équivaut à prendre la différence entre les deux scores pour chaque personne, puis à effectuer test t sur un échantillon sur les scores de différence. (Section 11.5)

• Les tests unilatéraux sont parfaitement légitimes à condition qu’ils soient planifiés à l’avance. (Section 11.6)

• La taille de l’effet pour la différence entre les moyennes peut être calculée à l’aide de la statistique d de Cohen. (Section 11.7).

• Vous pouvez vérifier la normalité d’un échantillon à l’aide des graphiques QQ (non disponibles actuellement dans Jamovi) et du test Shapiro-Wilk. (Section 11.8)

• Si vos données sont anormales, vous pouvez utiliser les tests de Mann-Whitney ou de Wilcoxon au lieu des tests t. (Section 11.9)

References

Box, Joan Fisher. 1987. “Guinness, Gosset, Fisher, and Small Samples.” Statistical Science 2 (1): 45–52. https://doi.org/10.1214/ss/1177013437.

Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Hillsdale, N.J: L. Erlbaum Associates.

Hedges, Larry V. 1981. “Distribution Theory for Glass’s Estimator of Effect Size and Related Estimators.” Journal of Educational Statistics 6 (2): 107–28. https://doi.org/10.3102/10769986006002107.

Hedges, Larry V., and Ingram Olkin. 2014. Statistical Methods for Meta-Analysis. Academic Press.

McGrath, Robert E., and Gregory J. Meyer. 2006. “When Effect Sizes Disagree: The Case of R and d.” Psychological Methods 11 (4): 386–401. https://doi.org/10.1037/1082-989X.11.4.386.

Shapiro, S. S., and M. B. Wilk. 1965. “An Analysis of Variance Test for Normality (Complete Samples).” Biometrika 52 (3/4): 591–611. https://doi.org/10.2307/2333709.

Student, A. 1908. “The Probable Error of a Mean.” Biometrika 6 (1): 1–25. https://doi.org/10.1093/biomet/6.1.1.

Welch, B. L. 1947. “The Generalisation of Student’s Problems When Several Different Population Variances Are Involved.” Biometrika 34 (1-2): 28–35. https://doi.org/10.1093/biomet/34.1-2.28.

---

79. Des expériences informelles dans mon jardin suggèrent que oui, c’est vrai. Les plantes indigènes australiennes sont adaptées à de faibles niveaux de phosphore par rapport à n’importe où ailleurs sur terre, donc si vous avez acheté une maison avec un tas de plantes exotiques et que vous voulez planter des plantes indigènes, gardez-les séparés ; les nutriments des plantes européennes sont un poison pour les Australiennes.↩︎

80. En fait, c’est trop fort. Strictement parlant, le test z exige seulement que la distribution d’échantillonnage de la moyenne soit normalement distribuée. Si la population est normale, il s’ensuit nécessairement que la distribution d’échantillonnage de la moyenne est également normale. Cependant, comme nous l’avons vu en parlant du théorème de la limite centrale, il est tout à fait possible (voire banal) que la distribution d’échantillonnage soit normale même si la distribution de la population elle-même n’est pas normale. Cependant, à la lumière du ridicule de l’hypothèse selon laquelle l’écart-type véritable est connu, il n’y a vraiment pas beaucoup de raison d’entrer dans les détails à ce sujet !↩︎

81. Si j’ai bien compris l’histoire, Gosset n’a fourni qu’une solution partielle ; la solution générale au problème a été fournie par Sir Ronald Fisher.↩︎

82. Plus sérieusement, j’ai tendance à penser que l’inverse est vrai. Je me méfie beaucoup des rapports techniques qui remplissent leurs sections de résultats avec rien d’autre que des chiffres. C’est peut-être juste que je suis un crétin arrogant, mais j’ai souvent l’impression d’être un auteur qui ne fait aucun effort pour expliquer et interpréter son analyse au lecteur, ou qui ne la comprend pas lui-même, ou qui est un peu paresseux. Vos lecteurs sont intelligents, mais pas infiniment patients. Ne les ennuyez pas si vous pouvez l’éviter.↩︎

83. Un commentaire technique. De la même façon que nous pouvons affaiblir les hypothèses du test z pour ne parler que de la distribution d’échantillonnage, nous pouvons affaiblir les hypothèses du test t pour ne pas avoir à supposer la normalité de la population. Cependant, pour le t-test, c’est plus difficile à faire. Comme précédemment, nous pouvons remplacer l’hypothèse de normalité de la population par une hypothèse selon laquelle la distribution d’échantillonnage de \(\bar{X}\) est normale. Cependant, n’oubliez pas que nous nous basons également sur une estimation d’échantillon de l’écart-type, et nous exigeons donc aussi que la distribution d’échantillonnage de \(\hat{\sigma}\) soit le chi carré. Cela rend les choses plus désagréables, et cette version est rarement utilisée dans la pratique. Heureusement, si la répartition de la population est normale, ces deux hypothèses sont satisfaites.↩︎

84. Bien que ce soit le plus simple, c’est pourquoi j’ai commencé par lui.↩︎

85. Une drôle de question surgit presque toujours à ce moment-là : à quoi diable se réfère-t-on dans ce cas-ci ? Est-ce l’ensemble des étudiants qui suivent les cours du Dr Harpo (tous les 33) ? L’ensemble des personnes qui pourraient suivre le cours (un nombre inconnu d’entre elles) ? Ou autre chose ? Est-ce que ça a de l’importance de savoir ce que nous choisissons ? C’est la tradition dans un cours d’introduction aux statistiques comportementales de marmonner beaucoup à ce stade, mais comme mes élèves me posent cette question chaque année, je vais donner une brève réponse. Techniquement oui, c’est important. Si vous changez votre définition de ce qu’est réellement la population dans le “monde réel”, alors la distribution d’échantillonnage de votre moyenne observée change aussi. Le test t repose sur l’hypothèse que les observations sont échantillonnées au hasard dans une population infiniment grande et, dans la mesure où la vie réelle n’est pas comme ça, le test t peut être erroné. Dans la pratique, cependant, ce n’est généralement pas grand-chose. Même si l’hypothèse est presque toujours fausse, elle ne provoque pas beaucoup de biais du test, alors nous avons tendance à l’ignorer.↩︎

86. Une notation plus correcte sera introduite au chapitre 13.↩︎

87. Nous accueillons maintenant les Drs Harpo, Chico et Zeppo. Pas de récompense pour qui devine qui est le Dr Groucho.↩︎

88. Si vous êtes intéressé, vous pouvez voir comment cela a été fait dans le fichier chico2.omv↩︎

89. Il s’agit d’une sursimplification massive.↩︎

90. Vous pouvez aussi utiliser le test de Kolmogorov-Smirnov, qui est probablement plus traditionnel que le Shapiro-Wilk. Bien que la plupart de ce que j’ai pu lire semblent suggérer que Shapiro-Wilk est le meilleur test de normalité, le Kolomogorov-Smirnov est un test général d’équivalence distributive qui peut être adapté pour traiter d’autres types de tests de distribution. Dans Jamovi, le test Shapiro-Wilk est préférable.↩︎

91. En fait, il existe deux versions différentes de la statistique de test qui diffèrent l’une de l’autre par une valeur constante. La version que j’ai décrite est celle que Jamovi calcule↩︎