Chapitre 13 Comparaison de plusieurs moyennes (ANOVA à un facteur)

Ce chapitre présente l’un des outils statistiques les plus utilisés en psychologique, connu sous le nom « d’analyse de variance », mais généralement appelé ANOVA. La technique de base a été développée par Sir Ronald Fisher au début du XXe siècle et c’est à lui que nous devons cette terminologie plutôt malheureuse. Le terme ANOVA est un peu trompeur, à deux égards. Premièrement, bien que le nom de la technique fasse référence aux variances, ANOVA s’intéresse à l’étude des différences de moyennes. Deuxièmement, il y a plusieurs choses différentes que l’on appelle toutes des analyses de variance, dont certaines n’ont qu’un lien très ténu les unes avec les autres. Plus loin dans le livre, nous rencontrerons une gamme de différentes méthodes ANOVA qui s’appliquent dans des situations très différentes, mais pour les besoins de ce chapitre, nous ne considérerons que la forme la plus simple d’ANOVA, dans laquelle nous avons plusieurs groupes différents d’observations, et nous nous intéressons à à la différence entre ces groupes pour des variables résultats (variable dépendante) qui nous intéressent. C’est la question à laquelle répond une ANOVA à un facteur.

La structure de ce chapitre est la suivante : dans la Section 13.1, je vais introduire un ensemble de données fictives que nous utiliserons comme exemple courant dans tout le chapitre. Après avoir présenté les données, je décrirai la mécanique du fonctionnement réel d’une ANOVA à un facteur (Section 13.2), puis je me concentrerai sur la façon dont vous pouvez en exécuter une avec Jamovi (Section 13.3). Ces deux sections constituent le cœur du chapitre. Le reste du chapitre traite d’une série de sujets importants qui surviennent inévitablement lors de l’exécution d’une analyse de variance, à savoir comment calculer les valeurs de l’effet (section 13.4), les tests et corrections post hoc pour les comparaisons multiples (section 13.5) et les hypothèses sur lesquelles repose l’analyse de variance (section 13.6). Nous parlerons également de la façon de vérifier ces hypothèses et de ce que vous pouvez faire en cas de non-respect de ces hypothèses (sections 13.6.1 à 13.7). Ensuite, nous traiterons de l’ANOVA pour mesures répétées dans les sections 13.8 et 13.9. A la fin du chapitre, nous parlerons un peu de la relation entre l’analyse de variance et les autres outils statistiques (section 13.10).

13.1 Un ensemble de données illustratif

Supposons que vous avez participé à un essai clinique dans lequel vous testez un nouvel antidépresseur appelé Joyzepam. Afin d’établir un test équitable de l’efficacité du médicament, l’étude comprend trois médicaments distincts à administrer. L’un est un placebo et l’autre est un antidépresseur / médicament anti-anxiété appelé Anxifree. Un groupe de 18 participants souffrant de dépression modérée à sévère est recruté pour votre test initial. Comme les médicaments sont parfois administrés conjointement avec une thérapie psychologique, votre étude comprend 9 personnes qui suivent une thérapie cognitivo-comportementale (TCC) et 9 dont ce n’est pas le cas. Les participants sont assignés au hasard (selon la procédure du double aveugle, bien sûr) à un traitement, de sorte qu’il y a 3 personnes en TCC et 3 personnes sans traitement pour chacun des 3 médicaments. Un psychologue évalue l’humeur de chaque personne après trois mois de traitement avec chaque drogue, et l’amélioration globale de l’humeur de chaque personne est évaluée sur une échelle allant de -5 à +5. Avec ce plan d’étude, chargeons maintenant le fichier de données dans clinicaltrial.csv. Nous pouvons voir que cet ensemble de données contient les trois variables drug (médicament), therapy (thérapie) and mood.gain (amélioration de l’humeur).

Dans le cadre du présent chapitre, ce qui nous intéresse vraiment, c’est l’effet des médicaments sur l’amélioration de l’humeur. La première chose à faire est de calculer des statistiques descriptives et de faire des graphiques. Au chapitre 4, nous vous avons montré comment faire, et certaines des statistiques descriptives que nous pouvons calculer dans Jamovi sont présentées à la Figure 13‑1.

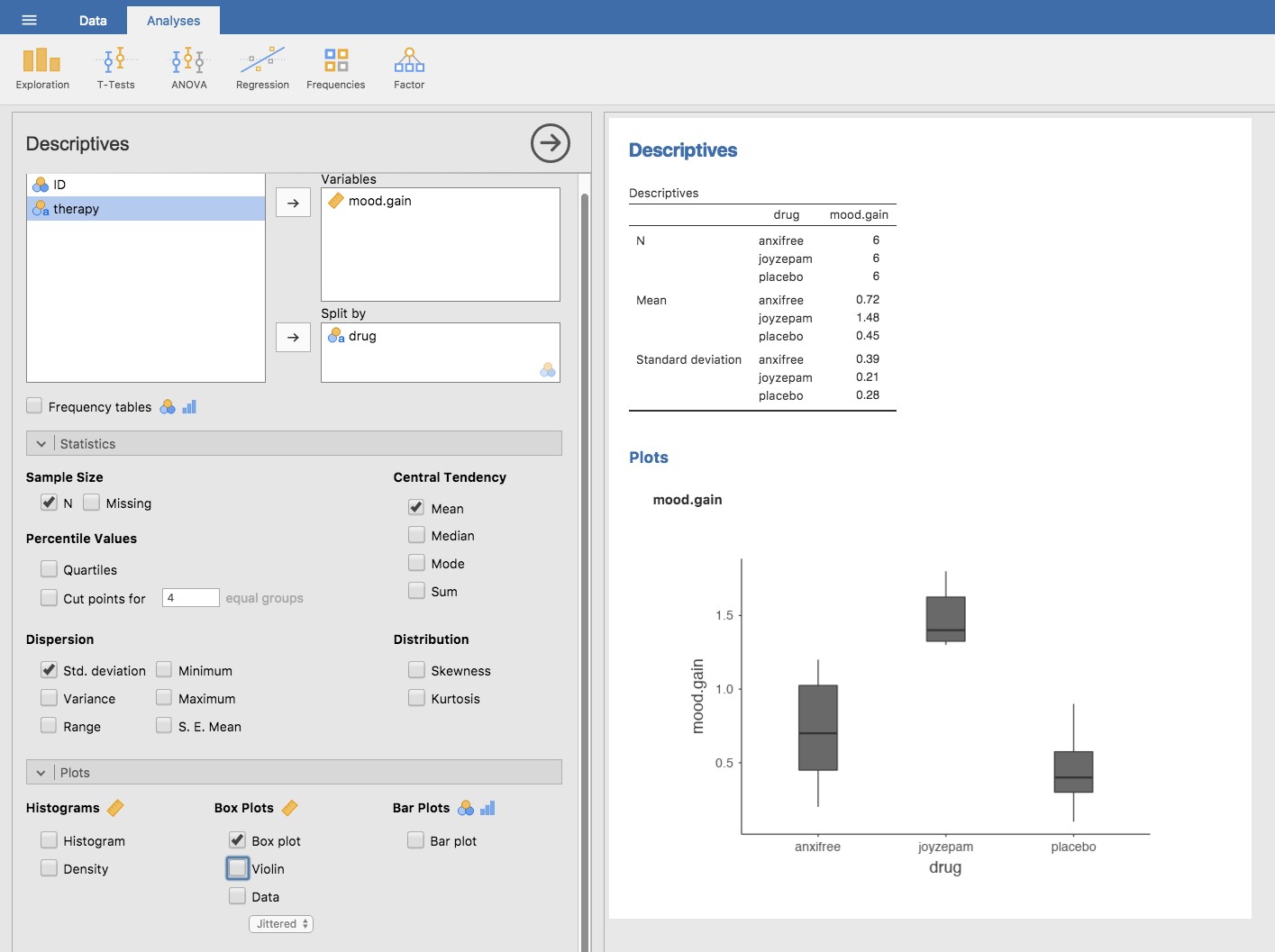
Figure 13‑1 : Statistiques descriptive sur l’amélioration de l’humeur et diagrammes en boîtes par médicament administré

Comme le montre clairement la figure, l’humeur des participants du groupe Joyzepam s’est améliorée davantage que celle des participants du groupe Anxifree ou du groupe placebo (témoin). Le groupe Anxifree présente une amélioration de l’humeur plus importante que le groupe témoin, mais la différence n’est pas aussi grande. La question à laquelle nous voulons répondre est la suivante : ces différences sont-elles « réelles » ou sont-elles dues au hasard ?

13.2 Comment fonctionne ANOVA

Afin de répondre à la question posée par les données de nos essais cliniques, nous allons procéder à une analyse de variance à un facteur. Je vais commencer par vous montrer comment le faire à la main, en construisant l’outil statistique à partir de zéro et en vous montrant comment vous pourriez le faire si vous n’aviez accès à aucune des fonctions ANOVA intégrées dans Jamovi. Et j’espère que vous le lirez attentivement, que vous essaierez de le faire une ou deux fois pour vous assurer de bien comprendre le fonctionnement d’ANOVA, et qu’une fois que vous aurez compris le concept, ne le referez plus jamais de cette façon.

Le plan expérimental que j’ai décrit dans la section précédente suggère fortement de nous intéresser à la comparaison du changement d’humeur moyen pour les trois différents médicaments. En ce sens, il s’agit d’une analyse similaire au test t (chapitre 11) mais impliquant plus de deux groupes. Si nous posons \(\mu_{P}\) pour la moyenne de la population pour le changement d’humeur induit par le placebo, et que \(\mu_{A}\) et \(\mu_{J}\) représentent les moyennes correspondantes à nos deux médicaments, Anxifree et Joyzepam, alors l’hypothèse nulle (quelque peu pessimiste) que nous voulons tester est que les trois moyennes de populations sont identiques. Autrement dit, aucun des deux médicaments n’est plus efficace qu’un placebo. Nous pouvons écrire cette hypothèse nulle comme :

H₀ : il est vrai que \(\mu_{P}=\mu_{A}=\mu_{J}\)

Par conséquent, notre hypothèse alternative est qu’au moins un des trois traitements différents est différent des autres. C’est un peu délicat d’écrire cela mathématiquement, parce que (comme nous le verrons plus loin) il y a plusieurs façons différentes dont l’hypothèse nulle peut être fausse. Donc pour l’instant, nous allons juste écrire l’hypothèse alternative comme ceci :

H₁ : il n’est pas vrai que \(\mu_{P}=\mu_{A}=\mu_{J}\)

Cette hypothèse nulle est beaucoup plus difficile à vérifier que toutes celles que nous avons vues auparavant. Comment allons-nous faire ? Une supposition raisonnable serait de « faire une analyse de variance », puisque c’est le titre du chapitre, mais il n’est pas particulièrement clair pourquoi une « analyse des variances » nous aidera à apprendre quoi que ce soit d’utile sur les moyennes. En fait, c’est l’une des plus grandes difficultés conceptuelles que les gens éprouvent lorsqu’ils rencontrent ANOVA pour la première fois. Pour voir comment cela fonctionne, je trouve très utile de commencer par parler des variances. En fait, je vais commencer par jouer à des jeux mathématiques avec la formule qui décrit la variance. C’est-à-dire, nous allons commencer par jouer avec les variances et il s’avérera que cela nous donne un outil utile pour étudier les moyennes.

13.2.1 Deux formules pour la variance de Y

Tout d’abord, commençons par introduire quelques notations. Nous utiliserons G pour faire référence au nombre total de groupes. Pour notre ensemble de données, il y a trois médicaments, il y a donc trois groupes G=3. Ensuite, nous utiliserons N pour faire référence à la taille totale de l’échantillon ; il y a un total de N = 18 personnes dans notre ensemble de données. De même, utilisons N_k pour indiquer le nombre de personnes dans le k-ème groupe. Dans notre essai clinique fictif, la taille de l’échantillon est de N_k=6 pour chacun des trois groupes.¹⁰⁹ Enfin, nous utiliserons Y pour désigner la variable de résultat. Dans notre cas, Y fait référence aux changements d’humeur. Plus précisément, nous utiliserons Y_ik pour faire référence au changement d’humeur vécu par le i-ème membre du k-ème groupe. De même, nous utiliserons \(\bar{Y}\) comme changement d’humeur moyen, pour l’ensemble des 18 personnes de l’expérience, et \({\bar{Y}}_{k}\) comme référence au changement d’humeur moyen vécu par les 6 personnes du groupe k.

Maintenant que nous avons réglé notre notation, nous pouvons commencer à écrire des formules. Pour commencer, rappelons la formule de variance que nous avons utilisée à la section 4.2, à l’époque où nous ne faisions que des statistiques descriptives. La variance d’échantillon de Y est définie comme suit

\[ \text{Var}\left( Y \right) = \frac{1}{N}\sum_{k = 1}^{G}{\sum_{i = 1}^{N_{k}}\left( Y_{\text{ik}} - \bar{Y} \right)^{2}} \]

Cette formule semble à peu près identique à celle de la variance de la section 4.2. La seule différence, c’est que cette fois-ci, j’ai deux résumés : Je fais la somme des groupes (c.-à-d. les valeurs pour k) et des personnes au sein des groupes (c.-à-d. les valeurs pour i). C’est un détail purement esthétique. Si j’avais plutôt utilisé la notation Y_p pour faire référence à la valeur de la variable de résultat pour la personne p dans l’échantillon, alors je n’aurais qu’une seule somme. La seule raison pour laquelle nous avons une double sommation ici est que j’ai classé les gens dans les groupes, puis attribué des numéros à des personnes au sein de groupes.

Un exemple concret pourrait être utile ici. Considérons ce tableau, dans lequel nous avons un total de N=5 personnes triées en groupes G=2. Arbitrairement, disons que les gens « cool » sont le groupe 1 et les gens « pas cool » sont le groupe 2, il s’avère que nous avons trois personnes cool (N₁=3) et deux personnes pas cool (N₂=2).

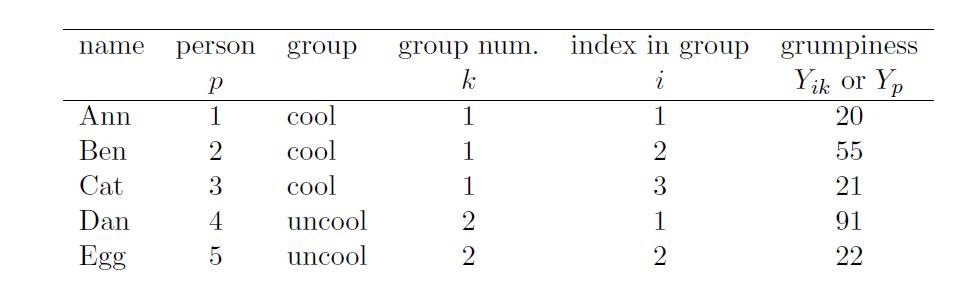
Notez que j’ai construit deux systèmes d’étiquetage différents ici. Nous avons une variable « personne » p, il serait donc tout à fait sensé de parler de Y_p comme de la grinchiosité de la p-ième personne de l’échantillon. Par exemple, le tableau montre que Dan est le quatrième, donc nous dirions p=4. Donc, quand on parle du caractère grincheux Y de « Dan », qui qu’il soit, on pourrait parler de sa grinchiosité en disant que Y_p=91, pour personne p=4, bien sûr. Cependant, ce n’est pas la seule façon de parler de Dan. Comme alternative, nous pourrions noter que Dan appartient au groupe « pas cool » (k=2), et est en fait la première personne listée dans le groupe pas cool (i=1). Il est donc tout aussi valable de faire référence à la mauvaise humeur de Dan en disant que Y_ik=91, où k=2 et i=1.

En d’autres termes, chaque personne p correspond à une combinaison ik unique, et donc la formule que j’ai donnée ci-dessus est en fait identique à notre formule originale pour la variance, qui serait

\[ \text{var}\left( Y \right) = \frac{1}{N}\sum_{p = 1}^{N}\left( Y_{p} - \bar{Y} \right)^{2} \]

Dans les deux formules, tout ce que nous faisons est de faire la somme de toutes les observations de l’échantillon. La plupart du temps, nous utiliserions simplement la notation Y_p la plus simple ; l’équation utilisant Y_p est clairement la plus simple des deux. Cependant, lorsque vous faites une analyse de variance, il est important de savoir quels participants appartiennent à quels groupes, et nous devons utiliser la notation avec Y_ik pour ce faire.

13.2.2 Des variances aux sommes de carrés

Bien, maintenant que nous avons une bonne idée de la façon dont la variance est calculée, définissons ce qu’on appelle la somme totale des carrés, qui est appelée SStot. C’est très simple. Au lieu de faire la moyenne quadratique des écarts , ce que nous faisons lorsque nous calculons la variance, nous nous contentons de les additionner.

La formule de la somme totale des carrés est donc presque identique à la formule de la variance

\[ \text{SS}_{\text{tot}} = \sum_{k = 1}^{G}{\sum_{i = 1}^{N_{k}}\left( Y_{\text{ik}} - \bar{Y} \right)^{2}} \]

Lorsque nous parlons d’analyser les variances dans le contexte d’ANOVA, ce que nous faisons en réalité, c’est de travailler avec les sommes totales des carrés plutôt que la variance en tant que telle. La propriété remarquable de la somme totale des carrés, c’est que nous pouvons la diviser en deux types différents de variation.

Tout d’abord, nous pouvons parler de la somme des carrés intra groupe, dans laquelle nous regardons à quel point chaque personne est différente de la moyenne de son propre groupe.

\[ \text{SS}_{w} = \sum_{k = 1}^{G}{\sum_{i = 1}^{N_{k}}\left( Y_{\text{ik}} - {\bar{Y}}_{k} \right)^{2}} \]

où \({\bar{Y}}_{k}\) est un groupe moyen. Dans notre exemple, \({\bar{Y}}_{k}\) serait le changement d’humeur moyen subi par les personnes qui reçoivent le k-ème médicament. Ainsi, au lieu de comparer les individus à la moyenne de toutes les personnes participant à l’expérience, nous les comparons seulement à ceux qui font partie du même groupe. Par conséquent, on s’attendrait à ce que la valeur de la SSw soit inférieure à la somme totale des carrés, parce qu’elle ne tient aucunement compte des différences entre les groupes, c.-à-d., si les médicaments ont des effets différents sur l’humeur des gens.

Ensuite, nous pouvons définir une troisième notion de variation qui saisit seulement les différences entre les groupes. Pour ce faire, nous examinons les différences entre la moyenne du groupe \({\bar{Y}}_{k}\) et la moyenne générale.

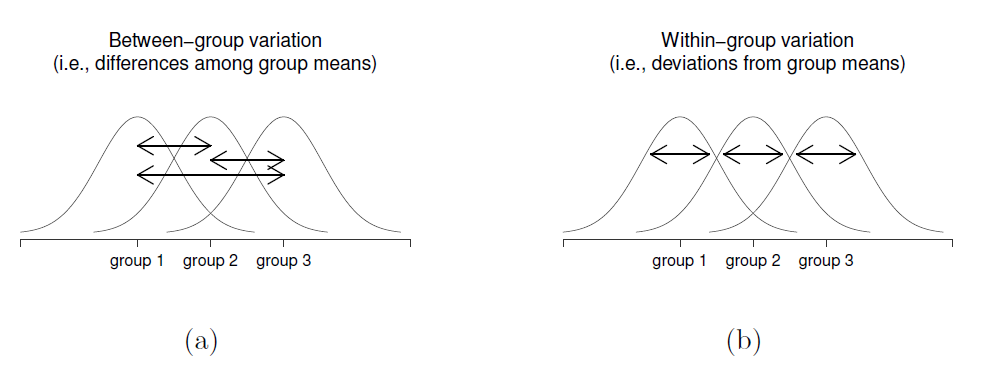
Figure 13‑2 : Illustration graphique de la variation « inter groupes » (figure a) et de la variation « intra groupes » (figure b). Sur la gauche, les flèches indiquent les différences entre les moyennes des groupes. Sur la droite, les flèches mettent en évidence la variabilité au sein de chaque groupe.

Afin de quantifier l’ampleur de cette variation, nous calculons la somme des carrés inter groupes.

\[\begin{aligned} \text{SS}_{b} & = \sum_{k = 1}^{G}{\sum_{i = 1}^{N_{k}}\left( {\bar{Y}}_{k} - \bar{Y} \right)^{2}}\\ & = \sum_{k = 1}^{G}{N_{k}\left( {\bar{Y}}_{k} - \bar{Y} \right)^{2}} \end{aligned} \]

Il n’est pas trop difficile de montrer que la variation totale entre les personnes dans l’expérience SStot est en fait la somme des différences inter groupes SSb et la variation intra groupes SSw. Nous avons donc,

\[ \text{SS}_{w}=\text{SS}_{b} + \text{SS}_{tot} \]

Bien, alors qu’est-ce qu’on a trouvé ? Nous avons découvert que la variabilité totale associée à la variable de résultat (SS_tot) peut être mathématiquement découpée en la somme de « la variation due aux différences dans les moyennes de l’échantillon pour les différents groupes » (SS_b) plus « le reste de la variation » (SS_w)¹¹⁰. En quoi cela m’aide-t-il à savoir que les groupes ont des moyennes de population différentes ? Mais attendez une seconde ! Maintenant que j’y pense, c’est exactement ce qu’on cherchait. Si l’hypothèse nulle est vraie, on s’attendrait à ce que tous les moyennes de l’échantillon soient assez semblables les uns des autres, non ? Et cela impliquerait qu’on s’attendrait à ce que SS_b soit vraiment petit, ou du moins à ce qu’il soit beaucoup plus petit que « la variation associée à tout le reste », SS_w. Je détecte un test d’hypothèse en cours de construction.

13.2.3 De la somme des carrés au test F

Comme nous l’avons vu dans la dernière section, l’idée qualitative derrière ANOVA est de comparer les deux sommes des carrés SS_b et SS_w entre elles. Si la variation inter groupes SSb est importante par rapport à la variation intra groupe SSw, nous avons des raisons de penser que les moyennes de population pour les différents groupes ne sont pas identiques entre elles. Pour convertir cela en un test d’hypothèse réalisable, il faut un peu de « bricoler ». Je vais d’abord vous montrer ce que nous faisons pour calculer notre statistique de test, le rapport F, puis vous donner une idée de la raison pour laquelle nous procédons de cette façon.

Afin de convertir nos valeurs SS en un rapport F, la première chose que nous devons calculer est le degré de liberté associé aux valeurs SS_b et SS_w. Comme d’habitude, les degrés de liberté correspondent au nombre de « données uniques » qui contribuent à un calcul particulier, moins le nombre de « contraintes » qu’ils doivent satisfaire. Pour la variabilité intra-groupe, nous calculons la variation des observations individuelles (N éléments de données) autour de la moyenne du groupe (contraintes G). En revanche, pour la variabilité inter groupes, nous nous intéressons à la variation de la moyenne du groupe (élements de données G) autour de la moyenne générale (1 contrainte). Par conséquent, les degrés de liberté sont ici :

\[ \text{df}_{b}= G-1\\ \text{df}_{w}= N-G \]

Bien, ça semble assez simple. Ensuite, nous convertissons nos sommes des carrés en une valeur les « carrés moyens », en divisant par les degrés de liberté :

\[ \text{MS}_{b} = \frac{\text{SS}_{b}}{\text{ddl}_{b}}\\ \text{MS}_{w} = \frac{\text{SS}_{w}}{\text{ddl}_{w}}\\ \]

Enfin, nous calculons le rapport F en divisant le carré moyen intergroupes par le carré moyen intra groupes :

\[ F = \frac{\text{MS}_{b}}{\text{MS}_{w}} \]

À un niveau très général, l’intuition derrière la statistique F est simple. Des valeurs plus grandes de F signifient que la variation inter groupes est importante par rapport à la variation intra groupes. Par conséquent, plus la valeur de F est élevée, plus nous avons de preuves contre l’hypothèse nulle. Mais quelle doit être la taille de F pour que H₀ soit réellement rejetée ? Pour répondre à cela, vous avez besoin d’une compréhension un peu plus profonde de ce qu’est l’ANOVA et de ce que sont réellement les valeurs des carrés moyens.

La section suivante l’aborde un peu plus en détail, mais pour les lecteurs qui ne sont pas intéressés par les détails de ce que le test mesure réellement, je vais aller droit au but. Afin de compléter notre test d’hypothèse, nous devons connaître la distribution d’échantillonnage pour F si l’hypothèse nulle est vraie. Il n’est pas surprenant que la distribution d’échantillonnage pour la statistique F sous l’hypothèse nulle soit une distribution F. Si vous vous souvenez de notre discussion sur la distribution F au chapitre 7, la distribution F a deux paramètres, correspondant aux deux degrés de liberté impliqués. Le premier df1 est le degré de liberté dfb (dfb) inter groupes, et le second df2 est le degré de liberté ddlw (dfw) intra groupes.

Tableau 13‑1 : Toutes les quantités clés d’une ANOVA organisée dans un tableau ANOVA “standard”. Les formules pour toutes les quantités (à l’exception de la valeur p qui a une formule très moche et qui serait cauchemardesquement difficile à calculer sans ordinateur) sont présentées.

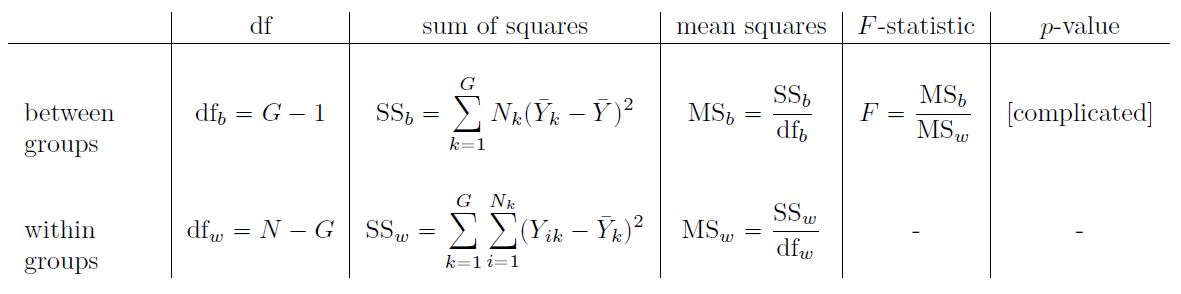
13.2.4 Le modèle pour les données et la signification de F

Au niveau fondamental, ANOVA est une compétition entre deux modèles statistiques différents, H₀ et H₁. Lorsque j’ai décrit les hypothèses nulle et alternative au début de la section, j’étais un peu imprécis quant à la nature réelle de ces modèles. Je vais y remédier maintenant, même si vous ne m’aimerez probablement pas pour cela. Si vous vous souvenez bien, notre hypothèse nulle était que toutes les moyennes de groupe sont identiques les unes aux autres. Si c’est le cas, alors une façon naturelle de penser à la variable de résultat Y_ik consiste à décrire les scores individuels en termes d’une seule moyenne de population \(\mu\), plus l’écart par rapport à cette moyenne de population. Cet écart est habituellement appelé \(\epsilon_{\text{ik}}\) et est traditionnellement appelé l’erreur ou le résidu associé à cette observation. Mais attention cependant. Tout comme nous l’avons vu avec le mot « significatif », le mot « erreur » a une signification technique en statistique qui n’est pas tout à fait la même que sa définition française courante. Dans le langage courant, « erreur » implique une erreur quelconque, mais ce n’est pas le cas dans les statistiques (ou du moins, pas nécessairement). Dans cet esprit, le mot « résiduel » est un meilleur terme que le mot « erreur ». En statistique, les deux mots signifient « variabilité résiduelle », c’est-à-dire « choses » que le modèle ne peut expliquer.

Quoi qu’il en soit, voici à quoi ressemble l’hypothèse nulle quand on l’écrit comme modèle statistique

\[ Y_{\text{ik}} = \mu + \epsilon_{\text{ik}} \]

où nous faisons l’hypothèse (discutée plus loin) que les valeurs résiduelles \(\epsilon_{\text{ik}}\) sont normalement distribuées, avec une moyenne 0 et un écart type \(\sigma\) qui est le même pour tous les groupes. Pour utiliser la notation que nous avons introduite au chapitre 7, nous écrivons cette hypothèse comme suit

\[ \epsilon_{\text{ik}}\sim Normal(0,\sigma^{2}) \]

Et l’hypothèse alternative, H₁ ? La seule différence entre l’hypothèse nulle et l’hypothèse alternative est que nous permettons à chaque groupe d’avoir une moyenne de population différente. Donc, si nous posons µ_k la moyenne de population pour le k-ème groupe dans notre expérience, alors le modèle statistique correspondant à H₁ est le suivant

\[ Y_{\text{ik}} = \mu_{k} + \epsilon_{\text{ik}} \]

où, encore une fois, nous supposons que les termes d’erreur sont normalement distribués avec une moyenne de 0 et un écart-type \(\sigma\). Autrement dit, l’hypothèse alternative suppose également que

\[ \epsilon\sim Normal(0,\sigma^{2}) \]

Bien, maintenant que nous avons décrit plus en détail les modèles statistiques qui sous-tendent H₀ et H₁, il est maintenant assez simple de dire ce que les carrés moyens mesurent, et ce que cela signifie pour l’interprétation de F. Je ne vous ennuierai pas avec la preuve, mais il s’avère que le carré moyen intragroupe, MS_w, peut être considéré comme un estimateur (au sens technique, chapitre 8) de la variance des erreurs \(\sigma^{2}\). La moyenne quadratique entre groupes MS_b est également un estimateur, mais ce qu’elle estime est la variance d’erreur plus une quantité qui dépend des différences réelles entre les moyennes du groupe. Si nous appelons cette quantité Q, alors nous pouvons voir que la statistique F est fondamentalement¹¹¹

\[ F = \frac{\hat{Q} + {\hat{\sigma}}^{2}}{{\hat{\sigma}}^{2}} \]

où la valeur vraie Q=0 si l’hypothèse nulle est vraie, et Q>0 si l’hypothèse alternative est vraie (par exemple, Hays 1994, ch. 10. Par conséquent, au minimum, la valeur de F doit être supérieure à 1 pour avoir une chance de rejeter l’hypothèse nulle. Notez que cela ne signifie pas qu’il est impossible d’obtenir une valeur F inférieure à 1, mais que si l’hypothèse nulle est vraie, la distribution d’échantillonnage du rapport F a une moyenne de 1¹¹², nous devons donc voir des valeurs F supérieures à 1 afin de rejeter la valeur nulle.

Pour être un peu plus précis au sujet de la distribution d’échantillonnage, notons que si l’hypothèse nulle est vraie, MSb et MSw sont tous deux des estimateurs de la variance des résidus \(\epsilon_{\text{ik}}\). Si ces résidus sont normalement distribués, vous pourriez soupçonner que l’estimation de la variance de \(\epsilon_{\text{ik}}\) suit une distribution de chi-carré, parce que (comme nous l’avons vu à la section 7.6) c’est ce qui caractérise une distribution du chi-carré. C’est ce qu’on obtient quand on fait la somme de plusieurs choses normalement distribuées. Et puisque la distribution F est (encore une fois, par définition) ce que vous obtenez lorsque vous prenez le rapport entre deux valeurs qui suivent une distribution de \(\chi^{2}\), nous avons notre distribution d’échantillonnage. Évidemment, je passe sous silence beaucoup de choses quand je dis cela, mais en termes généraux, c’est vraiment de là que vient notre distribution d’échantillonnage.

13.2.5 Un exemple travaillé

La discussion précédente était assez abstraite et un peu technique, alors je pense qu’à ce stade, il pourrait être utile de voir un exemple concret. Pour cela, revenons aux données sur les essais cliniques que j’ai présentées au début du chapitre. Les statistiques descriptives que nous avons calculées au début nous indiquent que notre groupe représente une amélioration moyenne de l’humeur de 0,45 pour le placebo, 0,72 pour Anxifree et 1,48 pour Joyzepam. Avec cela à l’esprit, faisons un jeu comme si nous étions en 1899¹¹³et commençons à faire quelques calculs au crayon et sur papier. Je ne le ferai que pour les 5 premières observations car nous ne sommes pas en 1899 et je suis très paresseux. Commençons par calculer SS_w, la somme des carrés au sein du groupe. D’abord, dressons un beau tableau pour nous aider dans nos calculs :

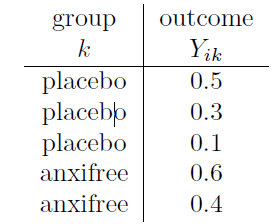
À ce stade, la seule chose que j’ai incluse dans le tableau, ce sont les données brutes elles-mêmes. C’est-à-dire la variable de regroupement (c.-à-d. drug) et la variable de résultat (c.-à-d. outcomes = mood.gain) pour chaque personne. Notez que la variable de résultat ici correspond à la valeur de Y~ik~ de notre équation précédente. L’étape suivante du calcul consiste à noter, pour chaque personne de l’étude, la moyenne du groupe correspondant,\({\bar{Y}}_{k}\). C’est un peu répétitif mais pas particulièrement difficile puisque nous avons déjà calculé les moyennes de ces groupes lors de la réalisation de nos statistiques descriptives :

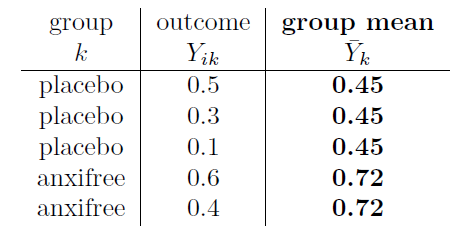
Maintenant que nous les avons notés, nous devons calculer, encore une fois pour chaque personne, l’écart par rapport à la moyenne du groupe correspondant. C’est-à-dire, nous voulons faire la soustraction \(Y_{\text{ik}} - {\bar{Y}}_{k}\). Après avoir fait ça, il faut tout ranger. Voilà ce qu’on obtient quand on fait ça :

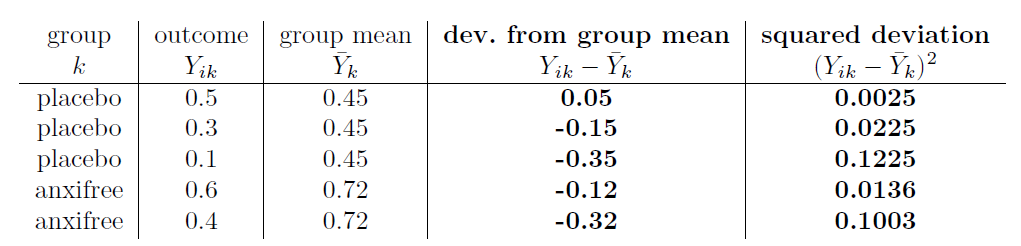
La dernière étape est tout aussi simple. Pour calculer la somme des carrés à l’intérieur d’un groupe, nous additionnons simplement les écarts au carré de toutes les observations :

\[\begin{aligned} \text{SS}_{w} &= 0,0025 + 0,0225 + 0,1225 + 0,0136 + 0,1003\\ &= 0,2614 \end{aligned} \]

Bien sûr, si nous voulions vraiment obtenir la bonne réponse, nous devrions le faire pour les 18 observations de l’ensemble des données, pas seulement pour les cinq premières. Nous pourrions continuer les calculs au crayon et au papier si nous le voulions, mais c’est assez fastidieux. Sinon, il n’est pas trop difficile de le faire dans un tableur dédié tel qu’OpenOffice ou Excel. Essayez de le faire vous-même. Celui que j’ai fait, dans Excel, est dans le fichier clinicaltrial_anova.xls. Lorsque vous le faites, vous devriez obtenir une somme intra-groupe de carrés de 1,39.

Bien. Maintenant que nous avons calculé la variation à l’intérieur des groupes, SSw, il est temps concentrer vers la somme des carrés entre groupes, SSb. Les calculs pour ce cas sont très similaires. La principale différence est qu’au lieu de calculer les différences entre une observation Y_ik et une moyenne de groupe \({\bar{Y}}_{k}\) pour toutes les observations, nous calculons les différences entre la moyenne de groupe \({\bar{Y}}_{k}\) et la moyenne générale \(\bar{Y}\) (dans ce cas 0,88) pour tous les groupes.

Cependant, pour les calculs entre les groupes, nous devons multiplier chacun de ces écarts au carré par Nk, le nombre d’observations dans le groupe. Nous le faisons parce que chaque observation dans le groupe (tous les N_k d’entre eux) est associée à une différence entre les groupes. Donc, s’il y a six personnes dans le groupe placebo et que la moyenne du groupe placebo diffère de la moyenne générale de 0,19, alors la variation totale inter groupes associée à ces six personnes est 6 x 0,19=1.14. Nous devons donc étendre notre petit tableau de calculs :

Ainsi, la somme des carrés inter groupes est obtenue en additionnant ces « écarts quadratiques pondérés » sur les trois groupes de l’étude :

\[\begin{aligned} \text{SS}_{b} &= 1,14 + 0,18 + 2,16\\ &= 3,48 \end{aligned} \]

Comme vous pouvez le voir, les calculs entre les groupes sont beaucoup plus courts¹¹⁴. Maintenant que nous avons calculé nos sommes de valeurs des carrés SSb et SSw, le reste de l’ANOVA est assez indolore. L’étape suivante consiste à calculer les degrés de liberté. Puisque nous avons G = 3 groupes et N = 18 observations au total, nos degrés de liberté peuvent être calculés par simple soustraction :

\[\begin{aligned} \text{ddl}_{b} &= G - 1 = 2\\ \text{ddl}_{w} &= N - G = 15 \end{aligned} \]

Ensuite, puisque nous avons maintenant calculé les valeurs des sommes des carrés et des degrés de liberté, tant pour la variabilité intra groupes que pour la variabilité inter groupes, nous pouvons obtenir les carrés moyens en divisant l’une par l’autre :

\[\begin{aligned} \text{MS}_{b} = \frac{\text{SS}_{b}}{\text{ddl}_{b}} = \frac{3,48}{2} = 1,74\\ {\text{MS}_{w} = \frac{\text{SS}_{w}}{\text{ddl}_{w}} = \frac{1,39}{15} = 0,09} \end{aligned} \]

On a presque fini. Les carrés moyens peuvent être utilisés pour calculer la valeur F, qui est la statistique du test qui nous intéresse. Pour ce faire, nous divisons la valeur MS inter groupes par la valeur MS à intra groupes.

\[ F = \frac{\text{MS}_{b}}{\text{MS}_{w}} = \frac{1,74}{0,09} = 19,3 \]

Wouahou ! C’est terriblement excitant, non ? Maintenant que nous disposons de nos statistiques de test, la dernière étape consiste à déterminer si le test lui-même nous donne un résultat significatif. Comme nous l’avons vu au chapitre 9 autrefois, ce que nous ferions est d’ouvrir un manuel de statistiques ou de feuilleter l’annexe qui aurait en fait une énorme table de valeurs et nous trouverions la valeur seuil F correspondant à une valeur particulière d’alpha (la région de rejet d’hypothèse nulle), par exemple .05, .01 ou .001, pour 2 et 15 degrés de liberté. En procédant de cette façon, nous obtiendrions une valeur seuil F pour un alpha de .001 de 11,34. Comme cette valeur est inférieure à notre valeur F calculée, nous disons que p<.001. Mais c’était le bon vieux temps, et de nos jours le logiciel de statistiques sophistiqué calcule la valeur p exacte pour vous. En fait, la valeur p exacte est 0,000071. Donc, à moins que nous ne soyons extrêmement prudents quant à notre taux d’erreur de type I, nous sommes pratiquement certains de pouvoir rejeter l’hypothèse nulle.

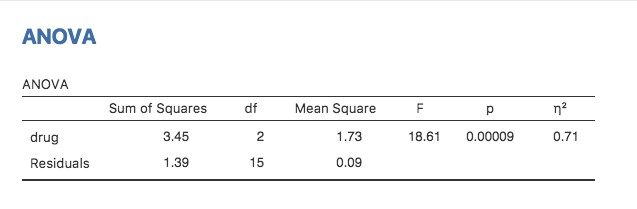
C’est presque fini. Une fois nos calculs terminés, il est de tradition d’organiser tous ces chiffres dans un tableau ANOVA comme celui du Tableau 13‑1. Pour les données de nos essais cliniques, le tableau ANOVA ressemblerait à ceci :

De nos jours, vous n’aurez probablement jamais beaucoup de d’occasion de vouloir construire un de ces tableaux vous-même, mais vous constaterez que presque tous les logiciels statistiques (Jamovi inclus) ont tendance à organiser la sortie d’une ANOVA dans un tableau comme celui-ci, donc c’est une bonne idée de s’habituer à les lire. Cependant, bien que le logiciel produise un tableau d’ANOVA complète, il n’y a presque jamais une bonne raison d’inclure le tableau entier dans votre rédaction. Une façon assez standard de rapporter ce résultat serait d’écrire quelque chose comme ceci :

L’ANOVA à un facteur a montré un effet significatif du médicament sur l’amélioration de l’humeur (F(2,15)=19,3,p<.001).

Soupir ! Tant de travail pour une courte phrase.

13.3 Exécuter une ANOVA dans Jamovi

Je suis presque sûr que je sais ce que vous pensez après avoir lu la dernière section, surtout si vous avez suivi mes conseils et que vous avez fait tout cela vous-même au crayon et sur papier (c.-à-d. dans un tableur). Faire les calculs d’ANOVA soi-même, c’est nul. Il y a beaucoup de calculs à faire en cours de route, et il serait fastidieux de devoir le faire encore et encore chaque fois que vous voulez faire une analyse de variance.

13.3.1 Utiliser Jamovi pour spécifier votre ANOVA

Pour vous faciliter la vie, Jamovi peut faire une ANOVA…hourra ! Sélectionnez à l’analyse « ANOVA » -« ANOVA », et déplacez la variable mood.gain pour qu’elle se trouve dans la case « Dependent Variable», puis déplacez la variable drug pour qu’elle soit dans la case « Fixed Factors ». Ceci devrait donner les résultats comme le montre la Figure 13‑3.¹¹⁵ Notez que j’ai également coché la case \(\eta^{2}\), prononcée « eta » au carré, sous l’option « Effect Size » et ceci est également indiqué dans le tableau des résultats. Nous reviendrons sur les tailles d’effet un peu plus tard.

Figure 13‑3 : Tableau des résultats de Jamovi pour l’analyse de variance de l’humeur selon le médicament administré

Le tableau des résultats de Jamovi vous montre la somme des valeurs des carrés, les degrés de liberté, et d’autres quantités qui ne nous intéressent pas vraiment pour le moment. Notez, cependant, que Jamovi n’utilise pas les appellations inter groupe (between-group) et intra groupe (within-group). Au lieu de cela, il essaie d’attribuer des noms plus significatifs. Dans notre exemple particulier, la variance entre les groupes correspond à l’effet que le facteur drug a sur la variable de résultat, et la variance à l’intérieur des groupes correspond à la variabilité « résiduelle », c’est-à-dire la variance résiduelle. Si nous comparons ces chiffres à ceux que j’ai calculés à la main à la section 13.2.5, vous pouvez voir que ce sont plus ou moins les mêmes, abstraction faite des erreurs d’arrondi. La somme des carrés entre les groupes est SSb = 3,45, la somme des carrés au sein des groupes est SS_w= 1,39, et les degrés de liberté sont respectivement 2 et 15. Nous obtenons aussi la valeur F et la valeur p et, encore une fois, elles sont plus ou moins les mêmes, avec des erreurs d’arrondis par rapport aux chiffres que nous avons calculés nous-mêmes en faisant cela de manière longue et fastidieuse.

13.4 Taille de l’effet

Il y a différentes façons de mesurer la taille de l’effet dans une ANOVA, mais les mesures les plus couramment utilisées sont \(\eta^{2}\) (eta au carré) et \(\eta^{2}\) partiel. Pour une analyse de la variance à un facteur, ils sont identiques l’un à l’autre, alors pour le moment, je vais simplement expliquer \(\eta^{2}\). La définition de \(\eta^{2}\) est en fait très simple.

\[ \eta^{2} = \frac{\text{SS}_{b}}{\text{SS}_{\text{tot}}} \]

Il ne s’agit que de ça. Ainsi, quand je regarde le tableau d’ANOVA de la Figure 13‑3, je vois que SS_b = 3,45 et SS_tot = 3,45 + 1,39 = 4,84. Nous obtenons alors une valeu \(\eta^{2}\) de

\[ \eta^{2} = \frac{3,45}{4,84} = 0,71 \]

L’interprétation de \(\eta^{2}\) est tout aussi simple. Il s’agit de la proportion de la variabilité de la variable résultat (mood.gain) qui peut s’expliquer par le prédicteur (drug). Une valeur de \(\eta^{2}\) = 0 signifie qu’il n’y a aucune relation entre les deux, alors qu’une valeur de \(\eta^{2}\) = 1 signifie que la relation est parfaite. Mieux encore, la valeur de \(\eta^{2}\) est très étroitement liée à R², comme nous l’avons vu à la section 12.6, et a une interprétation équivalente.

Bien que de nombreux manuels de statistiques suggèrent \(\eta^{2}\) comme mesure par défaut de la taille de l’effet dans ANOVA, il y a un article intéressant de Daniel Lakens sur un blog qui suggère que l’eta-carré n’est peut-être pas la meilleure mesure de l’ampleur de l’effet dans le monde réel, car il peut être un estimateur biaisé¹¹⁶. Il est utile de noter qu’il existe également une option dans Jamovi pour spécifier omega-squared (\(\omega^{2}\)), qui est moins biaisée, comparé à eta-carré.

13.5 Comparaisons multiples et tests post hoc

Chaque fois que vous exécutez une analyse de variance avec plus de deux groupes et que vous vous retrouvez avec un effet significatif, la première chose que vous voudrez probablement demander est quels groupes sont réellement différents les uns des autres. Dans notre exemple de médicaments, notre hypothèse nulle était que les trois médicaments (placebo, Anxifree et Joyzepam) ont exactement le même effet sur l’humeur. Mais si vous y réfléchissez bien, l’hypothèse nulle est en fait de prétendre trois choses différentes à la fois. Plus précisément, il prétend que :

• Le médicament de votre concurrent (Anxifree) ne vaut pas mieux qu’un placebo (c.-à-d. \(\mu_{A}=\mu_{P}\))
• Votre médicament (Joyzepam) ne vaut pas mieux qu’un placebo (c.-à-d.\(\mu_{J}=\mu_{P}\))
• Anxifree et Joyzepam sont également efficaces (c.-à-d. \(\mu_{J}=\mu_{A}\))

Si l’une de ces trois affirmations est fausse, alors l’hypothèse nulle est également fausse. Donc, maintenant que nous avons rejeté notre hypothèse nulle, nous pensons qu’au moins une de ces choses n’est pas vraie. Mais lesquelles ? Ces trois propositions sont toutes trois intéressantes. Puisque vous voulez certainement savoir si votre nouveau médicament Joyzepam est meilleur qu’un placebo, il serait bien de savoir comment il se compare à une alternative commerciale existante (c.-à-d., Anxifree). Il serait même utile de vérifier la performance d’Anxifree par rapport au placebo. Même si Anxifree a déjà été testé à fond contre placebo par d’autres chercheurs, il peut quand même être très utile de vérifier que votre étude produit des résultats similaires à ceux des travaux antérieurs.

Lorsque nous caractérisons l’hypothèse nulle en fonction de ces trois propositions distinctes, il apparaît clairement qu’il y a huit « états du monde « possibles qu’il faut distinguer :

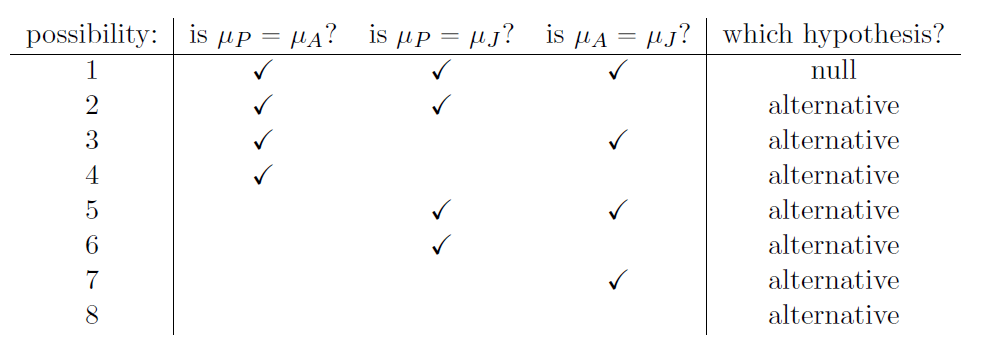
En rejetant l’hypothèse nulle, nous avons décidé que nous ne croyons pas que le #1 est le véritable état du monde. La prochaine question à se poser est la suivante : laquelle des sept autres possibilités nous semble la bonne ? Face à cette situation, il est généralement utile d’examiner les données. Par exemple, si nous examinons les graphiques de la Figure 13‑1, il est tentant de conclure que le Joyzepam est meilleur que le placebo et meilleur qu’Anxifree, mais il n’y a pas de différence réelle entre Anxifree et le placebo. Cependant, si nous voulons obtenir une réponse plus claire à ce sujet, il pourrait être utile d’effectuer quelques tests.

13.5.1 Exécution de tests t par paire

Comment pourrions-nous résoudre notre problème ? Étant donné que nous avons trois paires distinctes de moyennes (placebo contre Anxifree, placebo contre Joyzepam et Anxifree contre Joyzepam) à comparer, nous pourrions faire trois tests t distincts et voir ce qui se passe. C’est facile à faire en Jamovi. Allez dans les options de l’ANOVA « Post-hoc Tests », déplacez la variable drug dans la case active sur la droite, puis cliquez sur la case « No correction ». On obtiendra ainsi un tableau clair montrant toutes les comparaisons du test t par paires entre les trois niveaux de la variable du médicament, comme le montre la Figure 13‑4.

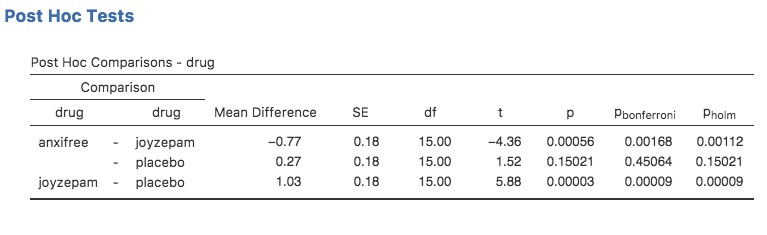
Figure 13‑4 : Tests t par pairs non corrigés comme comparaisons post hoc dans Jamovi

13.5.2 Corrections pour tests multiples

Dans la section précédente, j’ai laissé entendre qu’il y a un problème avec le fait de ne faire que des tas et des tas de tests t. Ce qui nous préoccupe, c’est que ce que nous faisons en effectuant ces analyses, c’est une « expédition de pêche ». Nous effectuons de nombreux tests sans trop d’orientation théorique, dans l’espoir que certains d’entre eux soient significatifs. Ce type de recherche sans théorie des différences de groupe qui est appelé analyse post hoc (« post hoc » en latin pour « à la suite de cela »).¹¹⁷

Il n’y a pas de mal à faire des analyses post hoc, mais il faut faire preuve de beaucoup de prudence. Par exemple, l’analyse que j’ai effectuée dans la section précédente devrait être évitée, car chaque test t individuel est conçu pour avoir un taux d’erreur de type I de 5 % (c.-à-d. \(\alpha =.05\)) et j’ai effectué trois de ces tests. Imaginez ce qui se serait passé si mon ANOVA avait impliqué 10 groupes différents, et que j’avais décidé de faire 45 tests t « post hoc » pour essayer de savoir lesquels étaient significativement différents les uns des autres, vous vous attendriez à ce que 2 ou 3 d’entre eux soient significatifs par hasard seulement. Comme nous l’avons vu au chapitre 9, le principe d’organisation central derrière les tests d’hypothèse nulle est que nous cherchons à contrôler notre taux d’erreur de type I, mais lorsque que j’exécute beaucoup de tests t à la fois afin de déterminer la source de mes résultats ANOVA, mon taux d’erreur réel de type I dans toute cette famille de tests est devenu complètement hors de contrôle.

La solution habituelle à ce problème est d’introduire un ajustement de la valeur p, qui vise à contrôler le taux d’erreur total dans la famille des tests (voir Shaffer, (1995)). Un ajustement de cette forme, qui est habituellement (mais pas toujours) appliqué lorsqu’on qu’on fait une analyse post hoc, est souvent appelé une correction pour des comparaisons multiples, bien qu’on l’appelle parfois « inférence simultanée ». Quoi qu’il en soit, il existe plusieurs façons différentes de procéder à cet ajustement. J’en aborderai quelques-unes dans cette section et dans la section 14.8, mais vous devez savoir qu’il existe de nombreuses autres méthodes (voir, par exemple, Hsu, (1996)).

13.5.3 Corrections de Bonferroni

Le plus simple de ces ajustements s’appelle la correction de Bonferroni (Dunn 1961), et c’est très simple. Supposons que mon analyse post hoc consiste en m tests séparés, et que je veux m’assurer que la probabilité totale de faire des erreurs de type I est tout au plus \(\alpha\)¹¹⁸. Dans ce cas, la correction de Bonferroni dit simplement « multiplier toutes vos valeurs p brutes par m ». Si p indique la valeur originale de p, et si \(p_{j}^{'}\) est la valeur corrigée, alors la correction de Bonferroni indique cela :

\[ p_{j}^{'} = m \times p \]

Ainsi, si vous utilisez la correction de Bonferroni, vous rejetteriez l’hypothèse nulle si \(p’< \alpha\). La logique derrière cette correction est très simple. Nous faisons m tests différents, donc si nous l’organisons de telle sorte que chaque test ait un taux d’erreur de Type I d’au plus \(\alpha /m\), alors le taux d’erreur de Type I total de ces tests ne peut pas être supérieur à \(\alpha\). C’est assez simple, à tel point que dans le document original, l’auteur écrit,

« La méthode donnée ici est si simple et si générale que je suis sûr qu’elle a dû être utilisée avant cela. Cependant, je ne la trouve pas et je ne peux donc que conclure que sa simplicité a peut-être empêché les statisticiens de se rendre compte qu’il s’agit d’une très bonne méthode dans certaines situations » (Dunn, (1961), p. 52-53).

Pour utiliser la correction de Bonferroni dans Jamovi, il suffit de cliquer sur la case à cocher « Bonferroni » dans les options « Correction », et vous verrez une autre colonne ajoutée au tableau des résultats ANOVA montrant les valeurs de p ajustées avec la correction de Bonferroni (Figure 13‑4). Si nous comparons ces troi valeurs p à celles des tests t non corrigés par paires, il est clair que la seule chose que Jamovi a faite est de les multiplier par 3.

13.5.4 Corrections de Holm

Bien que la correction de Bonferroni soit l’ajustement le plus simple, ce n’est généralement pas le meilleur à utiliser. Une méthode qui est souvent utilisée à la place est la correction de Holm (Holm 1979). L’idée derrière la correction Holm est de prétendre que vous faites les tests séquentiellement, en commençant par la plus petite valeur de p (brute) et en passant à la plus grande. Pour la j-ème plus grande des valeurs de p, l’ajustement est soit

\[ p_{j}^{'} = j \times p_{j} \]

(c.-à-d. que la valeur de p la plus élevée reste inchangée, la deuxième valeur de p* la plus élevée est doublée, la troisième valeur de p la* plus élevée est triplée, et ainsi de suite), ou

\[ p_{j}^{'} = p_{j + 1}^{'} \]

le plus élevé des deux. Cela peut sembler un peu déroutant, alors passons les choses en revue un peu plus lentement. Voici ce que fait la correction Holm. Tout d’abord, vous triez toutes vos valeurs p dans l’ordre, de la plus petite à la plus grande. Pour la plus petite valeur p, il suffit de la multiplier par m, et c’est terminé. Cependant, pour tous les autres, il s’agit d’un processus en deux étapes. Par exemple, lorsque vous passez à la deuxième plus petite valeur p, vous la multipliez d’abord par m-1. Si cela produit un nombre plus grand que la valeur p ajustée que vous avez obtenue la dernière fois, alors vous le gardez. Mais si elle est plus petite que la dernière, alors vous copiez la dernière valeur de p. Pour illustrer comment cela fonctionne, considérons le tableau ci-dessous, qui montre les calculs d’une correction Holm pour une collection de cinq valeurs p :

J’espère que cela clarifie les choses.

Bien qu’elle soit un peu plus difficile à calculer, la correction de Holm a de très bonnes propriétés. Il est plus puissant que Bonferroni (c.-à-d. qu’il a un taux d’erreur de type II plus faible) mais, aussi contre-intuitif que cela puisse paraître, il a le même taux d’erreur de type I. Par conséquent, en pratique, il n’y a jamais de raison d’utiliser la correction de Bonferroni plus simple puisqu’elle est toujours surpassée par la correction de Holm légèrement plus élaborée. Pour cette raison, la correction de Holm devrait vous permettre d’accéder à la correction des comparaisons multiples. La Figure 13‑4 montre également les valeurs p corrigées de Holm et, comme vous pouvez le voir, la plus grande valeur* p* (correspondant à la comparaison entre Anxifree et le placebo) n’est pas modifiée. Avec une valeur de .15, c’est exactement la même valeur que celle que nous avons obtenue à l’origine lorsque nous n’avons appliqué aucune correction du tout. Par contre, la plus petite valeur p (Joyzepam contre placebo) a été multipliée par trois.

13.5.5 Rédaction du test post hoc

Enfin, après avoir effectué l’analyse post hoc pour déterminer quels groupes sont significativement différents les uns des autres, vous pouvez écrire le résultat comme ceci :

Des tests post hoc (utilisant la correction Holm pour ajuster p) ont indiqué que Joyzepam produisait un changement d’humeur significativement plus important que Anxifree (p =.001) et le placebo (\(p=9,0 \times 10^{-5}\)). Nous n’avons trouvé aucune preuve qu’Anxifree ait donné de meilleurs résultats que le placebo (p=.15).

Ou, si vous n’aimez pas l’idée de rapporter des valeurs p exactes, alors vous changeriez ces chiffres pour p<.01, p<.001 et p<.05 respectivement. Quoi qu’il en soit, l’essentiel est que vous indiquiez que vous avez utilisé la correction de Holm pour ajuster les valeurs p. Et bien sûr, je suppose qu’ailleurs dans le rapport, vous avez inclus les statistiques descriptives pertinentes (c.-à-d. les moyennes et les écarts-types des groupes), puisque ces valeurs p ne sont pas très informatives en soi.

13.6 Hypothèses de l’ANOVA à un facteur

Comme tout test statistique, l’analyse de la variance repose sur certaines hypothèses concernant les données, en particulier les résidus. Il y a trois hypothèses clés que vous devez connaître : la normalité, l’homogénéité de la variance et l’indépendance.

Si vous vous souvenez de la section 13.2.4, que j’espère que vous avez au moins survolé même si vous n’avez pas tout lu, j’ai décrit les modèles statistiques qui sous-tendent ANOVA de cette façon :

\[\begin{aligned} H_{0}:\ \ \ &Y_{\text{ik}} = \mu + \epsilon_{\text{ik}}\\ H_{1} :\ \ \ &Y_{\text{ik}} = \mu_{k} + \epsilon_{\text{ik}} \end{aligned} \]

Dans ces équations, \(\mu\) fait référence à une seule moyenne de la population qui est la même pour tous les groupes, et \(\mu_{k}\) est la moyenne de population pour le k-ème groupe. Jusqu’à présent, nous nous sommes surtout intéressés à savoir si nos données sont mieux décrites par la moyenne de la population (l’hypothèse nulle) ou par les différentes moyennes propres à chaque groupe (l’hypothèse alternative). C’est logique, bien sûr, car c’est en fait la question de recherche importante ! Toutefois, toutes nos méthodes de vérification se sont implicitement appuyées sur une hypothèse précise au sujet des résidus, \(\epsilon_{\text{ik}}\) à savoir que

\[ \epsilon_{\text{ik}}\sim Normal(0,\sigma^{2}) \]

Aucune des formules ne fonctionne correctement sans ce présupposé. Ou, pour être précis, vous pouvez toujours faire tous les calculs et vous obtiendrez une statistique F, mais vous n’avez aucune garantie que cette statistique F mesure réellement ce que vous pensez qu’elle mesure, et donc toute conclusion que vous pourriez tirer sur la base du test F pourrait être fausse.

Alors, comment vérifier si l’hypothèse sur les résidus est exacte ? Eh bien, comme je l’ai indiqué plus haut, il y a trois hypothèses distinctes cachées dans cee seul présupposé, et nous les examinerons séparément.

• Homogénéité de la variance. Notez que nous n’avons qu’une seule valeur pour l’écart-type de la population (c.-à-d. \(\sigma\)), plutôt que de permettre à chaque groupe d’avoir sa propre valeur (c.-à-d. \(\sigma_{k}\)). C’est ce qu’on appelle l’hypothèse d’homogénéité de la variance (parfois appelée homoscédasticité). L’analyse de variance suppose que l’écart-type de la population est le même pour tous les groupes. Nous en parlerons en détail à la section 13.6.1.

• Normalité. On suppose que les résidus sont normalement répartis. Comme nous l’avons vu à la section 11.8, nous pouvons l’évaluer en examinant les graphiques QQ (ou en effectuant un test Shapiro-Wilk). J’en parlerai davantage dans le contexte de l’analyse de variance à la section 13.6.4.

• Indépendance. L’hypothèse d’indépendance est un peu plus délicate. Ce que cela signifie essentiellement, c’est que le fait de connaître un résidu ne vous dit rien au sujet d’un autre résidu. Toutes les valeurs \(\epsilon_{\text{ik}}\) sont supposées avoir été générées sans « égard » ou « relation » avec les autres. Il n’y a pas de façon évidente ou simple de tester cela, mais il y a certaines situations qui constituent des violations évidentes de cette règle. Par exemple, si vous avez un modèle à mesures répétées, où chaque participant à votre étude apparaît dans plus d’une condition, alors l’indépendance ne tient pas. Il y a une relation particulière entre certaines observations, à savoir celles qui correspondent à la même personne ! Lorsque cela se produit, vous devez utiliser l’ANOVA pour mesures répétées (voir Section 13.8).

13.6.1 Vérification de l’hypothèse d’homogénéité de la variance

Faire le test préliminaire sur les variances, c’est un peu comme prendre la mer à la rame pour savoir si les conditions sont suffisamment calmes pour qu’un paquebot quitte le port ! /- George Box (Box 1953)

Il y a plus d’une façon de dépecer un chat, comme on dit, et plus d’une façon de vérifier l’hypothèse d’homogénéité des variance (bien que, pour une raison inconnue, personne n’en ait parlé). Le test de Levene (Levene 1960) et le test de Brown-Forsythe (Brown and Forsythe 1974) sont les tests les plus couramment utilisés dans la littérature pour cela.

Que vous fassiez le test de Levene standard ou le test de Brown-Forsythe, la statistique du test, qui est parfois désignée par F, mais parfois aussi par W, est calculée exactement de la même manière que la statistique F de l’analyse de variance standard, en utilisant simplement un Z_ik plutôt qu’un Y_ik. En ayant cela à l’esprit, nous pouvons continuer à examiner comment faire le test avec Jamovi.

Le test de Levene est incroyablement simple. Supposons que nous ayons notre variable de résultat Yik. Tout ce que nous faisons est de définir une nouvelle variable, que j’appellerai Z_ik, correspondant à l’écart absolu par rapport à la moyenne du groupe

\[ Z_{\text{ik}} = \left | Y_{\text{ik}} - {\bar{Y}}_{k} \right | \]

Bien, à quoi cela nous sert-il ? Prenons un moment pour réfléchir à ce qu’est réellement Z_ik et à ce que nous essayons de tester. La valeur de Z_ik est une mesure de la façon dont la i-ème observation dans le k-ème groupe s’écarte de sa moyenne de groupe. Et notre hypothèse nulle est que tous les groupes ont la même variance, c’est-à-dire les mêmes écarts globaux par rapport aux moyennes du groupe ! Ainsi, l’hypothèse nulle dans un test de Levene est que les moyennes de Z de la population sont identiques pour tous les groupes. Bien. Nous avons donc besoin maintenant d’un test statistique de l’hypothèse nulle que toutes les moyennes des groupes sont identiques. Où l’avons-nous déjà vu ? Ah oui, c’est l’ANOVA, et donc tout ce que fait le test de Levene, c’est d’exécuter une ANOVA sur la nouvelle variable Z_ik.

Et le test Brown-Forsythe ? Est-ce que cela fait quelque chose de particulièrement différent ? Non. Le seul changement par rapport au test de Levene est qu’il construit la variable transformée Z d’une manière légèrement différente, en utilisant des écarts par rapport aux médianes du groupe plutôt que des écarts par rapport aux moyennes du groupe. C’est-à-dire que nous avons, pour le test Brown-Forsythe

\[ Z_{\text{ik}} = \left| Y_{\text{ik}} - \text{median}_{k}(Y) \right| \]

où médian_k(Y)est la médiane pour le groupe k.

13.6.2 Exécuter le test Levene dans Jamovi

Bien, alors comment fait-on le test Levene ? C’est très simple - sous l’option d’ANOVA « Assumption Checks », cliquez simplement sur la case à cocher « Homogeneity tests ». En regardant le résultat à la Figure 13‑5, on constate que le test est non significatif (\(F(2,15)=1,45, p =.266\)), il semble donc que l’hypothèse d’homogénéité de la variance soit bonne. Cependant, les apparences peuvent être trompeuses ! Si la taille de votre échantillon est assez grande, alors le test de Levene pourrait avoir un effet significatif (c.-à-d. p < .05) même si l’hypothèse d’homogénéité de la variance n’est pas trangressée ce qui peut nuire à la robustesse de l’ANOVA. C’est ce que George Box faisait valoir dans la citation ci-dessus. De même, si la taille de votre échantillon est assez petite, l’hypothèse d’homogénéité de la variance pourrait ne pas être satisfaite et pourtant un test de Levene pourrait être non significatif (c.-à-d. p > .05). Cela signifie que, parallèlement à tout test statistique de cette d’hypothèse vérifiée, vous devez toujours tracer l’écart-type pour chaque groupe ou catégorie de l’analyse… juste pour voir si elles sont assez semblables (c.-à-d. homogénéité de la variance) ou non.

Figure 13‑5 : Sortie de test Levene pour ANOVA unidirectionnelle in Jamovi

13.6.3 Vérification de l’hypothèse d’homogénéité des variances

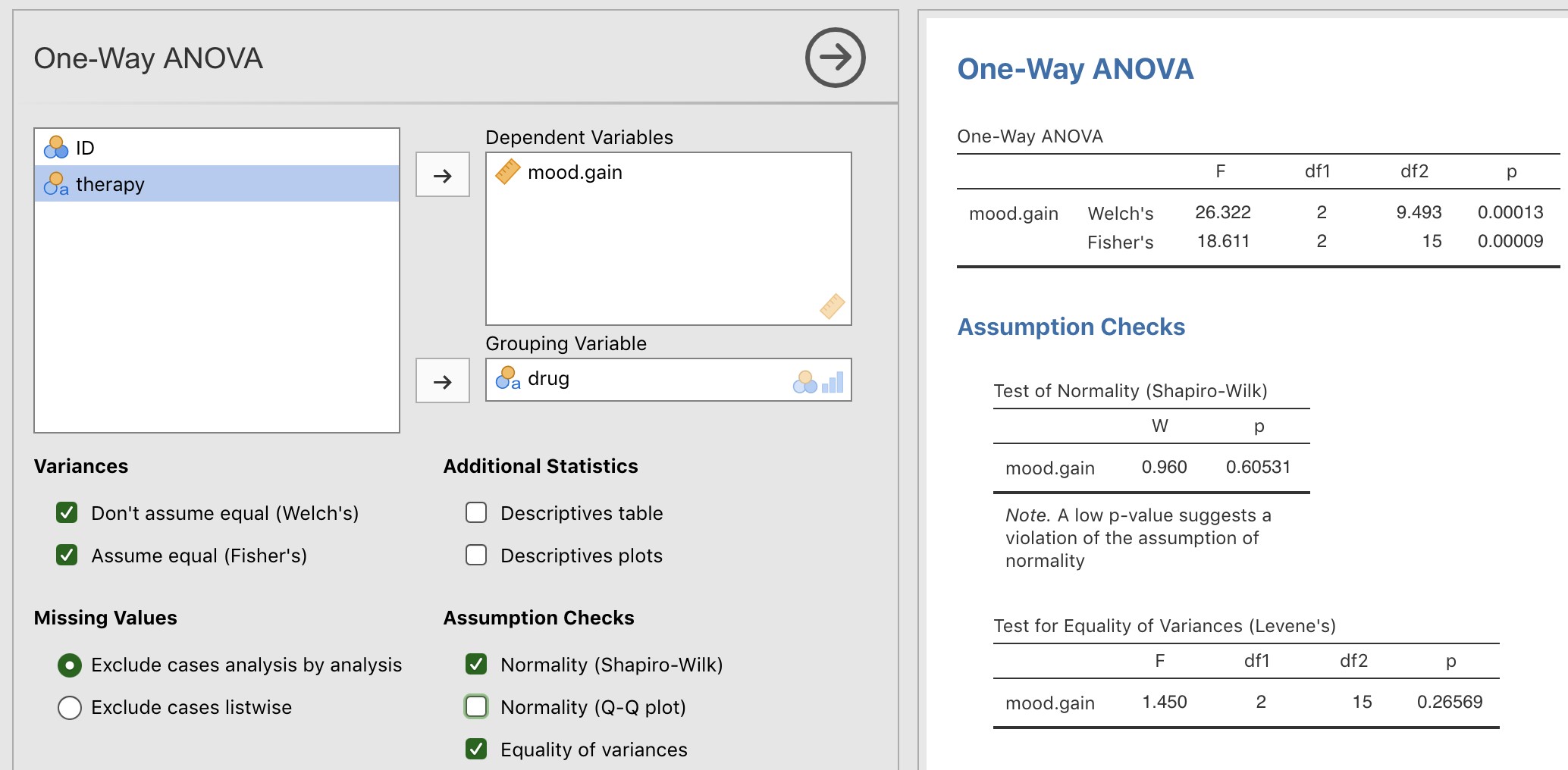
Dans notre exemple, l’hypothèse d’homogénéité des variances s’est révélée assez sûre : le test de Levene s’est avéré non significatif (même si nous devrions aussi examiner le graphique des écarts-types), nous n’avons donc probablement pas à nous inquiéter. Cependant, dans la vraie vie, nous n’avons pas toujours cette chance. Comment sauver notre analyse de variance lorsque l’hypothèse d’homogénéité des variances n’est pas respectée ? Si vous vous souvenez de notre discussion sur les tests t, nous avons déjà vu ce problème auparavant. Le test t de Student suppose des variances égales, la solution consistait à utiliser le test t de Welch, si ce n’était pas le cas. En fait, Welch (1951) a également montré comment nous pouvons résoudre ce problème pour l’ANOVA aussi (le test univarié de Welch). Il est implémenté dans Jamovi dans « ANOVA One Way ». Il s’agit d’une approche d’analyse spécifique pour une analyse ANOVA à un facteur, et pour exécuter l’analyse ANOVA à un facteur de Welch pour notre exemple, nous réexécuterions l’analyse comme précédemment, mais cette fois en utilisant la commande Jamovi « ANOVA One Way » analysis, et cocherions l’option pour le test de Welch (voir Figure 13‑6).

Figure 13‑6 : Le test de Welch dans le cadre de l’analyse ANOVA à un facteur avec Jamovi

Pour comprendre ce qui se passe ici, comparons ces chiffres à ce que nous avons obtenu plus tôt dans la section 13.3 lorsque nous avons lancé notre analyse de variance initiale. Pour t’éviter d’avoir à te retourner, voilà ce qu’on a eu la dernière fois : \(F(2,15)=18.611, p = .00009\), également présenté comme le test de Fisher dans l’analyse de variance à un facteur présentée à la Figure 13‑6.

Bien, au départ notre ANOVA nous a donné le résultat F(2,15)=18,6, alors que le test univarié de Welch nous a donné F(2, 9,49)=26,32. En d’autres termes, le test de Welch a réduit les degrés de liberté au sein des groupes de 15 à 9,49 et la valeur F est passée de 18,6 à 26,32.

13.6.4 Vérification de l’hypothèse de normalité

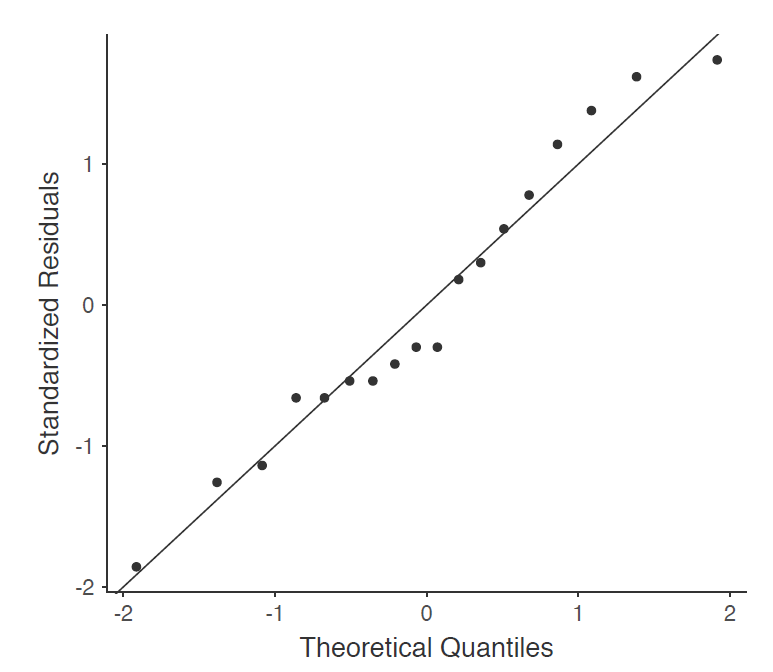
Il est relativement simple de tester l’hypothèse de normalité. Nous avons couvert la plupart de ce que vous devez savoir à la section 11.8. La seule chose que nous avons vraiment besoin de faire est de dessiner un tracé QQ et, en plus, s’il est disponible, de faire le test Shapiro-Wilk. Le tracé QQ est illustré à la Figure 13‑7 me semble assez normal. Si le test de Shapiro-Wilk n’est pas significatif (c.-à-d.> .05), cela signifie que l’hypothèse de normalité n’est pas violée. Toutefois, comme dans le cas du test de Levene, si la taille de l’échantillon est importante, un test Shapiro-Wilk significatif peut être un faux positif, où l’hypothèse de normalité n’est pas violée de manière importante pour l’analyse. De même, un très petit échantillon peut produire de faux négatifs. C’est pourquoi une inspection visuelle du graphique QQ est importante.

Figure 13‑7 : Graphique QQ produit à partir des options de l’ANOVA à un facteur de Jamovi

En plus de l’inspection du graphique QQ pour détecter tout écart par rapport à la normale, le test Shapiro-Wilk pour nos données montre un effet non significatif, avec p=.6053 (voir Figure 13‑6). Cela confirme donc l’analyse du graphique QQ ; les deux contrôles n’indiquent pas que l’hypothèse normalité a été violée.

13.7 Suppression de l’hypothèse de normalité

Maintenant que nous avons vu comment vérifier la normalité, nous sommes naturellement amenés à nous demander ce que nous pouvons faire pour remédier aux violations de la normalité. Dans le contexte d’une analyse de variance à un facteur, la solution la plus simple est probablement de passer à un test non paramétrique (c.-à-d. un test qui ne repose sur aucune hypothèse particulière quant au type de distribution en cause). Nous avons déjà vu des tests non paramétriques au chapitre 11. Lorsque vous n’avez que deux groupes, le test de Mann-Whitney ou le test de Wilcoxon fournissent l’alternative non paramétrique dont vous avez besoin. Lorsque vous avez trois groupes ou plus, vous pouvez utiliser le test de la somme de rang Kruskal-Wallis (Kruskal and Wallis 1952). C’est le test dont nous parlerons plus tard.

13.7.1 La logique derrière le test Kruskal-Wallis

Le test Kruskal-Wallis est étonnamment similaire à l’ANOVA, à certains égards. Dans l’ANOVA, nous avons commencé par Y_ik, la valeur de la variable de résultat pour la ième personne du groupe k. Pour le test Kruskal Wallis, nous classerons toutes ces valeurs Y_ik et effectuerons notre analyse sur les données classées.

Posons que R_ik désigne le classement donné au ième membre du k-ième groupe. Maintenant, calculons \({\bar{R}}_{k}\), le rang moyen donné aux observations dans le k-ième groupe

\[ {\bar{R}}_{k} = \frac{1}{N_{k}}\sum_{i}^{}R_{\text{ik}} \]

et calculons aussi \(\bar{R}\), le rang moyen général

\[ \bar{R} = \frac{1}{N_{k}}\sum_{i}^{}{\sum_{k}^{}R_{\text{ik}}} \]

Maintenant que nous avons fait cela, nous pouvons calculer les écarts quadratiques par rapport au rang moyen général \(\bar{R}\). Lorsque nous le faisons pour les scores individuels, c’est-à-dire si nous calculons \(\left( R_{\text{ik}} - \bar{R} \right)^{2}\) , nous obtenons une mesure « non paramétrique » de l’écart entre la ik-ième observation et le rang moyen général. Lorsque nous calculons l’écart quadratique de la moyenne du groupe par rapport à la grande moyenne, c’est-à-dire si nous calculons \(\left( {\bar{R}}_{k} - \bar{R} \right)^{2}\), nous obtenons une mesure non paramétrique de l’écart entre la moyenne du groupe et la grande moyenne du rang. En gardant cela à l’esprit, nous suivrons la même logique qu’avec ANOVA et définirons nos sommes de carrés de mesures ordonnées, un peu comme nous l’avons fait avec ANOVA plus tôt. Tout d’abord, nous avons notre « total des sommes des carrés ordonnés ».

\[ \text{RSS}_{\text{tot}} = \sum_{k}^{}{\sum_{i}^{}\left( R_{\text{ik}} - \bar{R} \right)^{2}} \]

et on peut définir ainsi les « sommes de carrés ordonnés entre groupes » comme suit

\[\begin{aligned} \text{RSS}_{b} &= \sum_{k}^{}{\sum_{i}^{}\left( \bar{R}_{\text{k}} - \bar{R} \right)^{2}}\\ &= \sum_{k}^{}{N_{k}\left( \bar{R}_{\text{k}} - \bar{R} \right)^{2}} \end{aligned} \]

Si l’hypothèse nulle est vraie et qu’il n’y a aucune différence réelle entre les groupes, on s’attendrait à ce que les sommes RSS_b entre les groupes soient très petites, beaucoup plus petites que le total des sommes RSS_tot. Qualitativement, c’est à peu près la même chose que ce que nous avons trouvé lorsque nous avons construit la statistique F de l’ANOVA, mais pour des raisons techniques, la statistique du test Kruskal-Wallis, habituellement appelée K, est construite d’une manière légèrement différente,

\[ K = (N - 1) \times \frac{\text{RSS}_{b}}{\text{RSS}_{\text{tot}}} \]

et si l’hypothèse nulle est vraie, alors la distribution d’échantillonnage de K est approximativement celle de Khi carré avec G-1 degrés de liberté (où G est le nombre de groupes). Plus la valeur de K est élevée, moins les données sont cohérentes avec l’hypothèse nulle, c’est donc un test unilatéral. Nous rejetons H₀ lorsque K est suffisamment grand.

13.7.2 Détails supplémentaires

La description dans la section précédente illustre la logique derrière le test Kruskal-Wallis. Sur le plan conceptuel, c’est la bonne façon de penser au fonctionnement du test. Cependant, d’un point de vue purement mathématique, c’est inutilement compliqué. Je ne vais pas vous montrer la démonstration, mais vous pouvez utiliser un peu de tambouille algébrique¹¹⁹ pour montrer que l’équation pour K peut être réécrite comme suit

\[ K = \frac{12}{N(N - 1)}\sum_{k}^{}{N_{k}{\bar{R}}_{k}^{2} - 3(N + 1)} \]

C’est cette dernière équation que vous voyez parfois donnée pour K. C’est beaucoup plus facile à calculer que la version que j’ai décrite dans la section précédente, seulement c’est totalement dénué de sens pour les humains. Il est probablement préférable de penser à K comme je l’ai décrit plus tôt, comme un analogue de l’ANOVA basé sur les rangs. Mais gardez à l’esprit que la statistique du test qui est calculée finit par avoir un aspect assez différent de celui que nous avons utilisé pour notre ANOVA originale.

Mais ce n’est pas tout ! Mon Dieu, pourquoi y a-t-il toujours quelque chose en plus ? L’histoire que j’ai racontée jusqu’à présent n’est vraie que lorsqu’il n’y a aucun lien entre les données brutes. C’est-à-dire, s’il n’y a pas deux observations qui ont exactement la même valeur. S’il y a des liens, nous devons introduire un facteur de correction dans ces calculs. À ce stade, je suppose que même le lecteur le plus diligent a cessé de s’en soucier (ou du moins s’est formé l’opinion que le facteur de correction d’égalité est quelque chose qui ne nécessite pas leur attention immédiate). Je vais donc vous dire très rapidement comment il est calculé, et omettre les détails fastidieux des raisons pour lesquelles s’est ainsi. Supposons que nous construisons un tableau de fréquence pour les données brutes, et f_j est le nombre d’observations qui ont la j-ème valeur unique. Cela peut sembler un peu abstrait, alors voici un exemple concret tiré du tableau de fréquence de mood.gain de l’ensemble de données clinicaltrials.csv :

En regardant ce tableau, notez que la troisième entrée du tableau de fréquence a une valeur de 2, ce qui correspond à un mood.gain de 0,3, ce tableau nous indique que l’humeur de deux personnes a augmenté de 0,3. Plus précisément, dans la notation mathématique que j’ai présentée ci-dessus, cela nous dit que f₃=2. Bien, maintenant que nous le savons, le facteur de correction des liens (TCF) est :

\[ TCF = 1 - \frac{\sum_{j}^{}{f_{j}^{3} - f_{j}}}{N^{3} - N} \]

La valeur corrigée de la statistique de Kruskal-Wallis est obtenue en divisant la valeur de K par cette quantité. C’est cette version à ex-aequo corrigés que Jamovi calcule. Enfin, nous en avons fini avec la théorie du test Kruskal-Wallis. Je suis sûr que vous êtes tous terriblement soulagés que je vous aie guéri de l’anxiété existentielle qui surgit naturellement lorsque vous réalisez que vous ne savez pas comment calculer le facteur de correction d’égalité pour le test Kruskal-Wallis. N’est-ce pas ?

13.7.3 Comment exécuter le test Kruskal-Wallis avec Jamovi

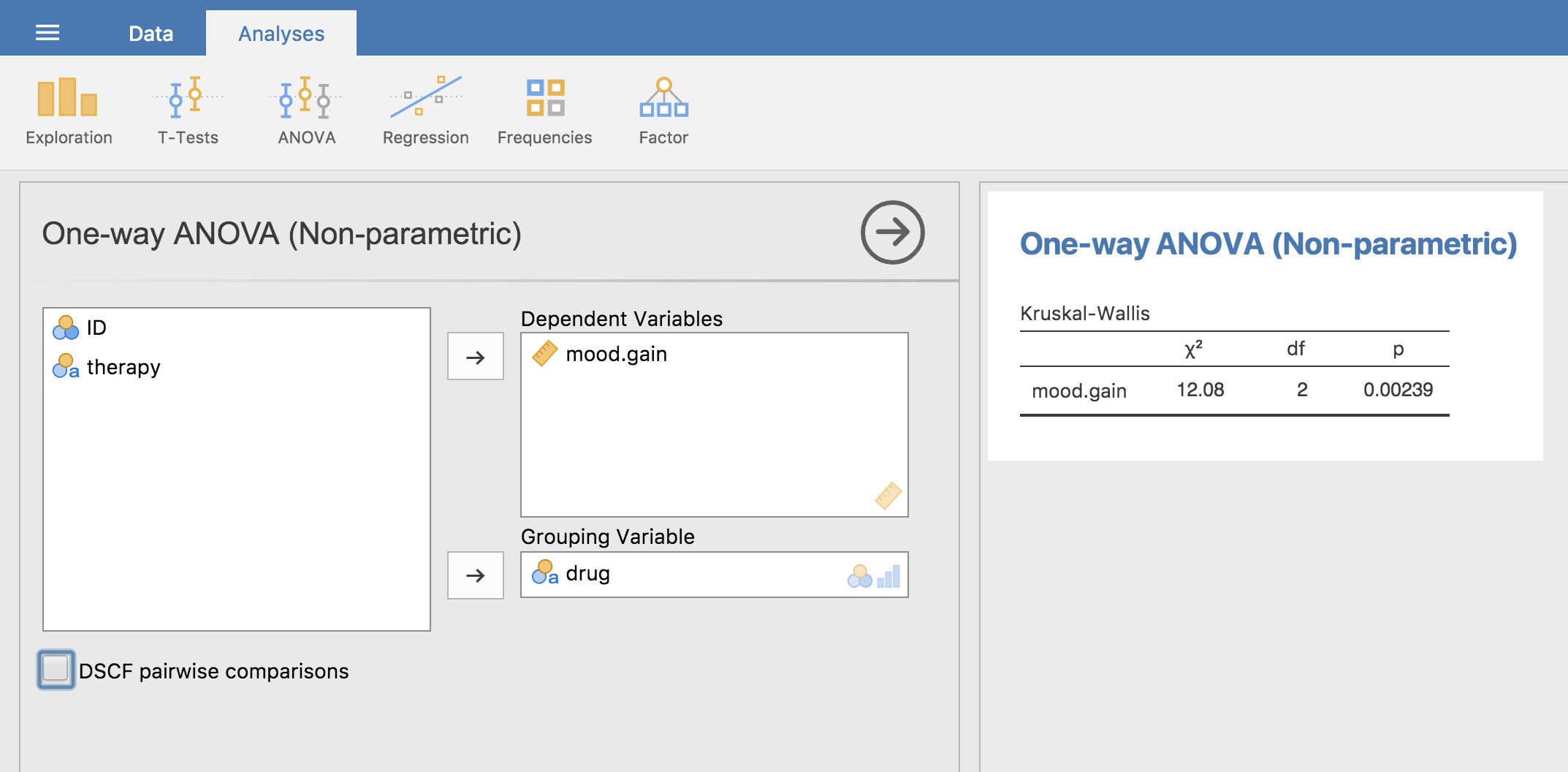
Malgré l’horreur que nous avons vécue en essayant de comprendre ce que fait réellement le test Kruskal-Wallis, il s’avère que l’exécution du test est plutôt indolore, puisque Jamovi a une analyse dans le cadre de l’ensemble d’analyse ANOVA appelé « Non-Parametric » - « One Way ANOVA (Kruskall Wallis) » La plupart du temps, vous aurez les données du type clinicaltrial.csv, où vous avez vos résultats comme la variable mood.gain et des groupes comme la variable drug. Si c’est le cas, vous pouvez procéder à l’analyse avec Jamovi. Voici ce que nous donne est un Kruskal-Wallis \(\chi^{2}=12,076, \text{df}=2, \text{ p-value}= 0,00239\), comme dans la figure 13.8

Figure 13‑8 : Test non paramétrique d’ANOVA à un facteur Kruskall-Wallis avec Jamovi

13.8 ANOVA à un facteur pour mesures appariées

Le test ANOVA à un facteur pour mesures appariée est une méthode statistique de vérification des différences significatives entre trois groupes ou plus où les mêmes participants sont utilisés dans chaque groupe (ou chaque participant est étroitement apparié aux participants d’autres groupes expérimentaux). Pour cette raison, il devrait toujours y avoir un nombre égal de scores (données) dans chaque groupe expérimental. Ce type de conception et d’analyse peut aussi être appelé une « analyse de variance appariée » ou une « analyse de variance intra sujets).

La logique qui sous-tend une analyse de variance pour mesures appariées est très semblable à celle d’une analyse de variance pour groupes indépendants (parfois appelée analyse de variance « inter sujets »). Vous vous souvenez que plus tôt nous avons montré que la variabilité totale de l’ANOVA est divisée en variabilité inter groupes (SS_b) et en variabilité intra groupes (SS_w), et qu’après chacun est divisé par les degrés de liberté respectifs pour donner MS_b et MS_w (voir tableau 13.1) le rapport F est calculé de la manière suivante :

\[ F = \frac{\text{MS}_{b}}{\text{MS}_{w}} \]

Dans une analyse de variance pour mesures appariées, le rapport F est calculé de la même manière, mais alors que dans une analyse de variance pour groupes indépendants, la variabilité intragroupe (SS_w) sert de dénominateur à la MS_w, dans une analyse de variance pour mesures appariées, la SSw est répartie en deux parties. Comme nous utilisons les mêmes sujets dans chaque groupe, nous pouvons supprimer la variabilité due aux différences individuelles entre les sujets, appelées SS_subjects, de la variabilité intra groupe. Nous n’entrerons pas trop dans les détails techniques sur la façon dont cela se fait, mais essentiellement chaque sujet devient un niveau d’un facteur appelé sujets. La variabilité de ce facteur intra-sujets est ensuite calculée de la même manière que tout facteur inter-sujets. Ensuite, nous pouvons soustraire SS_subjects de SS_w pour obtenir un terme SS_error plus petit :

• ANOVA pour groupes indépendants : SS_error = SS_w
• ANOVA pour mesures appariées : SS_error = SS_w - SS_subjects

Ce changement du terme SSerror conduit souvent à un test statistique plus puissant, mais cela dépend du fait que la réduction du SS_error compense largement la réduction des degrés de liberté du valeur d’erreur (les degrés de liberté passant de (n - k)¹²⁰ à (n - 1)(k - 1) (en se rappelant que le plan pour l’ANOVA sur des groupes indépendants contient plus de sujets).

13.8.1 ANOVA pour mesures appariées avec Jamovi

D’abord, il nous faut des données. Geschwind (1972) a suggéré que la nature exacte du déficit du langage d’un patient à la suite d’un AVC peut être utilisée pour diagnostiquer la région spécifique du cerveau qui a été endommagée. Un chercheur s’intéresse à l’identification des difficultés de communication spécifiques éprouvées par six patients souffrant de l’aphasie de Broca (un déficit du langage couramment ressenti à la suite d’un AVC).

Tableau 13‑2 : Nombre de tentatives réussies pour trois tâches expérimentales

Participant	Discours	Conceptuel	Syntaxe
1	8	7	6
2	7	8	6
3	9	5	3
4	5	4	5
5	6	6	2
6	8	7	4

Les patients devaient effectuer trois tâches de reconnaissance de mots. Lors de la première tâche (production de la parole), les patients devaient répéter des mots simples lus à haute voix par le chercheur. Pour la deuxième tâche (conceptuelle), destinée à tester la compréhension des mots, les patients devaient faire correspondre une série d’images avec leur nom correct. Pour la troisième tâche (syntaxique), conçue pour tester la connaissance de l’ordre correct des mots, on a demandé aux patients de réorganiser les phrases syntaxiquement incorrectes. Chaque patient a accompli les trois tâches. L’ordre dans lequel les patients ont tenté les tâches était contrebalancé entre les participants. Chaque tâche consistait en une série de 10 essais. Le nombre d’essai effectués avec succès par chaque patient est indiqué au Tableau 13‑2. Entrez ces données dans Jamovi pour l’analyse (ou prenez un raccourci et chargez le fichier broca.csv).

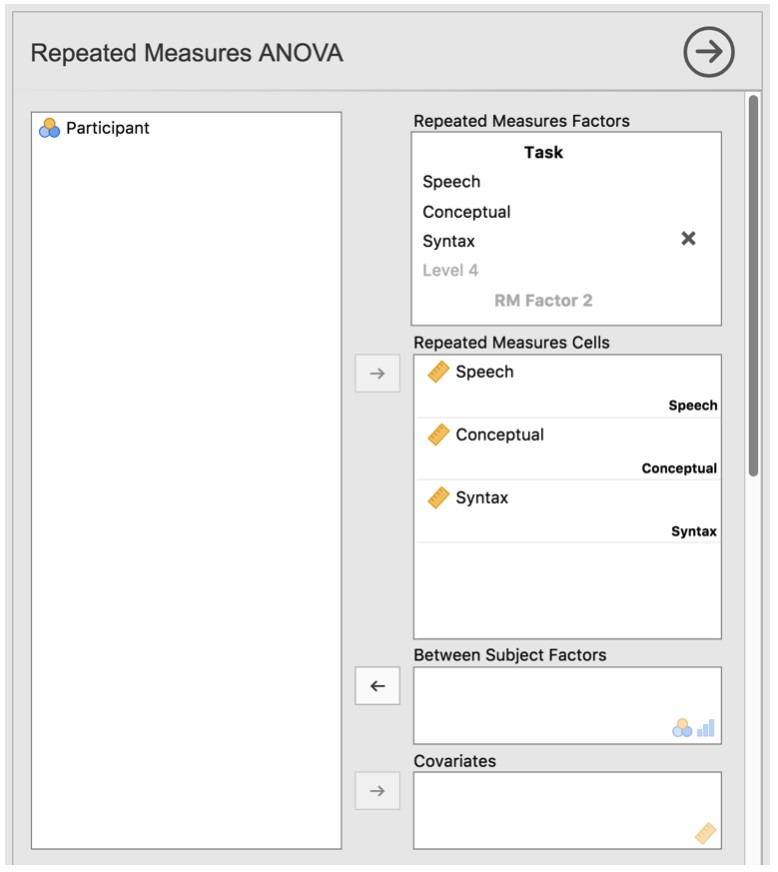
Pour effectuer une ANOVA à un facteur dans Jamovi, ouvrez la boîte de dialogue ANOVA, comme dans la Figure 13‑9, via ANOVA - Repeated Measures ANOVA. Puis :

• Entrez un nom de facteur de mesures appariées. Il s’agit d’une étiquette que vous choisissez pour décrire les conditions répétées pour tous les participants. Par exemple, pour décrire les tâches vocales, conceptuelles et syntaxiques effectuées par tous les participants, une étiquette appropriée serait « Tâche ». Notez que ce nouveau nom de facteur représente la variable indépendante dans l’analyse.

• Ajoutez un troisième niveau dans la zone de texte « Repeated Measures Factors », car il y a trois niveaux représentant les trois tâches : parole, concept et syntaxe. Modifiez les désignations des niveaux en conséquence.

• Ensuite, déplacez chacune des variables de niveau dans la zone de texte « Repeated Measures Cells ».

• Enfin, sous l’option « Assumption Checks », cochez la case « Sphericity checks ».

Figure 13‑9 : Boîte de dialogue ANOVA pour mesures appariées avec Jamovi

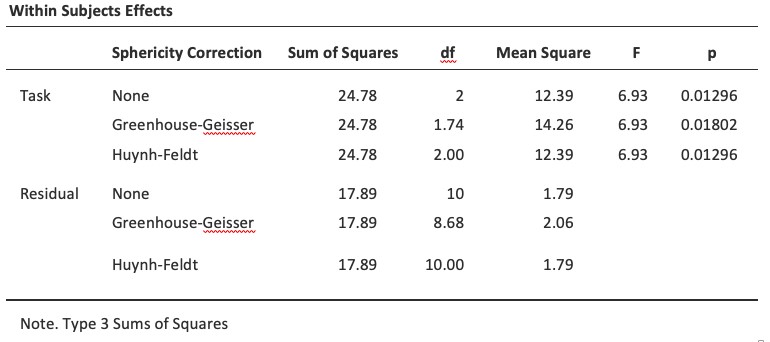
La sortie Jamovi d’une ANOVA à un facteur pour mesures appariées est conformes aux Figure 13‑1 à Figure 13‑13. Le premier résultat que nous devrions examiner est le Test de Mauchly de la sphéricité, qui teste l’hypothèse selon laquelle les variances des différences entre les conditions sont égales (ce qui signifie que l’écart entre les scores des différences entre les conditions de l’étude est approximativement le même). Dans la Figure 13‑10, le niveau de signification du test de Mauchly est p = .720. Si le test de Mauchly n’est pas significatif (c.-à-d. >.05, comme c’est le cas dans la présente analyse), il est raisonnable de conclure que les variances des différences ne sont pas significativement différentes (c.-à-d. qu’elles sont à peu près égales ou que l’on peut supposer la sphéricité).

Figure 13‑10 : résultats de l’ANOVA à un facteur pour mesures appariées : Test de sphéricité de Mauchly

Si, par contre, le test de Mauchly est significatif (p.< .05), nous concluons qu’il y a des différences significatives entre la variance des différences et que l’exigence de sphéricité n’a pas été satisfaite. Dans ce cas, nous devons appliquer une correction à la valeur F obtenue dans l’analyse ANOVA à un facteur.

Si la valeur Greenhouse-Geisser dans le tableau « Tests de sphéricité » est > .75, vous devrez utiliser la correction de Huynh-Feldt. Si la valeur Greenhouse-Geisser est < .75, vous devrez utiliser la correction Greenhouse-Geisser. Ces deux valeurs F corrigées peuvent être spécifiées dans les cases à cocher « Sphericity Corrections » sous les options « Assumption Checks », les valeurs F corrigées sont ensuite affichées dans le tableau des résultats, comme dans la Figure 13‑11.

Figure 13‑11 : Mesure répétée unidirectionnelle de la sortie ANOVA : Tests des effets à l’intérieur des sujets

Dans notre analyse, nous avons vu que la significativité du Test de Mauchly de la sphéricité était p=.720 (c.-à-d. p>.05). Cela signifie donc que nous pouvons supposer que l’exigence de sphéricité a été satisfaite et qu’aucune correction de la valeur F n’est nécessaire. Par conséquent, nous pouvons cocher l’option de correction de sphéricité « None » pour la mesure répétée « Tâche » : F= 6,93, df=2, p= .013, et nous pouvons conclure que le nombre de tests effectués avec succès pour chaque tâche linguistique variait considérablement selon que la tâche était basée sur la parole, la compréhension ou la syntaxe (F(2,10)=6.93,p=.013).

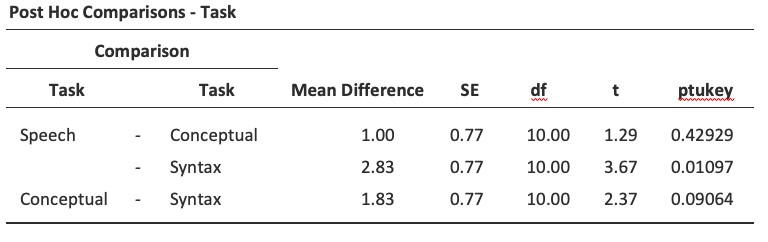
Des tests post-hoc peuvent également être spécifiés dans Jamovi pour les mesures appariées ANOVA de la même manière que pour l’ANOVA sur des groupes indépendants. Les résultats sont présentés à la Figure 13‑12. Ceux-ci indiquent qu’il existe une différence significative entre la parole et la syntaxe, mais pas entre les autres niveaux.

Figure 13‑12 : Tests post-hoc pour une ANOVA pour des mesures appariées avec Jamovi

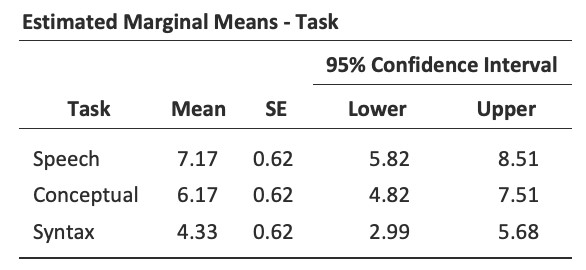
Les statistiques descriptives (moyennes marginales) peuvent être examinées pour aider à interpréter les résultats, produits dans la sortie Jamovi comme dans la Figure 13‑13. La comparaison du nombre moyen d’essais menés avec succès par les participants montre que les Aphasiques de Broca ont d’assez bons résultats dans les domaines suivants la production de la parole (moyenne= 7,17) et la compréhension du langage (moyenne= 6,17). Cependant, leur performance était considérablement plus mauvaise sur la tâche syntaxique (moyenne = 4,33), avec une différence significative aux tests post-hoc entre la parole et la performance de la tâche syntaxique.

Figure 13‑13 : Statistiques descriptives pour l’ANOVA à un facteur pour mesure appariées :

13.9 Le test non paramétrique de Friedman

Le test de Friedman est une version non paramétrique d’une analyse de variance pour mesures appariées et peut remplacer le test de Kruskall-Wallis lorsqu’il s’agit de déterminer les différences entre trois groupes ou plus où les mêmes participants font partie de chaque groupe, ou lorsque chaque participant est étroitement apparié avec des participants d’autres conditions. Si la variable dépendante est ordinale ou si l’hypothèse de normalité n’est pas respectée, on peut utiliser le test de Friedman.

Figure 13‑14 : La boîte de dialogue « Repeated Measures ANOVA (Non-parametric) » dans Jamovi

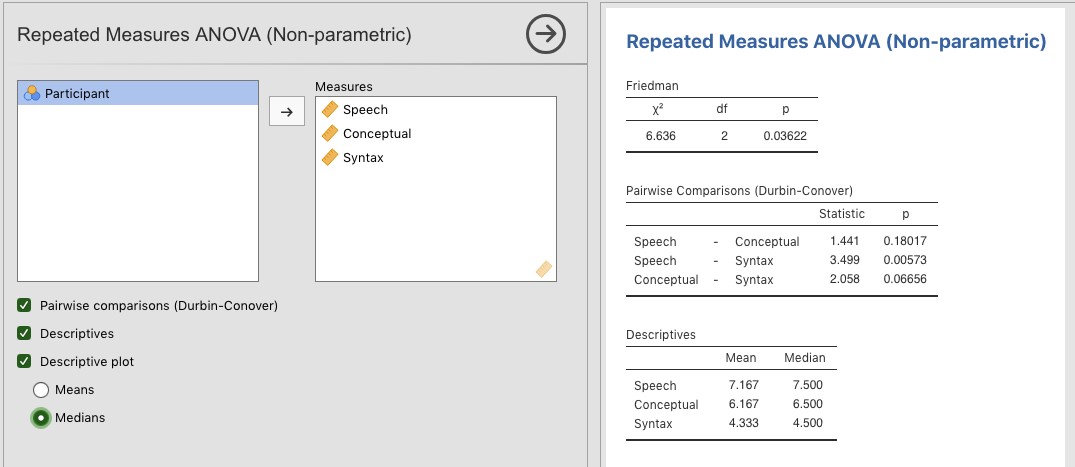
Comme pour le test Kruskall-Wallis, les mathématiques sous-jacentes sont compliquées et ne seront pas présentées ici. Pour les besoins de ce livre, il suffit de noter que Jamovi calcule la version corrigée du test de Friedman dont la Figure 13‑14 est un exemple utilisant les données sur l’aphasie de Broca que nous avons déjà examinées en utilisant une analyse de variance à un facteur paramétrique.

Il est assez simple de faire un test de Friedman avec Jamovi. Sélectionnez simplement « Analyses - ANOVA - Repeated Measures ANOVA (Non-parametric) », comme dans la Figure 13‑14. Ensuite, sélectionnez et transférez les variables de mesures appariées que vous souhaitez comparer (Parole, Conceptuel, Syntaxe) dans la zone de texte « Measures : ». Pour produire des statistiques descriptives (moyennes et médianes) pour les trois variables de mesures appariés, cliquez sur le bouton « Descriptives ».

Les résultats de Jamovi montrent des statistiques descriptives, la valeur du chi carré, les degrés de liberté et la valeur p (Figure 13‑14). Puisque la valeur p est inférieure au niveau conventionnellement utilisé pour déterminer la signification (p< .05), nous pouvons conclure que les Aphasiques de Broca donnent de bons résultats dans les tâches de production de la parole (médiane=7,5) et de compréhension du langage (médiane=6,5). Cependant, leur performance était considérablement plus mauvaise sur la tâche syntaxique (médiane=4.5), avec une différence significative aux tests post-hoc entre la parole et la performance de la tâche syntaxique.

13.10 Sur la relation entre ANOVA et le test t de Student

Il y a une dernière chose que je tiens à souligner avant de terminer. C’est quelque chose que beaucoup de gens trouvent un peu surprenant, mais cela vaut la peine d’en savoir plus. Une ANOVA sur deux groupes est identique au t de Student. Ils ne sont pas seulement semblables, en fait ils sont équivalents en tous points de vue. Je n’essaierai pas de prouver que c’est toujours vrai, mais je vais vous fournir une seule démonstration concrète. Supposons qu’au lieu d’exécuter une analyse de variance sur notre modèle mood.gain ~ drug, nous utilisons plutôt la therapy comme prédicteur. Si nous exécutons cette ANOVA, nous obtenons une statistique F de F(1,16)=1,71, et une valeur p= 0,21. Comme nous n’avons que deux groupes, je n’ai pas besoin de recourir à une ANOVA, j’aurais pu simplement décider de faire un t de Student. Voyons ce qui se passe quand je fais ça : J’obtiens une statistique t de t(16)=-1,3068 et une valeur p=0.21. Curieusement, les valeurs p sont identiques. Une fois de plus, on obtient une valeur de p = .21. Mais qu’en est-il de la statistique du test ? Après avoir effectué un test t au lieu d’une ANOVA, nous obtenons une réponse quelque peu différente, à savoir t(16)= -1,3068. Cependant, il existe une relation assez simple avec F. Si nous élevons au carré la statistique t, nous obtenons la statistique F précédente : -1,3068² = 1,7077

13.11 Résumé

Il y a beaucoup de choses dans ce chapitre, mais il en manque encore beaucoup. De toute évidence, je n’ai pas encore discuté d’un analogue du test t pour des échantillons appariés pour plus de deux groupes. Il y a une façon de le faire, connue sous le nom de ANOVA pour mesures répétées, qui apparaîtra plus tard. Je n’ai pas non plus discuté de la façon d’exécuter une analyse de variance lorsque vous vous intéressez à plus d’une variable de regroupement, mais cela sera discuté en détail au chapitre 14. Pour ce que nous avons présenté, les sujets clés étaient :

• La logique de base du fonctionnement de l’ANOVA (Section 13.2) et la façon de l’exécuter avec Jamovi (Section 13.3).

• Comment calculer la taille de l’effet d’une analyse de variance (section 13.4)

• Analyse post hoc et corrections pour les tests multiples (section 13.5).

• Les hypothèses sous-jacents à l’ANOVA (section 13.6).

• Comment vérifier l’hypothèse d’homogénéité de la variance (section 13.6.1).

• Comment vérifier l’hypothèse de normalité (Section 13.6.4) et que faire si elle est violée (Section 13.7).

• ANOVA pour mesures appariées (section 13.8) et l’équivalent non paramétrique, le test de Friedman (section 13.9).

Comme pour tous les chapitres de ce livre, il y a un certain nombre de sources différentes sur lesquelles je me suis appuyé, mais le texte qui m’a le plus influencé est Sahai et Ageel (2000). Ce n’est pas un bon livre pour les débutants, mais c’est un excellent livre pour les lecteurs plus avancés qui sont intéressés à comprendre les fondements mathématiques de l’ANOVA.

References

Box, G. E. P. 1953. “Non-Normality and Tests on Variances.” Biometrika 40 (3/4): 318–35. https://doi.org/10.2307/2333350.

Brown, Morton B., and Alan B. Forsythe. 1974. “Robust Tests for the Equality of Variances.” Journal of the American Statistical Association 69 (346): 364–67. https://doi.org/10.2307/2285659.

Dunn, Olive Jean. 1961. “Multiple Comparisons Among Means.” Journal of the American Statistical Association 56 (293): 52–64. https://doi.org/10.1080/01621459.1961.10482090.

Geschwind, Norman. 1972. “Language and the Brain.” Scientific American 226 (4): 76–83.

Holm, Sture. 1979. “A Simple Sequentially Rejective Multiple Test Procedure.” Scandinavian Journal of Statistics 6 (2): 65–70.

Hsu, Jason. 1996. Multiple Comparisons: Theory and Methods. London: Chapman and Hall/CRC.

Kruskal, William H., and W. Allen Wallis. 1952. “Use of Ranks in One-Criterion Variance Analysis.” Journal of the American Statistical Association 47 (260): 583–621. https://doi.org/10.2307/2280779.

Levene, H. 1960. “Robust Tests for Equality of Variances.” In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling, edited by I. Oklin, Sudhish G. Ghurye, w; Hoeffding, W. G. Madow, and Henry B. Mann, 278–92. Palo Alto, CA: Stanford University Press.

Sahai, Hardeo, and Mohammed I. Ageel. 2000. The Analysis of Variance: Fixed, Random and Mixed Models. Birkhäuser Basel. https://doi.org/10.1007/978-1-4612-1344-4.

Shaffer, J P. 1995. “Multiple Hypothesis Testing.” Annual Review of Psychology 46 (1): 561–84. https://doi.org/10.1146/annurev.ps.46.020195.003021.

Welch, B. 1951. “On the Comparison of Several Mean Values: An Alternative Approach.” Biometrika 38 (3/4): 330–36. https://doi.org/10.2307/2332579.

---

109. Lorsque tous les groupes ont le même nombre d’observations, le plan expérimental est dit « équilibré ». L’équilibre n’est pas si important pour l’ANOVA à un facteur, qui est le sujet de ce chapitre. Cela devient plus important lorsque vous commencez à faire des analyses de variance plus complexes.↩︎

110. SS_w correspond aussi dans l’ANOVA pour groupes indépendants à la variance de l’erreur ou SS_error↩︎

111. Si vous lisez le chapitre 14 et regardez comment « l’effet de traitement » au niveau k d’un facteur est défini en termes de valeurs \(\alpha_{k}\) (voir section 14.1.2), il s’avère que Q fait référence à une moyenne pondérée des effets du traitement au carré, \(Q = \left( \sum_{k = 1}^{G}{N_{k}\alpha_{k}^{2}} \right)/\left( G - 1 \right)\)↩︎

112. Ou, si nous voulons être pointilleux sur la précision, \(1 + \frac{2}{\text{df}_{2} - 2}\)↩︎

113. Ou, pour être plus précis, un jeu comme si « nous sommes en 1899 et nous n’avons pas d’amis et rien de mieux à faire avec notre temps que de faire des calculs qui n’auraient pas eu de sens en 1899 car ANOVA n’existait pas avant les années 1920 ».↩︎

114. Dans le fichier Excel clinicaltrial_anova.xls, la valeur pour SS_b est très légèrement différente, 3,45, de celle indiquée dans le texte ci-dessus (erreurs d’arrondi !).↩︎

115. Les résultats de Jamovi sont plus précis que ceux du texte ci-dessus, en raison d’erreurs d’arrondi.↩︎

116. http://daniellakens.blogspot.com.au/2015/06/why-you-should-utilisation-omega-squared.html↩︎

117. Si vous avez une base théorique pour vouloir examiner certaines comparaisons, mais pas d’autres, c’est une autre histoire. Dans ces circonstances, vous n’effectuez pas du tout des analyses « post hoc », vous faites des « comparaisons planifiées ». Je parlerai de cette situation plus loin dans le livre (Section 14.9), mais pour l’instant, je veux que les choses restent simples.↩︎

118. Il convient de noter au passage que toutes les méthodes d’ajustement n’essaient pas de le faire. Ce que j’ai décrit ici est une approche pour contrôler le « taux d’erreur de type I pour les familles ». Cependant, il existe d’autres tests post hoc qui visent à contrôler le « taux de fausses découvertes », ce qui est un peu différent.↩︎

119. Un terme technique↩︎

120. (n - k) : (nombre de sujets - nombre de groupes)↩︎