Chapitre 12 Corrélation et régression linéaire

Le but de ce chapitre est d’introduire la corrélation et la régression linéaire. Ce sont les outils standard sur lesquels les statisticiens s’appuient pour analyser la relation entre les prédicteurs continus et les résultats continus.

12.1 Corrélations

Dans cette section, nous verrons comment décrire les relations entre les variables des données. Pour ce faire, nous voulons surtout parler de la corrélation entre les variables. Mais d’abord, il nous faut des données.

12.1.1 Les données

Tableau 12‑1 Statistiques descriptives pour les données sur la parentalité (parenthood data)

variable	min	max	mean	median	Std. dev	IQR
Grinchiosité de Dan	41	91	63,71	62	10,05	14
Les heures de sommeil de Dan	4,84	9,00	6,97	7,03	1,02	1,45
Les heures de sommeil du fils de Dan	3,25	12,07	8,05	7,95	2,07	3,21

Parlons d’un sujet qui tient à cœur à tous les parents : le sommeil. L’ensemble de données que nous utiliserons est fictif, mais basé sur des événements réels. Supposons que je sois curieux de savoir dans quelle mesure les habitudes de sommeil de mon fils influent sur mon humeur. Disons que je peux évaluer mon caractère grincheux très précisément, sur une échelle allant de 0 (pas du tout grincheux) à 100 (grincheux comme un vieil homme ou une vieille femme très, très grincheux). Et supposons aussi que je mesure ma mauvaise humeur, mes habitudes de sommeil et celles de mon fils depuis un certain temps déjà. Disons, pour 100 jours. Et, étant un intello, j’ai sauvegardé les données dans un fichier appelé parenthood.csv. Si nous chargeons les données, nous pouvons voir que le fichier contient quatre variables : dan.sleep, baby.sleep, dan.grump et day. Notez que lorsque vous chargez pour la première fois cet ensemble de données, Jamovi n’a peut-être pas deviné correctement le type de données pour chaque variable, auquel cas vous devrez le corriger : dan.sleep, baby.sleep, dan.grump et day peuvent être spécifiés comme variables continues, et ID est une variable nominale (entier).⁹²

Ensuite, j’examinerai quelques statistiques descriptives de base et, pour donner une représentation graphique de ce à quoi ressemble chacune des trois variables d’intérêt, la Figure 12‑1 présente les histogrammes. Une chose à noter : ce n’est pas parce que Jamovi peut calculer des douzaines de statistiques différentes que vous devez les rapporter toutes. Si je devais rédiger ce rapport, je choisirais probablement les statistiques qui m’intéressent le plus (et qui intéressent mon lectorat), puis je les regrouperais dans un tableau simple et agréable comme celui du Tableau 12‑1⁹³. Remarquez que lorsque je l’ai mis dans un tableau, j’ai donné à tous des noms « en langage naturel ». C’est toujours une bonne pratique. Remarquez aussi que je ne dors pas assez. Ce n’est pas une bonne pratique, mais d’autres parents me disent que c’est la norme.

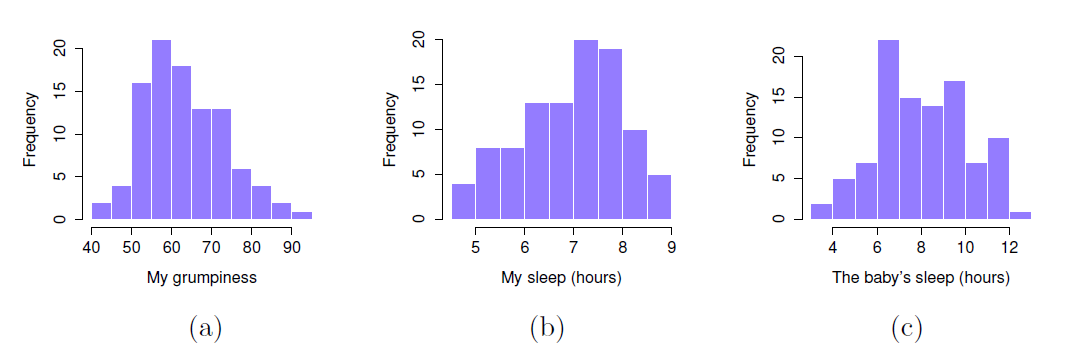
Figure 12‑1 : Histogrammes pour les trois variables d’intérêt de l’ensemble de données sur la parentalité.

12.1.2 La force et l’orientation d’une relation

Nous pouvons dessiner des diagrammes de dispersion pour nous donner une idée générale du degré de corrélation entre deux variables. Idéalement, cependant, nous voudrions peut-être en dire un peu plus à ce sujet. Par exemple, comparons la relation entre dan.sleep et dan.grump (Figure 12‑2, à gauche) avec celle entre baby.sleep et dan.grump (Figure 12‑2, à droite). En regardant ces deux figures côte à côte, il est clair que la relation est qualitativement la même dans les deux cas : plus de sommeil égale moins de grinchiosité ! Cependant, il est aussi assez évident que la relation entre dan.sleep et dan.grump est plus forte que la relation entre baby.sleep et dan.grump. La figure de gauche est « plus nette » que celle de droite. Il me semble que si vous vouliez prédire mon humeur, cela vous aiderait un peu de savoir combien d’heures mon fils a dormi, mais ce serait plus utile de savoir combien d’heures j’ai dormi.

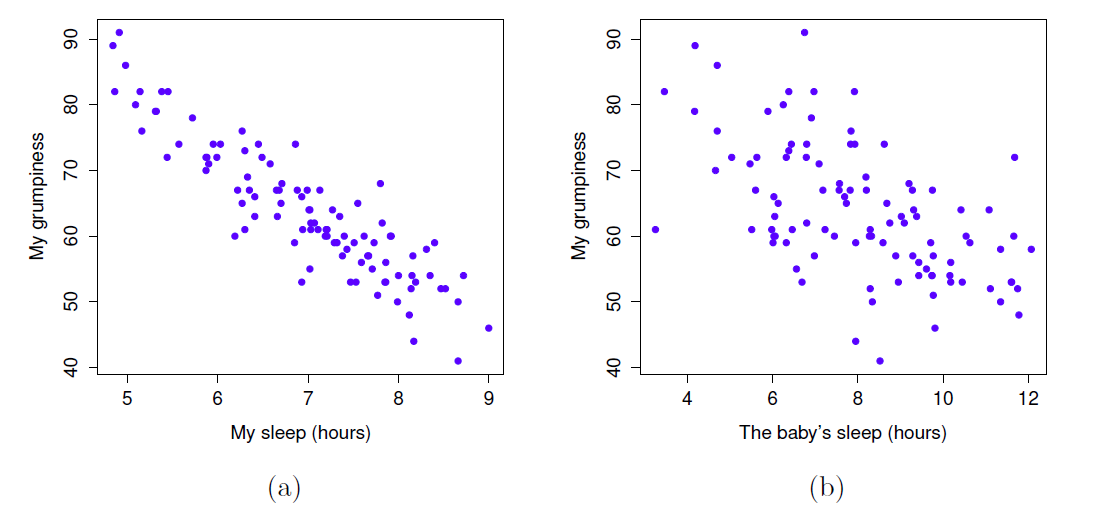
Figure 12‑2 : Diagrammes de dispersion montrant la relation entre dan.sleep et dan.grump (à gauche) et la relation entre baby.sleep et dan.grump (à droite)

En revanche, considérons les deux diagrammes de dispersion illustrés à la Figure 12‑3. Si l’on compare le nuage de points de « baby.sleep et dan.grump » (à gauche) au nuage de points de « baby.sleep et dan.sleep » (à droite), la force globale de la relation est la même, mais la direction est différente. C’est-à-dire, si mon fils dort plus, je dors plus (relation positive, côté droit), mais s’il dort plus, je suis moins grincheux (relation négative, côté gauche).

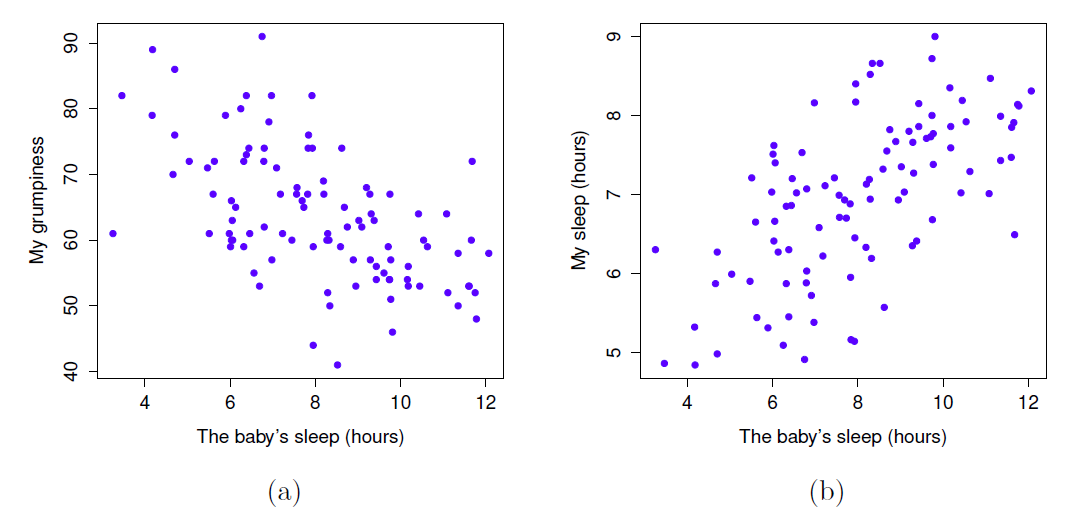
Figure 12‑3 : Diagrammes de dispersion montrant la relation entre baby.sleep et dan.grump (à gauche), par rapport à la relation entre baby.sleep et dan.sleep (à droite).

12.1.3 Le coefficient de corrélation

Nous pouvons rendre ces idées un peu plus explicites en introduisant l’idée d’un coefficient de corrélation (ou, plus précisément, le coefficient de corrélation de Pearson), traditionnellement appelé r. Le coefficient de corrélation entre deux variables X et Y (parfois appelé r_XY), que nous allons définir plus précisément dans la section suivante, est une mesure qui varie entre -1 et 1. Quand r=-1 signifie que nous avons une relation négative parfaite, et quand r=1 signifie que nous avons une relation positive parfaite. Quand r=0, il n’y a pas de relation du tout. Si vous regardez la Figure 12‑4, vous pouvez voir plusieurs graphiques montrant à quoi ressemblent différentes corrélations.

La formule du coefficient de corrélation de Pearson peut être écrite de plusieurs façons. Je pense que la façon la plus simple d’écrire la formule est de la diviser en deux étapes. Tout d’abord, introduisons l’idée d’une covariance. La covariance entre deux variables X et Y est une généralisation de la notion de variance et est un moyen mathématiquement simple de décrire la relation entre deux variables qui n’est pas très instructive pour l’homme.

\[ \text{Cov}\left( X,Y \right) = \ \frac{1}{N}\sum_{i=1}^{N}{\left( X_{i} - \bar{X} \right)\left( Y_{i} - \bar{Y} \right)} \]

Puisque nous multiplions (c’est-à-dire que nous prenons le « produit ») d’une quantité qui dépend de X par une quantité qui dépend de Y et que nous calculons ensuite la moyenne⁹⁴, vous pouvez considérer la formule de la covariance comme un « produit croisé moyen » entre X et Y.

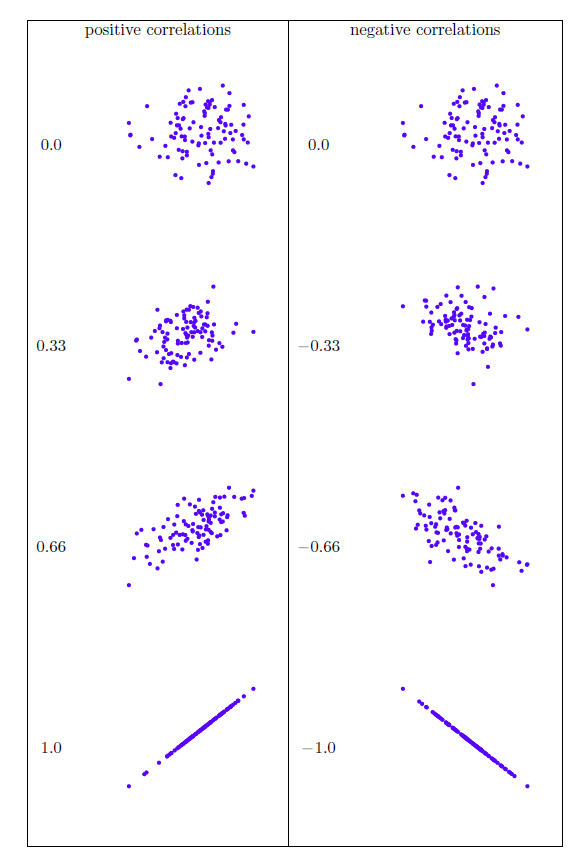
Figure 12‑4 : Illustration de l’effet de la variation de l’intensité et de la direction d’une corrélation. Dans la colonne de gauche, les corrélations sont 0; 0,33; 0,66 et 1 ; dans la colonne de droite, les corrélations sont 0; -0,33; -0,66 et -1.

La covariance a la propriété intéressante que, si X et Y sont entièrement indépendants, alors la covariance est exactement nulle. Si la relation entre eux est positive (au sens de la Figure 12‑4), la covariance est également positive, et si la relation est négative, la covariance est également négative. En d’autres termes, la covariance saisit l’idée qualitative fondamentale de corrélation. Malheureusement, l’amplitude brute de la covariance n’est pas facile à interpréter car elle dépend des unités dans lesquelles X et Y sont exprimés et, pire encore, les unités réelles dans lesquelles la covariance elle-même est exprimée sont vraiment étranges. Par exemple, si X fait référence à la variable dan.sleep (unités : heures) et Y à la variable dan.grump (unités : grinchiosité), alors les unités pour leur covariance sont « heures X grinchiosité ». Je n’ai aucune idée de ce que ça peut vouloir dire.

Le coefficient de corrélation de Pearson r corrige ce problème d’interprétation en normalisant la covariance, à peu près de la même manière que le score z normalise un score brut, en divisant par l’écart type. Cependant, comme nous avons deux variables qui contribuent à la covariance, la standardisation ne fonctionne que si nous divisons par les deux écarts-types⁹⁵. En d’autres termes, la corrélation entre X et Y peut être écrite comme suit :

\[ r_{XY} = \frac{Cov(X,Y)}{{\hat{\sigma}}_{X}{\hat{\sigma}}_{y}} \]

En standardisant la covariance, non seulement nous conservons toutes les belles propriétés de la covariance discutée précédemment, mais les valeurs réelles de r sont sur une échelle significative : r=1 implique une relation positive parfaite et r=-1 implique une relation négative parfaite. Je reviendrai un peu plus en détail sur ce point plus tard, à la section 12.1.5 Mais avant, voyons comment calculer les corrélations dans Jamovi.

12.1.4 Calcul des corrélations dans Jamovi

Le calcul des corrélations dans Jamovi peut se faire en cliquant sur le menu « Regression » - « Correlation Matrix ». Transférez les quatre variables continues dans la boîte de droite pour obtenir le résultat de la Figure 12‑5.

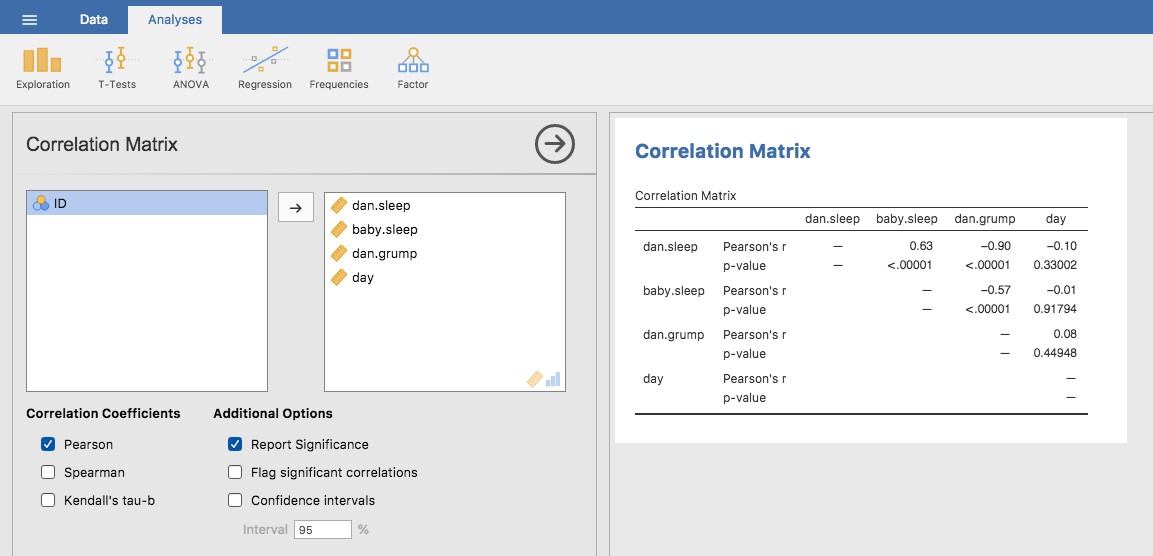
Figure 12‑5 : Une capture d’écran Jamovi montrant les corrélations entre les variables du fichierparenthood.csv

12.1.5 Interpréter une corrélation

Naturellement, dans la vie réelle, on ne voit pas beaucoup de corrélations de 1. Alors comment interpréter une corrélation de, disons, r=0,4 ? La réponse honnête est que cela dépend vraiment de la raison pour laquelle vous voulez utiliser les données et de l’importance des corrélations dans votre domaine. Un de mes amis en ingénierie m’a dit un jour que toute corrélation inférieure à 0,95 est complètement inutile (je pense qu’il exagérait, même pour l’ingénierie). D’un autre côté, il y a des cas réels, même en psychologie, où il faut vraiment s’attendre à des corrélations aussi fortes. Par exemple, l’un des ensembles de données de référence utilisés pour tester les théories sur la façon dont les gens jugent les similarités est si spécifique que toute théorie qui ne peut pas atteindre une corrélation d’au moins 0,9 n’est pas vraiment considéré comme un succès. Cependant, lorsque vous recherchez (disons) des corrélats élémentaires d’intelligence (p. ex. temps d’inspection, temps de réponse), si vous obtenez une corrélation supérieure à 0,3, c’est un bon résultat. Bref, l’interprétation d’une corrélation dépend beaucoup du contexte. Cela dit, le guide approximatif du Tableau 12‑2 est assez typique.

Tableau 12‑2 : Un guide approximatif pour interpréter les corrélations. Notez que je dis un guide approximatif. Il n’y a pas de règles strictes pour ce qui est des relations fortes ou faibles. Cela dépend du contexte.

Corrélation	Force	Direction
-1,0 à -0,9	Très fort	Négatif
-0,9 à -0,7	Fort	Négatif
-0,7 à -0,4	Modéré	Négatif
-0,4 à -0,2	Faible	Négatif
-0,2 à 0	Négligeable	Négatif
0 à 0,2	Négligeable	Positif
0,2 à 0,4	Faible	Positif
0,4 à 0,7	Modéré	Positif
0,7 à 0,9	Fort	Positif
0,9 à 1,0	Très fort	Positif

Cependant, ce qu’on ne soulignera jamais assez, c’est qu’il faut toujours regarder le nuage de points avant de faire toute interprétation des données. Une corrélation peut ne pas signifier ce que vous pensez qu’elle signifie. L’illustration classique est fourni par « le Quatuor d’Anscombe » (Anscombe 1973), une collection de quatre ensembles de données. Chaque ensemble de données comporte deux variables, un X et un Y. Pour les quatre données la valeur moyenne pour X à 9 et la moyenne pour Y à 7,5. Les écarts-types pour toutes les variables X sont presque identiques, tout comme ceux des variables Y. Et dans chaque cas, la corrélation entre X et Y est r=0,816. Vous pouvez le vérifier vous-même, car il se trouve que je l’ai sauvegardé dans un fichier appelé anscombe.csv.

On pourrait penser que ces quatre ensembles de données se ressemblent beaucoup. Ce n’est pas le cas. Si nous dessinons des diagrammes de dispersion de X par rapport à Y pour les quatre variables, comme le montre la Figure 12‑6, nous constatons que ces quatre variables sont très différentes les unes des autres. La leçon ici, que tant de gens semblent oublier dans la vie réelle, est qu’il faut toujours tracer un graphique de vos données brutes (chapitre 5).

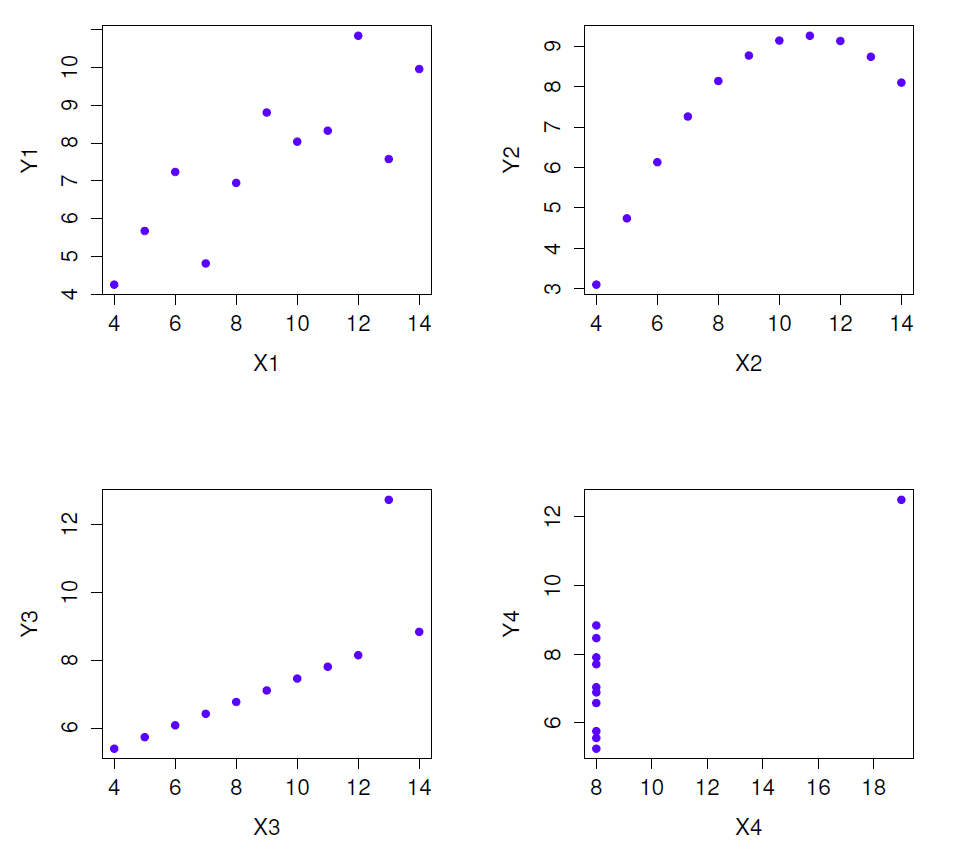
Figure 12‑6 : Le quatuor d’Anscombe. Ces quatre ensembles de données ont une corrélation de Pearson de r = 0,816, mais ils sont qualitativement différents les uns des autres.

12.1.6 Corrélations de rang de Spearman

Le coefficient de corrélation de Pearson est utile pour beaucoup de choses, mais il comporte des lacunes. Une question en particulier ressort : ce qu’il mesure en fait, c’est la force de la relation linéaire entre deux variables. En d’autres termes, ce qu’il vous donne est une mesure de la tendance des données à toutes s’aligner sur une seule ligne parfaitement droite. Souvent, il s’agit d’une assez bonne approximation de ce que nous entendons par « relation », et il est pertinent de calculer la corrélation de Pearson. Mais parfois, ça ne l’est pas.

Une situation très courante où la corrélation de Pearson n’est pas tout à fait ce qu’il faut utiliser survient lorsqu’une augmentation d’une variable X se reflète réellement dans une augmentation d’une autre variable Y, mais que la nature de la relation n’est pas nécessairement linéaire. Un exemple de cela pourrait être la relation entre l’effort et la récompense lorsqu’on étudie pour un examen. Si vous ne faites aucun effort (X) pour apprendre une matière, vous devez vous attendre à obtenir une note de 0 % (Y). Cependant, un peu d’effort entraînera une amélioration massive. Le simple fait d’assister à des cours magistraux vous permet d’apprendre pas mal de choses, et si vous venez en classe et que vous griffonnez quelques notes, votre score pourrait atteindre 35 %, le tout sans beaucoup d’efforts. Cependant, vous n’obtenez pas le même effet à l’autre bout de l’échelle. Comme tout le monde le sait, il faut beaucoup plus d’efforts pour obtenir une note de 90 % que pour obtenir une note de 55 %. Ce que cela signifie, c’est que, si j’ai des données sur l’effort d’étude et les notes, il y a de fortes chances que les corrélations de Pearson soient trompeuses.

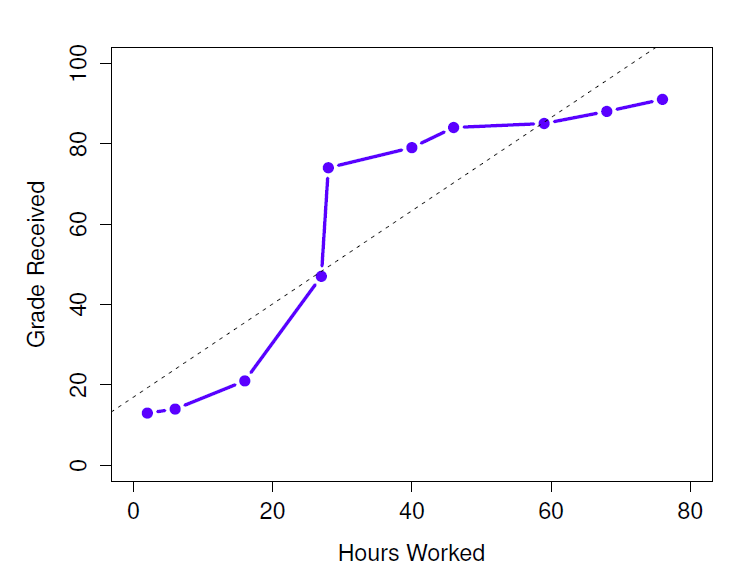
Figure 12‑7 : La relation entre les heures travaillées et la note reçue pour un ensemble de données fictif composé de seulement 10 élèves (chaque point correspond à un élève). La ligne en pointillés au milieu montre la relation linéaire entre les deux variables. Ceci produit une forte corrélation de Pearson de r=0,91. Cependant, ce qu’il est intéressant de noter ici, c’est qu’il y a en fait… une relation monotone parfaite entre les deux variables. Dans cet exemple fictif, l’augmentation des heures travaillées accroît toujours la note reçue, comme l’illustre le trait plein. Cela se reflète dans une corrélation Spearman de 1. Avec un si petit ensemble de données, cependant, c’est une question ouverte que de savoir quelle version décrit le mieux la relation réelle impliquée.

A titre d’exemple, examinons les données illustrées à la Figure 12‑7, qui montrent la relation entre les heures travaillées et la note reçue pour 10 élèves qui suivent un cours. Ce qui est curieux dans cet ensemble de données (hautement fictif), c’est que le fait d’augmenter votre effort augmente toujours votre note. Il peut être de beaucoup ou d’un peu, mais un effort accru ne diminuera jamais votre note. Si nous utilisons une corrélation standard de Pearson, elle montre une forte relation entre les heures travaillées et la note reçue, avec un coefficient de corrélation de 0,91. Toutefois, cela ne tient pas compte du fait que l’augmentation du nombre d’heures travaillées fait toujours augmenter la note. Il y a ici un sens dans lequel nous voulons pouvoir dire que la corrélation est parfaite mais pour une notion quelque peu différente de ce qu’est une « relation ». Ce que nous recherchons, c’est quelque chose qui saisit le fait qu’il y a une relation ordinale parfaite ici. Autrement dit, si l’élève 1 travaille plus d’heures que l’élève 2, nous pouvons garantir que l’élève 1 obtiendra la meilleure note. Ce n’est pas du tout ce que signifie une corrélation de r=0,91.

Comment devrions-nous aborder cette question ? En fait, c’est très facile. Si nous recherchons des relations ordinales, tout ce que nous avons à faire est de traiter les données comme s’il s’agissait d’une échelle ordinale ! Ainsi, au lieu de mesurer l’effort en termes « d’heures travaillées », classons les 10 étudiants par ordre d’heures travaillées. C’est-à-dire que l’élève 1 a fait le moins de travail de n’importe qui (2 heures), de sorte qu’il obtient le rang le plus bas (rang = 1). L’étudiant 4 était le deuxième plus paresseux, n’ayant travaillé que 6 heures sur l’ensemble du semestre, de sorte qu’il obtient le deuxième rang le plus bas (rang = 2). Notez que j’utilise « rang = 1 » pour signifier « rang faible ». Parfois, dans le langage courant, on parle de « rang = 1 » pour signifier « rang le plus élevé » plutôt que « rang le plus bas ». Soyez donc prudent, vous pouvez classer « de la plus petite valeur à la plus grande valeur » (c.-à-d. petit égal 1) ou « de la plus grande valeur à la plus petite valeur » (c.-à-d., grand égal 1). Dans ce cas, je classe du plus petit au plus grand, mais comme il est vraiment facile d’oublier la façon dont vous organisez les choses, il faut faire un effort d’attention !

Jetons donc un coup d’œil à nos élèves quand nous les classons du pire au meilleur en termes d’effort et de récompense :

	rang (heures travaillées)	rang (note reçue)
élève 1	1	1
élève 2	10	10
élève 3	6	6
élève 4	2	2
élève 5	3	3
élève 6	5	5
élève 7	4	4
élève 8	8	8
élève 9	7	7
étudiant 10	9	9

Ils sont pareils. L’étudiant qui a fait le plus d’efforts a obtenu la meilleure note, l’étudiant qui a fait le moins d’efforts a obtenu la pire note, etc. Comme le montre le tableau ci-dessus, ces deux classements sont identiques, donc si nous les calculons une corrélation maintenant, nous obtenons une relation parfaite, avec une corrélation de 1.

Ce que nous venons de réinventer, c’est la corrélation par rang de Spearman, habituellement désignée \(\rho\) pour la distinguer de la corrélation de Pearson r. Nous pouvons calculer la corrélation de Spearman \(\rho\) en utilisant Jamovi simplement en cochant la case « Spearman » dans « Correlation Matrix ».

12.2 Diagrammes de dispersion

Les nuages de points sont un outil simple mais efficace pour visualiser la relation entre deux variables, comme nous l’avons vu avec les chiffres de la section sur la corrélation (Section 12.1). C’est cette dernière application que nous avons généralement en tête lorsque nous utilisons le terme « nuage de points ». Dans ce type de graphique, chaque observation correspond à un point. L’emplacement horizontal du point trace la valeur de l’observation sur une variable et l’emplacement vertical affiche sa valeur sur l’autre variable. Dans de nombreuses situations, vous n’avez pas vraiment d’opinion claire sur la nature de la relation causale (p. ex., est-ce que A cause B, ou est-ce que B cause A, ou est-ce qu’une autre variable C contrôle à la fois A et B). Si c’est le cas, peu importe quelle variable vous tracez sur l’axe des x et celle que vous tracez sur l’axe des y. Cependant, dans de nombreuses situations, vous avez une idée assez précise de la variable que vous pensez être la plus susceptible d’être causale, ou du moins vous avez quelques soupçons pour cela. Si c’est le cas, il est conventionnel de tracer la variable cause sur l’axe des x, et la variable effet sur l’axe des y. En gardant cela à l’esprit, voyons comment dessiner des nuages de points dans Jamovi, en utilisant le même ensemble de données sur la parentalité (i.e. parenthood.csv) que celui que j’ai utilisé pour introduire les corrélations.

Supposons que mon but est de dessiner un nuage de points montrant la relation entre la quantité de sommeil que j’obtiens (dan.sleep) et à quel point je suis grincheux le jour suivant (dan.grump). Il y a deux façons différentes d’utiliser Jamovi pour obtenir le graphique que nous recherchons. La première façon est d’utiliser l’option « Tracé » sous le bouton « Régression » - « Matrice de corrélation », ce qui nous donne la sortie indiquée dans la Figure 12‑8. Notez que Jamovi trace une ligne à travers les points, nous y reviendrons un peu plus loin dans la section 12.3. Le tracé d’un nuage de points de cette façon vous permet également de spécifier des « densités pour les variables » et cette option ajoute une courbe de densité montrant comment les données de chaque variable sont réparties.

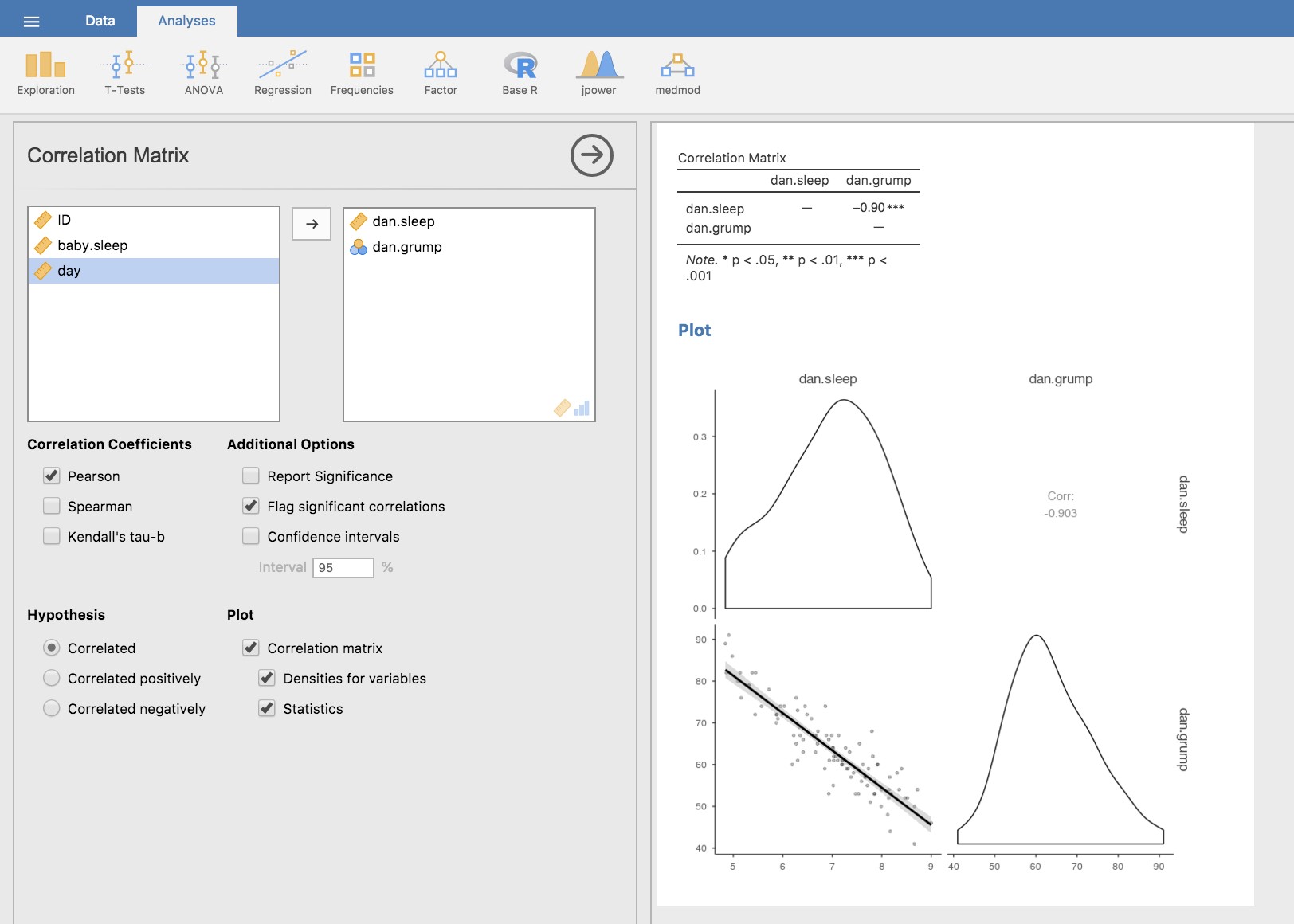
Figure 12‑8 : Diagramme de dispersion via la commande « Correlation Matrix » dans Jamovi

La deuxième façon de faire est d’utiliser l’un des modules complémentaires Jamovi. Ce module s’appelle « Scatr » et vous pouvez l’installer en cliquant sur la grande icône « + » en haut à droite de l’écran Jamovi, en ouvrant la bibliothèque Jamovi, en faisant défiler vers le bas jusqu’à trouver « scatr » et en cliquant sur « Install ». Une fois que vous avez fait cela, vous trouverez une nouvelle commande « Scatterplot » disponible sous le bouton « Exploration ». Ce graphique est un peu différent de la première façon, voir la Figure 12‑9, mais l’information importante est la même.

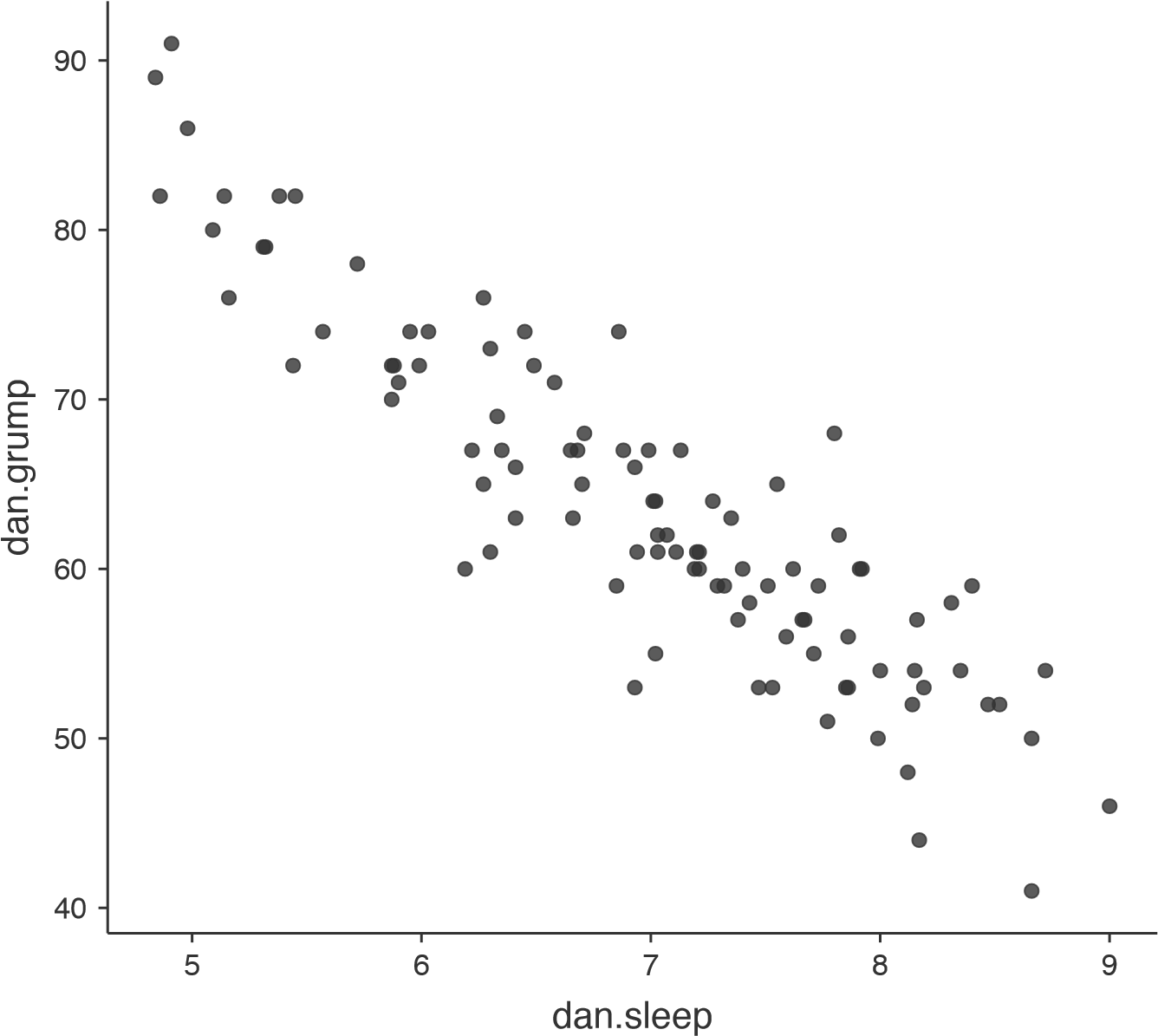
Figure 12‑9 : Diagramme de dispersion via le module additionnel « Scatr » dans Jamovi

12.2.1 Des options plus élaborées

Souvent, vous voudrez examiner les relations entre plusieurs variables à la fois, en utilisant une matrice de nuage de points (dans Jamovi via la commande « Correlation Matrix » - « Plot »). Ajoutez simplement une autre variable, par exemple baby.sleep à la liste des variables à corréler, et Jamovi créera une matrice de nuage de points pour vous, tout comme celle de la Figure 12‑10.

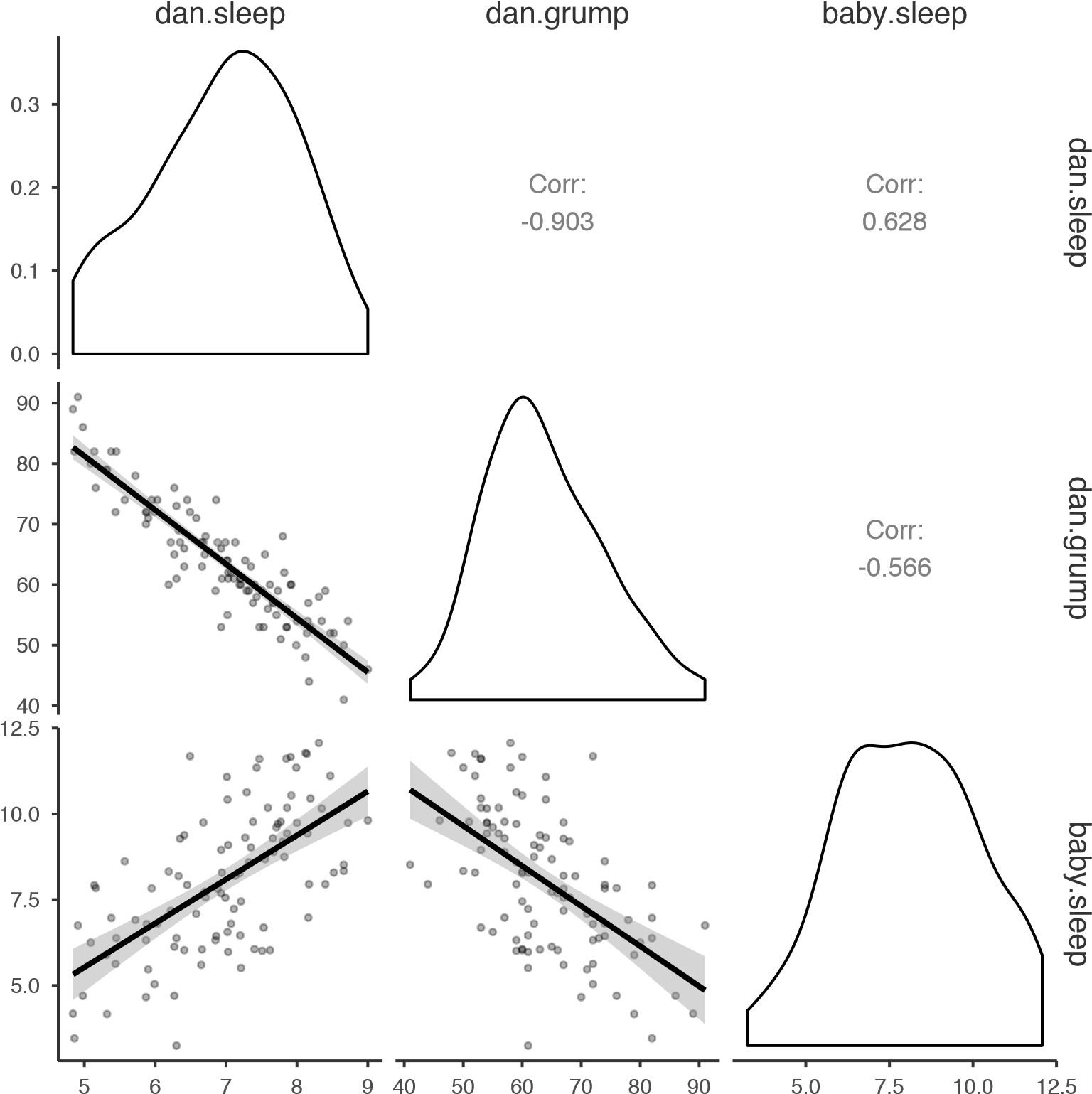
Figure 12‑10 : Une matrice de nuages de points réalisé à l’aide de Jamovi.

12.3 Qu’est-ce qu’un modèle de régression linéaire ?

Les modèles de régression linéaire, réduits à l’essentiel, sont essentiellement une version légèrement plus sophistiquée de la corrélation de Pearson (section 12.1), bien que, comme nous le verrons plus loin, les modèles de régression soient des outils beaucoup plus puissants.

Puisque les idées de base de la régression sont étroitement liées à la corrélation, nous reviendrons au fichier parenthood.csv que nous utilisions pour illustrer le fonctionnement des corrélations. Rappelons que, dans cet ensemble de données, nous essayions de découvrir pourquoi Dan est si grincheux tout le temps et notre hypothèse de travail était que je ne dors pas assez. Nous avons dessiné quelques nuages de points pour nous aider à examiner la relation entre la quantité de sommeil que j’obtiens et ma mauvaise humeur le lendemain, comme dans la Figure 12‑9, et comme nous l’avons vu précédemment cela correspond à une corrélation de r=-0,90, mais ce que nous imaginons secrètement est quelque chose qui ressemble davantage à la Figure 12‑11a. C’est-à-dire que nous traçons mentalement une ligne droite au milieu des données. En statistique, cette ligne que nous traçons s’appelle une ligne de régression. Notez que, puisque nous ne sommes pas des idiots, la ligne de régression passe au milieu des données. Nous ne nous trouvons pas à imaginer quoi que ce soit qui ressemble à l’intrigue plutôt stupide illustrée à la Figure 12‑11b.

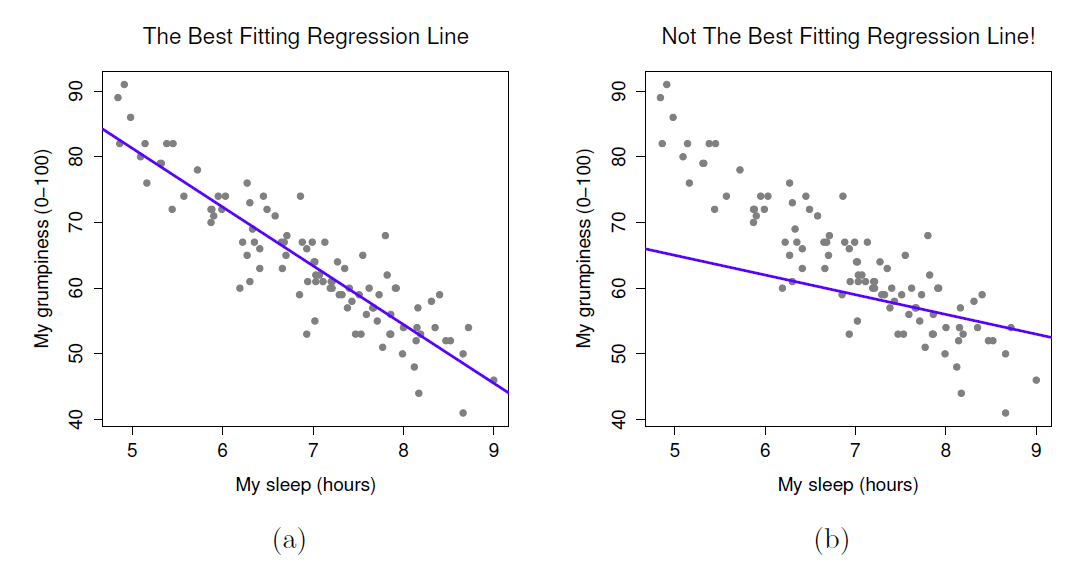
Figure 12‑11: La figure (a) montre le diagramme de dispersion du sommeil de la Figure 12‑9 avec la ligne de régression la mieux adaptée tracée au-dessus du sommet. Comme on pouvait s’y attendre, la ligne passe au milieu des données. En revanche, la figure(b) montre les mêmes données, mais avec un très mauvais choix de ligne de régression tracée par-dessus.

Ce n’est pas très surprenant. La ligne que j’ai tracée dans la Figure 12‑11b ne correspond pas très bien aux données, donc il n’est pas très logique de la proposer comme moyen de résumer les données. C’est une observation très simple à faire, mais elle s’avère très puissante lorsqu’on commence à essayer de l’entourer d’un peu de mathématiques. Pour ce faire, commençons par un rafraîchissement de quelques notions mathématiques du secondaire. La formule pour une ligne droite est généralement écrite comme ceci

\[y=a+bx\]

Ou, du moins, c’est ce que c’était quand je suis allé au lycée, il y a longtemps. Les deux variables sont x et y, et nous avons deux coefficients, a et b.⁹⁶ Le coefficient a représente l’intersection y de la ligne, et le coefficient b représente la pente de la ligne. En remontant plus loin dans nos souvenirs délabrés du lycée (désolé, pour certains d’entre nous, le lycée c’était il y a longtemps), nous nous souvenons que l’intersection est interprétée comme « la valeur de y que l’on obtient quand x=0 »⁹⁷. De même, une pente de b signifie que si vous augmentez la valeur x de 1 unité, alors la valeur y augmente de b unités, et une pente négative signifie que la valeur y diminuerait au lieu de monter. Mais bien sûr, tout me revient. Maintenant que nous nous sommes rappelés qu’il ne faut pas s’étonner de découvrir que nous utilisons exactement la même formule pour une droite de régression. Si Y est la variable résultat (la VD) et X est la variable prédictive (la VI), alors la formule qui décrit notre régression s’écrit comme suit

\[ {\hat{Y}}_{i} = b_{0} + b_{1}X_{i} \] Bien. Ça ressemble à la même formule, mais il y a quelques petits morceaux de plus dans cette version. Assurons-nous de les comprendre. Tout d’abord, remarquez que j’ai écrit X_i et Y_i plutôt que simplement X et Y. C’est parce que nous voulons nous rappeler qu’il s’agit de données réelles. Dans cette équation, X_i est la valeur de la variable prédictive pour la i-ième observation (c.-à-d. le nombre d’heures de sommeil que j’ai eues le premier jour de ma petite étude) et Y_i est la valeur correspondante de la variable résultat (c.-à-d. ma mauvaise humeur ce jour-là). Et bien que je ne l’ai pas dit aussi explicitement dans l’équation, ce que nous supposons, c’est que cette formule fonctionne pour toutes les observations de l’ensemble des données (c.-à-d. pour tout i). Deuxièmement, remarquez que j’ai écrit \({\hat{Y}}_{i}\) et non Y_i. C’est parce que nous voulons faire la distinction entre les données réelles Y_i et l’estimation \({\hat{Y}}_{i}\) (c.-à-d. la prévision que fait notre ligne de régression). Troisièmement, j’ai changé les lettres utilisées pour décrire les coefficients de a et b à b0 et b1. C’est exactement la façon dont les statisticiens aiment se référer aux coefficients dans un modèle de régression. Je ne sais pas pourquoi ils ont choisi b, mais c’est ce qu’ils ont fait. Dans tous les cas, b₀ se réfère toujours au terme d’intersection et b₁ à la pente.

Excellent !. Ensuite, je ne peux m’empêcher de remarquer, qu’il s’agisse de la bonne ou de la mauvaise ligne de régression, que les données ne tombent pas parfaitement sur la ligne. Ou, pour le dire autrement, les données Y_i ne sont pas identiques aux prédictions du modèle de régression \({\hat{Y}}_{i}\). Puisque les statisticiens aiment attacher des lettres, des noms et des chiffres à tout, considérons la différence entre la prédiction du modèle et les données réelles résidu, et nous l’appellerons \(\epsilon_{i}\). En écriture mathématique, les résidus sont définis comme suit

\[ \epsilon_{i} = Y_{i} - {\hat{Y}}_{i} \]

ce qui signifie que nous pouvons écrire le modèle de régression linéaire complet comme suit

\[ Y_{i} = b_{0} + b_{1}X_{i} + \epsilon_{i} \]

12.4 Estimation d’un modèle de régression linéaire

Bien, maintenant redessinons nos graphiques mais cette fois j’ajouterai quelques lignes pour montrer la taille du résidu pour toutes les observations. Lorsque la ligne de régression est bonne, nos résidus (la longueur des lignes noires pleines) semblent tous assez petits, comme le montre la Figure 12‑12a, mais lorsque la ligne de régression est mauvaise, les résidus sont beaucoup plus grands, comme vous pouvez le voir à la Figure 12‑12b.

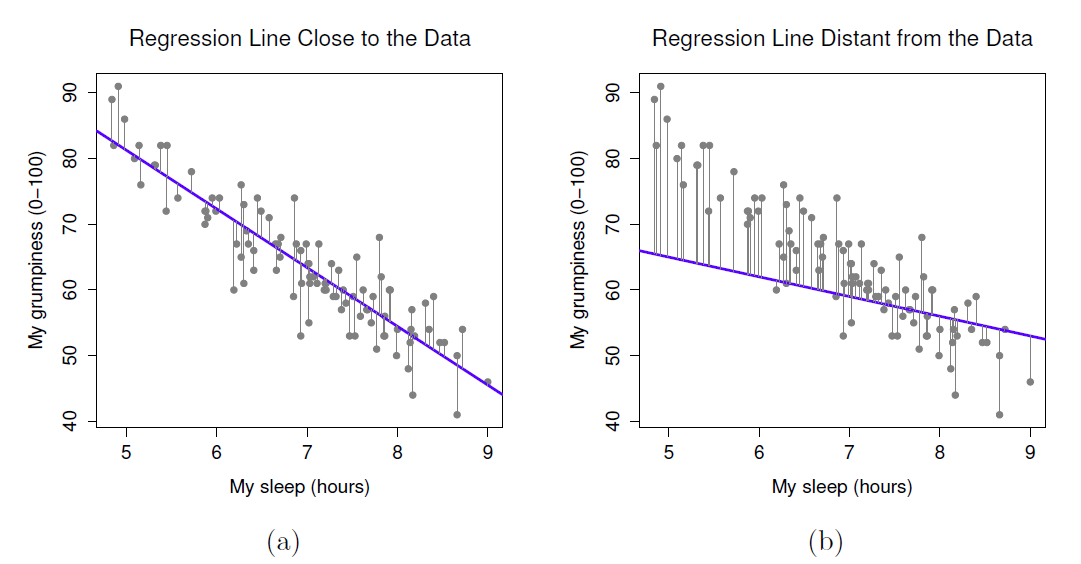
Figure 12‑12 : Représentation des résidus associés à la droite de régression la mieux adaptée (figure a) et des résidus associés à une droite de régression faible (figure b). Les résidus sont beaucoup plus petits pour la bonne ligne de régression. Encore une fois, ce n’est pas surprenant étant donné que la bonne ligne est celle qui passe en plein milieu des données.

Bon. Peut-être que ce que nous « voulons » dans un modèle de régression, ce sont de petits résidus. Oui, cela semble logique. En fait, je pense aller jusqu’à dire que la ligne de régression « la mieux adaptée » est celle qui a le moins de résidus. Ou, mieux encore, puisque les statisticiens semblent aimer prendre des carrés de tout, pourquoi ne pas le dire :

Les coefficients de régression estimés, \({\hat{b}}_{0}\) et \({\hat{b}}_{1}\), sont ceux qui minimisent la somme des résidus au carré, que l’on peut écrire soit \(\sum_{i}^{}\left( Y_{i}-{\hat{Y}}_{i}\right)^{2}\), soit \(\sum_{i}^{}\epsilon_{i}^{2}\).

Bien, ça sonne encore mieux. Et comme je l’ai détaillé comme ça, ça veut probablement dire que c’est la bonne réponse. Et comme c’est la bonne réponse, il vaut probablement la peine de noter que nos coefficients de régression sont des estimations (nous essayons de deviner les paramètres qui décrivent une population !), c’est pourquoi j’ai ajouté les petits chapeaux, pour obtenir \({\hat{b}}_{0}\) et \({\hat{b}}_{1\ }\) plutôt que b₀ et b₁. Enfin, comme il existe en fait plus d’une façon d’estimer un modèle de régression, le nom plus technique de ce processus d’estimation est régression des moindres carrés ordinaires (MCO).

A ce stade, nous avons maintenant une définition concrète de ce qui constitue notre « meilleur » choix de coefficients de régression, \({\hat{b}}_{0}\) et \({\hat{b}}_{1\ }\). La question naturelle à se poser ensuite est la suivante : si nos coefficients de régression optimaux sont ceux qui minimisent la somme des résidus au carré, comment pouvons-nous trouver ces merveilleux nombres ? La réponse à cette question est compliquée et ne vous aide pas à comprendre la logique de la régression.⁹⁸ Cette fois, je vais vous laisser tranquille. Au lieu de vous montrer le chemin long et fastidieux d’abord et de « révéler » ensuite le merveilleux raccourci que fournit Jamovi, allons droit au but et utilisons juste Jamovi pour faire tout le travail lourd.

12.4.1 Régression linéaire dans Jamovi

Pour exécuter la régression linéaire, ouvrez l’analyse « Regression » - « Linear Regression » dans Jamovi, en utilisant le fichier de données parenthood.csv. Spécifiez ensuite dan.grump comme variable dépendante et dan.sleep comme variable entrée dans la case « Covariables ». Ceci donne les résultats illustrés à la Figure 12.13, montrant une interception \({\hat{b}}_{0} = 125,96\) et la pente \({\hat{b}}_{1} = - 8,94\). En d’autres termes, la ligne de régression la mieux adaptée que j’ai tracée à la figure 12.11 a cette formule :

\[ {\hat{Y}}_{i} = 125,96 + ( - 8,94 X_{i}) \]

12.4.2 Interprétation du modèle estimé

La chose la plus importante à comprendre est de savoir comment interpréter ces coefficients. Commençons par \({\hat{b}}_{1}\), la pente. Si l’on se souvient de la définition de la pente, un coefficient de régression de \({\hat{b}}_{1} = - 8,94\) signifie que si j’augmente X_i de 1, alors je diminue Y_i de 8,94. C’est-à-dire, chaque heure supplémentaire de sommeil que je améliorer mon humeur en réduisant ma grinchiosité de 8,94 points. Et l’intersection ? Eh bien, puisque \({\hat{b}}_{0}\) correspond à « la valeur attendue de Y_i quand X_i est égal à 0 », c’est assez simple. Cela implique que si j’obtiens zéro heure de sommeil (X_i=0) alors ma grinchiosité va monter en flèche, à une valeur folle de (Y_i=125,96). Il vaut mieux l’éviter, je crois.

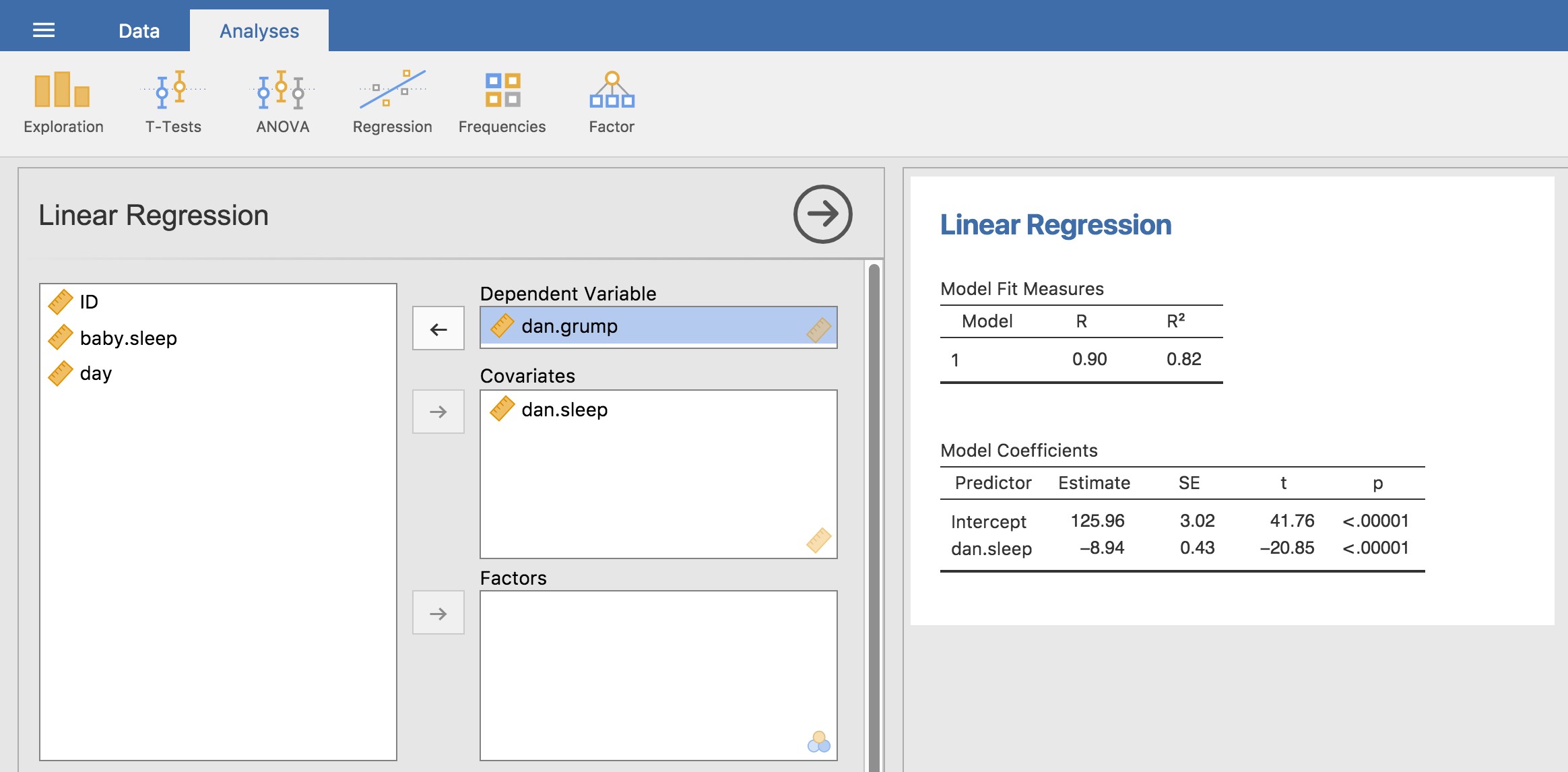
Figure 12‑13 : Une capture d’écran de Jamovi montrant une analyse de régression linéaire simple.

12.5 Régression linéaire multiple

Le modèle de régression linéaire simple dont nous avons discuté jusqu’à présent suppose qu’il y a une seule variable prédictive qui vous intéresse, en l’occurrence dan.sleep. En fait, jusqu’à maintenant, tous les outils statistiques dont nous avons parlé ont supposé que votre analyse utilise une variable prédictive et une variable résultat. Cependant, dans de nombreux projets de recherche (peut-être la plupart), vous avez en fait de multiples prédicteurs que vous voulez examiner. Dans l’affirmative, il serait bon de pouvoir étendre le cadre de régression linéaire pour pouvoir inclure de multiples prédicteurs. Peut-être un modèle de régression multiple serait-il nécessaire ?

La régression multiple est conceptuellement très simple. Tout ce que nous faisons, c’est d’ajouter d’autres termes à notre équation de régression. Supposons que nous ayons deux variables qui nous intéressent ; peut-être voulons-nous utiliser dan.sleep et baby.sleep pour prédire la variable dan.grump. Comme avant, nous laissons Y_i se représenter à ma grinchiosité le i-ème jour. Mais maintenant nous avons deux variables X : la première correspondant à la quantité de sommeil que j’ai eu et la seconde correspondant à la quantité de sommeil que mon fils a eu. Nous avons donc X_i1 qui correspond aux heures pendant lesquelles j’ai dormi le i-ème jour et X_i2 aux heures pendant lesquelles le bébé a dormi ce jour-là. Si c’est le cas, alors nous pouvons écrire notre modèle de régression comme ceci :

\[ Y_{i} = b_{0} + b_{1}X_{i1} + b_{2}X_{i2} + \epsilon_{i} \]

Comme précédemment, \(\epsilon_{i}\) est le résidu associé à la i-ème observation, \(\epsilon_{i} = Y_{i} - {\hat{Y}}_{i}\). Dans ce modèle, nous avons maintenant trois coefficients à estimer : b₀ est l’interception, b₁ est le coefficient associé à mon sommeil et b₂ est le coefficient associé au sommeil de mon fils. Cependant, bien que le nombre de coefficients à estimer ait changé, l’idée de base du fonctionnement de l’estimation reste inchangée : nos coefficients estimés \({\hat{b}}_{0}\), \({\hat{b}}_{1}\)et \({\hat{b}}_{2}\) sont ceux qui minimisent la somme des carrés des résidus.

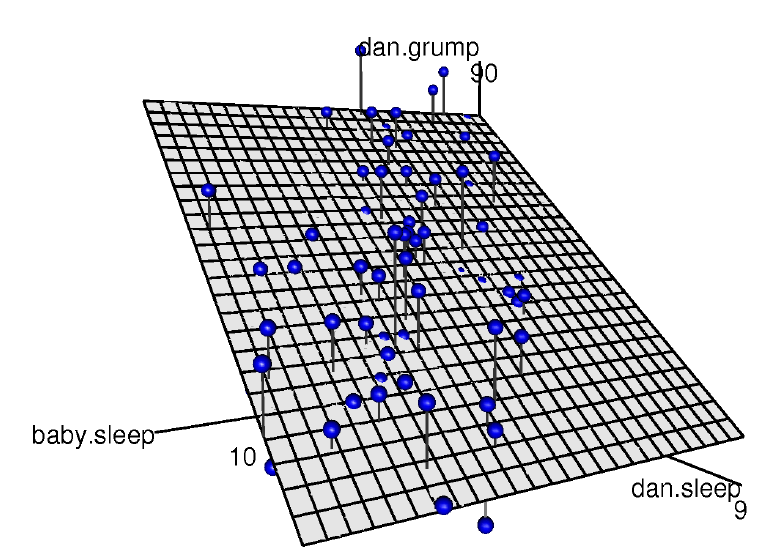
Figure 12‑14 : Visualisation 3D d’un modèle de régression multiple. Il y a deux prédicteurs dans le modèle, dan.sleep et baby.sleep, et la variable de résultat est dan.grump. Ensemble, ces trois variables forment un espace 3D. Chaque observation (point) est un point dans cet espace. De la même manière qu’un modèle de régression linéaire simple forme une ligne dans un espace 2D, ce modèle de régression multiple forme un plan dans un espace 3D. Lorsque nous estimons les coefficients de régression, nous essayons de trouver un plan aussi proche que possible de tous les points bleus.

12.5.1 Le faire avec Jamovi

La régression multiple dans Jamovi n’est pas différente de la régression simple. Tout ce que nous avons à faire est d’ajouter des variables supplémentaires à la boîte « Covariables » dans Jamovi. Par exemple, si nous voulons utiliser dan.sleep et baby.sleep comme prédicteurs dans notre tentative d’expliquer pourquoi je suis si grincheux, alors déplacez baby.sleep dans la case « Covariables » à côté de dan.sleep. Par défaut, Jamovi suppose que le modèle doit inclure une intersection. Les coefficients que nous obtenons cette fois-ci sont :

(Intersection)	dan.sleep	baby.sleep
125.97	-8.95	.01

Le coefficient associé à dan.sleep est assez élevé, ce qui suggère que chaque heure de sommeil que je perds me rend beaucoup plus grincheux. Cependant, le coefficient pour baby.sleep est très faible, ce qui suggère que le temps de sommeil de mon fils n’a pas vraiment d’importance. Ce qui compte pour moi, c’est de savoir combien de temps je dors. Pour avoir une idée de ce à quoi ressemble ce modèle de régression multiple, la Figure 12‑14 montre un graphique 3D qui trace les trois variables, ainsi que le modèle de régression lui-même.

12.5.2 Formule pour le cas général

L’équation que j’ai donnée ci-dessus vous montre à quoi ressemble un modèle de régression multiple lorsque vous incluez deux prédicteurs. Il n’est donc pas surprenant que si vous voulez plus de deux prédicteurs, il vous suffit d’ajouter plus de termes X et plus de coefficients b. En d’autres termes, si vous avez K prédicteur dans le modèle, l’équation de régression se présente comme suit

\[Y_{i} = b_{0} + \left( \sum_{k = 1}^{k}{b_{k}X_{\text{ik}}} \right) + \epsilon_{i}\]

12.6 Quantifier l’ajustement du modèle de régression

Nous savons donc maintenant comment estimer les coefficients d’un modèle de régression linéaire. Le problème est que nous ne savons pas encore si ce modèle de régression est bon. Par exemple, le modèle de régression.1 prétend que chaque heure de sommeil améliorera considérablement mon humeur, mais il se peut que ce soit de la foutaise. Rappelez-vous que le modèle de régression ne produit qu’une prédiction \({\hat{Y}}_{i}\) sur mon humeur, mais mon humeur réelle est Y_i. Si ces deux éléments sont très proches, le modèle de régression marche bien. S’ils sont très différents, c’est qu’il ne marche pas.

12.6.1 La valeur R²

Encore une fois, enveloppons d’un peu de mathématiques cela. Tout d’abord, nous avons la somme des résidus au carré dont nous espérons qu’il sera plutôt petit.

\[ \text{SS}_{\text{res}} = \sum_{i}^{}\left( Y_{i} - {\hat{Y}}_{i} \right)^{2} \]

Plus précisément, ce que nous aimerions, c’est qu’il soit très faible par rapport à la variabilité totale de la variable résultats

\[ \text{SS}_{\text{tot}} = \sum_{i}^{}\left( Y_{i} - \bar{Y} \right)^{2} \]

Pendant que nous y sommes, calculons ces valeurs, mais pas à la main. Utilisons quelque chose comme Excel ou un autre tableur standard. J’ai fait ceci en ouvrant le fichier parenthood.csv dans Excel et en l’enregistrant comme parenthood rsquared.xls pour que je puisse travailler dessus. La première chose à faire est de calculer les valeurs de \(\hat{Y}\), et pour le modèle simple qui n’utilise qu’un seul prédicteur, nous ferions ce qui suit :

1. créer une nouvelle colonne appelée « Y.pred » en utilisant la formule « = 125,97 + (-8,94 * dan.sleep) ».

Bien, maintenant que nous avons une variable qui stocke les prédictions du modèle de régression afin de savoir à quel point je serai grincheux un jour donné, calculons notre somme des résidus au carré. Pour ce faire, nous utiliserions la formule suivante :

1. calculer la SSres en créant une nouvelle colonne appelée « (Y-Y.pred)^2 » en utilisant la formule « = (dan.grump - Y.pred)^2 ».

2. Ensuite, au bas de cette colonne, calculez la somme de ces valeurs, i.e.’sum((Y-Y.pred)^2).

Ceci devrait vous donner une valeur de « 1838.722 ». Merveilleux. Un gros chiffre qui ne veut pas dire grand-chose. Néanmoins, allons quand même de l’avant avec audace et calculons aussi la somme totale des carrés. C’est aussi assez simple. Calculez la SS(tot) par :

4. Au bas de la colonne dan.grump, calculez la valeur moyenne pour dan.grump (NB Excel utilise le mot « MOYENNE » dans sa fonction).

5. Créez ensuite une nouvelle colonne, appelée « (Y - mean(Y))^2 ) » en utilisant la formule « = (dan.grump - AVERAGE(dan.grump))^2 ».

6. Ensuite, au bas de cette colonne, calculez la somme de ces valeurs, C’est-à-dire « somme((Y - moyenne(Y))^2) ».

Ceci devrait vous donner une valeur de « 9998.59 ». Bien, il s’agit d’un nombre beaucoup plus élevé que le précédent, ce qui donne à penser que notre modèle de régression fait de bonnes prédictions. Mais ce n’est pas très interprétable.

On peut peut-être arranger ça. Ce que nous aimerions faire, c’est convertir ces deux chiffres plutôt insignifiants en un seul chiffre. Un joli chiffre interprétable, que nous appellerons R² sans raison particulière. Ce que nous aimerions, c’est que la valeur de R² soit égale à 1 si le modèle de régression ne fait aucune erreur de prédiction des données. En d’autres termes, s’il s’avère que les erreurs résiduelles sont nulles. De même, si le modèle est complètement inutile, nous voudrions que R² soit égal à 0. Qu’est-ce que j’entends par « inutile » ? Aussi tentant que cela puisse paraître d’exiger que le modèle de régression quitte la maison, se coupe les cheveux et trouve un vrai emploi, je vais probablement devoir choisir une définition plus pratique. Dans ce cas, tout ce que je veux dire, c’est que la somme résiduelle des carrés n’est pas inférieure à la somme totale des carrés, SSres = SStot. Attendez, pourquoi ne pas faire exactement ça ? La formule qui nous fournit notre valeur R² est assez simple à écrire,

\[ R^{2} = 1 - \frac{\text{SS}_{\text{res}}}{\text{SS}_{\text{tot}}} \]

et tout aussi simple à calculer dans Excel :

7. Calculez R.au carré en tapant dans une case vide ce qui suit : « =1 - (SS(resid) / SS(tot) ) ».

Ceci donne une valeur pour R² de 0,8161018. La valeur R², parfois appelée coefficient de détermination,⁹⁹ a une interprétation simple : c’est la proportion de la variance de la variable résultat qui peut être prise en compte par le prédicteur. Donc, dans ce cas, le fait que nous ayons obtenu R²=0,816 signifie que le prédicteur (my.sleep) explique 81,6% de la variance du résultat (my.grump).

Naturellement, vous n’avez pas besoin de taper toutes ces commandes vous-même dans Excel si vous voulez obtenir la valeur R² pour votre modèle de régression. Comme nous le verrons plus loin dans Section 12.7.3, tout ce que vous avez à faire est de le spécifier comme option dans Jamovi. Cependant, mettons cela de côté pour l’instant. Il y a une autre propriété de R² que je tiens à souligner.

12.6.2 La relation entre régression et corrélation

À ce stade, nous pouvons revenir sur mon affirmation antérieure selon laquelle la régression, sous cette forme très simple dont j’ai parlé jusqu’ici, est essentiellement la même chose qu’une corrélation. Auparavant, nous utilisions le symbole r pour désigner une corrélation de Pearson. Pourrait-il y avoir une relation entre la valeur du coefficient de corrélation r et la valeur R² de la régression linéaire ? Bien sûr qu’il y en a : la corrélation au carré r² est identique à la valeur R² pour une régression linéaire avec un seul prédicteur. En d’autres termes, l’exécution d’une corrélation de Pearson équivaut plus ou moins à l’exécution d’un modèle de régression linéaire qui utilise une seule variable prédictive.

12.6.3 La valeur R² ajustée

Une dernière chose à souligner avant de passer à autre chose. Il est assez courant pour les gens de rapporter une mesure légèrement différente de la performance du modèle, connue sous le nom de « R² ajusté ». La motivation qui sous-tend le calcul de la valeur corrigée de R² est l’observation que l’ajout d’autres variables prédictrices dans le modèle entraînera toujours une augmentation (ou au moins pas de diminution) de la valeur de R².

La valeur R² ajustée introduit une légère modification dans le calcul, comme suit. Pour un modèle de régression avec K prédicteurs, ajusté à un ensemble de données contenant N observations, le R² ajusté est :

\[ \text{adj.}R^{2} = 1 - \frac{\text{SS}_{\text{res}}}{\text{SS}_{\text{tot}}} \times \frac{N - 1}{N - K - 1} \]

Cet ajustement est une tentative de prise en compte des degrés de liberté. Le grand avantage de la valeur corrigée de R² est que lorsque vous ajoutez plus de prédicteurs au modèle, la valeur corrigée de R² n’augmentera que si les nouvelles variables améliorent la performance du modèle plus que vous ne l’attendriez par hasard. Le grand inconvénient est que la valeur R² ajustée ne peut pas être interprétée de la même manière élégante que R². R² a une interprétation simple, c’est la proportion de variance dans la variable résultats qui s’explique par le modèle de régression. A ma connaissance, il n’existe pas d’interprétation équivalente pour le R² ajusté.

Une question évidente est donc de savoir si vous devez déclarer R² ou R² ajusté. C’est probablement une question de préférence personnelle. Si vous vous souciez davantage de l’interprétabilité, alors R² est meilleur. Si vous vous souciez davantage de corriger les biais, alors R² ajusté est probablement mieux. Pour ma part, je préfère R². J’ai l’impression qu’il est plus important d’être capable d’interpréter la mesure de la performance de votre modèle. De plus, comme nous le verrons à la section 12.7, si vous craignez que l’amélioration de R² que vous obtenez en ajoutant un prédicteur ne soit due qu’au hasard et non à un meilleur modèle, nous avons des tests d’hypothèse pour cela.

12.7 Tests d’hypothèse pour les modèles de régression

Jusqu’à présent, nous avons parlé de ce qu’est un modèle de régression, de la façon dont les coefficients d’un modèle de régression sont estimés et de la façon dont nous quantifions le rendement du modèle (le dernier de ces éléments, soit dit en passant, est essentiellement notre mesure de la valeur de l’effet). La prochaine chose dont nous devons parler, c’est des tests d’hypothèse. Il y a deux types de tests d’hypothèse différents (mais apparentés) dont nous devons parler : ceux dans lesquels nous vérifions si le modèle de régression dans son ensemble donne de bien meilleurs résultats qu’un modèle basé sur l’hypothèse nulle, et ceux dans lesquels nous vérifions si un coefficient de régression particulier est sensiblement différent de zéro.

12.7.1 Tester le modèle dans son ensemble

Supposons que vous ayez estimé votre modèle de régression. Le premier test d’hypothèse que vous pouvez essayer est l’hypothèse nulle qu’il n’y a pas de relation entre les prédicteurs et le résultat, et l’hypothèse alternative que les données sont distribuées exactement comme le modèle de régression le prévoit.

Formellement, notre « modèle correspondant à l’hypothèse nulle » correspond au modèle de « régression » assez trivial dans lequel nous incluons 0 prédicteurs et n’incluons que le terme d’intersection b₀ :

\[ H_{0}:Y_{i} = b_{0} + \epsilon_{i} \]

Si notre modèle de régression a des k prédicteurs, le « modèle alternatif » est décrit à l’aide de la formule habituelle pour un modèle de régression multiple :

\[ H_{1}:Y_{i} = b_{0} + \left( \sum_{k = 1}^{K}{b_{k}X_{\text{ik}}} \right) + \epsilon_{i} \]

Comment tester ces deux hypothèses l’une par rapport à l’autre ? L’astuce est de comprendre qu’il est possible de diviser la variance totale SS_tot en la somme de la variance résiduelle SS_res et la variance du modèle de régression SS_mod. Je vais sauter les détails techniques, puisque nous y reviendrons plus tard lorsque nous examinerons l’analyse de variance au chapitre 13. Mais notez juste que \[ \text{SS}_{\text{mod}}=\text{text{SS}}_{tot}-\text{SS}_{\text{res}} \]

Et nous pouvons convertir les sommes des carrés en carrés moyens en divisant par les degrés de liberté.

\[ \text{MS}_{\text{mod}} = \frac{\text{SS}_{\text{mod}}}{\text{ddl}_{\text{mod}}} \]

\[ \text{MS}_{\text{res}} = \frac{\text{SS}_{\text{res}}}{\text{ddl}_{\text{res}}} \]

Alors, combien de degrés de liberté avons-nous ? Comme vous pouvez vous y attendre, le df associé au modèle est étroitement lié au nombre de prédicteurs que nous avons inclus. En fait, il s’avère que df_mod=K. Pour les résidus, le degré total des degrés de liberté est df_res=N–K-1.

Maintenant que nous avons nos carrés moyens, nous pouvons calculer une statistique F comme ceci :

\[ F = \frac{\text{MS}_{\text{mod}}}{\text{MS}_{\text{res}}} \]

Nous verrons beaucoup plus de statistiques F au chapitre 13, mais pour l’instant, sachez simplement que nous pouvons interpréter de grandes valeurs F comme indiquant que l’hypothèse nulle fonctionne mal par rapport à l’hypothèse alternative. Dans un instant, je vais vous montrer comment faire le test avec Jamovi de la manière la plus simple, mais voyons d’abord les tests pour les coefficients de régression individuels.

12.7.2 Essais pour les coefficients individuels

Le test F que nous venons de présenter est utile pour vérifier que le modèle dans son ensemble fonctionne mieux que le hasard. Si votre modèle de régression ne produit pas un résultat significatif pour le test F, vous n’avez probablement pas un très bon modèle de régression (ou, très probablement, vous n’avez pas de très bonnes données). Cependant, bien que l’échec à ce test soit un indicateur assez fort que le modèle a des problèmes, le fait de réussir le test (c.-à-d. de rejeter l’hypothèse nulle) ne signifie pas que le modèle est bon ! Vous vous demandez peut-être pourquoi ? La réponse à cette question peut être trouvée en examinant les coefficients du modèle de régression multiple que nous avons déjà regardés à la section 12.5 ci-dessus, où nous avons obtenu les coefficients :

(Intersection)	dan.sleep	baby.sleep
125,97	-8,950	0,01

Je ne peux m’empêcher de remarquer que le coefficient de régression estimé pour la variable baby.sleep est minuscule (0,01), par rapport à la valeur que nous obtenons pour dan.sleep (-8,95). Étant donné que ces deux variables sont absolument sur la même échelle (elles sont toutes deux mesurées en « heures de sommeil »), je trouve cela éclairant. En fait, je commence à soupçonner que c’est seulement la quantité de sommeil que j’obtiens qui compte pour prédire ma grinchiosité.

Nous pouvons réutiliser un test d’hypothèse dont nous avons parlé plus tôt, le test t. Le test qui nous intéresse a pour hypothèse nulle que le vrai coefficient de régression est zéro (\(b = 0\)), qui doit être testé contre l’hypothèse alternative qu’il n’est pas (\(b \neq 0\)). C’est-à-dire :

\[ \text{H}_{0} : b=0\\ \text{H}_{1} : b\neq0 \]

Comment pouvons-nous le tester ? Eh bien, si le théorème central limite est correct, nous pouvons deviner que la distribution d’échantillonnage de \(\hat{b}\), le coefficient de régression estimé, est une distribution normale avec une moyenne centrée sur b. Cela signifie est que si l’hypothèse nulle était vraie, alors la distribution d’échantillonnage de \(\hat{b}\) a une moyenne nulle et un écart type inconnu. En supposant que nous puissions obtenir une bonne estimation de l’erreur type du coefficient de régression, \(\text{SE}\left( \hat{b} \right)\), alors nous avons de la chance. C’est exactement la situation pour laquelle nous avons introduit le test t sur un échantillon au chapitre 11. Définissons donc une statistique t comme ceci

\[ t = \frac{\hat{b}}{\text{SE}\left( \hat{b} \right)} \]

Je vais sauter les justifications, mais nos degrés de liberté dans ce cas sont df=N-K-1.

Il est irritant de constater que l’estimation de l’erreur type du coefficient de régression, \(\text{SE}\left( \hat{b} \right)\), n’est pas aussi facile à calculer que l’erreur type de la moyenne que nous avons utilisée pour les tests t plus simples au chapitre 11. En fait, la formule est quelque peu laide et n’est pas très utile à regarder.¹⁰⁰ Pour nos besoins, il suffit de souligner que l’erreur type du coefficient de régression estimé dépend à la fois du prédicteur et des variables de résultat, et qu’elle est quelque peu sensible aux violations de l’hypothèse d’homogénéité de la variance (examinée plus loin).

En tout état de cause, cette statistique t peut être interprétée de la même manière que les statistiques t dont nous avons parlé au chapitre 11. En supposant que vous avez une hypothèse alternative bilatérale (c’est-à-dire que vous ne vous souciez pas vraiment de savoir si b < 0 ou b > 0), alors ce sont les valeurs extrêmes de t (c’est-à-dire beaucoup moins que zéro ou beaucoup plus que zéro) qui suggèrent que vous devez rejeter l’hypothèse nulle.

12.7.3 Exécuter les tests d’hypothèse dans Jamovi

Pour calculer toutes les statistiques dont nous avons parlé jusqu’à présent, tout ce que vous avez à faire est de vous assurer que les options pertinentes sont cochées dans Jamovi et ensuite exécuter la régression. Si nous faisons cela, comme le montre la Figure 12‑15, nous obtenons toute une série de résultats utiles.

Les « coefficients du modèle » au bas des résultats de l’analyse de Jamovi présentés à la Figure 12‑15 fournissent les coefficients du modèle de régression. Chaque ligne de ce tableau fait référence à l’un des coefficients du modèle de régression. La première ligne est le terme d’intersection, et les dernières lignes regardent chacun des prédicteurs. Les colonnes vous donnent toutes les informations pertinentes. La première colonne est l’estimation réelle de b (p. ex. 125,97 pour l’intersection et -8,95 pour le prédicteur dan.sleep). La deuxième colonne est l’estimation de l’erreur type \({\hat{\sigma}}_{b}\). Les troisième et quatrième colonnes fournissent les valeurs inférieures et supérieures pour l’intervalle de confiance à 95 % autour de l’estimation b (nous y reviendrons plus loin).

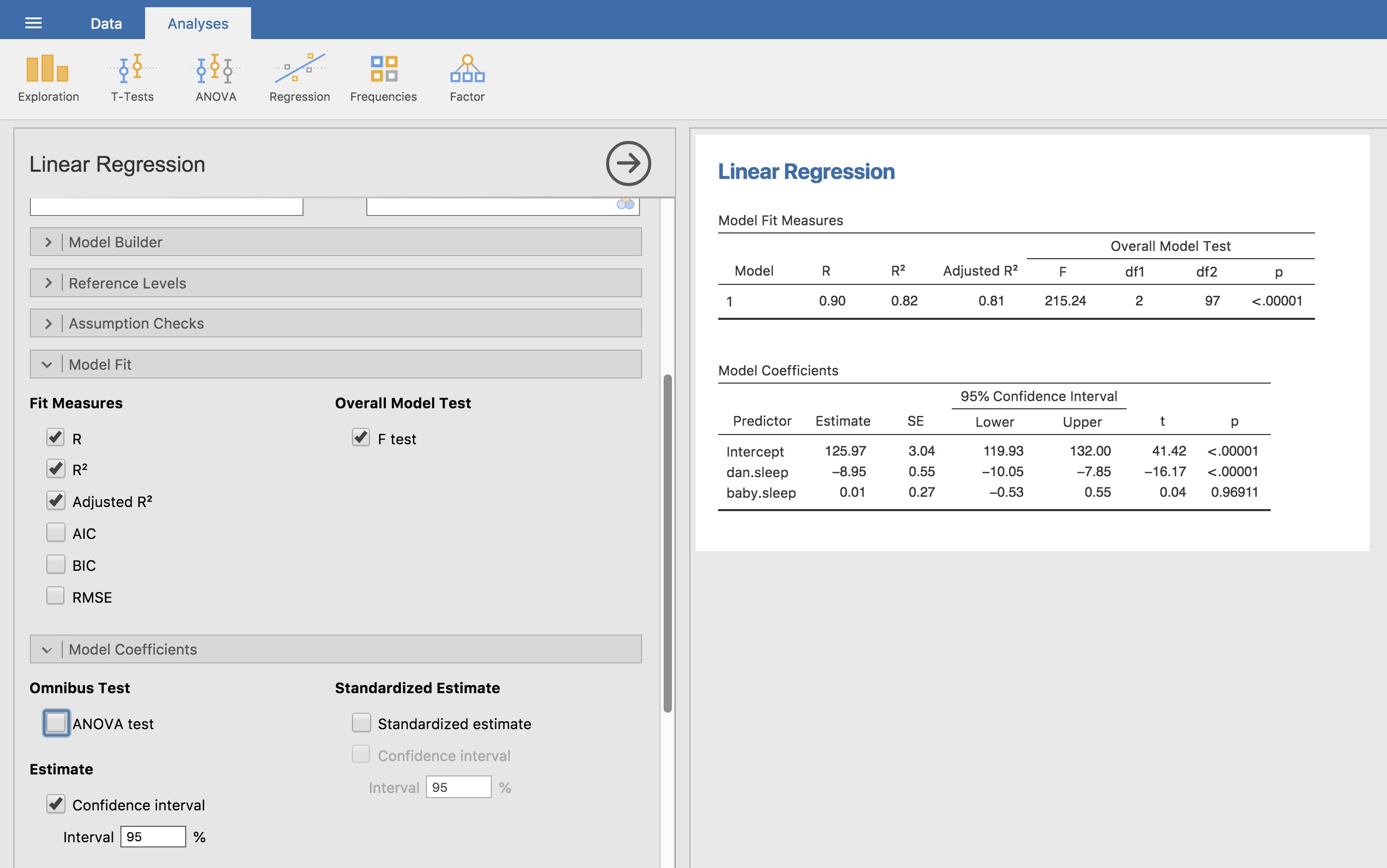
Figure 12‑15 : Une capture d’écran de Jamovi montrant une analyse de régression linéaire multiple, avec quelques options utiles cochées.

La cinquième colonne vous donne la statistique t, et il est intéressant de noter que dans ce tableau \(t = \hat{b}/SE\left( \hat{b} \right)\) à chaque fois. Enfin, la dernière colonne vous donne la valeur p réelle de chacun de ces tests.¹⁰¹

La seule chose que le tableau des coefficients lui-même n’énumère pas est le degré de liberté utilisé dans le test t, qui est toujours N -K-1 et qui est énuméré dans le tableau en haut de la sortie, intitulé « Model Fit Measures ». On peut voir dans ce tableau que le modèle est bien plus performant que ce à quoi on pourrait s’attendre par hasard (F_(2,97)=215,24, p <.001), ce qui n’est pas si surprenant : le R² =0,81 indique que le modèle de régression représente 81 % de la variabilité de la mesure des résultats (et 82 % pour le R² ajusté). Cependant, lorsque nous examinons les tests t pour chacun des coefficients individuels, nous avons des preuves assez solides que la variable baby.sleep n’a pas d’effet significatif. Tout le travail dans ce modèle est effectué par la variable dan.sleep. Pris ensemble, ces résultats suggèrent que ce modèle de régression n’est pas le bon modèle pour les données. Vous feriez probablement mieux de laisser tomber le prédicteur de baby.sleep. En d’autres termes, le modèle de régression simple avec lequel nous avons commencé est le meilleur modèle.

12.8 A propos des coefficients de régression

Avant de discuter des hypothèses qui sous-tendent la régression linéaire et de ce que vous pouvez faire pour vérifier si elles sont respectées, j’aimerais aborder brièvement deux autres sujets, qui ont tous deux trait aux coefficients de régression. La première chose dont il faut parler est le calcul des intervalles de confiance pour les coefficients. Ensuite, j’aborderai la question quelque peu floue de savoir comment déterminer quel prédicteur est le plus important.

12.8.1 Intervalles de confiance pour les coefficients

Comme tout paramètre de population, les coefficients de régression b ne peuvent être estimés avec une précision complète à partir d’un échantillon de données ; c’est en partie pourquoi nous avons besoin de tests d’hypothèse. Par conséquent, il est très utile de pouvoir rapporter des intervalles de confiance qui expriment notre incertitude au sujet de la valeur réelle de b. Cela est particulièrement utile lorsque la question de recherche est fortement axée sur une tentative d’établir la relation entre la variable X et la variable Y, puisque, dans ces situations, l’intérêt se porte principalement sur le coefficient de régression b.

Heureusement, les intervalles de confiance pour les coefficients de régression peuvent être construits de la manière habituelle

\[ \text{CI}\left( b \right) = \hat{b} \pm \left( t_{\text{crit}} \times SE(\hat{b}) \right) \]

où \(SE(\hat{b})\) est l’erreur type du coefficient de régression et t_crit est la valeur critique pertinente de la distribution t appropriée. Par exemple, si c’est un intervalle de confiance à 95 % que nous voulons, alors la valeur critique est le quantile 97,5 d’une distribution t avec N–K-1 degrés de liberté. En d’autres termes, il s’agit essentiellement de la même méthode de calcul des intervalles de confiance que celle que nous avons utilisée jusqu’ici.

Dans Jamovi, nous avions déjà spécifié l’intervalle de confiance à 95 %, comme le montre la Figure 12‑15, bien que nous aurions pu facilement choisir une autre valeur, par exemple un intervalle de confiance à 99 %, si nous l’avion voulu.

12.8.2 Calcul des coefficients de régression standardisés

Vous voudrez peut-être également calculer des coefficients de régression « standardisés », souvent désignés par \(\beta\). La logique derrière les coefficients standardisés est la suivante. Dans de nombreuses situations, vos variables se situent sur des échelles fondamentalement différentes. Supposons, par exemple, que mon modèle de régression vise à prédire le quotient intellectuel des gens en utilisant leur niveau de scolarité (nombre d’années de scolarité) et leur revenu comme prédicteurs. De toute évidence, le niveau d’instruction et le revenu ne sont pas sur la même échelle. Le nombre d’années de scolarité ne peut varier que de 10 d’années, alors que le revenu peut varier de 10 000 dollars (ou plus). Les unités de mesure ont une grande influence sur les coefficients de régression. Les coefficients b n’ont de sens que lorsqu’ils sont interprétés à la lumière des unités, tant pour les prédicteurs que pour la variable résultat. Il est donc très difficile de comparer les coefficients des différents prédicteurs. Pourtant, il y a des situations où l’on souhaite vraiment faire des comparaisons entre différents coefficients. Plus précisément, vous pouvez vouloir une sorte de mesure standard pour déterminer quels prédicteurs ont la relation la plus forte avec la variable résultat. C’est ce que les coefficients standardisés visent à faire.

L’idée de base est assez simple ; les coefficients standardisés sont les coefficients que vous auriez obtenus si vous aviez converti toutes les variables en z-scores avant de calculer la régression¹⁰². L’idée ici est qu’en convertissant tous les prédicteurs en z-scores, ils entrent tous dans la régression sur la même échelle, ce qui élimine le problème d’avoir des variables sur différentes échelles. Quelle que soit la variable initiale, une valeur \(\beta\) de 1 signifie qu’une augmentation du prédicteur d’un écart-type produira une augmentation correspondante d’un écart-type sur la variable résultat. Par conséquent, si la variable A a une valeur absolue de \(\beta\) supérieure à celle de la variable B, on considère qu’elle a une relation plus forte avec le résultat. C’est l’idée du moins. Il faut cependant être un peu prudent ici, car cela repose en grande partie sur l’hypothèse selon laquelle « un changement d’écart type de 1 » est fondamentalement le même genre de chose pour toutes les variables. Il n’est pas toujours évident que ce soit vrai.

Si l’on laisse de côté les questions d’interprétation, examinons la façon dont elle est calculée. Ce que vous pourriez faire, c’est standardiser toutes les variables vous-même, puis effectuer une régression, mais il y a un moyen beaucoup plus simple de le faire. Il s’avère que le coefficient \(\beta\) pour un prédicteur X et un résultat Y a une formule très simple, à savoir

\[ \beta_{X} = b_{X} \times \frac{\sigma_{X}}{\sigma_{Y}} \]

où \(\sigma_{X}\) est l’écart-type du prédicteur et \(\sigma_{Y}\) est l’écart-type de la variable résultat Y. Cela rend les choses beaucoup plus simples.

Pour rendre les choses encore plus simples, Jamovi a une option qui calcule les coefficients de \(\beta\) pour vous en utilisant la case à cocher « Standardized estimate » dans les options « Model Coefficients », voir les résultats à la Figure 12‑16.

Ceci montre clairement que la variable dan.sleep a un effet beaucoup plus fort que la variable baby.sleep. Cependant, c’est l’exemple parfait d’une situation où il serait probablement plus judicieux d’utiliser les coefficients originaux b plutôt que les coefficients standardisés \(\beta\). Après tout, mon sommeil et le sommeil du bébé sont déjà sur la même échelle : le nombre d’heures de sommeil. Pourquoi compliquer les choses en les convertissant en z-scores ?

Figure 12‑16 : Coefficients normalisés avec des intervalles de confiance à 95 %, pour la régression linéaire multiple

12.9 Hypothèses de régression

Le modèle de régression linéaire dont j’ai parlé repose sur plusieurs hypothèses. Dans la Section 12.10, nous développerons la façon de vérifier ces hypothèses, mais examinons d’abord chacune d’entre elles.

• Normalité. Comme beaucoup de modèles statistiques, la régression linéaire simple ou multiple de base repose sur une hypothèse de normalité. Plus précisément, il suppose que les résidus sont normalement répartis. En fait, il n’y a pas de problème si les prédicteurs X et le résultat Y sont anormaux, pourvu que les résidus soient normaux. Voir section 12.10.3.

• Linéarité. Une hypothèse assez fondamentale du modèle de régression linéaire est que la relation entre X et Y est linéaire ! Qu’il s’agisse d’une régression simple ou d’une régression multiple, nous supposons que les relations impliquées sont linéaires.

• Homogénéité de la variance. Strictement parlant, le modèle de régression suppose que chaque résidu i est généré à partir d’une distribution normale avec une moyenne 0, et (ce qui est plus important pour les besoins actuels) avec un écart type identique pour chaque résidu. Dans la pratique, il est impossible de vérifier l’hypothèse selon laquelle chaque résidu est distribué de façon identique. Au lieu de cela, ce qui nous importe, c’est que l’écart-type du résidu soit le même pour toutes les valeurs de \(\hat{Y}\), et (si nous sommes particulièrement paranoïaques) toutes les valeurs de chaque prédicteur X dans le modèle.

• Prédicteurs non corrélés. L’idée ici est que, dans un modèle de régression multiple, vous ne voulez pas que vos prédicteurs soient trop fortement corrélés les uns aux autres. « Techniquement », ce n’est pas une hypothèse du modèle de régression, mais dans la pratique, c’est nécessaire. Des prédicteurs trop fortement corrélés les uns aux autres (ce qu’on appelle la « colinéarité ») peuvent poser des problèmes lors de l’évaluation du modèle. Voir la section 12.10.4.

• Les résidus sont indépendants les uns des autres. Il ne s’agit en fait que d’une hypothèse « passe-partout », avec la supposition que « il n’y a rien d’autre de bizarre dans les résidus ». S’il se passe quelque chose de bizarre (p. ex., les résidus dépendent tous fortement d’une autre variable non mesurée), cela pourrait tout gâcher.

Pas de valeurs aberrantes. Encore une fois, il ne s’agit pas en fait d’une hypothèse technique du modèle (ou plutôt d’une hypothèse implicite de tous les autres), mais il y a une hypothèse implicite que votre modèle de régression n’est pas trop fortement influencé par une ou deux données aberrantes qui pourraient remettre en cause la pertinence du modèle et la fiabilité des données dans certains cas. Voir section 12.10.2.

12.10 Vérification du modèle

L’objectif principal de cette section est la vérification du modèle de régression, un terme qui fait référence à l’art de vérifier que les hypothèses de votre modèle de régression ont été respectées, de trouver comment corriger le modèle si les hypothèses ne sont pas satisfaites, et généralement de vérifier qu’il n’y a rien de « bizarre ». C’est ce que j’appelle, à juste titre, « l’art » de la vérification des modèles. Ce n’est pas facile, et bien qu’il y ait beaucoup d’outils assez standardisés que vous puissiez utiliser pour diagnostiquer et peut-être même résoudre les problèmes qui affectent votre modèle (s’il y en a !), vous devez vraiment faire preuve d’un certain jugement en faisant cela. Il est facile de se perdre dans tous les détails de la vérification de telle ou telle caractéristique, et c’est assez épuisant d’essayer de se rappeler ces différentes composantes. Cela a pour effet secondaire très désagréable que beaucoup de gens sont frustrés lorsqu’ils essaient d’apprendre tous ces outils, ce qui les pousse à plutôt de ne pas faire de vérification du modèle. C’est un peu inquiétant !

Dans cette section, je décris plusieurs contrôles différents que vous pouvez faire pour vous assurer que votre modèle de régression fait ce qu’il est censé faire. Cela ne couvre pas tout ce que vous pourriez faire, mais c’est beaucoup plus détaillé que ce que je vois beaucoup de gens faire dans la pratique, et même moi je ne présente généralement pas tout cela dans mon cours d’introduction aux statistiques non plus. Toutefois, je pense qu’il est important que vous sachiez quels outils sont à votre disposition, alors je vais essayer d’en présenter quelques-uns ici. Enfin, je dois noter que cette section s’inspire beaucoup du texte de Fox et Weisberg (2011), le livre associé au package car qui est utilisé pour effectuer l’analyse de régression dans R. Le package car est réputé pour fournir d’excellents outils de diagnostic de régression, et le livre lui-même en parle d’une manière admirablement claire. Je ne veux pas paraître trop brusque, mais je pense que Fox et al (2011) vaut la peine d’être lu, même si certaines des techniques de diagnostic avancées ne sont disponibles que sous R et non dans Jamovi.

12.10.1 Trois types de résidus

La majorité des diagnostics de régression tournent autour de l’examen des résidus, et maintenant vous avez probablement forgé une théorie assez pessimiste des statistiques pour pouvoir deviner que, précisément parce que nous tenons beaucoup aux résidus, il existe en fait différentes catégories de résidus que nous pouvons considérer. En particulier, les trois types de résidus suivants sont mentionnés dans la présente section : les “résidus ordinaires”, les “résidus normalisés” et les “résidus studentisés”. Il y en a un quatrième type dont il est question dans certaines des figures, et c’est le résidu de Pearson. Toutefois, pour les modèles dont il est question dans ce chapitre, le résidu de Pearson est identique au résidu ordinaire.

Le premier et le plus simple des résidus dont nous nous soucions sont les résidus ordinaires. Ce sont les résidus bruts dont j’ai parlé tout au long de ce chapitre jusqu’à maintenant. La valeur résiduelle ordinaire est juste la différence entre la valeur ajustée \({\hat{Y}}_{i}\) et la valeur observée Y_i. J’ai utilisé l’indice i pour faire référence au i-ème résidu ordinaire, et je vais m’y tenir. En gardant à l’esprit que nous avons l’équation très simple suivante

\[ \epsilon_{i} = Y_{i} - {\hat{Y}}_{i} \]

C’est bien sûr ce que nous avons vu plus tôt, et à moins que je ne fasse spécifiquement référence à un autre type de résidu, c’est de celui-ci dont je parle. Il n’y a donc rien de nouveau ici. Je voulais juste me répéter. L’un des inconvénients de l’utilisation des résidus ordinaires est qu’ils sont toujours sur une échelle différente, selon la variable résultats et la qualité du modèle de régression. Autrement dit, à moins que vous n’ayez décidé d’exécuter un modèle de régression sans intersection, les résidus ordinaires auront une moyenne de 0, mais la variance est différente pour chaque résidus. Dans de nombreux contextes, en particulier lorsque l’on ne s’intéresse qu’à l’évolution des résidus et non à leurs valeurs réelles, il est commode d’estimer les résidus normalisés de manière à avoir un écart type 1.

La façon dont nous les calculons est de diviser le résidu ordinaire par une estimation de l’écart-type (de la population) de ces résidus. Pour des raisons techniques, la formule est la suivante

\[ \epsilon_{i}^{'} = \frac{\epsilon_{i}}{\hat{\sigma}\sqrt{1 - h_{i}}} \]

où \(\hat{\sigma}\) dans ce contexte est l’écart-type de population estimé des résidus ordinaires, et h_i est la « valeur chapeau » de la i-ième observation. Je ne vous ai pas encore expliqué ces valeurs (mais n’ayez crainte¹⁰³, ça va venir bientôt), donc ça n’aura pas beaucoup de sens. Pour l’instant, il suffit d’interpréter les résidus standardisés comme si nous avions converti les résidus ordinaires en z-scores. En fait, c’est plus ou moins la vérité, c’est juste que c’est un peu plus chic.

Le troisième type de résidus sont les résidus Studentisés (aussi appelés « résidus en portefeuille¹⁰⁴ ») et ils sont encore plus fantaisistes que les résidus standardisés. Encore une fois, l’idée est de prendre le résidu ordinaire et de le diviser par une certaine quantité afin d’estimer une notion standardisée du résidu.

La formule pour faire les calculs cette fois-ci est subtilement différente

\[ \epsilon_{i}^{*} = \frac{\epsilon_{i}}{{\hat{\sigma}}_{( - 1)}\sqrt{1 - h_{i}}} \]

Notez que notre estimation de l’écart-type ici est écrite \({\hat{\sigma}}_{( - 1)}\). Cela correspond à l’estimation de l’écart-type résiduel que vous auriez obtenu si vous veniez de supprimer la ième observation de l’ensemble de données. Cela ressemble à un cauchemar à calculer, puisque cela suggère qu’il faut exécuter N nouveaux modèles de régression (même un ordinateur moderne pourrait râler pour cela, surtout si vous avez un grand ensemble de données). Heureusement, une personne très intelligente a montré que cette estimation de l’écart-type est en fait donnée par l’équation suivante :

\[ \sigma_{( - 1)} = \hat{\sigma}\sqrt{\frac{N - K - 1 - \epsilon_{i}^{'2}}{N - K - 2}} \]

Ce n’est pas une pépite ?

Avant de poursuivre, je dois souligner que vous n’avez pas souvent besoin d’obtenir vous-même ces résidus, même s’ils sont au cœur de presque tous les diagnostics de régression. La plupart du temps, les différentes options qui fournissent les diagnostics, ou les vérifications des hypothèses, s’occuperont de ces calculs pour vous. Malgré tout, il est toujours agréable de savoir comment s’en emparer au cas où vous auriez besoin de faire quelque chose de non standard.

12.10.2 Trois types de données anormales

Un danger que vous pouvez rencontrer avec les modèles de régression linéaire est que votre analyse pourrait être disproportionnellement sensible à un petit nombre d’observations « inhabituelles » ou « anormales ». J’ai déjà discuté de cette idée à la section 5.2.3 dans le contexte des valeurs aberrantes qui sont automatiquement identifiées avec en traçant un boxplot sous « Exploration » -« Descriptives », mais cette fois nous devons être beaucoup plus précis. Dans le contexte de la régression linéaire, il y a trois façons conceptuellement distinctes d’envisager une observation « anormale ». Tous les trois sont intéressants, mais elles ont des implications assez différentes pour votre analyse.

Le premier type d’observation inhabituelle est une observation aberrante. La définition d’une valeur aberrante (dans ce contexte) est une observation très différente de ce que le modèle de régression prévoit. La Figure 12‑17 en donne un exemple. En pratique, nous opérationnalisons ce concept en disant qu’une valeur aberrante est une observation qui a un très grand résidu de studentisé, \(\epsilon_{i}\). Les valeurs aberrantes sont intéressantes : une valeur aberrante importante peut correspondre à des données inutiles, par exemple, les variables peuvent avoir été enregistrées incorrectement dans l’ensemble de données, ou un autre défaut peut être détectable. Notez que vous ne devriez pas jeter une observation simplement parce qu’il s’agit d’une observation aberrante. Mais le fait qu’il s’agisse d’une valeur aberrante indique souvent qu’il faut examiner ce cas de plus près et essayer de comprendre pourquoi il est si différent.

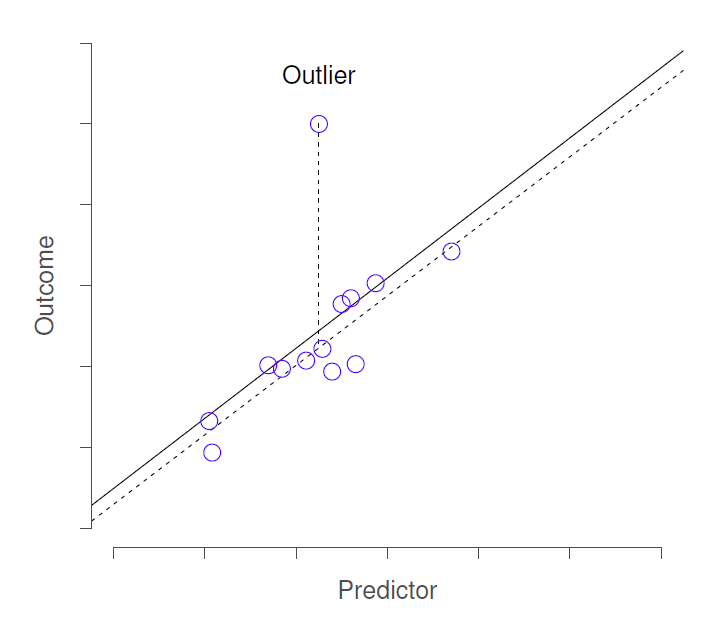
Figure 12‑17 : Une illustration des valeurs aberrantes. Les lignes pointillées représentent la ligne de régression qui aurait été estimée sans l’observation anormale incluse, et le résidu correspondant (c.-à-d. le résidu de studentisé). La ligne continue montre la ligne de régression avec l’observation anormale incluse. La valeur aberrante a une valeur inhabituelle sur la variable résultat (emplacement de l’axe des y), mais pas sur le prédicteur (emplacement de l’axe des x), et se trouve loin de la ligne de régression.

La deuxième façon pour une observation d’être inhabituelle est d’avoir un effet de levier élevé, ce qui se produit lorsque l’observation est très différente de toutes les autres observations. Cela ne doit pas nécessairement correspondre à un résidu important. Si l’observation se révèle inhabituelle exactement de la même façon pour toutes les variables, elle peut en fait se situer très près de la ligne de régression. La Figure 12‑18 en donne un exemple. L’effet de levier d’une observation est opérationnalisé par sa valeur chapeau, généralement écrite en hi. La formule de la valeur du chapeau est assez compliquée¹⁰⁵, mais son interprétation ne l’est pas : hi est une évaluation de « l’influence » de la i-ème observation sur l’orientation finale de la ligne de régression.

En général, si une observation est éloignée des autres en termes de variables prédictrices, elle aura une grande valeur chapeau (à titre indicatif, un effet de levier élevé est obtenu lorsque la valeur de chapeau est plus de 2-3 fois la moyenne ; notez également que la somme des valeurs chapeau est obligatoirement égale à K + 1).

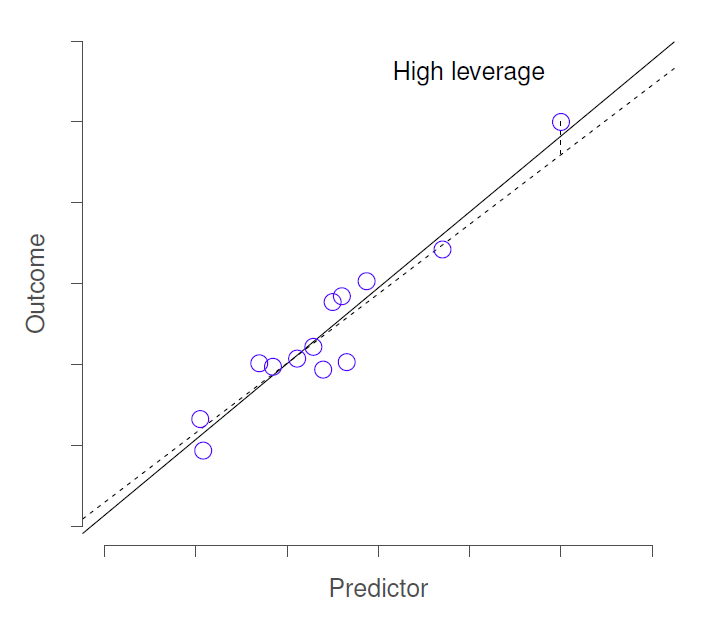
Figure 12‑18 : Illustration des points à fort effet de levier. L’observation anormale dans ce cas est inhabituelle, tant du point de vue du prédicteur (axe des x) que du résultat (axe des y), mais cette écart est très cohérent avec le modèle de corrélations qui existe entre les autres observations. L’observation est très proche de la ligne de régression et ne la déforme pas.

Les points à fort effet de levier valent également la peine d’être examinés plus en détail, mais ils sont beaucoup moins susceptibles d’être une source de préoccupation à moins qu’ils ne soient aussi des valeurs aberrantes.

Cela nous amène à notre troisième mesure de l’originalité, l’influence d’une observation. Une observation à forte influence est une valeur aberrante qui a un effet de levier élevé. C’est-à-dire qu’il s’agit d’une observation qui est très différente de toutes les autres à certains égards, et qui se situe aussi très loin de la ligne de régression. Ceci est illustré à la Figure 12‑19. Remarquez le contraste avec les deux types de valeurs précédents. Les valeurs aberrantes ne déplacent pas beaucoup la ligne de régression et les points de levier élevés non plus. Mais une donnée qui est à la fois une valeur aberrante et qui a un effet de levier élevé a un effet important sur la droite de régression. C’est pourquoi nous parlons pour ces points d’une grande influence, et c’est pourquoi ils nous préoccupent plus. Nous opérationnalisons l’influence en fonction d’une mesure appelée distance de Cook.

\[ D_{i} = \frac{\epsilon_{i}^{*2}}{K + 1} \times \frac{h_{i}}{1 - h_{1}} \]

Notez qu’il s’agit d’une multiplication d’une mesure de la valeur aberrante de l’observation (la partie à gauche), d’une mesure de l’effet de levier de l’observation (la partie à droite).

Afin d’avoir une grande distance de Cook, une observation doit être une valeur aberrante assez importante et avoir un effet de levier élevé. A titre indicatif, la distance de Cook supérieure à 1 est souvent considérée comme grande (c’est ce que j’utilise généralement comme une règle rapide et approximative).

Dans Jamovi, l’information sur la distance du Cook peut être calculée en cliquant sur la case à cocher « Cook’s Distance » dans les options « Assumption Checks » - « Data Summary ». Dans le cas du modèle de régression multiple que nous avons utilisé comme exemple dans ce chapitre, vous obtenez les résultats présentés à la Figure 12‑20.

Vous pouvez voir que, dans cet exemple, la valeur moyenne de la distance de Cook est de 0,01, et la plage est de 0,0000000262 à 0,11, donc c’est un peu loin de la règle empirique mentionnée ci-dessus une distance de Cook supérieure à 1 est considérée comme grande.

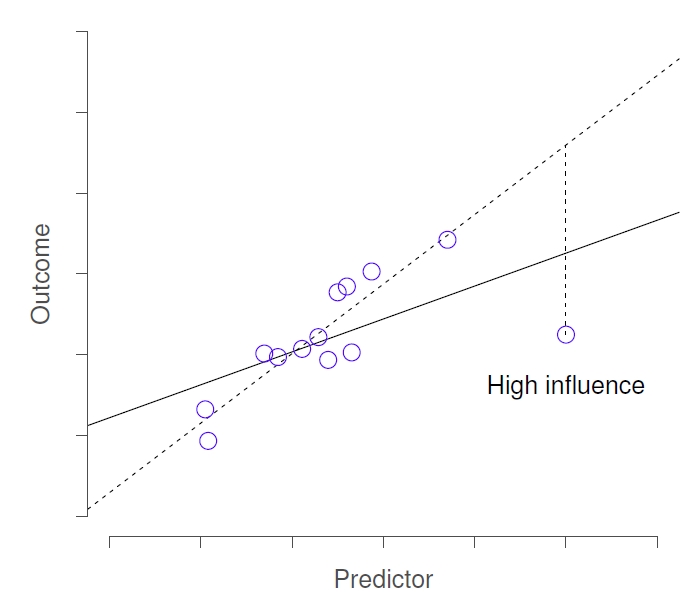
Figure 12‑19 : Illustration des points d’influence élevés. Dans ce cas, l’observation anormale est très inhabituelle sur la variable prédictive (axe des x) et se situe très loin de la ligne de régression. Par conséquent, la ligne de régression est fortement déformée, même si (dans ce cas) l’observation anormale est tout à fait typique en termes de variable résultat (axe des y).

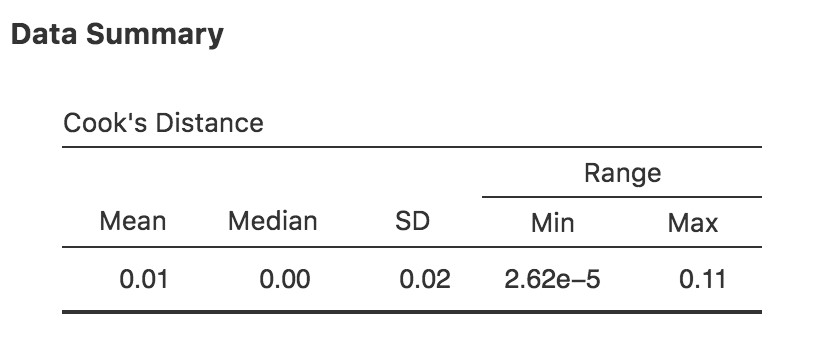
Figure 12‑20 : Copie d’écran Jamovi montrant le tableau pour les statistiques de la distance du Cook

Une question évidente à se poser ensuite est la suivante : si vous avez de grandes valeurs pour la distance de Cook, que devez-vous faire ? Comme toujours, il n’y a pas de règle absolue. La première chose à faire est probablement d’essayer d’exécuter la régression avec la valeur aberrante dont la plus grande distance de Cook est exclue¹⁰⁶ et de voir ce qui arrive au modèle et aux coefficients de régression. S’ils sont vraiment très différents, il est temps de commencer à fouiller dans votre ensemble de données et les notes que vous que vous avez sans aucun doute gribouillées lorsque vous avez mené votre étude. Essayez de comprendre pourquoi c’est si différent. Si cela vous conduit à penser que cette données fausse gravement vos résultats, vous pouvez envisager de l’exclure, mais c’est loin d’être idéal, à moins que vous n’ayez une explication solide sur le fait que ce cas particulier est qualitativement différent des autres et mérite donc d’être traité séparément.

12.10.3 Vérification de la normalité des résidus

Comme bon nombre des outils statistiques dont nous avons discuté dans ce livre, les modèles de régression reposent sur une hypothèse de normalité. Dans ce cas, nous supposons que les résidus sont normalement répartis. La première chose que nous pouvons faire est de tracer un graphique QQ via l’option « Assumption Checks » - « Q-Q plot of residuals ».

La sortie est illustrée à la Figure 12‑21, montrant les résidus standardisés représentés sur le graphique en fonction de leurs quantiles théoriques selon le modèle de régression.

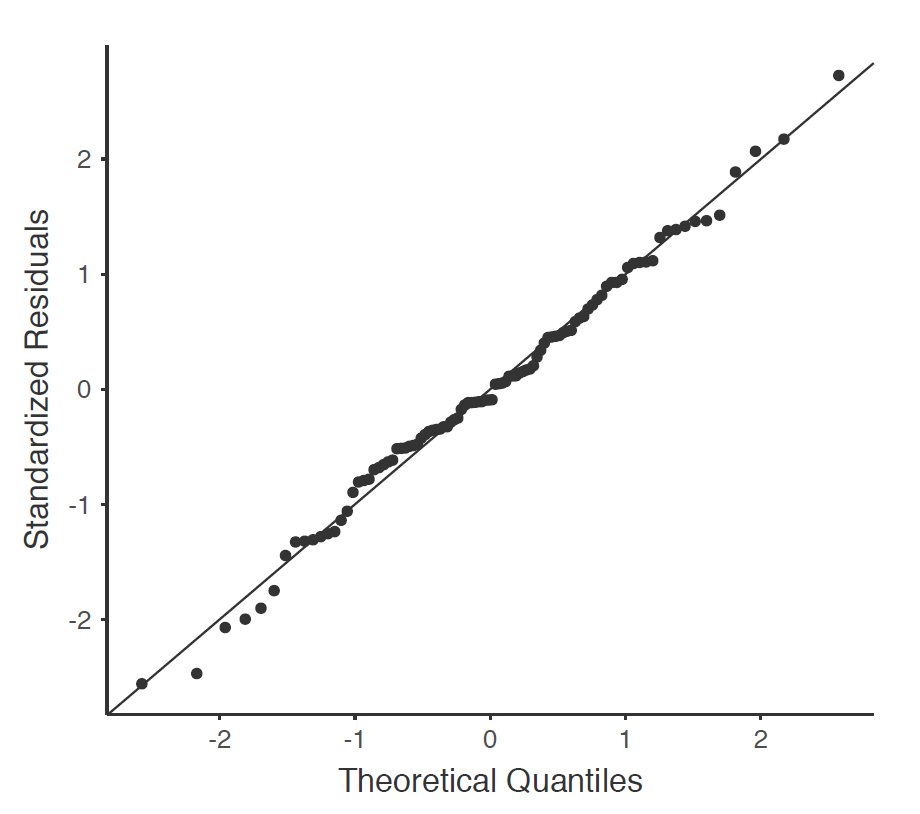
Figure 12‑21 : Représentation graphique des quantiles théoriques suivant le modèle, par rapport aux quantiles des résidus normalisés, produits avec Jamovi

Nous devrions vérifier également la relation entre les valeurs ajustées et les résidus eux-mêmes. Pour ce faire, Jamovi peut utiliser l’option « Residuals Plots », qui fournit un diagramme de dispersion pour chaque variable prédictive, entre la variable résultat et les valeurs ajustées par rapport aux résidus, voir la Figure 12‑22. Dans ces figures, nous recherchons une distribution assez uniforme des « points » sans regroupement ni structuration claire. Si l’on regarde ces figures, il n’y a rien de particulièrement inquiétant puisque les points sont répartis de façon assez uniforme sur l’ensemble de la figure. Il peut y avoir un peu de non-uniformité dans le graphique (b), mais ce n’est pas un écart important et il ne vaut probablement pas la peine de s’en inquiéter.

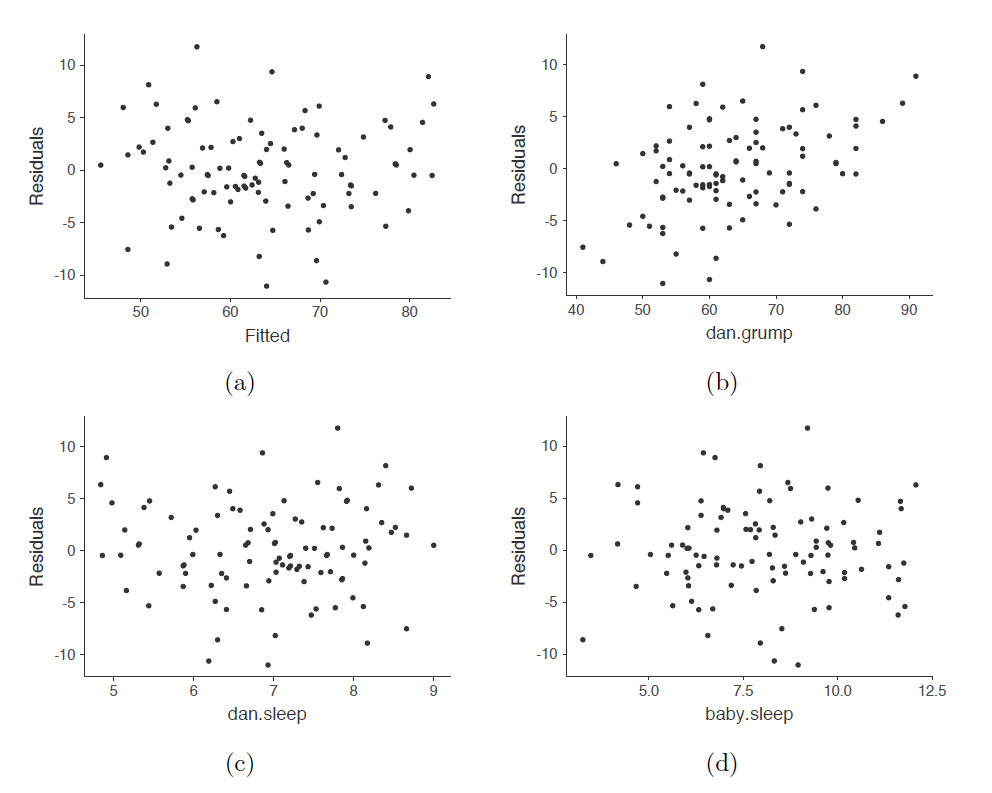
Figure 12‑22 : Graphique des résidus réalisés avec Jamovi

Si nous étions inquiets, la solution à ce problème (et à bien d’autres encore) consiste dans bien des cas à transformer une ou plusieurs variables. Nous avons discuté des bases de la transformation des variables dans les sections 6.3 et 6.4, mais je tiens à souligner une autre possibilité que je n’ai pas expliquée en détail plus tôt : la transformation Box-Cox. La fonction Box-Cox est assez simple et elle est très largement utilisée

\[ f\left( x,\lambda \right) = \frac{x^{\lambda} - 1}{\lambda} \]

pour toutes les valeurs de \(\lambda\) sauf \(\lambda=0\). Quand \(\lambda=0\) nous prenons juste le logarithme naturel (i.e. ln(x)). Vous pouvez le calculer à l’aide de la fonction BOXCOX de l’écran « Compute » des feuilles de données dans Jamovi.

12.10.4 Vérification de la colinéarité

Le dernier type de diagnostic de régression que je vais aborder dans ce chapitre est l’utilisation des facteurs d’inflation de variance (VIF), qui sont utiles pour déterminer si les prédicteurs de votre modèle de régression sont trop fortement corrélés les uns aux autres. Il y a un facteur d’inflation de variance associé à chaque prédicteur X_k du modèle.

La formule pour le k-ème VIF est :

\[ \text{VIF}_{k} = \frac{1}{1 - R_{( - k)}^{2}} \]

Où \(R_{( - k)}^{2}\) renvoie à la valeur R-carrée que vous obtiendriez si vous exécutiez une régression en utilisant X_k comme variable de résultat, et toutes les autres variables X comme prédicteurs. L’idée ici est que \(R_{( - k)}^{2}\) est une très bonne mesure de la mesure de la corrélation enre X_k et toutes les autres variables du modèle.

La racine carrée de VIF est aisément interprétable. Elle est une mesure du fait que l’intervalle de confiance pour le coefficient b_k correspondant est plus grand que ce à quoi vous vous attendriez si les variables prédictrices étaient toutes indépendantes et non corrélées les unes aux autres. Si vous n’avez que deux prédicteurs, les valeurs VIF seront toujours les mêmes, comme nous pouvons le voir en cochant « Collinearity » dans les options « Regression » - « Assumptions » dans Jamovi. Pour dan.sleep et baby.sleep, la VIF est de 1,65. Et puisque la racine carrée de 1,65 est de 1,28, nous constatons que la corrélation entre nos deux prédicteurs ne pose pas de problème.

Pour donner une idée de ce que nous pourrions nous trouver avec un modèle qui pose des problèmes de colinéarité plus importants, supposons que j’exécute un modèle de régression beaucoup moins intéressant, dans lequel j’essaie de prédire le jour où les données sont recueillies, en fonction de toutes les autres variables de l’ensemble des données. Pour comprendre pourquoi ce serait un peu problématique, jetons un coup d’oeil à la matrice de corrélation des quatre variables :

Nous avons des corrélations assez importantes entre certaines de nos variables prédictrices ! Lorsque nous exécutons le modèle de régression et que nous examinons les valeurs de VIF, nous constatons que la colinéarité cause beaucoup d’incertitude pour les coefficients. Si vous exécutez la régression, comme dans la Figure 12‑23 alors vous pouvez voir d’après les valeurs de VIF que c’est là une très bonne colinéarité.

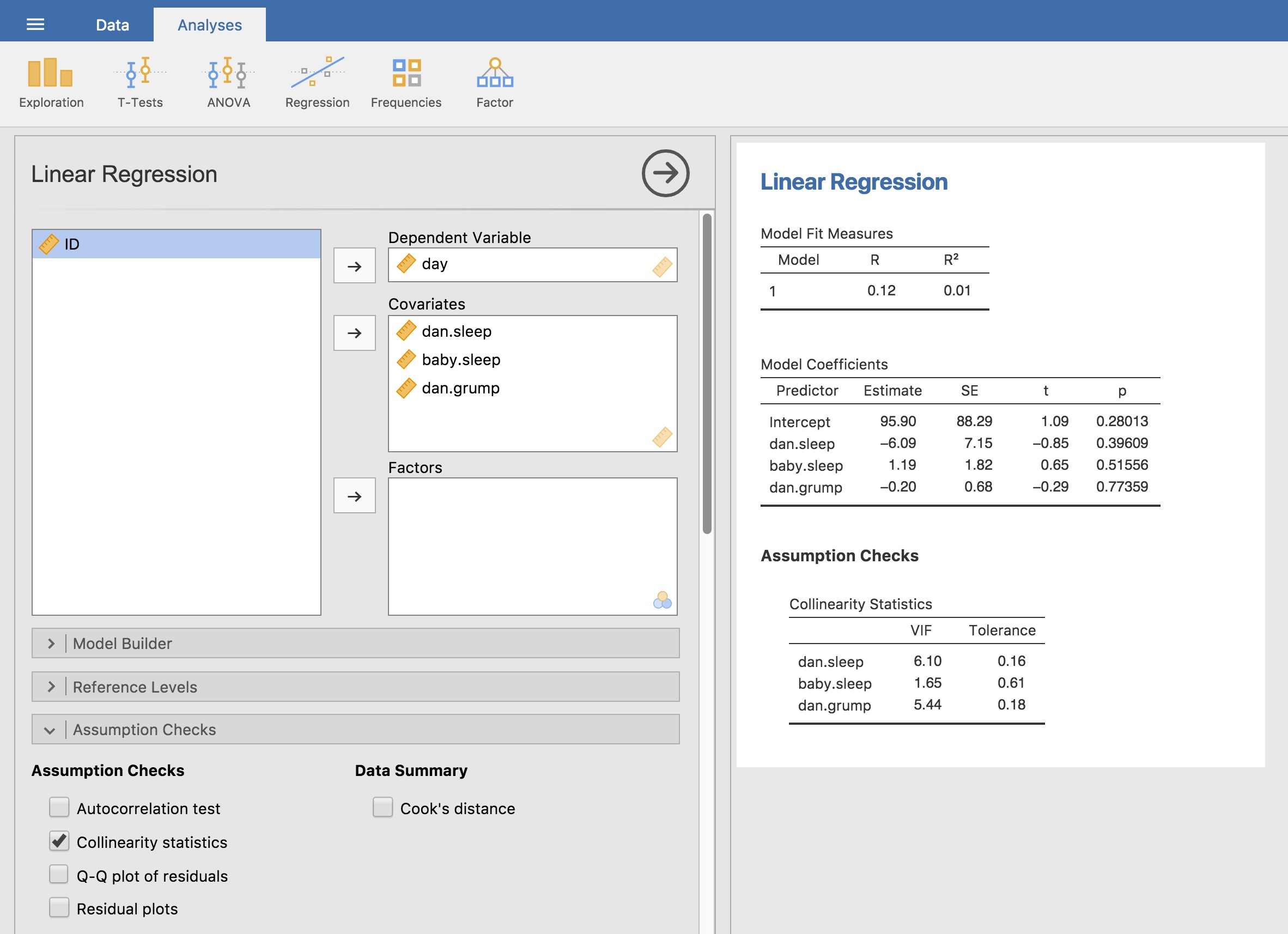
Figure 12‑23 : Statistiques de colinéarité pour la régression multiple produites avec Jamovi

12.11 Choix du modèle

Un problème assez important subsiste, celui de la « sélection des modèles ». Autrement dit, si nous avons un ensemble de données qui contient plusieurs variables, lesquelles devrions-nous inclure comme prédicteurs et lesquelles ne devrions-nous pas inclure ? Dit autrement, nous avons un problème de sélection de variables. En général, la sélection d’un modèle est une affaire complexe, mais elle est quelque peu simplifiée si nous nous limitons au problème du choix d’un sous-ensemble des variables qui devraient être incluses dans le modèle. Néanmoins, je ne vais pas essayer de couvrir ce sujet, même réduit, très en détails. Au lieu de cela, je vais parler de deux grands principes auxquels vous devez réfléchir, puis discuter d’un outil concret que Jamovi fournit pour vous aider à sélectionner un sous-ensemble de variables à inclure dans votre modèle. Premièrement, les deux principes :

• C’est bien d’avoir une base substantielle pour vos choix. En d’autres termes, dans bien des situations, le chercheur a de bonnes raisons de choisir un petit nombre de modèles de régression possibles qui présentent un intérêt théorique. Ces modèles auront une interprétation ayant du sens dans le contexte de votre domaine. Ne négligez jamais l’importance de cette question. Les statistiques servent le processus scientifique, et non l’inverse.

• Dans la mesure où vos choix reposent sur l’inférence statistique, il y a un compromis entre la simplicité et la qualité de l’ajustement. Plus vous ajoutez de variables prédictrices au modèle, plus il devient complexe. Chaque prédicteur ajoute un nouveau paramètre libre (c.-à-d. un nouveau coefficient de régression) et chaque nouveau paramètre augmente la capacité du modèle à « absorber » les variations aléatoires. Ainsi, la qualité de l’ajustement (p. ex., R2) continue d’augmenter, parfois de façon triviale ou par hasard, à mesure que vous ajoutez d’autres variables prédicteurs quoi qu’il arrive. Si vous voulez que votre modèle soit capable de bien généraliser à de nouvelles observations, vous devez éviter d’ajouter trop de variables.

Ce dernier principe est souvent appelé le rasoir d’Ockham et est souvent résumé par le dicton succinct suivant : ne pas multiplier les entités au-delà de la nécessité. Dans ce contexte, cela signifie qu’il ne faut pas balancer un tas de prédicteurs largement non pertinents juste pour augmenter votre R². Oui, l’original était mieux.

Quoi qu’il en soit, ce dont nous avons besoin, c’est d’un critère mathématique concret qui appliquera le principe qualitatif du rasoir d’Ockham dans le contexte du choix d’un modèle de régression. Il s’avère qu’il y a plusieurs possibilités. Celui dont je vais parler est le critère d’information Akaike (AIC ; Akaike, (1974)) simplement parce qu’il est disponible en option dans Jamovi.

Dans le contexte d’un modèle de régression linéaire (et en ignorant les termes qui ne dépendent d’aucune façon du modèle !), l’AIC pour un modèle qui a K variables prédicteurs plus une intersection est

\[ AIC = \frac{\text{SS}_{\text{res}}}{{\hat{\sigma}}^{2}} + 2K \]

Plus la valeur AIC est faible, meilleures sont les performances du modèle. Si nous ignorons les détails de bas niveau, ce que fait l’AIC est assez évident. À gauche, nous avons un terme qui augmente à mesure que les prédictions du modèle empirent ; à droite, nous avons un terme qui augmente à mesure que la complexité du modèle augmente. Le meilleur modèle est celui qui correspond bien aux données (faibles résidus, côté gauche) en utilisant le moins de prédicteurs possible (faible K, côté droit). En bref, il s’agit d’une simple mise en oeuvre du rasoir d’Ockham.

L’AIC peut être ajouté à la table de sortie « Model Fit Measures » avec la case à cocher « AIC », et une façon assez fastidieuse d’évaluer différents modèles consiste à voir si la valeur « AIC » est inférieure si l’on supprime un ou plusieurs des prédicteurs du modèle de régression. C’est la seule façon actuellement mise en oeuvre dans Jamovi, mais il existe des alternatives dans d’autres programmes plus puissants, tels que R. Ces méthodes alternatives peuvent automatiser le processus de suppression sélective (ou d’ajout) de variables prédictrices pour trouver le meilleur AIC. Bien que ces méthodes ne soient pas implémentées dans Jamovi, je vais les mentionner brièvement ci-dessous pour que vous les connaissiez.

12.11.1 Élimination rétrograde

Dans l’élimination rétrograde, vous commencez par le modèle de régression complet avec tous les prédicteurs possibles. Ensuite, à chaque « étape », nous essayons toutes les façons possibles d’éliminer l’une des variables, et celle qui est la meilleure (c.-à-d. ayant la valeur AIC la plus faible) est acceptée. Ceci devient notre nouveau modèle de régression, et nous essayons alors toutes les suppressions possibles dans le nouveau modèle, en choisissant à nouveau l’option avec l’AIC le plus bas. Ce processus se poursuit jusqu’à ce que nous obtenions un modèle dont la valeur AIC est inférieure à celle de tous les autres modèles possibles que vous pourriez produire en supprimant un de ses prédicteurs.

12.11.2 Sélection en avant

A la place, vous pouvez également essayer la sélectionner en avant. Cette fois-ci, nous partons du modèle le plus petit possible comme point de départ, et nous ne considérons que les ajouts possibles au modèle. Cependant, il y a une complication. Vous devez également préciser quel est le plus grand modèle possible que vous êtes prêt à accepter. Bien que la sélection rétroactive et en avant puisse mener à la même conclusion, ce n’est pas toujours le cas.

12.11.3 Une mise en garde

Les méthodes automatisées de sélection de variables sont séduisantes, surtout lorsqu’elles sont regroupées dans des fonctions (assez) simples de programmes statistiques puissants. Elles fournissent un élément d’objectivité à votre sélection de modèle, et c’est plutôt sympa. Malheureusement, ils servent parfois d’excuse à l’insouciance. Il n’est plus nécessaire de réfléchir soigneusement aux prédicteurs à ajouter au modèle et aux fondements théoriques de leur inclusion. Tout est résolu par la magie de l’AIC. Et si nous commençons à lancer des principes comme le rasoir d’Ockham, on dirait que tout est emballé dans un joli petit paquet que personne ne peut contester.

Ou, peut-être pas. Tout d’abord, il y a très peu d’accord sur ce qui est considéré comme un critère approprié de sélection de modèle. Lorsqu’on m’a enseigné l’élimination rétrograde durant le premier cycle, nous avons utilisé des tests F pour le faire, parce que c’était la méthode par défaut utilisée par le logiciel. J’ai décrit l’utilisation de l’AIC, et puisqu’il s’agit d’un texte d’introduction, c’est la seule méthode que j’ai décrite, mais l’AIC n’est guère la Parole des Dieux de la Statistique. Il s’agit d’une approximation, dérivée de certaines hypothèses, et il est garanti qu’elle ne fonctionne que pour de grands échantillons lorsque ces hypothèses sont respectées. Modifiez ces hypothèses et vous obtenez un critère différent, comme le BIC par exemple (également disponible en Jamovi). Adoptez à nouveau une approche différente et vous obtenez le critère NML. Décidez que vous êtes un Bayésien et vous obtenez une sélection de modèle basée sur les odds ratio à portériori. Il y a également un tas d’outils spécifiques à la régression que je n’ai pas mentionnés. Et ainsi de suite. Toutes ces différentes méthodes ont leurs forces et leurs faiblesses, et certaines sont plus faciles à calculer que d’autres (l’AIC est probablement la plus facile du lot, ce qui pourrait expliquer sa popularité). Presque toutes produisent les mêmes réponses lorsque la réponse est « évidente », mais il y a un certain nombre de désaccords lorsque le problème de sélection du modèle devient difficile.

Qu’est-ce que cela signifie en pratique ? Eh bien, je pourrais passer plusieurs années à vous enseigner la théorie de la sélection des modèles, en vous apprenant tous les tenants et aboutissants de celle-ci afin que vous puissiez enfin décider ce qui selon vous est la bonne méthode. En tant que personne qui a vraiment fait cela, je ne le recommanderais pas. Vous sortirez probablement encore plus confus que lorsque vous avez commencé. Une meilleure stratégie consiste à faire preuve d’un peu de bon sens. Si vous regardez les résultats d’une procédure de sélection automatisée en avant ou rétrograde, et que le modèle qui a du sens est proche d’avoir le plus petit AIC, mais est battu de justesse par un modèle qui n’a aucun sens, alors faites confiance à votre instinct. Le choix d’un modèle statistique est un outil inexact et, comme je l’ai dit au début, l’interprétabilité est importante.

12.11.4 Comparaison de deux modèles de régression

Une solution de rechange à l’utilisation de procédures automatisées de sélection de modèles consiste pour le chercheur à sélectionner explicitement deux ou plusieurs modèles de régression à comparer entre eux. Vous pouvez le faire de différentes façons, en fonction de la question de recherche à laquelle vous essayez de répondre. Supposons que nous voulions savoir si la durée de sommeil de mon fils a un rapport avec ma mauvaise humeur, au-delà de ce à quoi nous pourrions nous attendre pour la durée de mon sommeil. Nous voulons également nous assurer que le jour où la mesure est prise n’influence pas la relation. C’est-à-dire que nous nous intéressons à la relation entre baby.sleep et dan.grump, et de ce point de vue, dan.sleep et day sont des variables parasites ou covariables que nous voulons contrôler. Dans cette situation, nous aimerions savoir si dan.grump ~ dan.sleep + day + baby.sleep (que j’appellerai modèle 2, ou M2) est un meilleur modèle de régression pour ces données que dan.grump ~ dan.sleep + day (que je vais appeler modèle 1, ou M1). Il y a deux façons de comparer ces deux modèles, l’une basée sur un critère de sélection de modèle comme l’AIC, et l’autre basée sur un test d’hypothèse explicite. Je vais d’abord vous montrer l’approche fondée sur l’AIC parce qu’elle est plus simple et qu’elle découle naturellement de la discussion de la dernière section. La première chose que je dois faire est d’exécuter les deux régressions, de noter l’AIC pour chacune d’elles, puis de sélectionner le modèle avec la valeur AIC la plus petite, car on estime qu’il s’agit du meilleur modèle pour ces données. En fait, ne le faites pas tout de suite. Lisez la suite parce qu’il y a un moyen facile dans Jamovi d’obtenir les valeurs AIC pour différents modèles inclus dans un seul tableau.¹⁰⁷

Une approche quelque peu différente du problème découle du cadre de vérification des hypothèses. Supposons que vous ayez deux modèles de régression, dont l’un (modèle 1) contient un sous-ensemble des prédicteurs de l’autre (modèle 2). C’est-à-dire que le modèle 2 contient tous les prédicteurs inclus dans le modèle 1, plus un ou plusieurs prédicteurs supplémentaires. Lorsque cela se produit, nous disons que le modèle 1 est imbriqué dans le modèle 2, ou peut-être que le modèle 1 est un sous-modèle du modèle 2. Indépendamment de la terminologie, cela signifie que nous pouvons considérer le modèle 1 comme une hypothèse nulle et le modèle 2 comme une hypothèse alternative. Et en fait, nous pouvons construire un test F pour cela d’une manière assez simple.

Nous pouvons ajuster les deux modèles aux données et obtenir une somme résiduelle de carrés pour les deux modèles. Je les désignerai respectivement par \(\text{SS}_{\text{res}}^{(1)}\) et \(\text{SS}_{\text{res}}^{(2)}\). L’exposant ici indique simplement de quel modèle il s’agit. Alors notre statistique F est la suivante

\[ F = \frac{\text{SS}_{\text{res}}^{(1)} - \text{SS}_{\text{res}}^{(1)}/k}{\left( \text{SS}_{\text{res}}^{(2)} \right)/(N - p - 1)} \]

où N est le nombre d’observations, p est le nombre de prédicteurs dans le modèle complet (à l’exclusion de l’intersection) et k est la différence dans le nombre de paramètres entre les deux modèles¹⁰⁸.Les degrés de liberté sont ici k et N-p-1. Notez qu’il est souvent plus pratique de considérer la différence entre ces deux valeurs SS comme une somme de carrés à part entière. C’est-à-dire

\[ \text{SS}_{\Delta}=\text{SS}^{(1)}_{\text{res}}-\text{SS}^{(2)}_{\text{res}} \] C’est utile parce que nous pouvons exprimer \(\text{SS}_{\Delta}\) comme une évaluation de la mesure dans laquelle les deux modèles font des prédictions différentes au sujet de la variable des résultats.

\[ \text{SS}_{\Delta} = \sum_{i}^{}\left( {\hat{y}}_{\text{res}}^{(2)} - {\hat{y}}_{\text{res}}^{(1)} \right)^{2} \] Spécifiquement, quand \({\hat{y}}_{\text{res}}^{(1)}\) est la valeur ajustée pour yi selon le modèle M₁ et \({\hat{y}}_{\text{res}}^{(2)}\) est la valeur ajustée pour y_i selon le modèle M₂.

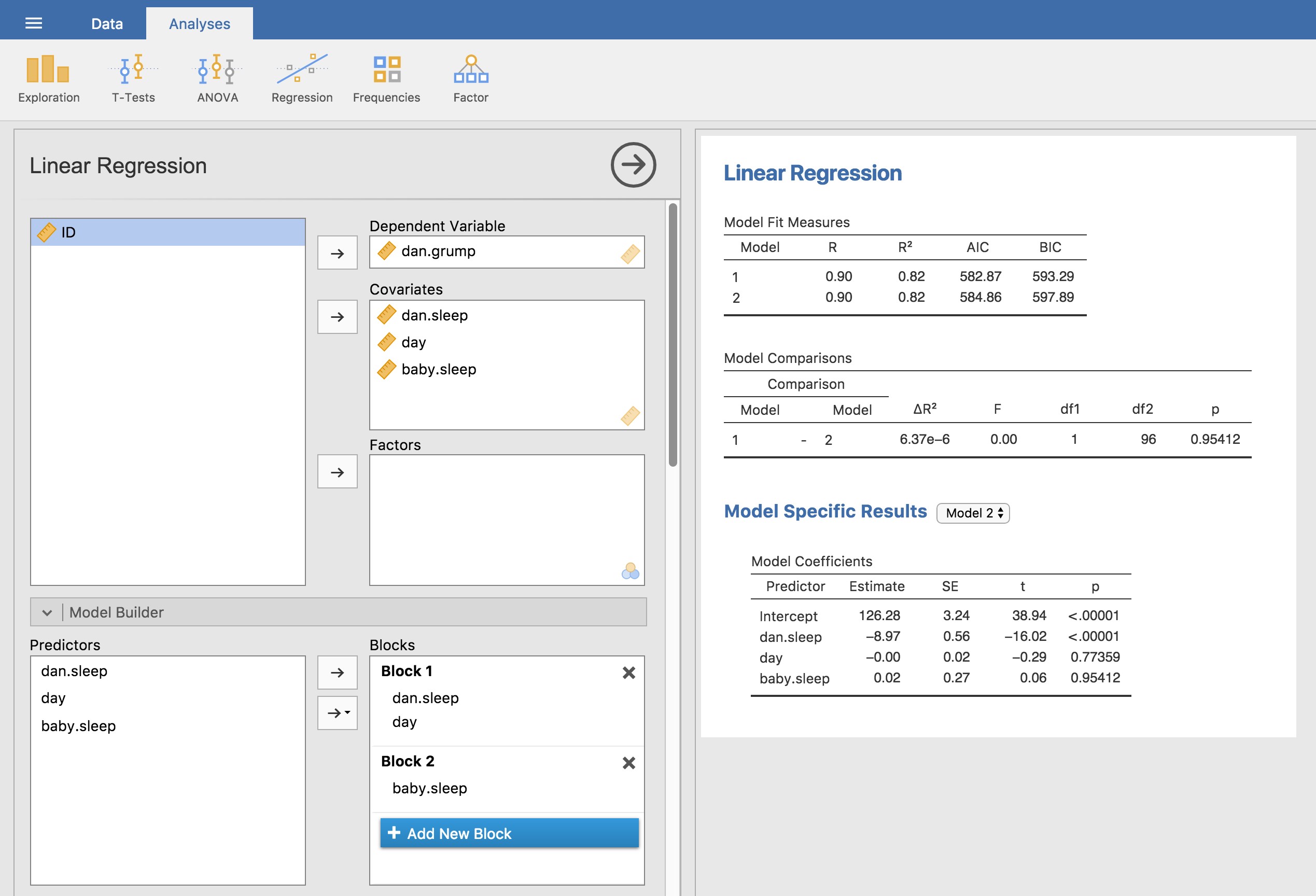
Figure 12‑24 : Comparaison de modèles dans Jamovi avec l’option « Model Builder »

C’est donc le test d’hypothèse que nous utilisons pour comparer deux modèles de régression. Maintenant, comment on fait ça à Jamovi ? La solution consiste à utiliser l’option « Model Builder » et de spécifier les prédicteurs du modèle 1 dan.sleep et day dans « Block 1 » puis d’ajouter le prédicteur supplémentaire du modèle 2 (baby.sleep) dans « Block 2 », comme dans la Figure 12‑24. Cela montre, dans le tableau « Model Comparisons », que pour les comparaisons entre le modèle 1 et le modèle 2, F_(1,96)=0,00, p=,954. Puisque nous avons p>.05, nous retenons l’hypothèse nulle (M₁). Cette approche de régression, dans laquelle nous additionnons toutes nos covariables dans un modèle nul, puis nous ajoutons les variables d’intérêt dans un modèle alternatif, puis nous comparons les deux modèles dans un cadre de vérification des hypothèses, est souvent appelée régression hiérarchique.

Nous pouvons également utiliser cette option « Model Comparison » pour afficher un tableau qui montre l’AIC et le BIC pour chaque modèle, ce qui facilite la comparaison et l’identification du modèle ayant la valeur la plus faible, comme dans la Figure 12‑24.

12.12 Résumé

• Vous voulez savoir à quel point la relation est forte entre deux variables ? Calculer une corrélation (section 12.1).

• Dessiner des diagrammes de dispersion (Section 12.2).

• Les idées de base de la régression linéaire et la façon dont les modèles de régression sont estimés (sections 12.3 et 12.4).

• Régression linéaire multiple (section 12.5).

• Mesure du rendement global d’un modèle de régression à l’aide de R2 (section 12.6).

• Tests d’hypothèse pour les modèles de régression (Section 12.7)

• Calcul des intervalles de confiance pour les coefficients de régression et les coefficients standardisés (section 12.8).

• Les hypothèses de régression (section 12.9) et comment les vérifier (section 12.10).

• Sélection d’un modèle de régression (Section 12.11).

References

Akaike, H. 1974. “A New Look at the Statistical Model Identification.” IEEE Transactions on Automatic Control 19 (6): 716–23. https://doi.org/10.1109/TAC.1974.1100705.

Anscombe, F. J. 1973. “Graphs in Statistical Analysis.” The American Statistician 27 (1): 17–21. https://doi.org/10.1080/00031305.1973.10478966.

Fox, John, and Sanford Weisberg. 2011. An R Companion to Applied Regression. 2nd Revised edition. Thousand Oaks, Calif: SAGE Publications, Inc.

---

92. J’ai remarqué que dans certaines versions de Jamovi vous pouvez aussi spécifier un type de variable’ID’, mais pour nos besoins, peu importe comment nous spécifions la variable ID car nous ne l’inclurons dans aucune analyse.↩︎

93. En fait, même cette table, c’est plus que ce que j’aurais voulu. Dans la pratique, la plupart des gens choisissent une mesure de la tendance centrale et une mesure de la variabilité seulement.↩︎

94. Tout comme nous l’avons vu avec la variance et l’écart-type, en pratique nous divisons par N-1 au lieu de N↩︎

95. C’est une simplification exagérée, mais ça fera l’affaire pour nous.↩︎

96. Également parfois écrit comme y = mx + c où m est le coefficient de pente et c est le coefficient d’intersection (constante).↩︎

97. NdT C’est ce qu’on appelle ordonnée à l’origine en géométrie. Pour faire court ce point sera désigné, comme l’on fait les auteurs par intersction dans le reste de l’ouvrage.↩︎

98. Ou du moins, je suppose que ça n’aide pas la plupart des gens. Mais au cas où quelqu’un lisant ceci est un véritable maître de kung-fu de l’algèbre linéaire (et pour être juste, j’ai toujours quelques-uns de ces gens dans ma classe d’introduction aux stats), cela vous aidera à savoir que la solution au problème d’estimation se révèle être \(\hat{b} = \left( X'X \right)^{- 1}X'y\),où \(\hat{b}\) est un vecteur contenant les coefficients estimés, X est la « matrice du plan » qui contient les variables de prévision (plus une colonne supplémentaire contenant toutes celles ; strictement X est une matrice des variables explicatives, mais je n’ai pas encore discuté de la distinction), et y est un vecteur contenant la variable résultat. Pour tout le monde, ce n’est pas vraiment utile et peut être carrément effrayant. Cependant, puisque beaucoup de choses en régression linéaire peuvent être écrites en termes d’algèbre linéaire, vous verrez un tas de notes de bas de page comme celle-ci dans ce chapitre. Si vous pouvez suivre ces maths, c’est génial. Si ce n’est pas le cas, ignorez-les.↩︎

99. Et par « parfois » je veux dire « presque jamais ». Dans la pratique, tout le monde l’appelle simplement « R-carré ».↩︎

100. Pour les lecteurs avancés seulement. Le vecteur des résidus est \(\epsilon = y - X\hat{b}\). Pour K prédicteurs plus l’intersection, la variance résiduelle estimée est \({\hat{\sigma}}^{2} = \epsilon^{'}\epsilon/(N - K - 1)\). La matrice de covariance estimée des coefficients est \({\hat{\sigma}}^{2}\left( X'X \right)^{- 1}\), dont la diagonale principale est \(\text{SE}\left( \hat{b} \right)\), notre erreur type estimée.↩︎

101. Notez que, bien que Jamovi a fait plusieurs tests ici, il n’a pas fait de correction de Bonferroni ou autre. Il s’agit de tests t standard à un échantillon avec une alternative bilatérale. Si vous voulez faire des corrections pour plusieurs tests, vous devez le faire vous-même.↩︎

102. Strictement, vous normalisez tous les variables explicatives. C’est-à-dire, chaque “chose” à laquelle est associé un coefficient de régression dans le modèle. Pour les modèles de régression dont j’ai parlé jusqu’à présent, chaque variable prédictive est représentée sur un seul régresseur, et vice versa. Cependant, ce n’est pas vraiment vrai en général et nous en verrons quelques exemples au chapitre 14. Mais, pour l’instant, nous n’avons pas besoin de trop nous soucier de cette distinction.↩︎

103. Ou ne l’esperez pas, selon le cas.↩︎

104. Ndt : Je conserve une traduction littérale, mais j’avoue n’avoir jamais rencontré cette appelation.↩︎

105. Encore une fois, pour les fanatiques de l’algèbre linéaire : la “matrice chapeau” est définie comme étant la matrice H qui convertit le vecteur des valeurs observées y en un vecteur des valeurs ajustées \(\hat{y}\), tel que \(\hat{y}=H_{y}\). Le nom vient du fait que c’est la matrice qui « met un chapeau sur y ». La valeur chapeau de la i-ème observation est le i-ème élément diagonal de cette matrice (donc techniquement je devrais l’écrire comme h_ii plutôt que h_i). Et au cas où ça vous intéresserait, voici comment ça se calcule : \(H = X(X’X)^{-1}X’\). N’est-ce pas joli ?↩︎

106. Parce qu’il n’y a actuellement pas de moyen très facile de le faire avec Jamovi, un programme de régression plus puissant tel que le package car de R serait préférable pour cette analyse plus avancée.↩︎

107. Tant que j’y suis, je dois souligner que les données empiriques suggèrent que le BIC est un meilleur critère que l’AIC. Dans la plupart des études de simulation que j’ai vues, le BIC sélectionne beaucoup mieux le bon modèle.↩︎

108. Il convient de noter au passage que cette même statistique F peut être utilisée pour tester un éventail beaucoup plus large d’hypothèses que celles que je mentionne ici. Très brièvement, notons que le modèle imbriqué M1 correspond au modèle complet M2 lorsque l’on contraint certains des coefficients de régression à zéro. Il est parfois utile de construire des sous-modèles en plaçant d’autres types de contraintes sur les coefficients de régression. Par exemple, il se peut que deux coefficients différents doivent s’additionner à zéro, ou quelque chose de similaire. Vous pouvez aussi construire des tests d’hypothèse pour ce genre de contraintes, mais c’est un peu plus compliqué et la distribution d’échantillonnage pour F devenie une distribution connue sous le nom de distribution F non centrale, ce qui va bien au-delà de la portée de ce livre ! Tout ce que je veux faire, c’est vous alerter sur cette possibilité.↩︎