Chapitre 9 Tests d’hypothèses

Le processus d’induction est le processus d’adoption de la loi la plus simple qui peut être faite pour s’harmoniser avec notre expérience. Cependant, ce processus n’a pas de fondement logique, mais seulement psychologique. Il est clair qu’il n’y a aucune raison de croire que le cours des événements le plus simple se produira réellement. C’est une hypothèse que le soleil se lèvera demain : et cela signifie que nous ne savons pas s’il se lèvera. - Ludwig Wittgenstein⁵²

Dans le dernier chapitre, j’ai discuté des notions sous-jacentes à l’estimation, qui est l’une des deux « grandes notions » dans les statistiques inférentielles. Il est maintenant temps de nous pencher sur l’autre grande idée, à savoir la vérification des hypothèses. Dans sa forme la plus abstraite, la vérification d’hypothèses est vraiment une idée très simple. Le chercheur a une théorie sur le monde et veut déterminer si les données appuient ou non cette théorie. Cependant, les détails sont compliqués et la plupart des gens trouvent que la théorie de la vérification des hypothèses est la partie la plus frustrante des statistiques. La structure du chapitre est la suivante. Tout d’abord, je décrirai en détail le fonctionnement des tests d’hypothèses à l’aide d’un simple exemple de fonctionnement pour vous montrer comment un test d’hypothèse est « construit ». J’essaierai d’éviter d’être trop dogmatique en le faisant, et je me concentrerai plutôt sur la logique sous-jacente de la procédure de test.⁵³ Ensuite, je passerai un peu de temps à parler des différents dogmes, règles et hérésies qui entourent la théorie de la vérification des hypothèses.

9.1 Une ménagerie d’hypothèses

Finalement, nous finissons tous par succomber à la folie. Pour moi, ce jour arrivera quand je serai enfin promu professeur titulaire. En sécurité dans ma tour d’ivoire, heureusement protégée par la tenure, je pourrai enfin m’affranchir de mes sens (pour ainsi dire) et m’adonner à cette ligne de recherche psychologique la plus improductive, la recherche de la perception extrasensorielle (PES).⁵⁴

Supposons que ce jour glorieux soit arrivé. Ma première étude est une étude simple dans laquelle je cherche à tester si la clairvoyance existe. Chaque participant s’assoit à une table et se voit remettre une carte par un expérimentateur. La carte est noire d’un côté et blanche de l’autre. L’expérimentateur enlève la carte et la dépose sur une table dans une pièce adjacente. La carte est placée côté noir vers le haut ou côté blanc vers le haut complètement au hasard, la randomisation n’ayant lieu qu’après que l’expérimentateur ait quitté la salle avec le participant. Un deuxième expérimentateur arrive et demande au participant de quel côté de la carte est maintenant tournée vers le haut. C’est une expérience ponctuelle. Chaque personne ne voit qu’une seule carte et ne donne qu’une seule réponse, et à aucun moment le participant n’est réellement en contact avec quelqu’un qui connaît la bonne réponse. Mon ensemble de données est donc très simple. J’ai posé la question à N personnes et un certain nombre X d’entre elles ont donné la bonne réponse. Pour rendre les choses concrètes, supposons que j’ai testé N = 100 personnes et que X = 62 d’entre elles ont obtenu la bonne réponse. Un nombre étonnamment élevé, certes, mais est-il assez important pour que je me sente en sécurité en affirmant que j’ai trouvé des preuves pour l’ESP ? C’est dans ce cas qu’il est utile de vérifier les hypothèses. Cependant, avant de parler de la façon de vérifier les hypothèses, nous devons être clairs sur ce que nous entendons par hypothèses.

9.1.1 Hypothèses de recherche versus hypothèses statistiques

La première distinction que vous devez garder à l’esprit se situe entre les hypothèses de recherche et les hypothèses statistiques. Dans mon étude PES, mon objectif scientifique global est de démontrer que la clairvoyance existe. Dans cette situation, j’ai un objectif de recherche clair : j’espère découvrir des preuves de la PES. Dans d’autres situations, je pourrais même être beaucoup plus neutre que cela, je pourrais dire alors que mon but de recherche est de déterminer si la clairvoyance existe ou non. Peu importe la façon dont je veux me présenter, le point fondamental que j’essaie de faire valoir ici, c’est qu’une hypothèse de recherche implique la formulation d’une affirmation scientifique valable et vérifiable. Si vous êtes psychologue, vos hypothèses de recherche portent essentiellement sur les constructions psychologiques. L’une ou l’autre des hypothèses suivantes pourrait être considérée comme une hypothèse de recherche :

• Écouter de la musique réduit votre capacité à prêter attention à d’autres choses. Il s’agit d’une affirmation sur la relation causale entre deux concepts psychologiquement significatifs (écouter de la musique et faire attention aux choses), c’est donc une hypothèse de recherche parfaitement raisonnable.
• L’intelligence est liée à la personnalité. Comme la dernière, il s’agit d’une affirmation relationnelle sur deux constructions psychologiques (intelligence et personnalité), mais l’affirmation est plus faible : corrélationnelle et non causale.
• L’intelligence est la vitesse de traitement de l’information. Cette hypothèse a un tout autre caractère. Ce n’est pas du tout une affirmation relationnelle. C’est une affirmation ontologique sur le caractère fondamental de l’intelligence (et je suis presque sûr que c’est faux). Cela vaut la peine de s’étendre sur ce point en fait. Il est généralement plus facile de penser à la façon de construire des expériences pour vérifier des hypothèses de recherche de la forme « est-ce que X affecte Y ? » que pour répondre à des affirmations comme « qu’est-ce que X ? » Et dans la pratique, ce qui se passe habituellement, c’est que vous trouvez des moyens de tester les affirmations relationnelles qui découlent de vos affirmations ontologiques. Par exemple, si je crois que l’intelligence est la vitesse de traitement de l’information dans le cerveau, mes expériences consisteront souvent à rechercher des relations entre les mesures de l’intelligence et celles de la vitesse de traitement. Par conséquent, la plupart des questions quotidiennes de recherche ont tendance à être de nature relationnelle, mais elles sont presque toujours motivées par des questions ontologiques plus profondes sur l’état de la nature.

Notez qu’en pratique, mes hypothèses de recherche pourraient se chevaucher beaucoup. Mon but ultime dans l’expérience de PES pourrait être de tester une revendication ontologique comme « la PES existe », mais je pourrais me limiter opérationnellement à une hypothèse plus étroite comme « Certaines personnes peuvent « voir » des objets d’une manière clairvoyante ». Cela dit, il y a certaines choses qui ne comptent pas vraiment comme des hypothèses de recherche appropriées et ayant un sens :

• L’amour est un champ de bataille. C’est trop vague pour être testable. Bien qu’il soit acceptable qu’une hypothèse de recherche ait un certain degré d’imprécision, il doit être possible d’opérationnaliser vos idées théoriques. Je ne suis peut-être pas assez créatif pour le voir, mais je ne vois pas comment cela peut être converti en un plan de recherche concret. Si c’est vrai, ce n’est pas une hypothèse de recherche scientifique, c’est une chanson pop. Ça ne veut pas dire que ce n’est pas intéressant. Beaucoup de questions profondes que se posent les humains entrent dans cette catégorie. Peut-être qu’un jour la science sera capable de construire des théories vérifiables de l’amour, ou de tester si Dieu existe, et ainsi de suite. Mais pour l’instant, nous ne pouvons pas, et je ne parierais pas sur une approche scientifique satisfaisante de l’un ou de l’autre.
• La première règle du club de tautologie est la première règle du club de tautologie. Il ne s’agit pas d’une affirmation de fond de quelque nature que ce soit. C’est vrai par définition. Aucun état de nature concevable ne pourrait être incompatible avec cette affirmation. Nous disons qu’il s’agit d’une hypothèse infalsifiable et qu’en tant que telle, elle ne relève pas du domaine de la science. Quoi que vous fassiez d’autre en science, vos affirmations doivent avoir la possibilité d’être réfutées.
• Plus de gens dans mon expérience diront « oui » que « non ». Celle-ci ne constitue pas une hypothèse de recherche parce qu’il s’agit d’une affirmation au sujet de l’ensemble des données, et non au sujet de la psychologie (à moins, bien sûr, que votre vraie question de recherche soit de savoir si les gens ont une sorte de biais du « oui »). En fait, cette hypothèse commence à ressembler davantage à une hypothèse statistique qu’à une hypothèse de recherche.

Comme vous pouvez le constater, les hypothèses de recherche peuvent parfois être quelque peu confuses et, en fin de compte, ce sont des affirmations scientifiques. Les hypothèses statistiques ne sont ni l’une ni l’autre de ces choses. Les hypothèses statistiques doivent être mathématiquement précises et correspondre à des affirmations précises sur les caractéristiques du mécanisme de production des données (c.-à-d. la « population »). Malgré tout, l’intention est que les hypothèses statistiques aient une relation claire avec les hypothèses de recherche qui vous tiennent à cœur ! Par exemple, dans mon étude sur la PES, mon hypothèse de recherche est que certaines personnes sont capables de voir à travers les murs ou autre. Ce que je veux faire, c’est « mapper » ceci sur une affirmation sur la façon dont les données ont été générées. Réfléchissons donc à ce que pourrait être cette déclaration. La quantité qui m’intéresse dans l’expérience est P(correct), la probabilité vraie mais inconnue avec laquelle les participants à mon expérience répondent correctement à la question. Utilisons la lettre grecque \(\theta\) (thêta) pour faire référence à cette probabilité. Voici quatre hypothèses statistiques différentes :

• Si la PES n’existe pas et si mon expérience est bien conçue, mes participants ne font que deviner. Je m’attends donc à ce qu’ils réussissent la moitié du temps et donc mon hypothèse statistique est que la vraie probabilité de choisir correctement est \(\theta=0,5\).

• Supposons également qu’il existe une PES et que les participants puissent voir la carte. Si c’est vrai que les gens feront mieux que le hasard et l’hypothèse statistique est que \(\theta>0,5\).

• Une troisième possibilité est que la PES existe, mais les couleurs sont toutes inversées et les gens ne s’en rendent pas compte (ok, c’est dingue, mais on ne sait jamais). Si c’est comme ça que ça marche, on s’attendrait à ce que la performance des gens soit inférieure au hasard. Cela correspondrait à une hypothèse statistique selon laquelle \(\theta<0.5\)

• Enfin, supposons que la PES existe mais que je ne sais pas si les gens voient la bonne ou la mauvaise couleur. Dans ce cas, la seule affirmation que je pourrais faire au sujet des données serait que la probabilité de faire la bonne réponse n’est pas égale à 0,5. Ceci correspond à l’hypothèse statistique que \(\theta\neq{0.5}\).

Ce sont tous des exemples légitimes d’hypothèses statistiques parce qu’il s’agit d’énoncés concernant un paramètre de population et qu’ils sont liés de façon significative à mon expérience.

Ce qui ressort clairement de cette discussion, je l’espère, c’est que lorsqu’on tente d’élaborer un test d’hypothèse statistique, le chercheur a en fait deux hypothèses bien distinctes à considérer. D’abord, il a une hypothèse de recherche (une affirmation sur la psychologie), et cela correspond ensuite à une hypothèse statistique (une affirmation sur la population génératrice de données). Dans mon exemple de PES, il pourrait s’agir de :

Hypothèse de recherche de Dani : « La PES existe »
Hypothèse statistique de Dani : \(\theta\neq{0.5}\)

Le point clé à comprendre est celui-ci. Un test d’hypothèse statistique est un test de l’hypothèse statistique et non de l’hypothèse de recherche. Si votre étude est mal conçue, le lien entre votre hypothèse de recherche et votre hypothèse statistique est rompu. Pour donner un exemple stupide, supposons que mon étude sur la PES ait été menée dans une situation où le participant peut réellement voir la carte se refléter dans une fenêtre. Si cela se produit, je serais en mesure de trouver des preuves très solides que \(\theta\neq{0.5}\), mais cela ne nous dirait rien sur la question de savoir si « la PES existe ».

9.1.2 Hypothèses nulles et hypothèses alternatives

Pour l’instant, tout va bien. J’ai une hypothèse de recherche qui correspond à ce que je veux croire au sujet du monde, et je peux l’appliquer à une hypothèse statistique qui correspond à ce que je veux croire sur la façon dont les données ont été générées. C’est à ce stade que les choses deviennent quelque peu contre-intuitives pour beaucoup de gens. Parce que ce que je m’apprête à faire, c’est inventer une nouvelle hypothèse statistique (l’hypothèse « nulle », H0) qui correspond exactement à l’opposé de ce que je veux croire, puis me concentrer exclusivement sur celle-ci presque au détriment de ce qui m’intéresse réellement (qu’on appelle maintenant l’hypothèse « alternative », H1). Dans notre exemple de PES, l’hypothèse nulle est que \(\theta=0.5\), puisque c’est ce à quoi on pourrait s’attendre si la PES n’existait pas. Mon espoir, bien sûr, est que PES soit totalement vraie et donc l’alternative à cette hypothèse nulle est \(\theta\neq{0.5}\) aussi. Fondamentalement, ce que nous faisons ici est de diviser les valeurs possibles de \(\theta\) en deux groupes : ces valeurs dont j’espère vraiment qu’elles ne sont pas vraies (la valeur nulle), et les valeurs dont je serais heureux si elles s’avéraient exactes (l’alternative). Ce faisant, il est important de comprendre que le but d’un test d’hypothèse n’est pas de montrer que l’hypothèse alternative est (probablement) vraie. Le but est de montrer que l’hypothèse nulle est (probablement) fausse. La plupart des gens trouvent ça plutôt bizarre.

La meilleure façon d’y penser, d’après mon expérience, est d’imaginer qu’un test d’hypothèse est un procès criminel⁵⁵, le procès de l’hypothèse nulle. L’hypothèse nulle est l’accusé, le chercheur est le procureur et le test statistique lui-même est le juge. Tout comme dans un procès criminel, il y a présomption d’innocence. L’hypothèse nulle est considérée comme vraie à moins que vous, le chercheur, ne puissiez prouver hors de tout doute raisonnable qu’elle est fausse. Vous êtes libre de concevoir votre expérience comme bon vous semble (dans les limites du raisonnable, évidemment !) et votre objectif est de maximiser les chances que les données aboutissent à une condamnation pour le crime d’être faux. Le piège, c’est que le test statistique établit les règles du procès et que ces règles sont conçues pour protéger l’hypothèse nulle, notamment pour s’assurer que si l’hypothèse nulle est vraie, les chances d’une fausse condamnation sont faibles. C’est très important. Après tout, l’hypothèse nulle n’a pas d’avocat, et étant donné que le chercheur essaie désespérément de prouver qu’elle est fausse, il faut la protéger.

9.2 Deux types d’erreurs

Avant d’entrer dans les détails sur la façon dont un test statistique est construit, il est utile de comprendre la philosophie qui le sous-tend. J’y ai fait allusion en soulignant la similitude entre un test d’hypothèse nulle et un procès criminel, mais je dois maintenant être explicite. Idéalement, nous aimerions construire notre test de manière à ne jamais faire d’erreurs. Malheureusement, comme le monde est en désordre, ce n’est jamais possible. Parfois, on est vraiment malchanceux. Par exemple, supposez que vous tirez une pièce de monnaie 10 fois de suite et qu’elle tombe sur face 10 fois de suite. Cela semble être une preuve très solide pour conclure que la pièce est biaisée, mais bien sûr, il y a une chance sur 1024 que cela se produise même si la pièce était totalement juste. En d’autres termes, dans la vraie vie, nous devons toujours accepter qu’il y a une chance que nous ayons commis une erreur. Par conséquent, l’objectif des tests d’hypothèses statistiques n’est pas d’éliminer les erreurs, mais de les minimiser.

A ce stade, nous devons être un peu plus précis sur ce que nous entendons par « erreurs ». D’abord, disons ce qui est évident. Soit que l’hypothèse nulle est vraie, soit qu’elle est fausse, et notre test retiendra ou rejettera l’hypothèse nulle.⁵⁶ Ainsi, comme l’illustre le tableau ci-dessous, après avoir effectué le test et fait notre choix, l’une des quatre situations suivantes aurait pu se produire :

	retenir H0	rejeter H0
H0 est vrai	décision juste	erreur (type I)
H0 est faux	erreur (type II)	décision juste

Par conséquent, il y a deux types d’erreurs différents. Si nous rejetons une hypothèse nulle qui est en fait vraie, alors nous avons fait une erreur de type I. Par contre, si nous retenons l’hypothèse nulle alors qu’elle est en fait fausse, nous avons fait une erreur de type II.

Vous vous souvenez quand j’ai dit que les tests statistiques étaient un peu comme un procès criminel ? Eh bien, je le pensais vraiment. Un procès criminel exige que vous établissiez « hors de tout doute raisonnable » que l’accusé l’a commis. Toutes les règles de preuve sont (du moins en théorie) conçues pour s’assurer qu’il n’y a (presque) aucune chance de condamner à tort un suspect innocent. Le procès vise à protéger les droits de l’accusé, comme l’a dit le juriste anglais William Blackstone, « il vaut mieux que dix coupables s’échappent que celui qu’un innocent qui souffre ». En d’autres termes, un procès criminel ne traite pas les deux types d’erreur de la même façon. Punir l’innocent est considéré comme bien pire que de libérer le coupable. Un test statistique est à peu près la même chose. Le principe de conception le plus important du test est de contrôler la probabilité d’une erreur de type I, pour la maintenir en dessous d’une probabilité fixe. Cette probabilité, qui est dénommée \(\alpha\), est appelée le niveau de signification du test. Et je le répète encore une fois, parce que c’est tellement central dans l’ensemble du dispositif, un test d’hypothèse est dit avoir un niveau de signification \(\alpha\) si le taux d’erreur de type I n’est pas supérieur à \(\alpha\)

Qu’en est-il alors du taux d’erreur de type II ? Eh bien, nous aimerions aussi les garder sous contrôle, et nous indiquons cette probabilité par \(\beta\). Cependant, il est beaucoup plus courant de se référer à la puissance du test, c’est-à-dire la probabilité avec laquelle nous rejetons une hypothèse nulle quand elle est vraiment fausse, qui est \(1-\beta\). Pour aider à garder cela en tête, voici de nouveau le même tableau mais avec les chiffres pertinents ajoutés :

	retenir H0	rejeter H0
H0 est vrai	\(1-\alpha\) (probabilité de conservation correcte)	\(\alpha\) (taux d’erreur de type I)
H0 est faux	\(\beta\) (taux d’erreur de type II)	\(1-\beta\) (puissance du test)

Un test d’hypothèse « puissant » est un test qui a une petite valeur de \(\beta\), tout en gardant \(\alpha\) fixé au (petit) niveau souhaité. Par convention, les scientifiques utilisent trois niveaux différents de \(\alpha\) : .05, .01 et .001. Notez l’asymétrie ici ; les tests sont conçus pour s’assurer que le niveau de \(\alpha\) est maintenu petit mais il n’y a aucune garantie correspondante concernant \(\beta\). Nous aimerions certainement que le taux d’erreur de type II soit petit et nous essayons de concevoir des tests qui le gardent petit, mais ceci est généralement secondaire au besoin écrasant de contrôler le taux d’erreur du type I. Comme l’aurait dit Blackstone s’il avait été statisticien, il est « préférable de retenir 10 fausses hypothèses nulles que d’en rejeter une seule vraie ». Pour être honnête, je ne sais pas si je suis d’accord avec cette philosophie. Il y a des situations où je pense que c’est logique, et d’autres où ce n’est pas le cas, mais ce n’est ni ici ni là. C’est ainsi que les tests sont construits.

9.3 Statistiques des tests et distributions d’échantillonnage

À ce stade, nous devons commencer à parler plus précisément de la façon dont un test d’hypothèse est construit. Pour ce faire, revenons à l’exemple de la PES. Ignorons les données réelles que nous avons obtenues, pour l’instant, et pensons à la structure de l’expérience. Quels que soient les chiffres réels, la forme des données est que X sur N personnes ont correctement identifié la couleur de la carte cachée. De plus, supposons pour l’instant que l’hypothèse nulle soit vraie, que la PES n’existe pas et que la vraie probabilité que quelqu’un choisisse la bonne couleur soit exactement \(\theta=0.5\). À quoi devraient ressembler les données ? Évidemment, on s’attendrait à ce que la proportion de personnes qui donnent la bonne réponse soit assez près de 50 p. 100. Ou, pour exprimer cela en termes plus mathématiques, nous dirions que X/N est d’environ 0,5. Bien sûr, on ne s’attendrait pas à ce que cette fraction soit exactement de 0,5. Si, par exemple, on testait N = 100 personnes et que X = 53 d’entre elles avaient la bonne réponse, on serait probablement forcé d’admettre que les données sont assez cohérentes avec l’hypothèse nulle. D’un autre côté, si X = 99 de nos participants répondaient correctement, nous serions assez confiants que l’hypothèse nulle est fausse. De même, si seulement X = 3 personnes obtenaient la bonne réponse, nous serions tout aussi confiants que l’hypothèse nulle est fausse. Soyons un peu plus techniques à ce sujet. Nous avons une quantité X que nous pouvons calculer en regardant nos données. Après avoir examiné la valeur de X, nous décidons s’il faut croire que l’hypothèse nulle est correcte ou rejeter l’hypothèse nulle en faveur de l’alternative. Le nom de cette valeur que nous calculons pour guider nos choix est une statistique de test.

Après avoir choisi une statistique de test, l’étape suivante consiste à indiquer précisément quelles valeurs de la statistique de test entraîneraient le rejet de l’hypothèse nulle et quelles valeurs nous inciteraient à la conserver. Pour ce faire, nous devons déterminer quelle serait la distribution d’échantillonnage de la statistique de test si l’hypothèse nulle était réellement vraie (nous avons parlé des distributions d’échantillonnage plus tôt dans la section 8.3.1). Pourquoi en avons-nous besoin ? Parce que cette distribution nous dit exactement quelles valeurs de X notre hypothèse nulle nous amènerait à attendre. Et, par conséquent, nous pouvons utiliser cette distribution comme outil pour évaluer dans quelle mesure l’hypothèse nulle correspond à nos données.

Comment détermine-t-on réellement la distribution d’échantillonnage de la statistique du test ? Pour beaucoup de tests d’hypothèse, cette étape est en fait assez compliquée, et plus tard dans le livre, vous me verrez être un peu évasif à ce sujet pour certains tests (pour certains d’entre eux, je ne les comprends même pas moi-même). Cependant, c’est parfois très facile. Et, heureusement pour nous, notre exemple de PES nous fournit l’un des cas les plus faciles. Notre paramètre de population \(\theta\) n’est que la probabilité globale que les gens répondent correctement lorsqu’on leur pose la question, et notre statistique de test X est le nombre de personnes qui l’ont fait sur un échantillon de N.

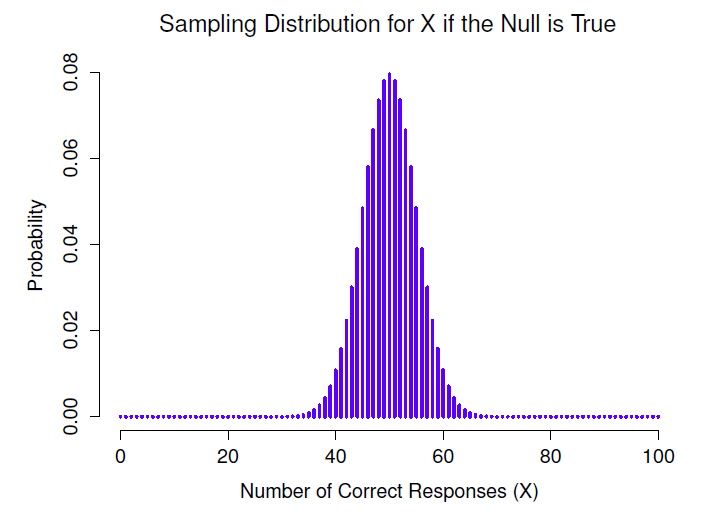
Figure 9‑1 : La distribution d’échantillonnage pour notre statistique de test X lorsque l’hypothèse nulle est vraie. Pour notre scénario ESP, il s’agit d’une distribution binomiale. Comme on pouvait s’y attendre, puisque l’hypothèse nulle indique que la probabilité d’une réponse correcte est \(\theta=0,5\), la distribution d’échantillonnage indique que la valeur la plus probable est 50 (sur 100) bonnes réponses. La plus grande partie de la masse de probabilité se situe entre 40 et 60.

Nous avons déjà vu une distribution comme celle-ci à la section 7.4, et c’est exactement la même que la distribution binomiale ! Ainsi, pour utiliser la notation et la terminologie que j’ai présentées dans cette section, nous dirions que l’hypothèse nulle prédit que X est distribué de façon binomiale, ce qui est écrit

\[ X\sim Binomiale\ (\theta,N) \]

Puisque l’hypothèse nulle indique que \(\theta=0,5\) et que notre expérience compte N = 100 personnes, nous avons la distribution d’échantillonnage dont nous avons besoin. Cette distribution d’échantillonnage est illustrée à la Figure 9‑1. Sans surprise, l’hypothèse nulle dit que X = 50 est le résultat le plus probable, et qu’il est presque certain que nous verrons entre 40 et 60 bonnes réponses.

9.4 Prendre des décisions

Bon, nous sommes très près d’en avoir fini. Nous avons construit une statistique de test (X) et nous avons choisi cette statistique de test de telle manière que nous sommes assez confiants que si X est proche de N/2 alors nous devrions conserver l’hypothèse nulle, sinon nous devrions la rejeter. La question qui demeure est la suivante. Quelles valeurs exactes de la statistique du test faut-il associer à l’hypothèse nulle, et quelles valeurs vont exactement avec l’hypothèse alternative ? Dans mon étude ESP, par exemple, j’ai observé une valeur de X=62. Quelle décision devrais-je prendre ? Devrais-je choisir de croire l’hypothèse nulle ou l’hypothèse alternative ?

9.4.1 Régions critiques et valeurs critiques

Pour répondre à cette question, nous devons introduire le concept de région critique pour la statistique de test X. La région critique du test correspond aux valeurs de X qui nous amèneraient à rejeter une hypothèse nulle (c’est pourquoi la région critique est aussi parfois appelée région de rejet). Comment trouver cette région critique ? Eh bien, considérons ce que nous savons :

• X doit être très grand ou très petit pour rejeter l’hypothèse nulle.
• Si l’hypothèse nulle est vraie, la distribution d’échantillonnage de X est Binomiale (0,5, N).
• Si \(\alpha=0.5\), la région critique doit couvrir 5% de cette distribution d’échantillonnage.

Il est important que vous compreniez bien ce dernier point. La région critique correspond aux valeurs de X pour lesquelles on rejetterait l’hypothèse nulle, et la distribution d’échantillonnage en question décrit la probabilité d’obtenir une valeur particulière de X si l’hypothèse nulle était effectivement vraie. Supposons maintenant que nous choisissions une région critique qui couvre 20% de la distribution d’échantillonnage, et supposons que l’hypothèse nulle soit vraie. Quelle serait la probabilité d’un rejet incorrect de l’annulation ? La réponse est bien sûr 20 %. Et, par conséquent, nous aurions construit un test ayant un niveau \(\alpha\) de 0,2. Si nous voulons \(\alpha=0.5\), la région critique ne peut couvrir que 5% de la distribution d’échantillonnage de notre statistique de test.

Il s’avère que ces trois choses résolvent le problème de façon unique. Notre région critique se compose des valeurs les plus extrêmes, connues sous le nom de queues de la distribution. C’est ce qu’illustre la Figure 9‑2. Si nous voulons \(\alpha=0.5\) alors nos régions critiques correspondent à \(X\leqslant 40\) et \(X\geqslant 60\) .⁵⁷ C’est-à-dire que, si le nombre de personnes qui disent «vrai» se situe entre 41 et 59, alors nous devrions retenir l’hypothèse nulle. Si le nombre est compris entre 0 et 40, ou entre 60 et 100, alors nous devrions rejeter l’hypothèse nulle. Les nombres 40 et 60 sont souvent appelés valeurs critiques car ils définissent les limites de la région critique.

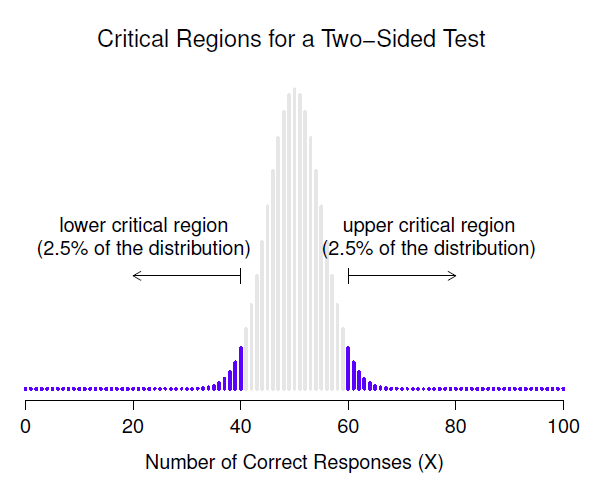
Figure 9‑2 : La région critique associée au test d’hypothèse pour l’étude ESP, pour un test d’hypothèse avec un niveau de signification de \(\alpha=.05\). Le graphique montre la distribution d’échantillonnage de X sous l’hypothèse nulle (c.-à-d. identique à la Figure 9‑1). Les barres grises correspondent aux valeurs de X pour lesquelles on retiendrait l’hypothèse nulle. Les barres bleues (plus foncées) indiquent la région critique, ces valeurs de X pour lesquelles nous rejetterions la valeur nulle. Étant donné que l’hypothèse alternative est bilatérale (c.-à-d. qu’elle permet à la fois \(\theta<0,5\) et \(\theta>0,5\)), la région critique couvre les deux queues de la distribution. Pour assurer un niveau de .05 à \(\alpha\), nous devons nous assurer que chacune des deux régions englobe 2,5 % de la distribution de l’échantillonnage.

À ce stade, notre test d’hypothèse est pratiquement terminé :

1. nous choisissons un niveau \(\alpha\) (p. ex. \(\alpha=.05\)) ;
2. calculons des statistiques de test (p. ex., X) qui permettent de bien comparer H₀ à H₁ (d’un point de vue qui ai su sens) ;
3. déterminons la distribution d’échantillonnage de la statistique de test en supposant que l’hypothèse nulle est vraie (dans ce cas, c’est la binomiale) ; puis
4. calculons la région critique qui produit un niveau approprié de \(\alpha\) (0-40 et 60-100).

Il ne nous reste plus qu’à calculer la valeur de la statistique du test pour les données réelles (par exemple, X = 62) et la comparer aux valeurs critiques pour prendre notre décision. Puisque 62 est supérieur à la valeur critique de 60, nous rejetterions l’hypothèse nulle. Ou, pour le formuler un peu différemment, nous disons que le test a produit un résultat statistiquement significatif.

9.4.2 Note sur la « signification » statistique

Comme d’autres techniques occultes de divination, la méthode statistique a un jargon privé délibérément inventé pour cacher ses méthodes aux non-praticiens. - Attribué à G. O. Ashley⁵⁸

Une très brève digression s’impose à ce stade, en ce qui concerne le mot « significatif ». Le concept de signification statistique est en fait très simple, mais il porte un nom très malheureux. Si les données nous permettent de rejeter l’hypothèse nulle, nous disons que « le résultat est statistiquement significatif », ce qui est souvent réduit à « le résultat est significatif ». Cette terminologie est plutôt ancienne et remonte à une époque où « significatif » signifiait simplement quelque chose comme « signifié », plutôt que sa signification moderne qui est beaucoup plus proche de « important ». En conséquence, beaucoup de lecteurs modernes sont très confus lorsqu’ils commencent à apprendre les statistiques parce qu’ils pensent qu’un « résultat significatif » doit être un résultat important. Ça ne veut pas dire ça du tout. Tout ce que « statistiquement significatif » signifie, c’est que les données nous ont permis de rejeter une hypothèse nulle. La question de savoir si le résultat est réellement important dans le monde réel est une question très différente et dépend de toutes sortes d’autres choses.

9.4.3 La différence entre les tests unilatéraux et bilatéraux

Il y a encore une chose que je tiens à souligner au sujet du test d’hypothèse que je viens de construire. Si on prend un moment pour réfléchir aux hypothèses statistiques que j’ai utilisées, nous remarquons que l’hypothèse alternative couvre à la fois la possibilité que \(\theta < .5\) et la possibilité que \(\theta > .5\).

\(\text{H}_{0} : \theta=.5\) \(\text{H}_{1} : \theta\neq{.5}\)

C’est logique si on pense vraiment que la PES pourrait produire soit une performance supérieure au hasard, soit une performance inférieure au hasard (et il y a des gens qui pensent cela). En langage statistique, il s’agit d’un exemple de test bilatéral. On l’appelle ainsi parce que l’hypothèse alternative couvre la zone des deux « côtés » de l’hypothèse nulle, et par conséquent la région critique du test couvre les deux queues de la distribution d’échantillonnage (2,5% de chaque côté si \(\alpha=0.5\)), comme illustré précédemment dans la Figure 9‑2.

Cependant, ce n’est pas la seule possibilité. Je ne suis prêt à croire en la PES que si elle produit de meilleures performances que le hasard. Si c’est le cas, alors mon hypothèse alternative ne couvrirait que la possibilité que \(\theta>.5\), et par conséquent l’hypothèse nulle devient \(\theta<.5\)

\(\text{H}_{0} : \theta\leqslant.5\) \(\text{H}_{1} : \theta\>.5\)

Lorsque cela se produit, nous avons ce qu’on appelle un test unilatéral et la région critique ne couvre qu’une seule queue de la distribution d’échantillonnage. C’est ce qu’illustre la Figure 9‑3.

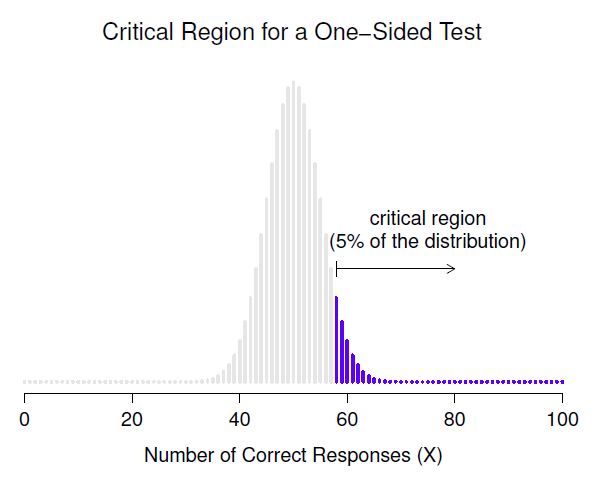
Figure 9‑3 : La région critique pour un essai unilatéral. Dans ce cas, l’hypothèse alternative est que \(\theta>.5\) de sorte que nous ne rejetterions que l’hypothèse nulle pour les grandes valeurs de X. Par conséquent, la région critique ne couvre que la partie supérieure de la queue de la distribution d’échantillonnage, en particulier les 5 % supérieurs de la distribution. Comparez cela à la version bilatérale de la Figure 9.2.

9.5 La valeur p d’un test

Dans un sens, notre test d’hypothèse est complet. Nous avons construit une statistique de test, calculé sa distribution d’échantillonnage si l’hypothèse nulle est vraie, et ensuite construit la région critique pour le test. Néanmoins, j’ai en fait omis le nombre le plus important de tous, la valeur p. C’est à ce sujet que nous passons maintenant. Il y a deux façons quelque peu différentes d’interpréter une valeur p, l’une proposée par Sir Ronald Fisher et l’autre par Jerzy Neyman. Les deux versions sont légitimes, bien qu’elles reflètent des façons très différentes de concevoir les tests d’hypothèse. La plupart des manuels d’introduction tendent à ne donner que la version de Fisher, mais je pense que c’est un peu dommage. À mon avis, la version de Neyman est plus propre et reflète mieux la logique du test de l’hypothèse nulle. Mais vous n’êtes peut-être pas d’accord, alors j’ai inclus les deux. Je vais commencer par la version de Neyman.

9.5.1 Une vision plus douce de la prise de décision

L’un des problèmes de la procédure de vérification des hypothèses que j’ai décrite est qu’elle ne fait aucune distinction entre un résultat qui est « à peine significatif » et ceux qui sont « très significatifs ». Par exemple, dans mon étude sur le PES, les données que j’ai obtenues tombaient tout juste de à l’intérieur de la région critique, alors j’ai obtenu un effet significatif, mais c’était assez limite. Par contre, supposons que je fasse une étude dans laquelle X = 97 de mes N=100 participants ont obtenu la bonne réponse. Ce serait évidemment significatif aussi, mais ma marge est beaucoup plus grande, de sorte qu’il n’y a vraiment aucune ambiguïté à ce sujet. La procédure que j’ai déjà décrite ne fait aucune distinction entre les deux. Si j’adopte la convention standard d’autoriser \(\alpha=.05\) comme taux d’erreur de type I acceptable, ces deux résultats sont significatifs.

C’est là que la valeur p est utile. Pour comprendre son fonctionnement, supposons que nous ayons effectué de nombreux tests d’hypothèses sur le même ensemble de données, mais avec une valeur différente de \(\alpha\) dans chaque cas. Lorsque nous faisons cela pour mes données d’origine sur la PES, nous obtenons quelque chose comme ceci

Valeur de \(\alpha\)	0.05	0.04	0.03	0.02	0.01
Rejeter H0 ?	Oui	Oui	Oui	Non	Non

Quand on teste les données de la PES (X = 62 succès sur N = 100 observations), en utilisant les niveaux \(\alpha\) de .03 et plus, on se retrouve toujours à rejeter l’hypothèse nulle. Pour les niveaux de \(\alpha\) de .02 et moins, nous finissons toujours par conserver l’hypothèse nulle. Par conséquent, quelque part entre .02 et.03, il doit y avoir une valeur minimale de \(\alpha\) qui nous permettrait de rejeter l’hypothèse nulle pour ces données. C’est la valeur p. Il s’avère que les données de la PES, on a p = .021. En bref,

p est défini comme étant le plus petit taux d’erreur de type I (\(\alpha\)) que vous devez être prêt à tolérer si vous voulez rejeter l’hypothèse nulle.

S’il s’avère que p décrit un taux d’erreur que vous trouvez intolérable, alors vous devez conserver la valeur nulle. Si vous êtes à l’aise avec un taux d’erreur égal à p, vous pouvez rejeter l’hypothèse nulle en faveur de votre alternative préférée.

En effet, p est un résumé de tous les tests d’hypothèses possibles que vous auriez pu faire, à travers toutes les valeurs possibles de \(\alpha\) Et par conséquent, cela a pour effet de « moduler » notre processus de décision. Pour les tests dans lesquels \(p \leq \alpha\) vous auriez rejeté l’hypothèse nulle, alors que pour les tests dans lesquels \(p > \alpha\) vous auriez retenu l’hypothèse nulle. Dans mon étude sur la PES j’ai obtenu X = 62 et par conséquent j’ai obtenu p =.021. Le taux d’erreur que je dois tolérer est donc de 2,1 p. 100. Par contre, supposons que mon expérience ait donné X = 97. Qu’advient-il de ma valeur p maintenant ? Cette fois-ci, il est réduit à p = 1.36*10-25, qui est un taux d’erreur de type I⁵⁹ minuscule. Pour ce second cas, je serais en mesure de rejeter l’hypothèse nulle avec beaucoup plus de confiance, parce qu’il me suffit d’être « disposé » à tolérer un taux d’erreur de type I d’environ 1 sur 10 trillions de milliards pour justifier ma décision de rejeter.

9.5.2 La probabilité de données extrêmes

La deuxième définition de la p-value vient de Sir Ronald Fisher, et c’est en fait celle-ci que vous avez tendance à voir dans la plupart des manuels d’introduction aux statistiques. Remarquez comment, lorsque j’ai construit la région critique, elle correspondait aux queues (c’est-à-dire aux valeurs extrêmes) de la distribution d’échantillonnage ? Ce n’est pas une coïncidence, presque tous les « bons » tests ont cette caractéristique (bon dans le sens de minimiser notre taux d’erreur de type II, \(\beta\)). La raison en est qu’une bonne région critique correspond presque toujours aux valeurs de la statistique du test qui sont les moins susceptibles d’être observées si l’hypothèse nulle est vraie. Si cette règle est vraie, nous pouvons définir la valeur p comme la probabilité d’observer une statistique de test qui est au moins aussi extrême que celle que nous avons effectivement obtenue. En d’autres termes, si les données sont extrêmement peu plausibles selon l’hypothèse nulle, alors l’hypothèse nulle est probablement fausse.

9.5.3 Une erreur courante

Bien, vous pouvez donc voir qu’il y a deux façons plutôt différentes mais légitimes d’interpréter la valeur p, l’une fondée sur l’approche de Neyman pour vérifier les hypothèses et l’autre sur celle de Fisher. Malheureusement, il y a une troisième explication que les gens donnent parfois, surtout lorsqu’ils apprennent des statistiques pour la première fois, et celle-ci est absolument et complètement fausse. Cette approche erronée consiste à désigner la valeur p comme « la probabilité que l’hypothèse nulle soit vraie ». C’est une façon intuitive et attrayante de penser, mais elle est erronée à deux égards. Premièrement, le test d’hypothèse nulle est un outil fréquentiste et l’approche fréquentiste de la probabilité ne vous permet pas d’attribuer des probabilités à l’hypothèse nulle. Selon cette conception de la probabilité, l’hypothèse nulle est soit vraie, soit fausse, elle ne peut pas avoir « 5% de chance » d’être vraie. Deuxièmement, même dans l’approche bayésienne, qui permet d’assigner des probabilités aux hypothèses, la valeur p ne correspondrait pas à la probabilité que la valeur nulle soit vraie. Cette interprétation est tout à fait incompatible avec les mathématiques du calcul de la valeur p. En clair, malgré l’attrait intuitif d’une telle façon de penser, il n’y a aucune justification pour interpréter une valeur p de cette façon. Ne jamais le faire.

9.6 Communication des résultats d’un test d’hypothèse

Lorsque vous rédigez les résultats d’un test d’hypothèse, il y a habituellement plusieurs éléments d’information que vous devez rapporter, mais cela varie beaucoup d’un test à l’autre. Tout au long du reste du livre, je vais passer un peu de temps à parler de la façon de rapporter les résultats des différents tests (voir la Section 10.1.9 pour un exemple particulièrement détaillé), afin que vous puissiez vous faire une idée de la façon dont cela se fait habituellement. Cependant, peu importe le test que vous faites, la seule chose que vous devez toujours faire est de dire quelque chose sur la valeur p et si le résultat est significatif ou non.

Le fait que vous deviez le faire n’est pas surprenant, c’est tout l’intérêt de faire le test. Ce qui peut surprendre, c’est le fait qu’il y a une certaine controverse sur la façon exacte de faire les choses. Si l’on laisse de côté les personnes qui ne sont pas du tout d’accord avec l’ensemble du cadre qui sous-tend les tests d’hypothèse nulle, il existe une certaine tension quant à savoir s’il faut déclarer ou non la valeur exacte de p que vous avez obtenue, ou si vous devez déclarer seulement ce \(p < \alpha\) pour un niveau de signification que vous avez préalablement choisi (p. ex., p<.05).

9.6.1 La question

Pour comprendre pourquoi il s’agit d’un problème, le point clé à comprendre est que les valeurs p sont terriblement pratiques. En pratique, le fait que nous puissions calculer une valeur p signifie que nous n’avons pas besoin du tout de spécifier un niveau \(\alpha\) pour exécuter le test. A la place, vous pouvez calculer votre valeur p et l’interpréter directement. Si vous obtenez p = 0,062, cela signifie que vous devez être prêt à tolérer un taux d’erreur de type I de 6,2 % pour justifier le rejet de la valeur nulle. Si vous trouvez personnellement 6,2 % intolérable, vous conservez l’hypothèse nulle. Par conséquent, l’argument est le suivant : pourquoi ne pas simplement déclarer la valeur réelle de p et laisser au lecteur le soin de se faire sa propre opinion sur ce qu’est un taux d’erreur de type I acceptable ? Cette approche a le grand avantage « d’adoucir » le processus de prise de décision. En fait, si vous acceptez la définition de Neyman de p, c’est le sens même de la valeur de p. Nous n’avons plus un niveau de signification fixe de \(\alpha=.05\) comme la limite qui sépare les décisions « accepter » et « rejeter », ce qui élimine le problème plutôt pathologique de devoir traiter p=.051 d’une manière fondamentalement différente de p =.049.

Cette flexibilité est à la fois l’avantage et l’inconvénient de la valeur p. La raison pour laquelle beaucoup de gens n’aiment pas l’idée de rapporter une valeur p exacte est que cela donne un peu trop de liberté au chercheur. En particulier, il vous permet de changer d’avis sur la tolérance aux erreurs que vous êtes prêt à tolérer après avoir examiné les données. Prenons, par exemple, mon expérience sur la PES. Supposons que j’ai fait mon test et que j’ai obtenu une valeur p de 0,09. Dois-je accepter ou rejeter ? Maintenant, pour être honnête, je n’ai pas encore pris la peine de penser au niveau d’erreur de type I que je suis « vraiment » prêt à accepter. Je n’ai pas d’opinion à ce sujet. Mais j’ai une opinion sur l’existence ou non de la PES, et j’ai certainement une opinion sur le fait que mes recherches devraient être publiées dans une revue scientifique réputée. Et étonnamment, maintenant que j’ai examiné les données, je commence à penser qu’un taux d’erreur de 9 % n’est pas si mauvais, surtout si on le compare au fait qu’il serait ennuyeux d’avoir à reconnaitre publiquement que mon expérience a échoué. Donc, pour ne pas avoir l’air d’avoir tout inventé après coup, je dis maintenant que mon \(\alpha\) est .1, avec l’argument qu’un taux d’erreur de type I de 10% n’est pas trop mauvais et à ce niveau mon test est significatif ! J’ai gagné.

En d’autres termes, ce qui m’inquiète ici, c’est qu’ayant les meilleures intentions et étant la plus honnête des personnes, la tentation de cacher un peu les choses ici et là est vraiment, vraiment forte. Comme tous ceux qui ont déjà fait une expérience peuvent en témoigner, c’est un processus long et difficile et on s’attache souvent beaucoup à ses hypothèses. C’est difficile de laisser aller et d’admettre que l’expérience n’a pas permis de trouver ce que vous vouliez trouver. Et c’est là que réside le danger. Si nous utilisons la valeur p « brute », les gens commenceront à interpréter les données en fonction de ce qu’ils veulent croire, et non de ce que les données disent réellement et, si nous le permettons, pourquoi nous donnons-nous la peine de faire de la science ? Pourquoi ne pas laisser tout le monde croire ce qu’il veut de n’importe quoi, quels que soient les faits ? C’est un peu extrême, mais c’est de là que vient l’inquiétude. Selon ce point de vue, vous devez vraiment spécifier votre valeur \(\alpha\) à l’avance et ensuite seulement indiquer si le test était significatif ou non. C’est le seul moyen de rester honnête.

Tableau 9‑1 : Une convention communément adoptée pour la déclaration des valeurs p : dans de nombreuses publications, il est conventionnel de déclarer un de quatre résultats différents (par exemple, p < .05) comme indiqué ci-dessous. J’ai inclus la notation des « étoiles » (i.e., un * indique p < .05) parce que vous voyez parfois cette notation produite par un logiciel statistique. Il convient également de noter que certaines personnes écrivent ns. (non significatif) plutôt que p > .05.

Notation usuelle	Signif. étoiles	En langage courant	HO est….
\(p>.05\)	ns	Le test n’était pas significatif	Retenue
\(p<.05\)	*	Le test était significatif sur \(\alpha=.05\) mais pas sur \(\alpha=.01\) ou \(\alpha=.001\).	Rejetée
\(p<.01\)	**	Le test était significatif sur \(\alpha=.05\) et \(\alpha=.01\) mais pas sur \(\alpha=.001\).	Rejetée
\(p<.001\)	***	Le test était significatif à tous les niveaux	Rejetée

9.6.2 Deux solutions proposées

Dans la pratique, il est assez rare qu’un chercheur spécifie un seul niveau \(\alpha\) à l’avance. La convention veut plutôt que les scientifiques se fondent sur trois niveaux de signification standard : .05,.01 et.001. Lorsque vous rapportez vos résultats, vous indiquez lesquels (le cas échéant) de ces niveaux de signification vous permettent de rejeter l’hypothèse nulle. Ce point est résumé dans le Tableau 9‑1. Cela nous permet d’assouplir un peu la règle de décision, puisque \(p<.01\) implique que les données satisfont à une norme de preuve plus stricte que \(p<.05\) le ferait. Néanmoins, comme ces niveaux sont fixés à l’avance par convention, cela empêche les gens de choisir leur niveau \(\alpha\) après avoir examiné les données.

Néanmoins, un grand nombre de personnes préfèrent encore communiquer des valeurs p exactes. Pour beaucoup, l’avantage de permettre au lecteur de se faire sa propre opinion sur la façon d’interpréter p = .06 l’emporte sur les inconvénients éventuels. Dans la pratique, cependant, même parmi les chercheurs qui préfèrent des valeurs p exactes, il est assez courant d’écrire simplement p < .001 au lieu de rapporter une valeur exacte pour un petit p. C’est en partie parce que beaucoup de logiciels n’impriment pas réellement la valeur de p quand elle est si petite (par exemple, SPSS écrit simplement p = .000 chaque fois que p < .001), et en partie parce qu’une très petite valeur p peut être un peu trompeuse. L’esprit humain voit un nombre comme .00000000000001 et il est difficile de supprimer le sentiment instinctif que la preuve en faveur de l’hypothèse alternative est une quasi-certitude. Dans la pratique, cependant, ce n’est généralement pas le cas. La vie est une activité importante, désordonnée et compliquée, et tous les tests statistiques jamais inventés reposent sur des simplifications, des approximations et des hypothèses. Par conséquent, il n’est probablement pas raisonnable de s’éloigner d’une analyse statistique avec un sentiment de confiance plus fort que p < .001. En d’autres termes, p<.001 est vraiment un véritable indice de ce que sont “les preuves convaincantes pour le test concerné”.

À la lumière de tout cela, vous vous demandez peut-être ce que vous devriez faire exactement. Il y a pas mal de conseils contradictoires sur le sujet, certaines personnes soutenant que vous devriez déclarer la valeur exacte de p, et d’autres que vous devriez utiliser l’approche par paliers illustrée dans le Tableau 9‑1. Par conséquent, le meilleur conseil que je puisse donner est de vous suggérer de consulter les documents/rapports écrits dans votre domaine et de voir ce que semble être la convention. S’il ne semble pas y avoir de tendance constante, utilisez la méthode que vous préférez.

9.7 Exécuter le test d’hypothèse dans la pratique

Certains d’entre vous se demandent peut-être s’il s’agit d’un « vrai » test d’hypothèse, ou simplement d’un exemple de jeu que j’ai inventé. C’est réel. Dans la discussion précédente, j’ai construit le test à partir de principes de base, pensant que c’était le problème le plus simple que l’on puisse rencontrer dans la vie réelle. Cependant, ce test existe déjà. C’est ce qu’on appelle le test binomial, et il est implémenté dans Jamovi comme l’une des analyses statistiques disponibles lorsque vous cliquez sur le bouton « Frequencies ». Pour vérifier l’hypothèse nulle selon laquelle la probabilité de réponse est égale à la moitié de p = 0,5,⁶⁰ et en utilisant des données dans lesquelles x = 0,62 de n = 100 personnes ont donné la bonne réponse, disponible dans le fichier de données binomialtest.omv, nous obtenons les résultats présentés à la Figure 9‑4. <a name"f94>

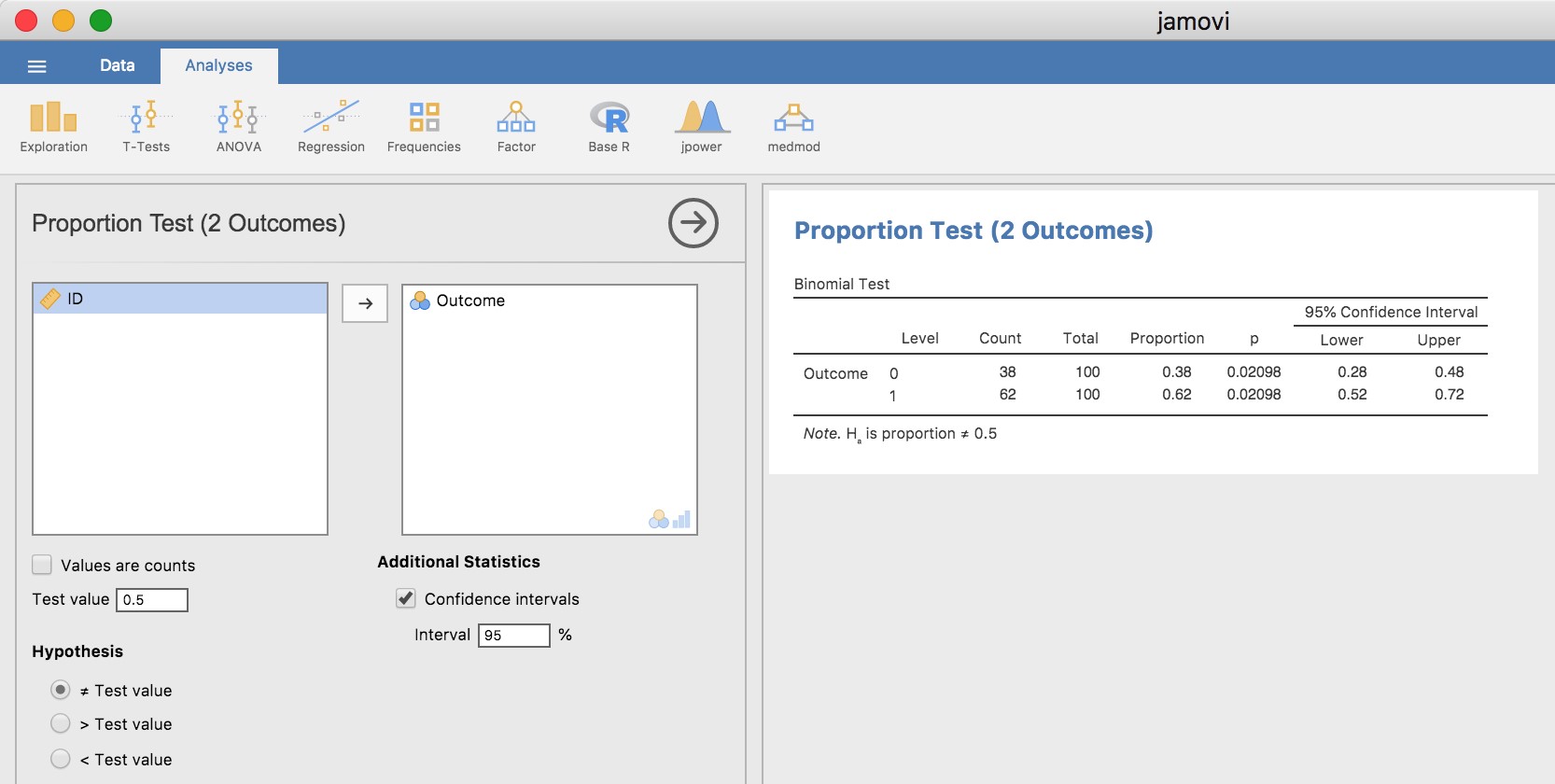
Figure 9‑4 : Analyse du test binomial et résultats dans Jamovi

Pour l’instant, cette sortie ne vous semble pas très familière, mais vous pouvez voir qu’elle vous donne plus ou moins les bons résultats. Plus précisément, la valeur p de 0,02 est inférieure au choix habituel de \(\alpha<.05\), vous pouvez donc rejeter l’hypothèse nulle. Nous parlerons beaucoup plus de la façon de lire ce genre de résultats au fur et à mesure, et après un certain temps, nous espérons que vous le trouverez assez facile à lire et à comprendre.

9.8 Taille de l’effet, taille de l’échantillon et puissance

Dans les sections précédentes, j’ai insisté sur le fait que le principal principe de conception qui sous-tend les tests d’hypothèses statistiques est que nous essayons de contrôler notre taux d’erreur de type I. Quand on fixe \(\alpha=.05\), nous essayons de nous assurer que seulement 5 % des hypothèses nulles réelles sont rejetées à tort. Cependant, cela ne signifie pas que nous ne nous soucions pas des erreurs de type II. En fait, du point de vue du chercheur, l’erreur de ne pas rejeter l’hypothèse nulle alors qu’elle est en fait fausse est extrêmement ennuyeuse. En gardant cela à l’esprit, un objectif secondaire des tests d’hypothèse est d’essayer de minimiser \(\beta\), le taux d’erreur de type II, bien que nous ne parlions généralement pas en termes de minimiser les erreurs de type II. Au lieu de cela, nous parlons de maximiser la puissance du test. Puisque la puissance est définie comme \(1-\beta\), c’est la même chose.

9.8.1 La fonction de puissance

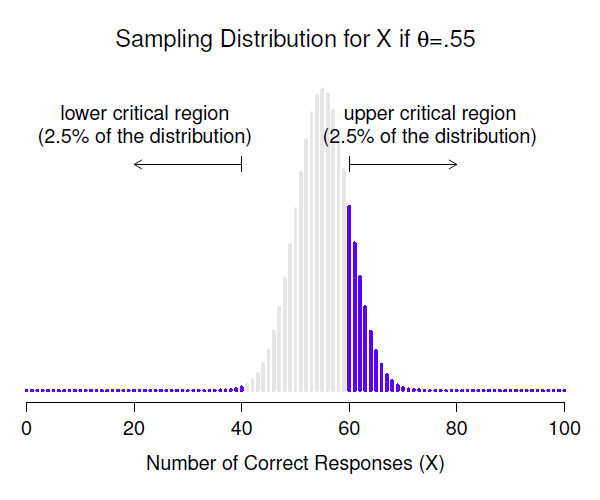
Figure 9‑5 : Distribution de l’échantillonnage sous l’hypothèse alternative pour une valeur de paramètre de population de \(\theta=0.55\). Une proportion raisonnable de la distribution se trouve dans la région de rejet.

Prenons un moment pour réfléchir à ce qu’est une erreur de type II. Une erreur de type II se produit lorsque l’hypothèse alternative est vraie, mais que nous ne sommes pas en mesure de rejeter l’hypothèse nulle. Idéalement, nous pourrions calculer un nombre unique \(\beta\) qui nous indique le taux d’erreur de type II, de la même manière que nous pouvons régler \(\alpha=.05\) pour le taux d’erreur de type I. Malheureusement, c’est beaucoup plus difficile à faire. Pour vous en rendre compte, notez que dans mon étude sur la PES l’hypothèse alternative correspond en fait à beaucoup de valeurs possibles de \(\theta\). En fait, l’hypothèse alternative correspond à toutes les valeurs de \(\theta\) à l’exception de 0,5. Supposons que la probabilité réelle que quelqu’un choisisse la bonne réponse est de 55 % (c.-à-d. \(\theta=0.55\)). Si c’est le cas, la distribution d’échantillonnage réelle pour X n’est pas la même que celle prévue par l’hypothèse nulle, car la valeur la plus probable pour X est maintenant de 55 sur 100. De plus, toute la distribution d’échantillonnage a maintenant changé, comme le montre la Figure 9‑5. Les régions critiques, bien sûr, ne changent pas. Par définition, les régions critiques sont basées sur ce que l’hypothèse nulle prédit. Ce que nous constatons dans cette figure, c’est que lorsque l’hypothèse nulle est fausse, une proportion beaucoup plus importante de la distribution d’échantillonnage se situe dans la région critique. Et bien sûr, c’est ce qui devrait arriver. La probabilité de rejeter l’hypothèse nulle est plus grande lorsque l’hypothèse nulle est fausse ! Cependant \(\theta=0.55\) n’est pas la seule possibilité compatible avec l’hypothèse alternative. Supposons plutôt que la valeur réelle de \(\theta\) est en fait 0.70. Qu’arrive-t-il à la distribution d’échantillonnage lorsque cela se produit ? La réponse, illustrée à la Figure 9‑6, est que la quasi-totalité de la distribution d’échantillonnage est maintenant passée dans la région critique. Par conséquent, si \(\theta=0.70\), la probabilité que nous rejetons correctement l’hypothèse nulle (c’est-à-dire la puissance du test) est beaucoup plus grande que si \(\theta=0.55\). Bref, alors que \(\theta=0.55\) et \(\theta=0.70\) font partie de l’hypothèse alternative, le taux d’erreur de type II est différent.

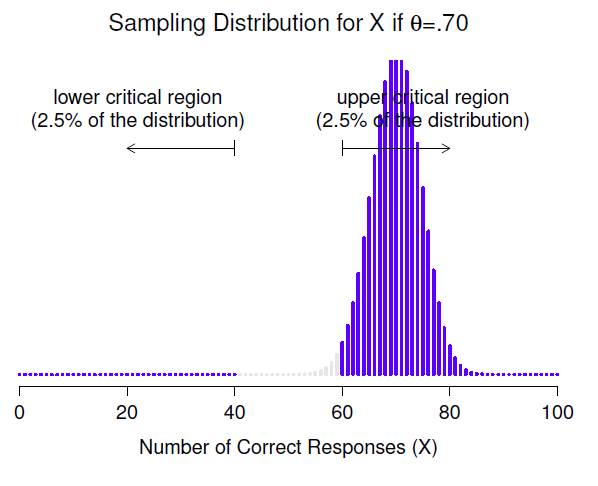
Figure 9‑6 : Distribution de l’échantillonnage sous l’hypothèse alternative pour une valeur de paramètre de population de \(\theta=.70\). Presque toute la distribution se trouve dans la région de rejet.

Tout cela signifie que la puissance d’un test (c.-à-d. \(1-\beta\)) dépend de la valeur réelle de \(\theta\). Pour illustrer cela, j’ai calculé la probabilité prévue de rejeter l’hypothèse nulle pour toutes les valeurs de \(\theta\), et je l’ai représentée à la Figure 9‑7. Ce graphique décrit ce que l’on appelle habituellement la fonction de puissance du test. C’est un bon résumé de la qualité du test, car il vous indique la puissance \((1-\beta)\) pour toutes les valeurs possibles de \(\theta\). Comme vous pouvez le constater, lorsque la valeur réelle de \(\theta\) est très élevée proche de 0,5, la puissance du test diminue très fortement, mais lorsqu’il est plus éloigné, la puissance est importante.

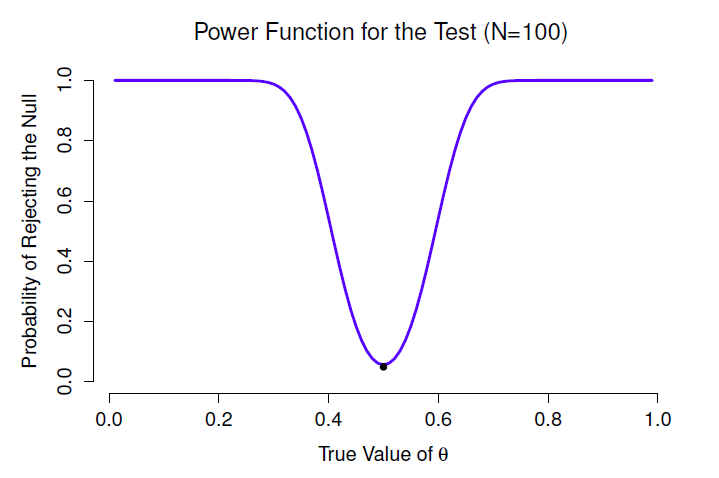
Figure 9‑7 : La probabilité que nous rejetterons l’hypothèse nulle, tracée en fonction de la valeur réelle de \(\theta\). Évidemment, le test est plus puissant (plus grande chance de rejet correct) si la valeur réelle de \(\theta\) est très différente de la valeur spécifiée dans l’hypothèse nulle (i.e. \(\theta=.5\)). Notez que lorsque \(\theta\) est en fait égal à .5 (représenté par un point noir), l’hypothèse nulle est en fait vraie et rejeter l’hypothèse nulle dans ce cas serait une erreur de type I.

9.8.2 Taille de l’effet

Puisque tous les modèles sont faux, le scientifique doit être attentif à ce qui est faux. Il est inapproprié de s’inquiéter des souris quand il y a des tigres à la maison. - George Box (Box, (1976), p. 792)

Le graphique de la Figure 9‑7 illustre un point assez élémentaire de la vérification des hypothèses. Si l’état réel du monde est très différent de ce que l’hypothèse nulle prédit, alors votre pouvoir sera très élevé, mais si l’état réel du monde est similaire à l’état nul (mais pas identique), la puissance du test sera très faible. Il est donc utile d’avoir un moyen de quantifier à quel point l’état réel du monde est « semblable » à l’hypothèse nulle. Une statistique qui le fait s’appelle une mesure de la taille de l’effet (p. ex. Cohen, (1988) ; Ellis, (2010)). La taille de l’effet est définie légèrement différemment selon les contextes (c’est pourquoi la présente section ne fait que parler en termes généraux), mais l’idée qualitative qu’elle tente de saisir est toujours la même. Quelle est l’ampleur de la différence entre les paramètres réels de la population et les valeurs des paramètres qui sont assumés par l’hypothèse nulle ? Dans notre exemple de la PES, si nous laissons \(\theta_{0}=0.5\) indiquer la valeur assumée par l’hypothèse nulle et laissons \(\theta\) indiquer la vraie valeur, alors une simple mesure de l’ampleur de l’effet pourrait être quelque chose comme la différence entre la vraie valeur et l’hypothèse nulle (c’est-à-dire \(\theta-\theta_{0}\)), ou peut-être simplement l’ampleur de cette différence, \(abs(\theta-\theta_{0})\)

Tableau 9‑2 : Un guide sommaire pour comprendre la relation entre la signification statistique et la valeur de l’effet. Fondamentalement, si vous n’avez pas de résultat significatif, l’ampleur de l’effet n’a pas beaucoup de sens parce que vous n’avez aucune preuve qu’il est même réel. D’un autre côté, si vous avez un effet significatif mais que votre taille d’effet est petite, il y a de fortes chances que votre résultat (bien que réel) ne soit pas très intéressant. Cependant, ce guide est très grossier. Cela dépend beaucoup de ce que vous étudiez exactement. Les petits effets peuvent être d’une importance pratique considérable dans certaines situations. Alors ne prenez pas cette table trop au sérieux. C’est un guide approximatif, au mieux.

	taille du grand effet	faible ampleur de l’effet
résultat significatif	la différence est réelle, et	la différence est réelle, mais
	d’importance pratique	pourrait ne pas être intéressant
résultat non significatif	aucun effet observé	aucun effet observé

Pourquoi calculer la taille de l’effet ? Supposons que vous avez mené votre expérience, recueilli les données et obtenu un effet significatif lorsque vous avez effectué votre test d’hypothèse. Ne suffit-il pas de dire que vous avez eu un effet significatif ? C’est le but des tests d’hypothèse, non ? Enfin, en quelque sorte. Oui, le but d’un test d’hypothèse est d’essayer de démontrer que l’hypothèse nulle est fausse, mais ce n’est pas la seule chose qui nous intéresse. Si l’hypothèse nulle affirmait que \(\theta=.5\) et nous montrons qu’elle n’est pas correcte, mais nous n’avons vraiment raconté que la moitié des choses. Rejeter l’hypothèse nulle implique que nous croyons que \(\theta\neq.5\), mais il y a une grande différence entre \(\theta=.51\) et \(\theta=.8\). Si nous trouvons que \(\theta=.8\), alors non seulement nous avons trouvé que l’hypothèse nulle est fausse, mais elle semble être très fausse. Par contre, supposons que nous ayons réussi à rejeter l’hypothèse nulle, mais il semble que la vraie valeur de \(\theta\) ne soit que de .51 (ce qui ne serait possible qu’avec une très grande étude). Bien sûr, l’hypothèse nulle est fausse, mais il n’est pas du tout sûr que nous ayons à nous en soucier parce que la taille de l’effet est si petite. Dans le contexte de mon étude sur la PES, nous pourrions encore nous en soucier puisque toute démonstration de vrais pouvoirs psychiques serait en fait plutôt cool⁶¹, mais dans d’autres contextes, une différence de 1% n’est généralement pas très intéressante, même si c’est une vraie différence. Supposons, par exemple, que nous examinions les différences dans les résultats aux examens du secondaire entre les garçons et les filles et qu’il s’avère que les résultats des filles sont en moyenne 1 % plus élevés que ceux des garçons. Si j’ai des données provenant de milliers d’étudiants, cette différence sera presque certainement statistiquement significative, mais peu importe à quel point la valeur p est faible, ce n’est pas très intéressant. Vous ne voudriez pas affirmer que l’éducation des garçons est en crise sur la base d’une si petite différence, n’est-ce pas ? C’est pour cette raison qu’il est de plus en plus courant (lentement, mais sûrement) de rapporter une mesure standard de la taille de l’effet avec les résultats du test d’hypothèse. Le test d’hypothèse lui-même vous dit si vous devez croire que l’effet que vous avez observé est réel (c.-à-d., pas seulement dû au hasard), alors que l’ampleur de l’effet vous dit si vous devez ou non vous y accorder de l’importance.

9.8.3 Augmenter la puissance de votre étude

Il n’est pas surprenant que les scientifiques soient assez obsédés par la maximisation de la puissance de leurs expériences. Nous voulons que nos expériences fonctionnent et nous voulons donc maximiser les chances de rejeter l’hypothèse nulle si elle est fausse (et bien sûr nous voulons généralement croire qu’elle est fausse !). Comme nous l’avons vu, l’un des facteurs qui influencent la puissance est la taille de l’effet. La première chose que vous pouvez faire pour augmenter votre puissance est donc d’augmenter la taille de l’effet. Dans la pratique, cela signifie que vous voulez concevoir votre étude de manière à ce que la taille de l’effet soit agrandie. Par exemple, dans mon étude sur la PES, je pourrais croire que les pouvoirs psychiques fonctionnent mieux dans une pièce calme et sombre avec moins de distractions pour perturber l’esprit. C’est pourquoi j’essaierais de mener mes expériences dans un tel environnement. Si je peux renforcer les capacités de PES des gens d’une manière ou d’une autre, alors la vraie valeur de \(\theta\) augmentera⁶² et donc ma taille d’effet sera plus grande. En bref, un design expérimental intelligent est un moyen d’augmenter la puissance, car il peut modifier la taille de l’effet.

Malheureusement, il arrive souvent que même avec les meilleures conceptions expérimentales, vous n’ayez qu’un effet minime. Peut-être, par exemple, l’ESP existe vraiment, mais même dans les meilleures conditions, elle est très très faible. Dans ces circonstances, le meilleur moyen d’augmenter la puissance est d’augmenter la taille de l’échantillon. En général, plus vous avez d’observations disponibles, plus il est probable que vous puissiez faire la distinction entre deux hypothèses. Si j’avais fait mon expérience sur la PES avec 10 participants et que 7 d’entre eux avaient deviné correctement la couleur de la carte cachée, vous ne seriez pas terriblement impressionné. Mais si je l’avais fait avec 10 000 participants, et que 7 000 d’entre eux avaient obtenu la bonne réponse, vous auriez beaucoup plus tendance à penser que j’avais découvert quelque chose. En d’autres termes, la puissance augmente avec la taille de l’échantillon. Ceci est illustré dans la Figure 9‑8, qui montre la puissance du test pour un paramètre vrai de \(\theta=0.7\) pour toutes les tailles d’échantillon N de 1 à 100, où je suppose que l’hypothèse nulle prédit que \(\theta_{0}=0.5\).

Parce que la puissance est importante, chaque fois que vous envisagez de faire une expérience, il serait très utile de savoir quel niveau de puissance vous êtes susceptible d’avoir. Il n’est jamais possible d’en être sûr car il est impossible de connaître la taille réelle de votre effet. Cependant, il est souvent (enfin, parfois) possible de deviner sa taille. Si oui, vous pouvez deviner la taille de l’échantillon dont vous avez besoin ! Cette idée s’appelle l’analyse de puissance, et si c’est faisable, alors c’est très utile. Il peut vous dire si vous avez assez de temps ou d’argent pour mener à bien l’expérience. Il est de plus en plus courant de voir des gens affirmer que l’analyse de puissance devrait faire partie intégrante de la conception expérimentale, alors cela vaut la peine d’en savoir plus. Je ne parle pas de l’analyse de puissance dans ce livre, cependant. C’est en partie pour une raison ennuyeuse et en partie pour une raison de fond. La raison ennuyeuse est que je n’ai pas encore eu le temps d’écrire sur l’analyse de puissance. Le plus important, c’est que je me méfie encore un peu de l’analyse de puissance. En tant que chercheur, je me suis très rarement trouvé en mesure de le faire. Soit (a) mon expérience est une expérience un peu non standard et je ne sais pas comment définir correctement la taille de l’effet, ou (b) j’ai littéralement si peu d’idée sur la taille de l’effet que je ne saurais pas comment interpréter les réponses.

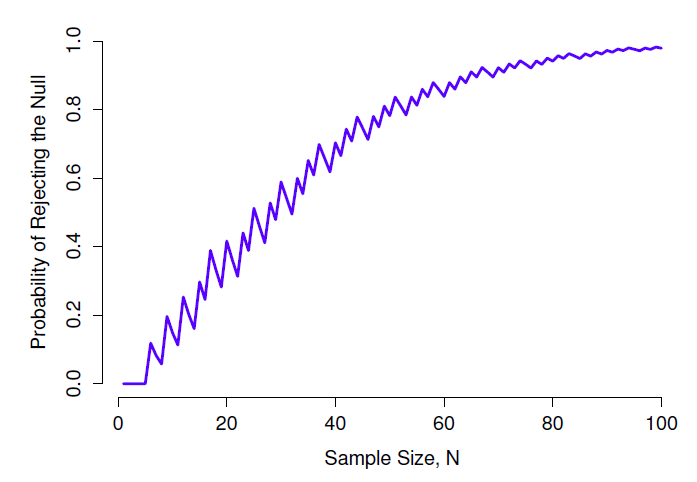
Figure 9‑8 : La puissance de notre test tracée en fonction de la taille de l’échantillon N. Dans ce cas, la valeur réelle de \(\theta\) est 0,7 mais l’hypothèse nulle est que \(\theta=0,5\). Dans l’ensemble, plus N est grand, plus la puissance est grande. (Les petits zig-zags dans cette fonction se produisent à cause de quelques interactions étranges entre \(theta\), \(\alpha\) et le fait que la distribution binomiale est discrète, cela ne pose pas de problème pour notre propos).

En plus de cela, après de longues conversations avec quelqu’un qui est consultant en statistiques pour gagner sa vie (ma femme, en l’occurrence), je ne peux m’empêcher de remarquer qu’en pratique, le seul moment où quelqu’un lui demande de faire une analyse de puissance c’est quand elle aide quelqu’un à rédiger une demande de subvention. En d’autres termes, le seul moment où un scientifique semble vouloir une analyse de puissance dans la vraie vie, c’est lorsqu’il est forcé de le faire par un processus bureaucratique. Ça ne fait partie du travail quotidien de personne. Bref, j’ai toujours été d’avis que même si la puissance est un concept important, l’analyse de puissance n’est pas aussi utile que les gens le disent, sauf dans les rares cas où (a) quelqu’un a trouvé comment calculer la puissance pour votre plan expérimental réel et (b) vous avez une assez bonne idée de la taille de l’effet probable.⁶³ Peut-être que d’autres personnes ont eu de meilleures expériences que moi, mais personnellement je n’ai jamais été dans une situation où les deux (a) et (b) étaient vrais. Peut-être que je serai convaincu du contraire à l’avenir, et probablement qu’une prochaine version de ce livre inclurait une discussion plus détaillée de l’analyse de puissance, mais pour l’instant, c’est à peu près tout ce que je suis capable de dire sur le sujet.

9.9 Quelques points à prendre en considération

Ce que je vous ai décrit dans ce chapitre est le cadre orthodoxe du test de signification des hypothèses nulles (Null hypothesis significance testing : NHST). Comprendre le fonctionnement des NHST est une nécessité absolue parce qu’il s’agit de l’approche dominante en matière de statistiques inférentielles depuis qu’elles ont pris de l’importance au début du XXe siècle. C’est ce sur quoi la grande majorité des scientifiques se fient pour l’analyse de leurs données, donc même si vous détestez cela, vous devez le savoir. Cependant, l’approche n’est pas sans problèmes. Ce cadre a un certain nombre de bizarreries, des bizarreries historiques sur la façon dont il a vu le jour, des différends théoriques sur le bien-fondé du cadre et de nombreux pièges pratiques pour ceux qui ne sont pas prudents. Je ne vais pas entrer dans les détails à ce sujet, mais je pense qu’il vaut la peine d’aborder brièvement quelques-unes de ces questions.

9.9.1 Neyman contre Fisher

La première chose que vous devez savoir, c’est que la NHST orthodoxe est en fait une synthèse de deux approches assez différentes de la vérification des hypothèses, l’une proposée par Sir Ronald Fisher et l’autre par Jerzy Neyman (voir Lehmann (2011), pour un résumé historique). L’histoire est confuse parce que Fisher et Neyman étaient de vraies personnes dont les opinions ont changé au fil du temps, et à aucun moment ils n’ont offert « la publication définitive » sur la façon dont nous devrions interpréter leur travail plusieurs décennies plus tard. Cela dit, voici un bref résumé de ce que je pense de ces deux approches.

Parlons d’abord de l’approche de Fisher. Pour autant que je sache, Fisher a supposé que vous n’aviez qu’une seule hypothèse (l’hypothèse nulle) et que ce que vous voulez faire est de découvrir si l’hypothèse nulle est incompatible avec les données. De son point de vue, ce qu’il faut faire, c’est vérifier si les données sont « suffisamment improbables » selon l’hypothèse nulle. En fait, si vous vous souvenez de ce que nous avons dit plus tôt, c’est ainsi que Fisher définit la valeur p. Selon Fisher, si l’hypothèse nulle fournissait un très mauvais résumé des données, vous pourriez la rejeter en toute sécurité. Mais, comme vous n’avez pas d’autres hypothèses pour la comparer, il n’y a aucun moyen « d’accepter l’alternative » parce que vous n’avez pas nécessairement une alternative explicitement énoncée. C’est plus ou moins tout ce qu’il y a à faire.

En revanche, Neyman pensait que la vérification des hypothèses servait de guide d’action et que son approche était un peu plus formelle que celle de Fisher. Selon lui, il y a plusieurs choses que vous pourriez faire (accepter l’hypothèse nulle ou accepter l’alternative) et le but du test était de vous dire laquelle est supportées par les données. De ce point de vue, il est essentiel de bien préciser votre hypothèse alternative. Si vous ne connaissez pas l’hypothèse alternative, alors vous ne savez pas quelle est la puissance du test, ni même quelle action a du sens. Son cadre exige véritablement une concurrence entre les différentes hypothèses. Pour Neyman, la valeur p ne mesurait pas directement la probabilité des données (ou des données plus extrêmes) sous l’hypothèse nulle, il s’agissait plutôt d’une description abstraite au sujet de laquelle les « tests possibles » vous disaient d’accepter l’hypothèse nulle ou d’accepter l’alternative.

Comme vous pouvez le constater, ce que nous avons aujourd’hui est un étrange méli-mélo des deux. Nous parlons d’avoir à la fois une hypothèse nulle et une hypothèse alternative (Neyman), mais nous définissons généralement⁶⁴ la valeur p en termes de données extrêmes (Fisher), alors nous avons toujours des valeurs \(\alpha\) (Neyman). Certains des tests statistiques ont explicitement spécifié des alternatives (Neyman) mais d’autres sont assez vagues à ce sujet (Fisher). Et, selon certains au moins, nous n’avons pas le droit de parler d’accepter l’alternative (Fisher). C’est le bazar, mais j’espère au moins que ça explique pourquoi c’est le bazar.

9.9.2 Bayésiens contre fréquentistes

Plus tôt dans ce chapitre, j’ai insisté sur le fait qu’on ne peut pas interpréter la valeur p comme la probabilité que l’hypothèse nulle soit vraie. Le NHST est fondamentalement un outil fréquentiste (voir chapitre 7) et ne permet donc pas d’attribuer des probabilités aux hypothèses. L’hypothèse nulle est soit vraie, soit fausse. L’approche bayésienne des statistiques interprète la probabilité comme un degré de croyance, alors il est tout à fait normal de dire qu’il y a une probabilité de 10 % que l’hypothèse nulle soit vraie. Ce n’est qu’un reflet du degré de confiance que vous avez dans cette hypothèse. Vous n’êtes pas autorisé à le faire dans le cadre de l’approche fréquentiste. Rappelez-vous que si vous êtes un fréquentiste, une probabilité ne peut être définie qu’en fonction de ce qui se produit après un grand nombre de répétitions indépendantes (c.-à-d., une fréquence à long terme). Si c’est votre interprétation de la probabilité, parler de la « probabilité » que l’hypothèse nulle soit vraie est un charabia complet : une hypothèse nulle est soit vraie, soit fausse. Vous ne pouvez pas parler d’une fréquence à long terme pour cette affirmation. Parler de « la probabilité de l’hypothèse nulle » n’a pas plus de sens que de « la couleur de la liberté ».

Plus important encore, il ne s’agit pas d’une question purement idéologique. Si vous décidez que vous êtes Bayésien et que vous êtes d’accord pour faire des déclarations de probabilité au sujet des hypothèses, vous devez suivre les règles bayésiennes pour calculer ces probabilités. J’en parlerai plus en détail au chapitre 15, mais pour l’instant, ce que je tiens à vous faire remarquer, c’est que la valeur p est une terrible approximation de la probabilité que H0 soit vrai. Si ce que vous voulez savoir est la probabilité de l’hypothèse nulle, alors la valeur p n’est pas celle que vous recherchez !

9.9.3 Pièges

Comme vous pouvez le constater, la théorie qui sous-tend les tests d’hypothèse est un fouillis, et même maintenant il y a des controverses dans les statistiques sur la façon dont cela devrait fonctionner. Cependant, les désaccords entre statisticiens ne sont pas notre véritable préoccupation ici. Notre véritable préoccupation est l’analyse pratique des données. Et bien que l’approche « orthodoxe » de la vérification de l’importance des hypothèses nulles présente de nombreux inconvénients, même un Bayésien non repentant comme moi sera d’accord pour dire qu’elles peuvent être utiles si elles sont utilisées de façon responsable. La plupart du temps, ils donnent des réponses sensées et vous pouvez les utiliser pour apprendre des choses intéressantes. Mis à part les différentes idéologies et les confusions historiques dont nous avons parlé, il n’en demeure pas moins que le plus grand danger dans toutes les statistiques est l’usage irréfléchi. Je ne parle pas de stupidité, je parle littéralement d’insouciance. La hâte d’interpréter un résultat sans prendre le temps de réfléchir à ce que chaque test dit réellement au sujet des données, et de vérifier si cela correspond à la façon dont vous l’avez interprété. C’est là que se trouve le plus grand piège.

Pour en donner un exemple, prenons la situation suivante (voir Gelman et Stern (2006)). Supposons que je mène mon étude sur la PES et que j’ai décidé d’analyser les données séparément pour les participants et les participantes. Parmi les participants, 33 sur 50 ont deviné la couleur de la carte correctement. C’est un effet significatif (p = .03). Parmi les participantes, 29 sur 50 ont deviné correctement. Ce n’est pas un effet significatif (p = .32). En observant cela, il est extrêmement tentant pour les gens de commencer à se demander pourquoi il y a une différence entre les hommes et les femmes du point de vue de leurs capacités psychiques. Cependant, c’est une erreur. Si vous y réfléchissez bien, nous n’avons pas fait un test qui compare explicitement les hommes et les femmes. Tout ce que nous avons fait est de comparer les hommes au hasard (le test binomial était significatif) et les femmes au hasard (le test binomial était non significatif). Si nous voulons argumenter qu’il y a une différence réelle entre les hommes et les femmes, nous devrions probablement tester l’hypothèse nulle qu’il n’y a pas de différence ! Nous pouvons le faire en utilisant un test d’hypothèse différent,⁶⁵ mais lorsque nous le faisons, il s’avère que nous n’avons aucune preuve que les hommes et les femmes sont significativement différents (p = .54). Pensez-vous qu’il y a quelque chose de fondamentalement différent entre les deux groupes ? Bien sûr que non. Ce qui s’est passé ici, c’est que les données des deux groupes (hommes et femmes) sont assez limitées. Par pur hasard, l’un d’eux s’est retrouvé du côté magique du p = .05, et l’autre ne l’a pas fait. Cela ne veut pas dire que les hommes et les femmes sont différents. Cette erreur est si courante qu’il faut toujours s’en méfier. La différence entre significatif et non significatif n’est pas la preuve d’une différence réelle. Si vous voulez dire qu’il y a une différence entre deux groupes, alors vous devez tester cette différence !

L’exemple ci-dessus n’est qu’un exemple. Je l’ai choisi parce qu’il s’agit d’un problème courant, mais, dans l’ensemble, l’analyse des données peut être difficile à faire correctement. Pensez à ce que vous voulez tester, pourquoi vous voulez le tester, et si oui ou non les réponses que vous voulez tester pourraient avoir un sens dans le monde réel.

9.10 Résumé

La vérification des hypothèses nulles est l’un des éléments les plus omniprésents de la théorie statistique. La grande majorité des articles scientifiques rapportent les résultats d’un test d’hypothèse ou d’un autre. En conséquence, il est presque impossible de s’en sortir en science sans avoir au moins une compréhension superficielle de ce que signifie une valeur p, ce qui en fait l’un des chapitres les plus importants de l’ouvrage. Comme d’habitude, je terminerai le chapitre par un bref résumé des idées clés dont nous avons parlé :

• Hypothèses de recherche et hypothèses statistiques. Hypothèses nulles et alternatives. (Section 9.1).
• Erreurs de type 1 et de type 2 (section 9.2)
• Statistiques des tests et distributions d’échantillonnage (Section 9.3)
• Les tests d’hypothèse en tant que processus décisionnel (Section 9.4)
• p comme décisions « douces « (Section 9.5)
• Rédaction des résultats d’un test d’hypothèse (section 9.6)
• Exécution du test d’hypothèse dans la pratique (Section 9.7)
• Ampleur et puissance de l’effet (Section 9.8)
• Quelques questions à prendre en considération concernant la vérification des hypothèses (Section 9.9)

Plus loin dans le livre, au chapitre 16, je reviendrai sur la théorie des tests d’hypothèse nulle d’un point de vue bayésien et présenterai un certain nombre de nouveaux outils que vous pouvez utiliser si vous n’aimez pas particulièrement l’approche orthodoxe. Mais pour l’instant, nous en avons terminé avec la théorie statistique abstraite, et nous pouvons commencer à discuter d’outils spécifiques d’analyse des données.

References

Box, George E. P. 1976. “Science and Statistics.” Journal of the American Statistical Association 71 (356): 791–99. https://doi.org/10.1080/01621459.1976.10480949.

Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Hillsdale, N.J: L. Erlbaum Associates.

Ellis, Paul D. 2010. The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge University Press.

Gelman, Andrew, and Hal Stern. 2006. “The Difference Between ‘Significant’ and ‘Not Significant’ Is Not Itself Statistically Significant.” The American Statistician 60 (4): 328–31. https://doi.org/10.1198/000313006X152649.

Lehmann, Erich L. 2011. Fisher, Neyman, and the Creation of Classical Statistics. New York: Springer-Verlag. https://doi.org/10.1007/978-1-4419-9500-1.

---

52. La citation provient du texte de Wittgenstein (1922), Tractatus Logico-Philosphicus.↩︎

53. Une note technique. La description ci-dessous diffère subtilement de la description standard donnée dans un grand nombre de textes d’introduction. La théorie orthodoxe de la vérification des hypothèses nulles a émergé des travaux de Sir Ronald Fisher et Jerzy Neyman au début du 20e siècle ; mais Fisher et Neyman avaient en fait des points de vue très différents sur la façon dont elle devrait fonctionner. Le traitement standard des tests d’hypothèse que la plupart des textes utilisent est un hybride des deux approches. Le traitement est ici un peu plus proche de celui de Neyman que de l’orthodoxie, surtout en ce qui concerne la signification de la valeur p.↩︎

54. Je présente mes excuses à tous ceux qui croient vraiment à ce genre de choses, mais d’après ce que j’ai lu dans la documentation sur la PES, il n’est tout simplement pas raisonnable de penser que c’est réel. Pour être juste, cependant, certaines des études sont rigoureusement conçues, alors c’est en fait un domaine intéressant pour réfléchir à la conception de la recherche en psychologie. Et bien sûr, notre pays est assez libre pour que vous puissiez passer votre temps et vos efforts à me prouver que j’ai tort si vous le souhaitez, mais je ne pense pas que ce soit une utilisation terriblement pragmatique de votre intellect.↩︎

55. Cette analogie ne fonctionne que si vous êtes issu d’un système juridique accusatoire comme celui du Royaume-Uni, des États-Unis et de l’Australie. D’après ce que j’ai compris, le système inquisitoire français est très différent.↩︎

56. Un aparté concernant le langage que vous utilisez pour parler de vérification d’hypothèses. Tout d’abord, un terme que vous devriez vraiment éviter, c’est le mot « prouver ». Un test statistique ne prouve pas vraiment qu’une hypothèse est vraie ou fausse. La preuve implique la certitude et, comme le dit l’adage, les statistiques signifient qu’il n’est jamais nécessaire de dire que l’on est certain. Sur ce point, presque tout le monde sera d’accord. Cependant, au-delà de cela, il y a beaucoup de confusion. Certains prétendent que vous n’avez le droit de faire que des affirmations comme « rejeter l’hypothèse nulle », « omettre de rejeter la l’hypothèse nulle », ou peut-être « retenir l’hypothèse nulle ». Selon ce point de vue, on ne peut pas dire des choses comme « accepter l’hypothèse alternative » ou « accepter l’hypothèse nulle ». Personnellement, je pense que c’est trop sévère. À mon avis, cela confond la mise à l’épreuve d’hypothèses nulles avec la vision falsifiante du processus scientifique de Karl Popper. Bien qu’il y ait des similitudes entre la falsification et la vérification d’hypothèses nulles, elles ne sont pas équivalentes. Cependant, bien que je pense personnellement que c’est bien de parler d’accepter une hypothèse (à condition que « l’acceptation » ne signifie pas nécessairement que c’est vrai, surtout dans le cas de l’hypothèse nulle), beaucoup de gens ne seront pas d’accord. Surtout gardez à l’esprit que cette bizarrerie particulière existe pour ne pas être pris au dépourvu lors de la rédaction de vos propres résultats.↩︎

57. Strictement parlant, le test que je viens de construire a \(\alpha=.057\), ce qui est un peu trop généreux. Cependant, si j’avais choisi 39 et 61 comme limites pour la région critique, alors la région critique ne couvre que 3,5 % de la distribution. Je me suis dit qu’il était plus logique d’utiliser 40 et 60 comme valeurs critiques et d’être prêt à tolérer un taux d’erreur de type I de 5,7%, puisque c’est le plus près possible d’une valeur de \(\alpha=0.5\).↩︎

58. Internet semble assez convaincu qu’Ashley a dit cela, bien que je n’arrive pas à trouver quelqu’un prêt à donner une source pour cette affirmation↩︎

59. C’est p " . 00000000000000000000000000000000136 pour ceux qui n’aiment pas la notation scientifique !↩︎

60. Notez que le p ici n’a rien à voir avec une valeur p. L’argument p du test binomial de Jamovi correspond à la probabilité d’obtenir une réponse correcte, selon l’hypothèse nulle. En d’autres termes, c’est la valeur \(\theta\).↩︎

61. Bien qu’en pratique, une très petite taille de l’effet soit inquiétante parce que même des défauts méthodologiques mineurs peuvent être responsables de l’effet, et qu’en pratique aucune expérience n’est parfaite, il y a toujours des problèmes méthodologiques à prendre en compte.↩︎

62. Notez que le vrai paramètre de population \(\theta\) ne correspond pas nécessairement à un fait immuable de la nature. Dans ce contexte, \(\theta\) n’est que la véritable probabilité que les gens devinent correctement la couleur de la carte dans l’autre pièce. En tant que tel, le paramètre de population peut être influencé par toutes sortes de choses. Bien sûr, tout ceci est basé sur l’hypothèse que la PES existe réellement !↩︎

63. Les chercheurs qui étudient l’efficacité d’un nouveau traitement médical et qui précisent à l’avance l’importance de l’effet à détecter, par exemple en plus de tout traitement existant, peuvent faire exception à cette règle. De cette façon, il est possible d’obtenir des informations sur la valeur potentielle d’un nouveau traitement.↩︎

64. Bien que ce livre décrive à la fois la définition de Neyman et de Fisher de la valeur p, la plupart ne le font pas. La plupart des manuels d’introduction ne vous donneront que la version Fisher.↩︎

65. Dans ce cas, le test du chi carré de Pearson sur l’indépendance (chapitre 10)↩︎