Chapitre 8 Estimation de quantités inconnues à partir d’un échantillon
Au début du dernier chapitre, j’ai souligné la distinction cruciale entre statistiques descriptives et statistiques inférentielles. Comme nous l’avons vu au chapitre 4, le rôle des statistiques descriptives est de résumer de façon concise ce que nous savons. En revanche, le but des statistiques inférentielles est « d’apprendre ce que nous ne savons pas de ce que nous faisons ». Maintenant que nous avons une base en théorie des probabilités, nous sommes bien placés pour réfléchir au problème de l’inférence statistique. Quels genres de choses aimerions-nous apprendre ? Et comment les apprend-on ? Telles sont les questions qui sont au cœur des statistiques inférentielles, et elles sont traditionnellement divisées en deux « grandes idées » : l’estimation et la vérification d’hypothèses. Le but de ce chapitre est de présenter la première de ces grandes idées, la théorie de l’estimation, mais je vais d’abord parler de la théorie de l’échantillonnage parce que la théorie de l’estimation n’a de sens que si vous comprenez l’échantillonnage. Par conséquent, le présent chapitre se divise naturellement en deux parties : les sections 8.1 à 8.3 sont axées sur la théorie de l’échantillonnage, et les sections 8.4 et 8.5 utilisent la théorie de l’échantillonnage pour discuter de la façon dont les statisticiens envisagent l’estimation.
8.1 Échantillons, populations et échantillonnage
Dans le préambule de la quatrième partie, j’ai parlé de l’énigme de l’insertion et j’ai souligné le fait que tout apprentissage exige que l’on fasse des hypothèses. Accepter que c’est vrai, c’est notre première tâche que de formuler des hypothèses assez générales sur des données qui ont du sens. C’est là qu’intervient la théorie de l’échantillonnage. Si la théorie des probabilités est le fondement de toute théorie statistique, la théorie de l’échantillonnage est le cadre autour duquel vous pouvez construire le reste de la maison. La théorie de l’échantillonnage joue un rôle énorme en précisant les hypothèses sur lesquelles reposent vos inférences statistiques. Pour parler de la façon dont les statisticiens perçoivent les inférences, nous devons être un peu plus explicites sur ce dont nous tirons des inférences (l’échantillon) et sur ce à propos de quoi nous tirons des inférences (la population).
Dans presque toutes les situations qui nous intéressent, les données dont nous disposons en tant que chercheurs sont un échantillon de données. Nous avons peut-être fait des expériences avec un certain nombre de participants, une société de sondage a peut-être téléphoné à un certain nombre de personnes pour leur poser des questions sur leurs intentions de vote, et ainsi de suite. De cette façon, l’ensemble des données dont nous disposons est fini et incomplet. Par exemple, une société de sondage n’a ni le temps ni l’argent nécessaires pour sonder tous les électeurs du pays. Dans notre discussion précédente sur les statistiques descriptives (chapitre 4), cet échantillon était la seule chose qui nous intéressait. Notre seul but était de trouver des moyens de décrire, de résumer et de représenter graphiquement cet échantillon. Cela est sur le point de changer.
8.1.1 Définir une population
Un échantillon est une chose concrète. Vous pouvez ouvrir un fichier de données et il y a les données de votre échantillon. Une population, par contre, est une idée plus abstraite. Il s’agit de l’ensemble de toutes les personnes possibles, ou de toutes les observations possibles, au sujet desquelles vous voulez tirer des conclusions et qui est généralement beaucoup plus grand que l’échantillon. Dans un monde idéal, le chercheur commencerait l’étude avec une idée claire de ce qu’est la population d’intérêt, puisque le processus de conception d’une étude et de vérification des hypothèses avec les données dépend de la population au sujet de laquelle vous voulez faire des affirmations.
Parfois, il est facile d’indiquer la population d’intérêt. Par exemple, dans l’exemple de la « société de sondage » qui a ouvert le chapitre, la population se composait de tous les électeurs inscrits au moment de l’étude, des millions de personnes. L’échantillon était constitué d’un ensemble de 1000 personnes qui appartiennent toutes à cette population. Dans la plupart des études, la situation est beaucoup moins simple. Dans une expérience psychologique typique, déterminer la population d’intérêt est un peu plus compliqué. Supposons que je mène une expérience à laquelle participent 100 étudiants de premier cycle. Mon but, en tant que cognitiviste, est d’essayer d’apprendre quelque chose sur le fonctionnement de l’esprit. De ce point de vue, lequel des éléments suivants correspondrait à la « population » :
- Tous les étudiants en psychologie de l’Université d’Adélaïde ?
- Les étudiants en psychologie de premier cycle en général, n’importe où dans le monde ?
- Des Australiens vivent actuellement ?
- Des Australiens du même âge que mon échantillon ?
- Quelqu’un de vivant ?
- Un être humain, passé, présent ou futur ?
- Tout organisme biologique ayant un degré d’intelligence suffisant et opérant dans un environnement terrestre ?
- Un être intelligent ?
Chacune de ces définitions définit un véritable groupe d’entités possédant un esprit, qui pourraient toutes m’intéresser en tant que cognitiviste, et savoir quelle devrait être la véritable population d’intérêt n’est pas du tout clair. Prenons un autre exemple, celui du jeu Wellesley-Croker dont nous avons discuté dans l’introduction. L’échantillon ici est une séquence spécifique de 12 victoires et 0 défaite pour Wellesley. Quelle est la population ?
- Tous les résultats jusqu’à ce que Wellesley et Croker arrivent à destination ?
- Tous les résultats si Wellesley et Croker avaient joué le jeu pour le reste de leur vie ?
- Tous les résultats si Wellseley et Croker vivaient éternellement et jouaient le jeu jusqu’à ce que le monde soit à court de collines ?
- Tous les résultats si nous créions un ensemble infini d’univers parallèles et que la paire Wellesely/Croker faisait des suppositions sur les 12 mêmes collines dans chaque univers ?
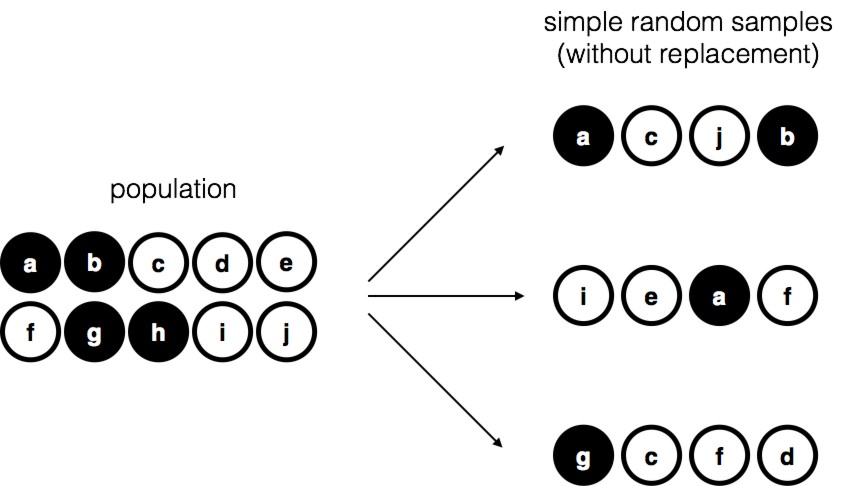
Figure 8‑1 : Échantillonnage aléatoire simple sans remplacement à partir d’une population finie
Encore une fois, ce n’est pas évident de savoir quelle est la population.
8.1.2 Échantillons aléatoires simples
Quelle que soit ma définition de la population, le point critique est que l’échantillon est un sous-ensemble de la population et que notre but est d’utiliser notre connaissance de l’échantillon pour tirer des conclusions sur les propriétés de la population. La relation entre les deux dépend de la procédure de sélection de l’échantillon. Cette procédure est appelée méthode d’échantillonnage et il est important de comprendre pourquoi elle est importante.
Pour simplifier les choses, imaginons que nous ayons un sac contenant 10 jetons. Chaque jeton a une lettre unique imprimée sur lui afin que nous puissions distinguer les 10 jetons. Les jetons sont disponibles en deux couleurs, noir et blanc. Cet ensemble de jetons est la population d’intérêt et il est représenté graphiquement à gauche de la Figure 8‑1. Comme vous pouvez le voir en regardant l’image, il y a 4 jetons noirs et 6 jetons blancs, mais bien sûr dans la vraie vie nous ne le saurions pas si nous ne regardons pas dans le sac. Imaginez maintenant que vous faites « l’expérience » suivante : vous secouez le sac, fermez les yeux et retirez 4 jetons sans en remettre aucune dans le sac. D’abord le jeton a (noire), puis le jeton c (blanche), puis j (blanche) et enfin b (noire). Si vous le souhaitez, vous pouvez ensuite remettre toutes les jetons dans le sac et répéter l’expérience, comme illustré à droite sur la Figure 8‑1. Chaque fois que vous obtenez des résultats différents, mais la procédure est identique dans chaque cas. Le fait qu’une même procédure peut conduire à des résultats différents à chaque fois nous conduits à parler d’un processus aléatoire.44 Cependant, parce que nous avons secoué le sac avant de retirer les jetons, il semble raisonnable de penser que chaque jeton a les mêmes chances d’être sélectionnée. Une procédure dans laquelle chaque membre de la population a les mêmes chances d’être sélectionné s’appelle un simple échantillon aléatoire. Le fait que nous n’ayons pas remis les jetons dans le sac après les avoir retirées signifie que vous ne pouvez pas observer la même chose deux fois, et dans de tels cas les observations sont les suivantes dont on dit qu’ils ont été échantillonnés sans remise.
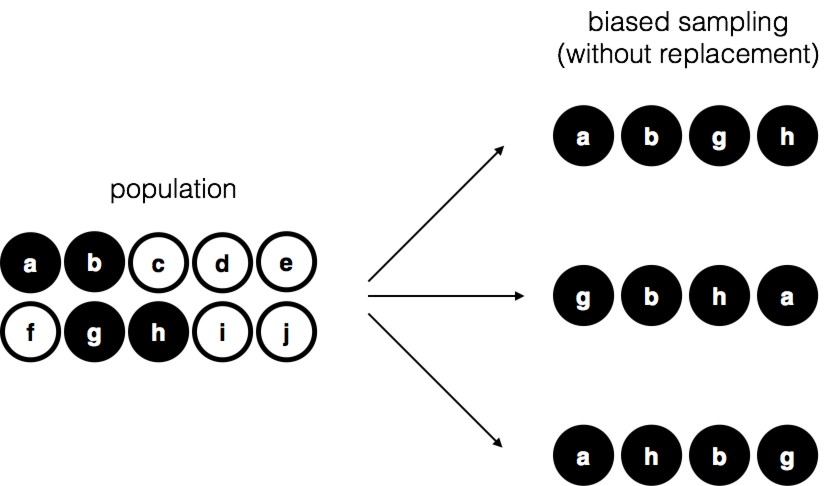
Figure 8‑2 : Échantillonnage biaisé sans remplacement à partir d’une population finie
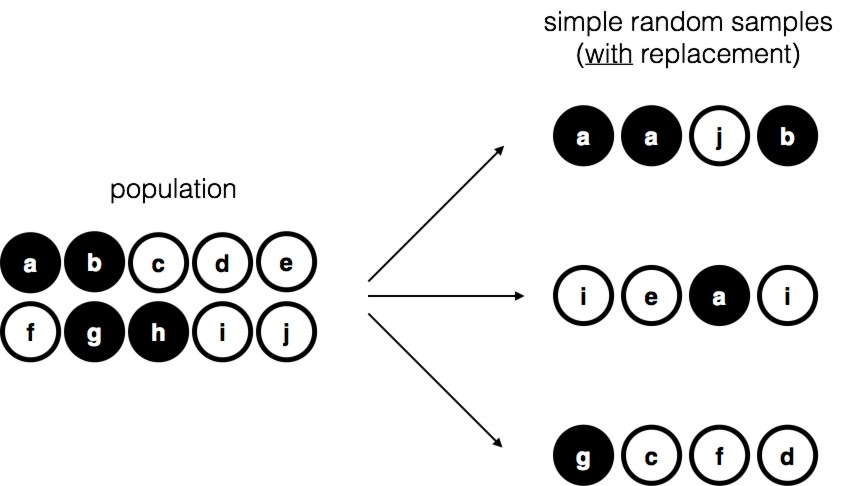
Figure 8‑3 : Échantillonnage aléatoire simple avec remplacement dans une population finie
Pour vous assurer de bien comprendre l’importance de la procédure d’échantillonnage, envisagez une autre façon de procéder à l’expérience. Supposons que mon fils de 5 ans ait ouvert le sac et décidé de retirer quatre jetons noirs sans en remettre aucun dans le sac. Ce plan d’échantillonnage biaisé est illustré à la Figure 8‑2. Considérons maintenant la valeur probante de voir 4 jetons noirs et 0 jetons blancs. Cela dépend clairement du plan d’échantillonnage. Si vous savez que le plan d’échantillonnage est biaisé pour ne sélectionner que des jetons noirs, alors un échantillon composé uniquement de jetons noirs ne vous dit pas grand-chose sur la population ! C’est la raison pour laquelle les statisticiens aiment beaucoup qu’un ensemble de données puisse être considéré comme un simple échantillon aléatoire, parce qu’il rend l’analyse des données beaucoup plus facile.
Une troisième procédure mérite d’être mentionnée. Cette fois-ci, nous fermons les yeux, secouons le sac et sortons un jeton. Cette fois, cependant, nous enregistrons l’observation et remettons le jeton dans le sac. Encore une fois, nous fermons les yeux, secouons le sac et sortons un jeton. Nous répétons ensuite cette procédure jusqu’à ce que nous ayons 4 jetons. Les ensembles de données générés de cette façon sont encore de simples échantillons aléatoires, mais parce que nous remettons les jetons dans le sac immédiatement après les avoir tirés, on parle d’un échantillon avec remise. La différence entre cette situation et la première est qu’il est possible d’observer le même membre de la population plusieurs fois, comme l’illustre la Figure 8‑3.
D’après mon expérience, la plupart des expériences de psychologie ont tendance à être des échantillonnages sans remise, parce que la même personne n’est pas autorisée à participer deux fois à l’expérience. Toutefois, la plupart des théories statistiques reposent sur l’hypothèse que les données proviennent d’un simple échantillon aléatoire avec remise. Dans la vie réelle, cela importe très rarement. Si la population d’intérêt est importante (p. ex. a plus de 10 entités !), la différence entre l’échantillonnage avec ou sans remise est trop faible pour être prise en compte. La différence entre les échantillons aléatoires simples et les échantillons biaisés, par contre, n’est pas une chose si facile à rejeter.
8.1.3 La plupart des échantillons ne sont pas de simples échantillons aléatoires
Comme vous pouvez le constater en regardant la liste des populations possibles que j’ai présentée ci-dessus, il est presque impossible d’obtenir un échantillon aléatoire simple de la plupart des populations d’intérêt. Quand je fais des expériences, je considérerais comme un petit miracle que mes participants soient un échantillon aléatoire d’étudiants en psychologie de premier cycle de l’université d’Adélaïde, même si c’est de loin la population la plus étroite à laquelle je voudrais généraliser. Une discussion approfondie d’autres types de plans d’échantillonnage dépasse la portée de ce livre, mais pour vous donner une idée de ce qui existe, je vais en énumérer quelques-uns des plus importants.
- Échantillonnage stratifié. Supposons que votre population soit (ou puisse être) divisée en plusieurs sous-populations ou strates différentes. Peut-être menez-vous une étude à plusieurs endroits différents, par exemple. Au lieu d’essayer d’échantillonner au hasard l’ensemble de la population, vous essayez plutôt de prélever un échantillon aléatoire distinct dans chacune des strates. L’échantillonnage stratifié est parfois plus facile à réaliser qu’un simple échantillonnage aléatoire, surtout lorsque la population est déjà divisée en strates distinctes. Il peut aussi être plus efficace qu’un simple échantillonnage aléatoire, surtout lorsque certaines sous-populations sont rares. Par exemple, lorsqu’on étudie la schizophrénie, il vaudrait beaucoup mieux diviser la population en deux45 strates (schizophrène et non schizophrène), puis échantillonner un nombre égal de personnes de chaque groupe. Si vous choisissiez des personnes au hasard, vous obtiendriez si peu de schizophrènes dans l’échantillon que votre étude serait inutile. Ce type particulier d’échantillonnage stratifié est appelé sur échantillonnage parce qu’il constitue une tentative délibérée de surreprésenter des groupes rares.
- L’échantillonnage en boule de neige est une technique particulièrement utile lorsqu’il s’agit d’échantillonner une population « cachée » ou difficile d’accès et est particulièrement courante en sciences sociales. Supposons, par exemple, que les chercheurs souhaitent mener un sondage d’opinion auprès des personnes transgenres. L’équipe de recherche pourrait n’avoir que les coordonnées de quelques personnes transgenres, de sorte que l’enquête commence par leur demander de participer (étape 1). A la fin de l’enquête, les participants sont invités à fournir les coordonnées d’autres personnes qui pourraient souhaiter participer. Au cours de l’étape 2, ces nouveaux contacts font l’objet d’une enquête. Le processus se poursuit jusqu’à ce que les chercheurs aient suffisamment de données.
Le grand avantage de l’échantillonnage en boule de neige est qu’il permet d’obtenir des données dans des situations qu’il serait impossible d’obtenir autrement. Du point de vue statistique, le principal inconvénient est que l’échantillon est particulièrement non aléatoire de sorte qu’il est difficile à traiter. Du côté de la vie réelle, l’inconvénient est que la procédure peut être contraire à l’éthique si elle n’est pas bien gérée, car les populations cachées le sont souvent pour une raison. J’ai choisi les personnes transgenres comme exemple ici pour mettre en évidence cette question. Si vous n’étiez pas prudent, vous pourriez finir par sortir avec des gens qui ne veulent pas être révélés (très mauvaise approche), et même si vous ne faites pas cette erreur, il peut toujours être intrusif d’utiliser les réseaux sociaux des sujets pour les étudier. Il est certainement très difficile d’obtenir le consentement éclairé des gens avant de les contacter, mais dans de nombreux cas, le simple fait de les contacter et de leur dire « Nous voulons vous étudier » peut être blessant. Les réseaux sociaux sont des choses complexes, et ce n’est pas parce que vous pouvez les utiliser pour obtenir des données que vous devriez toujours le faire.
- L’échantillonnage de commodité est plus ou moins ce à quoi il ressemble. Les échantillons sont choisis d’une manière qui convient au chercheur et non au hasard dans la population d’intérêt. L’échantillonnage en boule de neige est un type d’échantillonnage de commodité, mais il en existe beaucoup d’autres. Un exemple courant en psychologie est celui des études qui s’appuient sur des étudiants de premier cycle en psychologie. Ces échantillons sont généralement non aléatoires à deux égards. Premièrement, le fait de se fier aux étudiants de premier cycle en psychologie signifie automatiquement que vos données sont limitées à une seule sous-population. Deuxièmement, les étudiants choisissent habituellement les études auxquelles ils participent, de sorte que l’échantillon est un sous-ensemble auto-sélectionné d’étudiants en psychologie et non un sous-ensemble choisi au hasard. Dans la vie réelle, la plupart des études sont des échantillons de commodité d’une façon ou d’une autre. Il s’agit parfois d’une limite importante, mais pas toujours.
8.1.4 Quelle importance cela a-t-il si vous n’avez pas un échantillon aléatoire simple ?
Bien, la collecte de données du monde réel n’a pas tendance à impliquer des échantillons aléatoires simples et agréables. C’est important ? Un peu de réflexion devrait vous faire comprendre qu’il peut être important que vos données ne soient pas un simple échantillon aléatoire. Pensez simplement à la différence entre les Figure 8‑1 et Figure 8‑2. Cependant, ce n’est pas aussi grave que ça en a l’air. Certains types d’échantillons biaisés ne posent aucun problème. Par exemple, lorsque vous utilisez une technique d’échantillonnage stratifié, vous savez en fait quel est le biais parce que vous l’avez créé délibérément, souvent pour accroître l’efficacité de votre étude, et il existe des techniques statistiques que vous pouvez utiliser pour corriger les biais que vous avez présentés (non couverts dans ce livre !). Donc, dans ces situations, ce n’est pas un problème.
De façon plus générale, cependant, il est important de se rappeler que l’échantillonnage aléatoire est un moyen d’atteindre une fin, et non une fin en soi. Supposons que vous vous êtes fiés à un échantillon de commodité et que, par conséquent, vous pouvez supposer qu’il est biaisé. Un biais dans votre méthode d’échantillonnage ne pose problème que s’il vous amène à tirer des conclusions erronées. De ce point de vue, je dirais que nous n’avons pas besoin que l’échantillon soit généré au hasard à tous les égards, nous avons seulement besoin qu’il soit aléatoire en ce qui concerne le phénomène pertinent sur le plan psychologique qui nous intéresse. Supposons que je fasse une étude sur la capacité de la mémoire de travail. Dans l’étude 1, j’ai en fait la capacité d’échantillonner au hasard tous les êtres humains actuellement vivants, à une exception près : Je ne peux tester que les gens nés le lundi. Dans l’étude 2, je suis en mesure d’échantillonner au hasard la population australienne. Je veux généraliser mes résultats à la population de tous les humains vivants. Quelle étude est la meilleure ? La réponse, évidemment, est l’étude 1. Pourquoi ? Parce que nous n’avons aucune raison de penser qu’être « né un lundi » a un rapport intéressant avec la capacité de mémoire de travail. En revanche, je peux penser à plusieurs raisons pour lesquelles « être Australien » peut avoir de l’importance. L’Australie est un pays riche et industrialisé avec un système éducatif très développé. Les personnes qui ont grandi dans ce système auront vécu des expériences de vie plus semblables à celles des personnes qui ont conçu les tests de capacité de mémoire de travail. Cette expérience commune pourrait facilement se traduire par des croyances similaires sur la façon de passer un test, une supposition commune sur le fonctionnement de l’expérimentation psychologique, et ainsi de suite. Ces choses pourraient avoir de l’importance. Par exemple, le style « passation de test » pourrait avoir appris aux participants australiens à se concentrer exclusivement sur des sujets assez abstraits, beaucoup plus que les personnes qui n’ont pas grandi dans un environnement similaire. Ce pourrait donc induire en erreur sur ce qu’est la capacité de la mémoire de travail. Cela pourrait donc conduire à une image trompeuse de ce qu’est la capacité de mémoire de travail.
Il y a deux points cachés dans cette discussion. Premièrement, lorsque vous concevez vos propres études, il est important de penser à la population à laquelle vous tenez et d’essayer d’échantillonner d’une manière qui convient à cette population. En pratique, vous êtes habituellement obligé de vous contenter d’un « échantillon de convenance » (p. ex. les professeurs de psychologie échantillonnent les étudiants en psychologie parce que c’est la façon la moins coûteuse de recueillir des données, et nos coffres ne débordent pas vraiment d’or), mais si c’est le cas, vous devriez au moins prendre le temps de penser aux dangers que cette pratique pourrait représenter. Deuxièmement, si vous allez critiquer l’étude de quelqu’un d’autre parce qu’il a utilisé un échantillon de convenance plutôt que d’échantillonner laborieusement au hasard toute la population humaine, ayez au moins la courtoisie d’offrir une théorie précise sur la façon dont cela a pu fausser les résultats.
8.1.5 Paramètres de population et statistiques des échantillons
Si l’on met de côté les épineuses questions méthodologiques associées à l’obtention d’un échantillon aléatoire, examinons une question légèrement différente. Jusqu’à présent, nous avons parlé des populations comme le ferait un scientifique. Pour un psychologue, une population peut être un groupe de personnes. Pour un écologiste, une population peut être un groupe d’ours. Dans la plupart des cas, les populations auxquelles s’intéressent les scientifiques sont des choses concrètes qui existent réellement dans le monde réel. Les statisticiens, cependant, sont un drôle de lot. D’une part, ils s’intéressent aux données du monde réel et à la vraie science de la même façon que les scientifiques. D’autre part, ils opèrent également dans le domaine de l’abstraction pure, comme le font les mathématiciens. Par conséquent, la théorie statistique tend à être un peu abstraite concernant la façon dont une population est définie. De la même manière que les chercheurs en psychologie opérationnalisent nos idées théoriques abstraites en termes de mesures concrètes (Section 2.1), les statisticiens opérationnalisent le concept de « population » en termes d’objets mathématiques avec lesquels ils savent comment travailler. Vous avez déjà rencontré ces objets au chapitre 7. C’est ce qu’on appelle des distributions de probabilités.
L’idée est assez simple. Disons qu’on parle de QI. Pour un psychologue, la population d’intérêt est un groupe d’humains qui ont un QI. Un statisticien « simplifie » cela en définissant de façon opérationnelle la population comme étant la distribution de probabilité représentée à la Figure 8‑4a. Les tests de QI sont conçus de manière à ce que le QI moyen soit de 100, que l’écart-type des scores de QI soit de 15 et que la distribution des scores de QI soit normale. Ces valeurs sont appelées paramètres de population parce qu’elles représentent les caractéristiques de l’ensemble de la population. C’est-à-dire que nous disons que la moyenne de la population \(\mu\) est de 100 et que l’écart-type de la population \(\sigma\) est de 15.
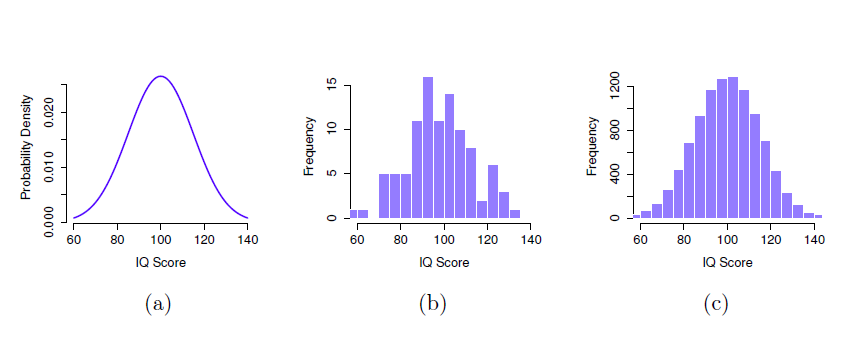
Figure 8‑4 : La distribution de la population des scores de QI (panel a) et deux échantillons tirés au hasard. Dans le panel b, nous avons un échantillon de 100 observations, et dans le panel c, nous avons un échantillon de 10 000 observations.
Supposons que je fasse une expérience. Je sélectionne 100 personnes au hasard et je leur fais passer un test de QI, Figure 8‑4 : Répartition des scores de QI dans la population (panel a) et deux échantillons tirés au hasard. Dans le panel b, nous avons un échantillon de 100 observations, et dans le panel c, nous avons un échantillon de 10 000 observations me donnant un simple échantillon aléatoire de la population. Mon échantillon consisterait en une collection de chiffres comme celle-ci :
106 101 98 80 74 ... 107 72 100
Chacun de ces scores de QI est échantillonné à partir d’une distribution normale avec une moyenne de 100 et un écart-type de 15. Donc, si je trace un histogramme de l’échantillon, j’obtiens quelque chose comme celui illustré à la Figure 8‑4b. Comme vous pouvez le voir, l’histogramme est à peu près de la bonne forme, mais c’est une approximation très grossière de la distribution réelle de la population présentée à la Figure 8‑4a. Lorsque je calcule la moyenne de mon échantillon, j’obtiens un nombre assez proche de la moyenne de la population (100) mais pas identique. Dans ce cas, il s’avère que les personnes de mon échantillon ont un QI moyen de 98,5 et que l’écart-type de leur QI est de 15,9. Ces statistiques d’échantillon sont des propriétés de mon ensemble de données, et bien qu’elles soient assez semblables aux valeurs réelles de la population, elles ne sont pas les mêmes. En général, les statistiques d’échantillon sont les choses que vous pouvez calculer à partir de votre ensemble de données et les paramètres de population sont les choses que vous voulez apprendre. Plus loin dans ce chapitre, je parlerai de la façon dont vous pouvez estimer les paramètres de population à l’aide de vos statistiques d’échantillonnage (section 8.4) et de la façon de déterminer dans quelle mesure vous pouvez faire confiance à vos estimations (section 8.5), mais avant d’y arriver, il y a quelques autres notions à propos de la théorie d’échantillonnage que vous devez connaître.
8.2 La loi des grands nombres
Dans la section précédente, je vous ai montré les résultats d’une expérience fictive de QI avec un échantillon de N « 100. Les résultats étaient quelque peu encourageants puisque la moyenne réelle de la population est de 100 et que la moyenne de l’échantillon de 98,5 est une approximation assez raisonnable de celle-ci. Dans de nombreuses études scientifiques, ce niveau de précision est parfaitement acceptable, mais dans d’autres situations, il faut être beaucoup plus précis. Si nous voulons que nos statistiques d’échantillonnage soient beaucoup plus proches des paramètres de la population, que pouvons-nous faire à ce sujet ?
La réponse évidente est de recueillir plus de données. Supposons que nous ayons mené une expérience beaucoup plus vaste, cette fois en mesurant le QI de 10 000 personnes. Nous pouvons simuler les résultats de cette expérience en utilisant Jamovi. Le fichier IQsim.omv est un fichier de données Jamovi. Dans ce fichier, j’ai généré 10 000 nombres aléatoires échantillonnés à partir d’une distribution normale pour une population avec moyenne = 100 et sd = 15. Ceci a été fait en calculant une nouvelle variable à l’aide de la fonction = NORM(100,15). Un histogramme et un graphique de densité montrent que cet échantillon plus grand est une bien meilleure approximation de la distribution réelle de la population que le plus petit. Cela se reflète dans les statistiques de l’échantillon. Le QI moyen de l’échantillon le plus important est de 99,68 et l’écart-type est de 14,90. Ces valeurs sont maintenant très proches de la population réelle. Voir la Figure 8‑5.
Je me sens un peu bête de dire cela, mais ce que je veux que vous reteniez de tout cela, c’est que les gros échantillons vous donnent généralement de meilleurs renseignements. Je me sens bête de le dire parce que c’est tellement évident que ça ne devrait pas avoir besoin d’être dit. En fait, c’est tellement évident que lorsque Jacob Bernoulli, l’un des fondateurs de la théorie des probabilités, a formalisé cette idée en 1713, il a été un peu bêta sur ce point. Voici comment il a décrit le fait que nous partageons tous cette intuition :
Car même le plus stupide des hommes, par un instinct de nature, seul et sans instruction (ce qui est remarquable), est convaincu que plus on a fait d’observations, moins on risque de s’éloigner de son but (voir Stigler (1986), p65).
D’accord, le passage semble un peu condescendant (pour ne pas dire sexiste), mais son point principal est correct. Il semble vraiment évident que plus de données vous donneront de meilleures réponses. La question est : pourquoi en est-il ainsi ? Il n’est pas surprenant que cette intuition que nous partageons tous s’avère correcte, et les statisticiens l’appellent la loi des grands nombres. La loi des grands nombres est une loi mathématique qui s’applique à de nombreuses statistiques d’échantillons différents, mais la façon la plus simple d’y penser est d’adopter une loi sur les moyennes. La moyenne de l’échantillon est l’exemple le plus évident d’une statistique qui repose sur le calcul de la moyenne (parce que c’est ce qu’est la moyenne… une moyenne), alors voyons cela. Lorsqu’on l’applique à la moyenne de l’échantillon, la loi des grands nombres indique qu’à mesure que l’échantillon s’élargit, la moyenne de l’échantillon tend à se rapprocher de la moyenne réelle de la population. Ou, pour le dire un peu plus précisément, lorsque la taille de l’échantillon «approche» de l’infini (écrit \(N \rightarrow \infty\)), la moyenne de l’échantillon approche la moyenne de la population (\(\overset{\overline{}}{X}\rightarrow \mu)\).46
Je n’ai pas l’intention de vous démontrer que la loi des grands nombres est vraie, mais c’est l’un des outils les plus importants de la théorie statistique. La loi des grands nombres est la chose que nous pouvons utiliser pour justifier notre croyance que la collecte de plus en plus de données nous mènera finalement à la vérité. Pour n’importe quel ensemble de données particulier, les statistiques d’échantillon que nous calculons à partir de celui-ci seront erronées, mais la loi des grands nombres nous dit que si nous continuons à recueillir plus de données, ces statistiques d’échantillon auront tendance à se rapprocher de plus en plus des véritables paramètres démographiques.
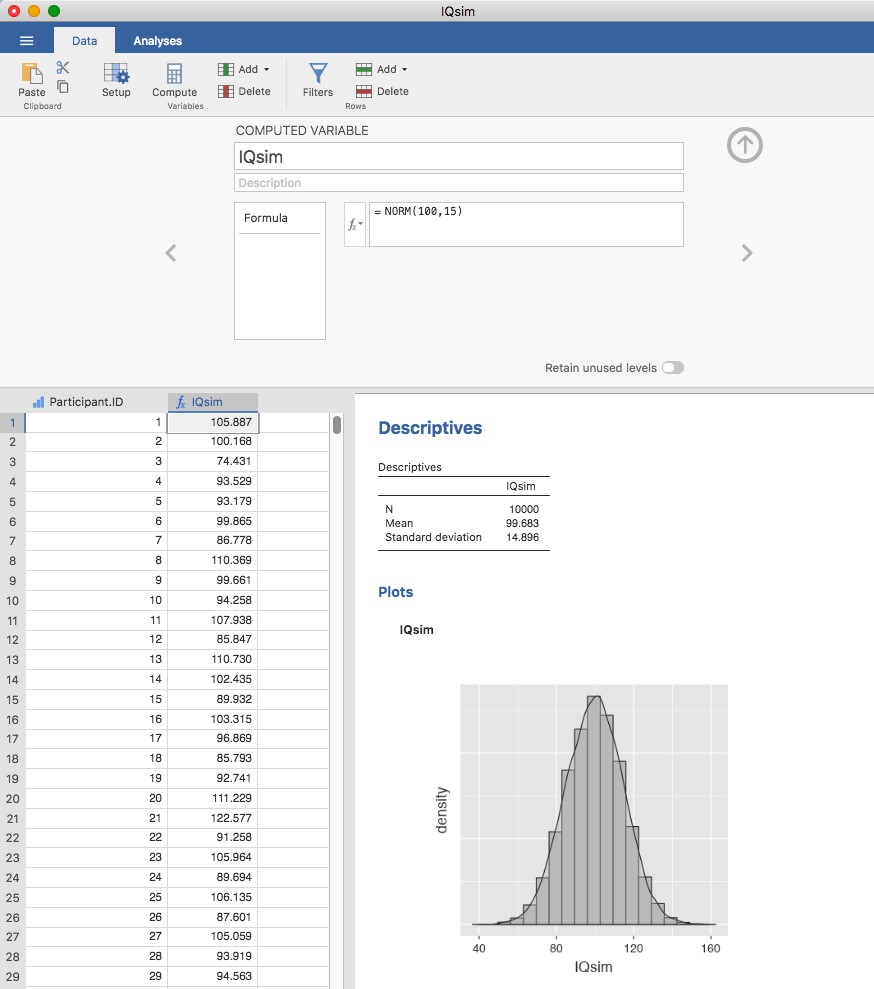
Figure 8‑5 : Un échantillon aléatoire tiré d’une distribution normale à l’aide de Jamovi
8.3 Les distributions d’échantillonnage et le théorème de la limite centrale
La loi des grands nombres est un outil très puissant, mais elle ne suffira pas à répondre à toutes nos questions. Il ne nous donne entre autres qu’une « garantie à long terme ». À long terme, si nous étions en mesure de recueillir une quantité infinie de données, la loi des grands nombres garantirait que nos statistiques d’échantillonnage seraient exactes. Mais comme John Maynard Keynes l’a fait valoir en économie, une garantie à long terme n’est guère utile dans la vie réelle.
[Le] long terme est un guide trompeur de l’actualité. À long terme, nous sommes tous morts. Les économistes se fixent une tâche trop facile, trop inutile, s’ils ne peuvent nous dire, en période de tempête, que lorsque la tempête est passée depuis longtemps, l’océan est à nouveau plat. (Keynes (2009), p. 80)
Comme en économie, il en va de même en psychologie et en statistique. Il ne suffit pas de savoir que nous parviendrons éventuellement à la bonne réponse lors du calcul de la moyenne de l’échantillon. Savoir qu’un ensemble de données infiniment grand me dira la valeur exacte de la moyenne de la population est peu réconfortant lorsque mon ensemble de données réelles a une taille d’échantillon de N = 100. Dans la vraie vie, il faut donc savoir quelque chose sur le comportement de la moyenne de l’échantillon lorsqu’elle est calculée à partir d’un ensemble de données plus modeste !
8.3.1 Distribution d’échantillonnage de la moyenne
Dans cette optique, abandonnons l’idée que nos études auront des échantillons de 10 000 personnes et considérons plutôt qu’il s’agit d’une expérience très modeste. Cette fois-ci, nous allons échantillonner N = 5 personnes et mesurer leur QI. Comme avant, je peux simuler cette expérience avec la fonction Jamovi = NORM(100,15), mais je n’ai besoin que de 5 ID de participants cette fois-ci, pas 10 000. Ce sont les cinq nombres que Jamovi a générés :
90 82 94 99 110
Le QI moyen dans cet échantillon s’avère être exactement 95. Il n’est donc pas surprenant que ce soit beaucoup moins précis que l’expérience précédente. Imaginez maintenant que j’ai décidé de reproduire l’expérience. C’est-à-dire que je répète la procédure le plus fidèlement possible et que j’échantillonne au hasard 5 nouvelles personnes et mesure leur QI. Encore une fois, Jamovi me permet de simuler les résultats de cette procédure, et génère ces cinq nombres :
78 88 111 111 117
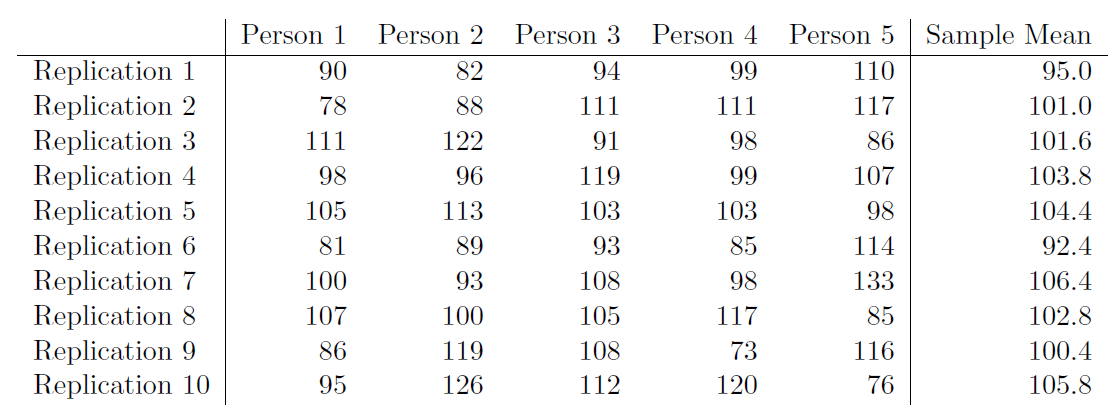
Cette fois, le QI moyen de mon échantillon est de 101. Si je répète l’expérience 10 fois, j’obtiens les résultats indiqués dans le Tableau 8‑1, et comme vous pouvez le constater, la moyenne de l’échantillon varie d’une réplication à l’autre.
Supposons maintenant que j’ai décidé de continuer dans cette voie, en reproduisant encore et encore cette expérience des « cinq scores de QI ». Chaque fois que je répète l’expérience, je note l’exemple du Tableau 8‑1 : Dix répétitions de l’expérience de QI, chacune avec une taille d’échantillon de N = 5. Je rapporte la moyenne de l’échantillon
Tableau 8‑1 : 10 répétition de l’expérience sur les QI avec un échantillon de taille N=5
Avec le temps, j’accumulerais un nouvel ensemble de données, dans lequel chaque expérience génère un seul point de données. Les 10 premières observations de mon ensemble de données sont les moyennes de l’échantillon énumérées au Tableau 8‑1, de sorte que mon ensemble de données commence comme ceci :
95.0 101.0 101.6 103.8 104.4 ...
Et si je continuais comme ça pendant 10 000 répétitions, et que je faisais un histogramme. C’est exactement ce que j’ai fait, et vous pouvez voir les résultats à la Figure 8‑6. Comme l’illustre cette figure, la moyenne de 5 QI se situe habituellement entre 90 et 110. Mais plus important encore, ce qu’il met en évidence, c’est que si nous répétons une expérience encore et encore, nous nous retrouvons avec une distribution de moyennes d’échantillons ! Cette distribution a un nom spécial dans les statistiques, elle s’appelle la distribution d’échantillonnage de la moyenne.
Les distributions d’échantillonnage sont une autre idée théorique importante en statistique, et elles sont cruciales pour comprendre le comportement des petits échantillons. Par exemple, lorsque j’ai fait la toute première expérience des « cinq scores de QI », la moyenne de l’échantillon s’est avérée être de 95. Ce que la distribution d’échantillonnage de la Figure 8‑6 nous indique, cependant, c’est que l’expérience des « cinq scores de QI » n’est pas très précise. Si je répète l’expérience, la distribution d’échantillonnage me dit que je peux m’attendre à voir une moyenne d’échantillon entre 80 et 120.
8.3.2 Il existe des distributions d’échantillonnage pour n’importe quelle statistique d’échantillonnage !
Une chose à garder à l’esprit lorsque vous songez aux distributions d’échantillonnage est que toute statistique d’échantillonnage que vous pourriez vouloir calculer à une distribution d’échantillonnage. Par exemple, supposons que chaque fois que je répète l’expérience des « cinq scores de QI », je note le plus grand score de QI de l’expérience. Cela me donnerait un ensemble de données qui a commencé comme ça :
110 117 122 119 113...
Faire cela encore et encore me donnerait une distribution d’échantillonnage très différente, à savoir la distribution d’échantillonnage du maximum.
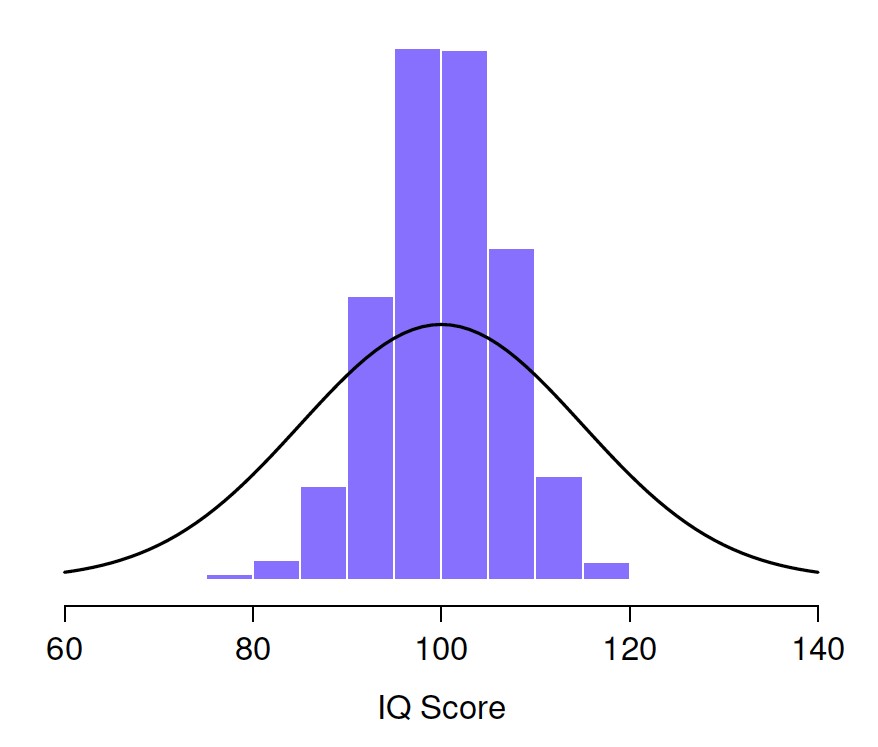
Figure 8‑6 : Distribution d’échantillonnage de la moyenne de « l’expérience des cinq scores de QI ». Si vous échantillonnez 5 personnes au hasard et calculez leur QI moyen, vous obtiendrez presque certainement un nombre entre 80 et 120, même s’il y a beaucoup d’individus qui ont un QI supérieur à 120 ou inférieur à 80. À titre de comparaison, la ligne noire représente la distribution des scores de QI dans la population.
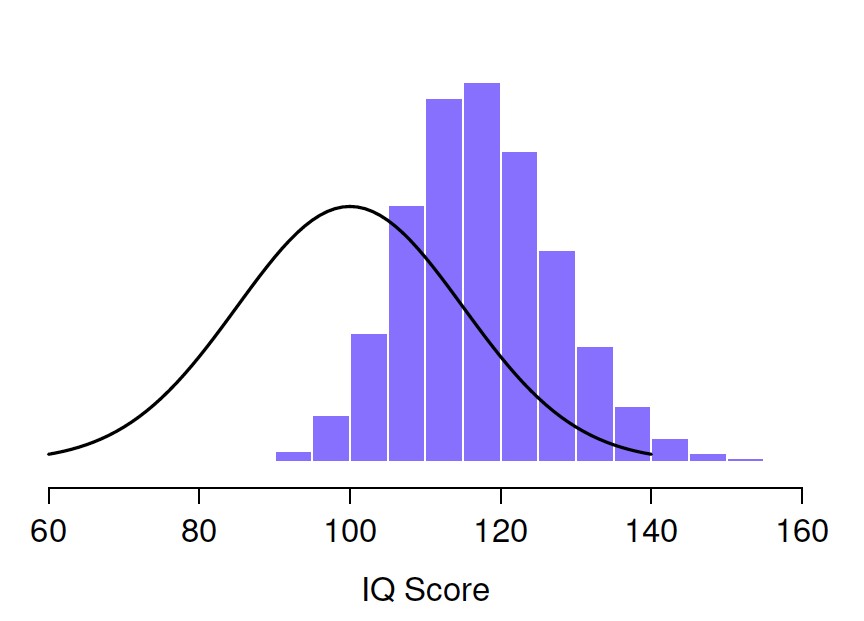
Figure 8‑7 : La distribution d’échantillonnage du maximum pour l’«expérience des cinq scores de QI». Si vous échantillonnez 5 personnes au hasard et choisissez celle qui a le QI le plus élevé, vous verrez probablement quelqu’un avec un QI entre 100 et 140.
La distribution d’échantillonnage du maximum de 5 QI est illustrée à la Figure 8‑7. Il n’est pas surprenant que si vous choisissez 5 personnes au hasard et que vous trouvez ensuite la personne ayant le QI le plus élevé, elles auront un QI supérieur à la moyenne. La plupart du temps, vous vous retrouverez avec quelqu’un dont le QI se situe entre 100 et 140.
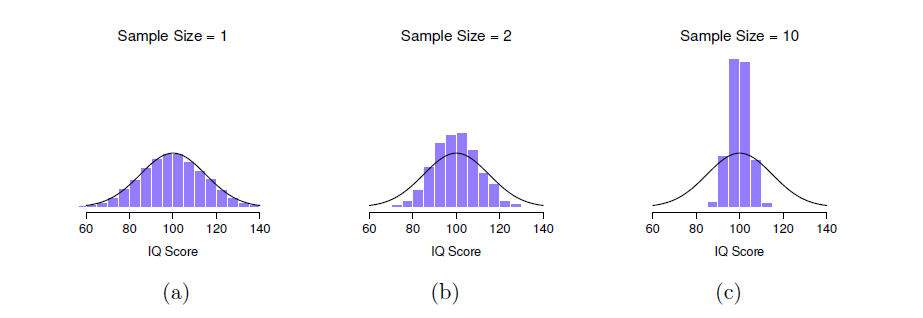
Figure 8‑8 : Une illustration de la façon dont la distribution d’échantillonnage de la moyenne dépend de la taille de l’échantillon. Dans chaque panel, j’ai généré 10 000 échantillons de données sur le QI et calculé le QI moyen observé dans chacun de ces ensembles de données. Les histogrammes de ces placettes montrent la distribution de ces moyennes (c.-à-d. la distribution d’échantillonnage de la moyenne). Chaque score de QI individuel a été tiré d’une distribution normale avec une moyenne de 100 et un écart-type de 15, qui est représenté par la ligne noire pleine. Dans le panel a, chaque ensemble de données ne contenait qu’une seule observation, de sorte que la moyenne de chaque échantillon n’est que le QI d’une personne. Par conséquent, la distribution d’échantillonnage de la moyenne est bien sûr identique à la distribution de la population des scores de QI. Cependant, lorsque nous augmentons la taille de l’échantillon à 2, la moyenne d’un échantillon tend à être plus proche de la moyenne de la population que du quotient intellectuel d’une personne, de sorte que l’histogramme (c.-à-d. la distribution d’échantillonnage) est un peu plus étroit que la distribution dans la population. Lorsque nous portons la taille de l’échantillon à 10 (panel c), nous constatons que la distribution des moyennes de l’échantillon tend à être assez étroitement concentrée autour de la moyenne réelle de la population.
8.3.3 Le théorème de la limite centrale
Pour l’instant, j’espère que vous avez une bonne idée de ce que sont les distributions d’échantillonnage, et en particulier de la distribution d’échantillonnage de la moyenne. Dans cette section, je veux parler de la façon dont la distribution d’échantillonnage de la moyenne change en fonction de la taille de l’échantillon. Intuitivement, vous connaissez déjà une partie de la réponse. Si vous n’avez que quelques observations, la moyenne de l’échantillon est susceptible d’être assez imprécise. Si vous répliquez une petite expérience et recalculez la moyenne, vous obtiendrez une réponse très différente. En d’autres termes, la distribution d’échantillonnage est assez large. Si vous répliquez une grande expérience et recalculez la moyenne de l’échantillon, vous obtiendrez probablement la même réponse que la dernière fois, donc la distribution d’échantillonnage sera très étroite. Vous pouvez le voir visuellement à la Figure 8‑8, qui montre que plus la taille de l’échantillon est grande, plus la distribution d’échantillonnage est étroite. Nous pouvons quantifier cet effet en calculant l’écart-type de la distribution d’échantillonnage, qu’on appelle l’erreur type. L’erreur-type d’une statistique est souvent appelée SE, et comme nous nous intéressons habituellement à l’erreur-type de la moyenne de l’échantillon, nous utilisons souvent l’acronyme SEM. Comme vous pouvez le voir, rien qu’en regardant l’image, plus la taille de l’échantillon N augmente, plus le SEM diminue.
Bien, c’est une partie de l’histoire. Cependant, il y a quelque chose que j’ai négligé jusqu’ici. Tous mes exemples jusqu’ici ont été basés sur les expériences de « IQ scores », et parce que les scores de QI sont à peu près normalement distribués, j’ai supposé que la distribution de la population est normale. Et si ce n’est pas normal ? Qu’arrive-t-il à la distribution d’échantillonnage de la moyenne ? Ce qui est remarquable, c’est que, quelle que soit la forme de votre distribution de population, Lorsque N augmente la distribution d’échantillonnage de la moyenne commence à ressembler davantage à une distribution normale. Pour vous donner une idée, j’ai fait quelques simulations. Pour ce faire, j’ai commencé avec la distribution « cumulée" montrée dans l’histogramme de la Figure 8‑9. Comme vous pouvez le voir en comparant l’histogramme de forme triangulaire à la courbe en cloche tracée par la ligne noire, la distribution de la population ne ressemble pas du tout à une distribution normale. Ensuite, j’ai simulé les résultats d’un grand nombre d’expériences. Dans chaque expérience, j’ai prélevé N = 2 échantillons de cette distribution, puis j’ai calculé la moyenne de l’échantillon. La Figure 8‑9b présente l’histogramme de ces moyennes d’échantillonnage (c.-à-d. la distribution d’échantillonnage de la moyenne pour N = 2). Cette fois, l’histogramme produit une distribution en cloche. Ce n’est toujours pas normal, mais c’est beaucoup plus près de la ligne noire que la distribution de la population à la Figure 8‑9a. Lorsque j’augmente la taille de l’échantillon à N = 4, la distribution d’échantillonnage de la moyenne est très proche de la normale (Figure 8‑9c), et au moment où nous atteignons une taille d’échantillon de N = 8, elle est presque parfaitement normale. En d’autres termes, tant que la taille de votre échantillon n’est pas minuscule, la distribution d’échantillonnage de la moyenne sera à peu près normale, peu importe à quoi ressemble la distribution de votre population !
Sur la base de ces chiffres, il semble que nous ayons des preuves pour toutes les allégations suivantes concernant la distribution d’échantillonnage de la moyenne.
- La moyenne de la distribution d’échantillonnage est la même que la moyenne de la population.
- L’écart-type de la distribution d’échantillonnage (c.-à-d. l’erreur type) diminue à mesure que la taille de l’échantillon augmente.
- La forme de la distribution d’échantillonnage devient normale à mesure que la taille de l’échantillon augmente.
En fait, non seulement ces affirmations sont vraies, mais il existe un théorème très célèbre en statistique qui prouve les trois, il est connu sous le nom de théorème de la limite centrale. Entre autres choses, le théorème de la limite centrale nous dit que si la distribution de la population a une moyenne µ et un écart-type \(\sigma\), alors la distribution d’échantillonnage de la moyenne a aussi une moyenne \(\mu\) et l’erreur type de la moyenne est
\[ SEM = \frac{\sigma}{\sqrt{N}} \]
Comme nous divisons l’écart-type de la population \(\sigma\) par la racine carrée de la taille de l’échantillon N, le SEM diminue à mesure que la taille de l’échantillon augmente. Il nous indique également que la forme de la distribution d’échantillonnage devient normale.47
Ce résultat est utile pour toutes sortes de choses. Il nous dit pourquoi les grandes expériences sont plus fiables que les petites, et parce qu’il nous donne une formule explicite pour l’erreur type, il nous dit à quel point une grande expérience est beaucoup plus fiable. Il nous dit pourquoi la distribution normale est, bien sûr, normale.
Dans les expériences réelles, bon nombre des choses que nous voulons mesurer sont en fait des moyennes de d’ensemble de quantités différentes (p. ex. l’intelligence « générale », telle que mesurée par le QI, est une moyenne d’un grand nombre de compétences et d’aptitudes « spécifiques »), et lorsque cela se produit, la quantité moyenne devrait suivre une distribution normale. En raison de cette loi mathématique, la distribution normale apparaît encore et encore dans les données réelles.
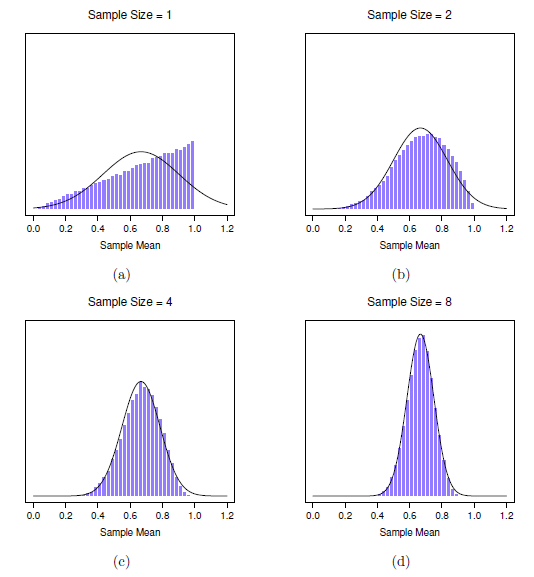
Figure 8‑9 : Démonstration du théorème de la limite centrale. Dans le panel a, nous avons une distribution non normale de la population, et les panels b-d montrent la distribution d’échantillonnage de la moyenne pour les échantillons de taille 2,4 et 8 pour les données tirées de la distribution du panel a. Comme vous pouvez le voir, même si la distribution originale de la population est non normale, la distribution d’échantillonnage de la moyenne devient assez proche de la normale lorsque vous avez un échantillon même de quatre observations.
8.4 Estimation des paramètres de population
Dans tous les exemples de QI présentés dans les sections précédentes, nous connaissions à l’avance les paramètres de la population. Comme tous les étudiants de premier cycle reçoivent leur tout premier cours sur la mesure de l’intelligence, les scores de QI sont définis comme ayant une moyenne de 100 et un écart-type de 15. Cependant, c’est un peu un mensonge. Comment savoir si les scores de QI ont une moyenne réelle de 100 dans la population ? Eh bien, nous le savons parce que les personnes qui ont conçu les tests les ont administrés à de très gros échantillons et qu’elles ont ensuite « truqué » les règles de notation pour que leur échantillon ait une moyenne de 100. Ce n’est pas une mauvaise chose bien sûr, c’est une partie importante de la conception d’une mesure psychologique. Cependant, il est important de garder à l’esprit que cette moyenne théorique de 100 ne s’applique qu’à la population que les concepteurs des tests ont utilisée pour concevoir les tests. Les bons concepteurs de tests s’efforceront en fait de fournir des « normes de test » qui peuvent s’appliquer à un grand nombre de populations différentes (par exemple, différents groupes d’âge, nationalités, etc.).
C’est très pratique, mais bien sûr, presque tous les projets de recherche d’intérêt impliquent l’examen d’une population de personnes différentes de celles qui sont utilisées dans les normes d’essai. Supposons, par exemple, que vous vouliez mesurer l’effet de l’intoxication saturnine à faible concentration sur le fonctionnement cognitif à Port Pirie, une ville industrielle d’Australie-Méridionale où se trouve une fonderie de plomb. Peut-être décidez-vous de comparer les scores de QI des habitants de Port Pirie à ceux d’un échantillon comparable de Whyalla, une ville industrielle d’Australie-Méridionale dotée d’une raffinerie d’acier.48 Peu importe la ville à laquelle vous pensez, il n’est pas logique de supposer simplement que la vraie population a un QI moyen de 100. Personne n’a, à ma connaissance, produit de données de normalisation sensées qui peuvent être automatiquement appliquées aux villes industrielles d’Australie-Méridionale. Nous allons devoir estimer les paramètres de la population à partir d’un échantillon de données. Alors, comment fait-on ça ?
8.4.1 Estimation de la moyenne de la population
Supposons que nous allions à Port Pirie et que 100 habitants de la région aient la gentillesse de passer un test de QI. Le QI moyen de ces personnes s’avère être \(\bar{X}\)=98,5. Quel est donc le vrai QI moyen pour l’ensemble de la population de Port Pirie ? De toute évidence, nous ne connaissons pas la réponse à cette question. Cela pourrait être 97,2, mais cela pourrait aussi être 103,5. Notre échantillonnage n’est pas exhaustif et nous ne pouvons donc pas donner une réponse définitive. Néanmoins, si j’étais forcé, sous la menace d’une arme à feu, de donner une « meilleure estimation », je dirais 98,5. C’est l’essence même de l’estimation statistique : donner la meilleure estimation possible.
Dans cet exemple, l’estimation du paramètre inconnu d’une population est simple. Je calcule la moyenne de l’échantillon et je m’en sers comme estimation de la moyenne de la population. C’est assez simple, et dans la prochaine section, je vais expliquer la justification statistique de cette réponse intuitive. Toutefois, pour l’instant, ce que je veux faire, c’est m’assurer que vous reconnaissez que la statistique de l’échantillon et l’estimation du paramètre population sont des choses conceptuellement différentes. Un échantillon statistique est une description de vos données, alors que l’estimation n’est qu’une estimation de la population. Dans cet esprit, les statisticiens utilisent souvent des notations différentes pour s’y référer. Par exemple, si la moyenne réelle de la population est notée µ, alors nous utiliserons \(\hat{\mu}\) pour nous référer à notre estimation de la moyenne de la population. Par contre, la moyenne de l’échantillon est notée \(\bar{X}\) ou parfois m. Cependant, dans les échantillons aléatoires simples, l’estimation de la moyenne de la population est identique à la moyenne de l’échantillon. Si j’observe une moyenne d’échantillon de \(\bar{X}\) = 98,5 alors mon estimation de la moyenne de population est aussi \(\hat{\mu}=98.5\). Pour aider à garder la notation claire, voici un tableau pratique :
| Symbole | Qu’est-ce que c’est ? | On sait ce que c’est ? |
| \(\bar{X}\) | Moyenne de l’éch | antillon | Oui, calculée à | partir des données brutes |
| \(\mu\) | Moyenne réelle de la population |
Presque jamais connue avec certitude |
| \(\hat{\mu}\) | Estimation de la moyenne de la population | Oui, identique à la moyenne de l’échantillon dans les échantillons aléatoires simples |
8.4.2 Estimation de l’écart-type de la population
Jusqu’à présent, l’estimation semble assez simple, et vous vous demandez peut-être pourquoi je vous ai forcé à lire tous ces trucs sur la théorie de l’échantillonnage. Dans le cas de la moyenne, notre estimation du paramètre de population (c.-à-d. \(\hat{\mu}\)) s’est avérée identique à celle de l’échantillon statistique correspondant (c.-à-d. \(\bar{X}\)). Cependant, ce n’est pas toujours vrai. Pour voir cela, réfléchissons à la façon de construire une estimation de l’écart-type de la population, que nous indiquerons à \(\hat{\sigma}\). Que devons-nous utiliser comme estimation dans ce cas ? Votre première pensée pourrait être que nous pourrions faire la même chose que pour l’estimation de la moyenne, et utiliser simplement la statistique de l’échantillon comme estimation. C’est presque la bonne chose à faire, mais pas tout à fait.
Voilà pourquoi. Supposons que j’ai un échantillon qui contient une seule observation. Pour cet exemple, il est utile de considérer un échantillon où vous n’avez aucune intuition sur ce que pourraient être les vraies valeurs de la population, alors utilisons quelque chose de complètement fictif. Supposons que l’observation en question mesure la cromulence de mes chaussures. Il s’avère que mes chaussures ont une cromulence de 20. Voilà mon échantillon :
20
C’est un échantillon parfaitement légitime, même s’il a une taille d’échantillon de N = 1. Il a une moyenne d’échantillon de 20 et parce que chaque observation dans cet échantillon est égale à la moyenne de l’échantillon (évidemment !) il a un écart type d’échantillon de 0. Comme une description de l’échantillon cela semble tout à fait juste, l’échantillon contient une seule observation et donc aucune variation observée dans l’échantillon. Un écart-type d’échantillon de s = 0 est ici la bonne réponse. Mais en tant qu’estimation de l’écart-type de la population, cela parait complètement fou, ne croyez-vous pas ? Certes, vous et moi ne savons rien du tout de ce qu’est la « cromulence », mais nous savons quelque chose des données. La seule raison pour laquelle nous ne voyons aucune variabilité dans l’échantillon est que l’échantillon est trop petit pour afficher une variation ! Donc, si vous avez un échantillon de taille N = 1, vous avez l’impression que la bonne réponse est simplement de dire « aucune idée du tout ».
Remarquez que vous n’avez pas la même intuition lorsqu’il s’agit de la moyenne de l’échantillon et de la moyenne de la population. S’il est forcé de faire une meilleure estimation de la population, cela signifie qu’il n’est pas complètement insensé de deviner que la moyenne de la population est de 20. Bien sûr, vous ne vous sentiriez probablement pas très confiant dans cette supposition parce que vous n’avez qu’une seule observation sur laquelle travailler, mais c’est quand même la meilleure supposition que vous pouvez faire.
Étendons un peu cet exemple. Supposons maintenant que je fasse une deuxième observation. Mon ensemble de données contient maintenant N = 2 observations de la cromulence des chaussures, et l’échantillon complet ressemble maintenant à ceci :
20, 22
Cette fois-ci, notre échantillon est juste assez grand pour nous permettre d’observer une certaine variabilité : deux observations est le nombre minimum nécessaire pour qu’une variabilité puisse être observée ! Pour notre nouvel ensemble de données, la moyenne de l’échantillon est \[\overset{\overline{}}{X}\] = 21, et l’écart-type de l’échantillon est s = 1. Encore une fois, pour ce qui est de la moyenne de la population, la meilleure estimation que nous puissions faire est la moyenne de l’échantillon. Si nous devions deviner, nous devinerions probablement que la cromulence moyenne de la population est de 21. Qu’en est-il de l’écart-type ? C’est un peu plus compliqué. L’écart-type de l’échantillon n’est basé que sur deux observations, et si vous êtes comme moi, vous avez probablement l’intuition que, avec seulement deux observations, nous n’avons pas donné à la population « assez de chance » pour nous révéler sa véritable variabilité. Ce n’est pas seulement que nous soupçonnons que l’estimation est erronée, après tout, avec seulement deux observations, nous nous attendons à ce qu’elle le soit dans une certaine mesure. L’inquiétude est que l’erreur est systématique. Plus précisément, nous soupçonnons que l’écart-type de l’échantillon est probablement inférieur à celui de la population.
Cette intuition semble juste, mais ce serait bien de le démontrer d’une manière ou d’une autre. Il existe en fait des preuves mathématiques qui confirment cette intuition, mais à moins d’avoir le bon bagage mathématique, elles n’aident pas beaucoup. Je vais plutôt simuler les résultats de quelques expériences. Dans cet esprit, revenons à nos études sur le QI. Supposons que le QI moyen de la population réelle est de 100 et que l’écart-type est de 15. Je vais d’abord faire une expérience dans laquelle je mesure N = 2 scores de QI et je vais calculer l’écart-type de l’échantillon. Si je le fais encore et encore, et que je trace un histogramme de ces écarts-types d’échantillon, ce que j’ai, c’est la distribution d’échantillonnage de l’écart type. J’ai tracé cette distribution dans la Figure 8‑10. Même si l’écart type réel de la population est de 15, la moyenne des écarts types de l’échantillon n’est que de 8,5. Remarquez qu’il s’agit d’un résultat très différent de celui que nous avons obtenu à la Figure 8‑8b lorsque nous avons tracé la distribution d’échantillonnage de la moyenne, où la moyenne de la population est de 100 et la moyenne des moyennes de l’échantillon est également de 100.
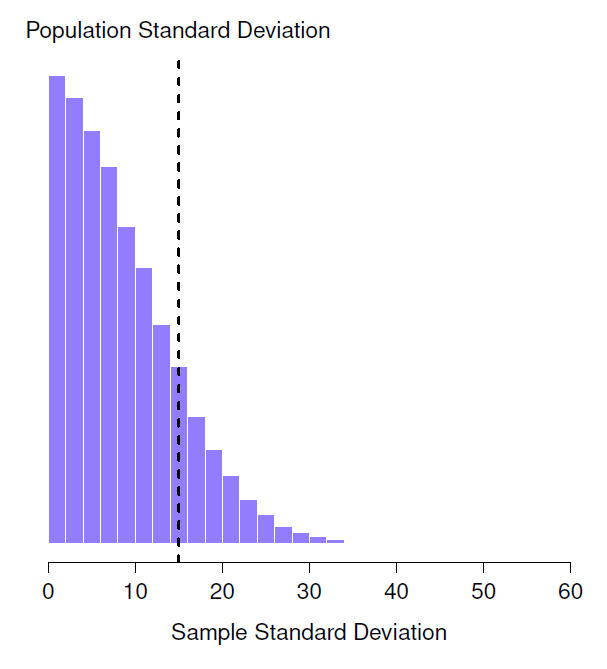
Figure 8‑10 : Distribution d’échantillonnage de l’écart-type de l’échantillon pour une expérience à «deux scores de QI». L’écart-type réel de la population est de 15 (ligne pointillée), mais comme vous pouvez le voir sur l’histogramme, la grande majorité des expériences produiront un écart-type de l’échantillon beaucoup plus petit que celui-ci. En moyenne, cette expérience produirait un écart-type d’échantillon de seulement 8,5, bien en dessous de la valeur réelle ! En d’autres termes, l’écart-type de l’échantillon est une estimation biaisée de l’écart-type de la population.
Maintenant, étendons la simulation. Au lieu de nous limiter à la situation où N = 2, répétons l’exercice pour les tailles d’échantillon de 1 à 10. Si nous traçons la moyenne et l’écart-type moyen de l’échantillon en fonction de la taille de l’échantillon, nous obtenons les résultats présentés à la Figure 8‑11. Sur le côté gauche (panneau a) j’ai tracé la moyenne des moyennes des échantillons et sur le côté droit (panneau b) j’ai tracé l’écart type moyen. Les deux graphiques sont très différents : en moyenne, la moyenne de l’échantillon moyen est égale à la moyenne de la population. Il s’agit d’un estimateur non biaisé, ce qui explique essentiellement pourquoi votre meilleure estimation de la moyenne de la population est la moyenne de l’échantillon49. Le graphique de droite est très différent : en moyenne, l’écart-type s de l’échantillon est inférieur à l’écart-type de la population \(\sigma\). C’est un estimateur biaisé. En d’autres termes, si nous voulons faire une « meilleure estimation » \(\hat{\sigma}\) de la valeur de l’écart-type de la population \(\sigma\) nous devons nous assurer que notre estimation est un peu plus grande que l’écart-type s de l’échantillon.
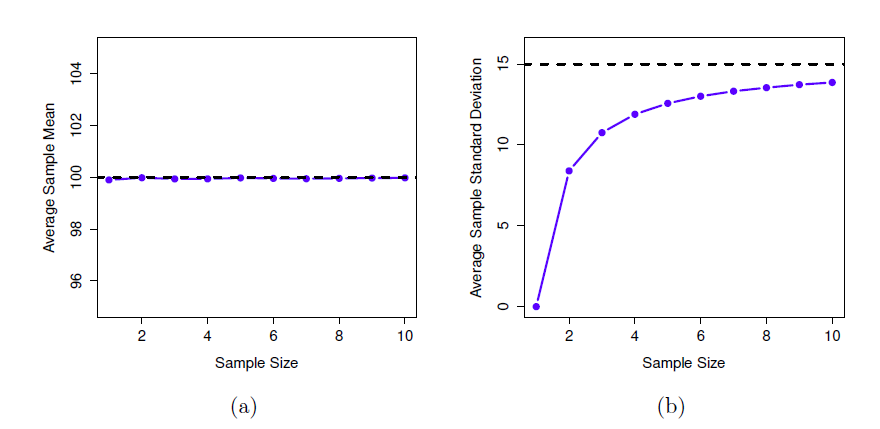
Figure 8‑11 : Illustration du fait que la moyenne de l’échantillon est un estimateur non biaisé de la moyenne de la population (panel a), mais que l’écart-type de l’échantillon est biaisé (panel b). Pour la figure, j’ai généré 10 000 ensembles de données simulées avec 1 observation chacun, 10 000 autres avec 2 observations, et ainsi de suite jusqu’à une taille d’échantillon de 10. Chaque ensemble de données était constitué de fausses données sur le QI, c’est-à-dire que les données étaient normalement distribuées avec une moyenne de population réelle de 100 et un écart type de 15. En moyenne, la moyenne de l’échantillon est de 100, quelle que soit la taille de l’échantillon (panel a). Cependant, les écarts-types des échantillons s’avèrent systématiquement trop faibles (panel b), en particulier pour les petites tailles d’échantillons.
La solution à ce biais systématique s’avère très simple. Voici comment ça marche. Avant d’aborder l’écart-type, examinons la variance. Si vous vous souvenez de la section 4.2, la variance de l’échantillon est définie comme étant la moyenne des écarts quadratiques de la moyenne de l’échantillon. C’est à dire :
\[ s^{2} = \frac{1}{N}\sum_{i = 1}^{N}\left( X_{i} -\bar{X} \right)^{2} \]
La variance d’échantillon \(s^{2}\) est un estimateur biaisé de la variance de la population \(\sigma^{2}\) Mais il s’avère que nous n’avons qu’à faire un tout petit ajustement pour transformer cela en un estimateur non biaisé. Tout ce que nous avons à faire est de diviser par N-1 plutôt que par N. Si nous faisons cela, nous obtenons la formule suivante :
\[ {\hat{\sigma}}^{2} = \frac{1}{N - 1}\sum_{i = 1}^{N}\left( X_{i} - \bar{X} \right)^{2} \]
Il s’agit d’un estimateur non biaisé de la variance de la population \(\sigma\). En outre, cela répond enfin à la question que nous avons soulevée à la section 4.2. Pourquoi Jamovi nous a-t-il donné des réponses légèrement différentes pour la variance ? C’est parce que Jamovi calcule \[{\hat{\sigma}}^{2}\] pas s2, voilà pourquoi. Il en va de même pour l’écart-type. Si nous divisons par N - 1 au lieu de N, notre estimation de l’écart-type de la population devient :
\[ \hat{\sigma} = \sqrt{\frac{1}{N - 1}\sum_{i = 1}^{N}\left( X_{i} - \bar{X} \right)^{2}} \]
et lorsque nous utilisons la fonction d’écart-type intégrée de Jamovi, ce qu’il fait est de calculer \(\hat{\sigma}\), pas s. a50
Un dernier point. Dans la pratique, beaucoup de gens ont tendance à se référer à \(\hat{\sigma}\). (c.-à-d. la formule où nous divisons par N-1) comme écart-type de l’échantillon. Techniquement, c’est incorrect. L’écart-type de l’échantillon devrait être égal à s (c.-à-d. la formule où nous divisons par N). Ce n’est pas la même chose, que ce soit sur le plan conceptuel ou numérique. L’une est une propriété de l’échantillon, l’autre est une caractéristique estimée de la population. Cependant, dans presque toutes les applications de la vie réelle, ce qui nous préoccupe réellement, c’est l’estimation du paramètre de population, et donc les gens rapportent toujours \(\hat{\sigma}\) plutôt que s. C’est le bon chiffre à rapporter, bien sûr. C’est juste que les gens ont tendance à être un peu imprécis au sujet de la terminologie lorsqu’ils la rédigent, parce que « l’écart-type de l’échantillon » est plus court que « l’écart-type estimé de la population ». Ce n’est pas grand-chose, et en pratique, je fais la même chose que tout le monde. Néanmoins, je pense qu’il est important de garder les deux concepts séparés. Ce n’est jamais une bonne idée de confondre les « propriétés connues de votre échantillon » avec les « suppositions sur la population dont il provient ». Dès que vous commencez à penser que s et \(\hat{\sigma}\) sont la même chose, vous commencez à faire exactement cela.
Pour terminer cette section, voici quelques autres tableaux qui vous aideront à clarifier les choses.
| Symbole | Qu’est-ce que c’est ? | On sait ce que c’est ? |
| \(s\) | Écart-type de l’échantillon | Oui, calculé à partir des données brutes |
| \(\sigma\) | Écart-type de la population | Presque jamais connu avec certitude |
| \(\hat{\sigma}\) | Estimation de l’écart-type de la population | Oui, mais ce n’est pas la même chose que l’écart-type de l’échantillon |
| Symbole | Qu’est-ce que c’est ? | On sait ce que c’est ? |
| \(s^{2}\) | Variance de l’échantillon | Oui, calculé à partir des données brutes |
| \(\sigma^{2}\) | Variation de la population | Presque jamais connu avec certitude |
| \(\hat{\sigma}^{2}\) | Estimation de la variation de la population | Oui, mais ce n’est pas la même chose que la variance de l’échantillon |
8.5 Estimation d’un intervalle de confiance
Les statistiques, c’est de ne jamais avoir à dire qu’on est certain - Origine inconnue51
Jusqu’à présent, dans ce chapitre, j’ai exposé les principes de base de la théorie de l’échantillonnage sur lesquels se fondent les statisticiens pour deviner les paramètres de la population à partir d’un échantillon de données. Comme l’illustre cette discussion, l’une des raisons pour lesquelles nous avons besoin de toute cette théorie de l’échantillonnage est que chaque ensemble de données nous laisse avec une certaine incertitude, de sorte que nos estimations ne seront jamais parfaitement exactes. Ce qui manque dans cette discussion, c’est une tentative de quantifier le degré d’incertitude qui s’attache à notre estimation. Il ne suffit pas de deviner que, disons, le QI moyen des étudiants en psychologie de premier cycle est de 115 (oui, je viens d’inventer ce chiffre). Nous voulons aussi pouvoir dire quelque chose qui exprime le degré de certitude que nous avons à son propos. Par exemple, il serait bien de pouvoir dire qu’il y a 95% de chances que la vraie moyenne se situe entre 109 et 121. Le nom pour ceci est un intervalle de confiance pour la moyenne.
Armé d’une compréhension des distributions d’échantillonnage, l’établissement d’un intervalle de confiance pour la moyenne est en fait assez facile. Voici comment ça marche. Supposons que la vraie moyenne de la population est \(\mu\) et que l’écart-type est \(\sigma\). Je viens de terminer mon étude qui a N participants, et le QI moyen parmi ces participants est \(\bar{X}\). Notre analyse du théorème de la limite centrale (section 8.3.3) nous a appris que la distribution d’échantillonnage de la moyenne est approximativement normale. Nous savons également, d’après notre analyse de la distribution normale (section 7.5), qu’il y a 95 % de chances qu’une quantité normalement distribuée se situe à l’intérieur d’environ deux écarts-types de la moyenne réelle.
Pour être plus précis, la réponse la plus correcte est qu’il y a 95 % de chances qu’une quantité normalement distribuée se situe à l’intérieur de 1,96 écart type de la moyenne réelle. Ensuite, rappelez-vous que l’écart-type de la distribution d’échantillonnage est désigné sous le nom d’erreur-type, et que l’erreur-type de la moyenne est écrite sous le nom de SEM. Lorsque nous mettons tous ces éléments ensemble, nous apprenons qu’il y a une probabilité de 95 % que la moyenne de l’échantillon \(\bar{X}\) que nous avons effectivement observée se situe à l’intérieur de 1,96 erreur type de la moyenne de la population.
Mathématiquement, nous écrivons ceci comme :
\[ \mu - \left( 1,96*SEM \right) \leq \bar{X} \leq \mu + (1,96*SEM) \]
où le SEM est égal à \(\sigma/\sqrt{N}\) et nous pouvons être sûrs à 95% que c’est vrai. Cependant, cela ne répond pas à la question qui nous intéresse. L’équation ci-dessus nous indique ce à quoi nous devons nous attendre au sujet de la moyenne de l’échantillon étant donné que nous connaissons les paramètres de la population. Ce que nous voulons, c’est que ce travail se fasse dans l’autre sens. Nous voulons savoir ce que nous devons croire des paramètres de la population, étant donné que nous avons observé un échantillon particulier. Cependant, ce n’est pas trop difficile à faire. En utilisant un peu d’algèbre de lycée, une façon sournoise de réécrire notre équation est comme ceci :
\[ \bar{X} - \left( 1,96*SEM \right) \leq \mu \bar{X} + (1,96*SEM) \]
Ce qui est révélateur, c’est que la plage de valeurs a une probabilité de 95 % de contenir la moyenne de la population µ. Nous appelons cette plage un intervalle de confiance à 95 %, appelé CI95. Bref, tant que N est suffisamment grand (assez grand pour que l’on croie que la distribution d’échantillonnage de la moyenne est normale), nous pouvons écrire cette formule comme étant notre formule pour l’intervalle de confiance à 95 % :
\[ \text{CI}_{95}=\bar{X}\pm \left ( 1,96\times\frac{\sigma}{\sqrt{N}} \right ) \]
Bien sûr, il n’y a rien de spécial avec le chiffre 1,96. C’est tout simplement le multiplicateur qu’il vous faut utiliser si vous voulez un intervalle de confiance à 95 %. Si j’avais voulu un intervalle de confiance de 70%, j’aurais utilisé 1,04 comme chiffre magique plutôt que 1,96.
8.5.1 Une légère erreur dans la formule
Comme d’habitude, j’ai menti. La formule que j’ai donnée ci-dessus pour l’intervalle de confiance à 95 % est à peu près exacte, mais j’ai passé sous silence un détail important de la discussion. Notez que ma formule exige que vous utilisiez l’erreur type de la moyenne, SEM, ce qui vous oblige à utiliser l’écart-type de la population réelle \(\sigma\). Pourtant, à la section 8.4, j’ai souligné le fait que nous ne connaissons pas réellement les vrais paramètres de population. Comme nous ne connaissons pas la valeur réelle de \(\sigma\), nous devons plutôt utiliser une estimation de l’écart-type de la population (\(\hat{\sigma}\)). C’est assez simple à faire, mais cela a pour conséquence que nous devons utiliser les percentiles de la distribution t plutôt que la distribution normale pour calculer notre nombre magique, et la réponse dépend de la taille de l’échantillon. Quand N est très grand, on obtient à peu près la même valeur en utilisant la distribution t ou la distribution normale : 1,96. Mais lorsque N est petit, nous obtenons un nombre beaucoup plus grand lorsque nous utilisons la distribution t : 2,26.
Il n’y a rien de trop mystérieux dans ce qui se passe ici. Des valeurs plus élevées signifient que l’intervalle de confiance est plus large, ce qui indique que nous sommes plus incertains quant à la valeur réelle de µ. Lorsque nous utilisons la distribution t au lieu de la distribution normale, nous obtenons des nombres plus grands, ce qui indique que nous avons plus d’incertitude. Et pourquoi avons-nous cette incertitude supplémentaire ? Eh bien, parce que notre estimation de l’écart-type de la population \(\hat{\sigma}\) pourrait être fausse ! Si c’est faux, cela signifie que nous sommes un peu moins sûrs de ce à quoi ressemble réellement notre distribution d’échantillonnage de la moyenne, et cette incertitude finit par se refléter dans un intervalle de confiance plus large.
8.5.2 Interpréter un intervalle de confiance
Le plus difficile dans les intervalles de confiance, c’est de comprendre ce qu’ils signifient. Chaque fois que les gens rencontrent pour la première fois des intervalles de confiance, le premier instinct est presque toujours de dire « qu’il y a une probabilité de 95% que la vraie moyenne se trouve à l’intérieur de l’intervalle de confiance ». C’est simple et cela semble saisir l’idée de bon sens de ce que cela signifie de dire que je suis « confiant à 95% ». Malheureusement, ce n’est pas tout à fait juste. La définition intuitive repose en grande partie sur vos croyances personnelles quant à la valeur de la moyenne de la population. Je dis que je suis confiant à 95 p. 100 parce que ce sont mes croyances. Dans la vie de tous les jours, c’est tout à fait normal, mais si vous vous souvenez de la section 7.2, vous remarquerez que parler de croyances et de confiance personnelles est une idée bayésienne. Cependant, les intervalles de confiance ne sont pas des outils bayésiens. Comme tout le reste dans ce chapitre, les intervalles de confiance sont des outils fréquentistes, et si vous utilisez des méthodes fréquentistes, il n’est pas approprié de leur attacher une interprétation bayésienne. Si vous utilisez des méthodes fréquentistes, vous devez adopter des interprétations fréquentistes !
Bien, donc si ce n’est pas la bonne réponse, qu’est-ce que c’est ? Souvenez-vous de ce qu’on a dit à propos de la probabilité fréquentiste. La seule façon de parler de « probabilité » est de parler d’une séquence d’événements et de compter les fréquences des différents types d’événements. De ce point de vue, l’interprétation d’un intervalle de confiance à 95 % doit avoir quelque chose à voir avec la réplication. Plus précisément, si nous répétions l’expérience à maintes reprises et calculions un intervalle de confiance de 95 % pour chaque répétition, alors 95 % de ces intervalles contiendraient la vraie moyenne. De façon plus générale, 95 % de tous les intervalles de confiance construits à l’aide de cette procédure devraient contenir la moyenne réelle de la population. Cette idée est illustrée à la Figure 8‑12, qui montre 50 intervalles de confiance construits pour une expérience de « mesure de 10 QI » (figure supérieure) et 50 autres intervalles de confiance pour une expérience de « mesure de 25 QI » (figure inférieure). Un peu fortuitement, sur les 100 répétitions que j’ai simulées, il s’est avéré que 95 d’entre elles exactement contenaient la vraie moyenne.
La différence critique ici est que la revendication bayésienne parle de probabilité au sujet de la moyenne de la population (c.-à-d. qu’elle fait référence à notre incertitude au sujet de la moyenne de la population), ce qui n’est pas permis selon l’interprétation fréquentiste de la probabilité parce que vous ne pouvez « reproduire » une population ! Dans la le pont de vue fréquentiste, la moyenne de population est fixe et aucune affirmation probabiliste ne peut être faite à ce sujet. Les intervalles de confiance, cependant, sont reproductibles pour que nous puissions répéter les expériences. Par conséquent, un fréquentiste est autorisé à parler de la probabilité de l’intervalle de confiance contienne la vraie moyenne, mais il n’est pas permis de parler de la probabilité que la vraie moyenne de la population (qui n’est pas un événement répétable) se situe dans l’intervalle de confiance.
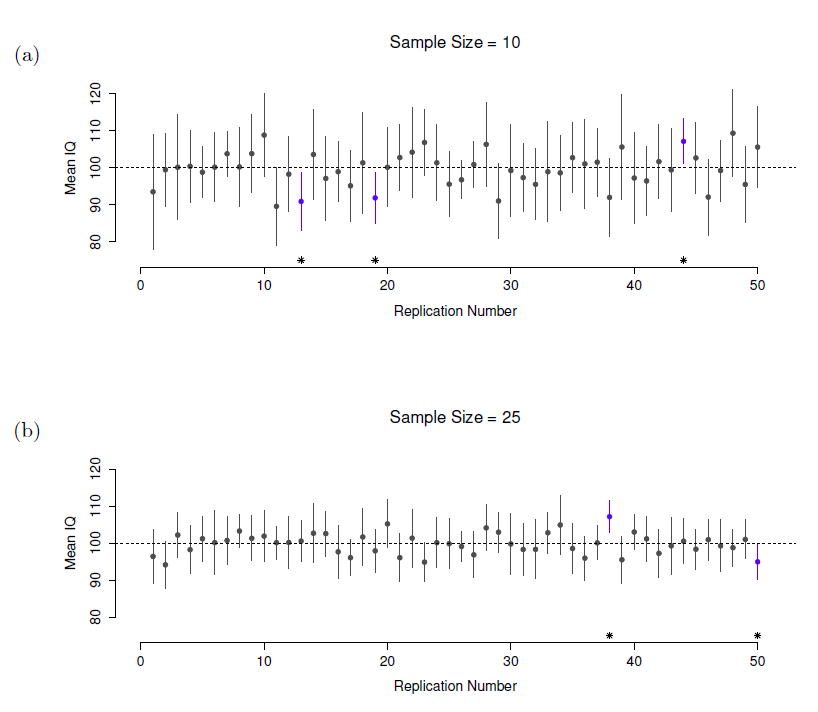
Figure 8‑12 Intervalles de confiance à 95 %. La partie supérieure (panneau a) montre 50 répétitions simulées d’une expérience dans laquelle nous mesurons les QI de 10 personnes. Le point marque l’emplacement de la moyenne de l’échantillon et la ligne indique l’intervalle de confiance à 95 %. Au total, 47 des 50 intervalles de confiance contiennent la vraie moyenne (c.-à-d. 100), mais pas les trois intervalles marqués d’un astérisque. Le graphique du bas (panneau b) montre une simulation similaire, mais cette fois nous simulons des réplications d’une expérience qui mesure les QI de 25 personnes.
Je sais que cela semble un peu pédant, mais c’est important. C’est important parce que la différence d’interprétation conduit à une différence mathématique. Il existe une alternative bayésienne aux intervalles de confiance, appelés intervalles crédibles. Dans la plupart des cas, les intervalles crédibles sont assez semblables aux intervalles de confiance, mais dans d’autres cas, ils sont très différents. Comme promis, cependant, je parlerai plus en détail de la perspective bayésienne au chapitre 15.
8.5.3 Calcul des intervalles de confiance dans Jamovi
Pour autant que je puisse le dire, Jamovi n’inclut pas (encore) de méthode simple pour calculer les intervalles de confiance de la moyenne dans le cadre de la fonctionnalité « Descriptives ». Mais les « Descriptives » ont une case à cocher pour la SEM., vous pouvez donc l’utiliser pour calculer l’intervalle de confiance inférieur de 95% comme :
Moyenne - (1,96 * SEM),
et l’intervalle de confiance supérieur à 95 % comme :
Moyenne + (1,96 * SEM)
Les intervalles de confiance à 95 % sont la norme de facto en psychologie. Ainsi, par exemple, si je charge le fichier IQsim.omv, vérifie la moyenne et SEM sous « Descriptives », je peux calculer l’intervalle de confiance associé au QI moyen simulé :
IC 95 % inférieur = 99,68 - (1,96 * 0,15) = 99,39 IC supérieur 95 % = 99,68 + (1,96 * 0,15) = 99,98
Ainsi, dans nos données simulées sur un grand échantillon avec N = 10 000, le QI moyen est de 99,68 avec un IC à 95 % de 99,39 à 99,98. J’espère que c’est assez clair. Ainsi, bien qu’il n’existe pas actuellement de moyen simple d’obtenir de Jamovi qu’il calcule l’intervalle de confiance dans le cadre des options de la variable « Descriptives », si nous le voulions, nous pourrions assez facilement le calculer à la main.
De même, lorsqu’il s’agit de tracer les intervalles de confiance dans Jamovi, cela n’est pas (encore) disponible dans le cadre des options « Descriptives ». Cependant, lorsque nous nous familiariserons avec des tests statistiques spécifiques, par exemple au chapitre 13, nous verrons que nous pouvons tracer des intervalles de confiance dans le cadre de l’analyse des données. C’est plutôt cool, on vous montrera alors comment faire cela plus tard.
8.6 Résumé
Dans ce chapitre, j’ai couvert deux sujets principaux. La première moitié du chapitre traite de la théorie de l’échantillonnage, et la seconde de la façon dont nous pouvons utiliser la théorie de l’échantillonnage pour construire des estimations des paramètres de la population. La répartition des sections ressemble à ceci :
- Idées de base sur les échantillons, l’échantillonnage et les populations (Section 8.1)
- Théorie statistique de l’échantillonnage : la loi des grands nombres (section 8.2), les distributions d’échantillonnage et le théorème de la limite centrale (section 8.3).
- Estimation des moyennes et des écarts-types (section 8.4)
- Estimation d’un intervalle de confiance (section 8.5)
Comme toujours, il y a beaucoup de sujets liés à l’échantillonnage et à l’estimation qui ne sont pas abordés dans ce chapitre, mais pour un cours d’introduction à la psychologie, c’est assez complet je pense. Pour la plupart des chercheurs appliqués, vous n’aurez pas besoin de beaucoup plus de théorie que cela. Une grande question que je n’ai pas abordée dans ce chapitre est ce que vous faites quand vous n’avez pas un échantillon aléatoire simple. Il y a beaucoup de théorie statistique sur laquelle on peut s’appuyer pour gérer cette situation, mais cela dépasse largement le cadre de ce livre.
References
Keynes, John Maynard. 2009. A Tract on Monetary Reform. Place of publication not identified: WWW.Therichestmaninbabylon.Org.
Stigler, Sm. 1986. The History of Statistics the Measurement of Uncertainty Before 1900. Reprint. Cambridge, Mass.: Harvard University Press.
La définition mathématique correcte du hasard est extraordinairement technique et dépasse largement le cadre de ce livre. Nous ne serons pas techniques ici et dirons qu’un processus comporte un élément de hasard chaque fois qu’il est possible de répéter le processus et d’obtenir des réponses différentes à chaque fois.↩︎
Rien dans la vie n’est aussi simple. Il n’y a pas une division évidente des gens en catégories binaires comme “schizophrène” et “pas schizophrène”. Mais ce n’est pas un texte de psychologie clinique, alors pardonnez-moi quelques simplifications ici et là.↩︎
Techniquement, la loi des grands nombres s’applique à tout échantillon statistique qui peut être décrit comme une moyenne de quantités indépendantes. C’est certainement vrai pour la moyenne de l’échantillon. Cependant, il est également possible d’écrire beaucoup d’autres exemples de statistiques sous forme de moyennes d’une forme ou d’une autre. La variance d’un échantillon, par exemple, peut être réécrite comme une sorte de moyenne et est donc soumise à la loi des grands nombres. La valeur minimale d’un échantillon, cependant, ne peut pas être écrite comme une moyenne de quoi que ce soit et n’est donc pas régie par la loi des grands nombres.↩︎
Comme d’habitude, je suis un peu négligent. Le théorème de la limite centrale est un peu plus général que ne l’implique cette section. Comme la plupart des textes d’introduction aux statistiques, j’ai discuté d’une situation où le théorème de la limite centrale s’applique : lorsque vous prenez une moyenne sur un grand nombre d’événements indépendants tirés de la même distribution. Cependant, le théorème de la limite centrale est beaucoup plus large que cela. Il y a toute une classe de choses appelées “U-statistiques” par exemple, qui satisfont toutes le théorème de la limite centrale et sont donc normalement distribuées pour les échantillons de grande taille. La moyenne est l’une de ces statistiques, mais ce n’est pas la seule.↩︎
Veuillez noter que si cette question vous intéressait vraiment, vous devriez être beaucoup plus prudent que moi. Vous ne pouvez pas simplement comparer les scores de QI de Whyalla à Port Pirie et supposer que les différences sont dues au saturnisme. Même s’il est vrai que les seules différences entre les deux villes correspondaient à des raffineries différentes (et ce n’est pas le cas, loin s’en faut), il faut tenir compte du fait que les gens croient déjà que la pollution au plomb provoque des déficits cognitifs. Si vous vous rappelez le chapitre 2, cela signifie qu’il y a des effets de demande différents pour l’échantillon de Port Pirie et pour celui de Whyalla. En d’autres termes, vous pourriez vous retrouver avec une différence de groupe illusoire dans vos données, causée par le fait que les gens pensent qu’il y a une différence réelle. Je trouve peu plausible de penser que les habitants de Port Pirie ne seraient pas bien au courant de ce que vous essayez de faire si un groupe de chercheurs se présentait à Port Pirie avec des blouses de laboratoire et des tests de QI, et encore moins plausible de penser que beaucoup de gens vous en voudraient beaucoup de le faire. Ces gens ne seront pas aussi coopératifs dans les tests. D’autres personnes à Port Pirie pourraient être plus motivées à réussir parce qu’elles ne veulent pas que leur ville natale ait mauvaise mine. Les effets de motivation qui s’appliqueraient dans Whyalla sont susceptibles d’être plus faibles, parce que les gens n’ont pas de concept « d’intoxication au minerai de fer » de la même manière qu’ils ont un concept « d’intoxication au plomb ». La psychologie est difficile.↩︎
Je dois noter que je cache quelque chose ici. L’impartialité est une caractéristique souhaitable pour un estimateur, mais il y a d’autres choses qui comptent en plus du biais. Cependant, ce n’est pas l’objet de ce livre d’en discuter en détail. Je veux simplement attirer votre attention sur le fait qu’il y a là une certaine complexité cachée.↩︎
D’accord, je cache quelque chose d’autre ici. De façon bizarre et contre-intuitive, puisque \(\hat{\sigma}^{2}\) est un estimateur non biaisé de \(\sigma^{2}\), on pourrait supposer que prendre la racine carrée serait bien et que \(\hat{\sigma}\) serait un estimateur non biaisé de \(\sigma\). Bizarrement, ça ne l’est pas. Il y a en fait un biais subtil et minuscule dans \(\hat{\sigma}\). C’est tout simplement bizarre : \({\hat{\sigma}}^{2}\) est une estimation non biaisée de la variance de la population \(\sigma^{2}\), mais lorsque vous prenez la racine carrée, il s’avère que \(\hat{\sigma}\). est un estimateur biaisé de l’écart-type de la population \(\sigma\). Bizarre, bizarre, bizarre, pas vrai ? Alors, pourquoi \(\hat{\sigma}\). est-il biaisé ? La réponse technique est « parce que les transformations non linéaires (par exemple, la racine carrée) ne correspondent pas aux attentes », mais cela ressemble à du charabia pour tous ceux qui n’ont pas suivi de cours en statistique mathématique. Heureusement, cela n’a pas d’importance en pratique. Le biais est faible, et dans la vraie vie tout le monde utilise \(\hat{\sigma}\). et ça marche très bien. Parfois, les mathématiques sont tout simplement ennuyeuses.↩︎
Cette citation apparaît sur un grand nombre de t-shirts et de sites web, et est même mentionnée dans quelques articles académiques.(voir http://www. mais je n’ai jamais trouvé la source originale.↩︎