Chapitre 15 Analyse factorielle
Les chapitres précédents ont couvert les tests statistiques visant à déterminer les différences entre deux groupes ou plus. Cependant, dans le cadre d’une recherche, il nous arrive parfois de vouloir examiner la covariabilité de variables multiples. C’est-à-dire, la façon dont elles sont reliées les unes aux autres et de voir si les schémas de relation nous suggèrent quelque chose d’intéressant et ayant dus sens. Par exemple, nous sommes souvent intéressés à déterminer l’existence de facteurs latents sous-jacents à partir des variables observées et mesurées directement dans notre ensemble de données. En statistique, les facteurs latents sont des variables cachées qui ne sont pas directement observées, mais plutôt déduites (par analyse statistique) d’autres variables qui sont observées (mesurées directement).
Dans ce chapitre, nous examinerons un certain nombre d’analyses factorielles et de techniques connexes, en commençant par l’analyse factorielle exploratoire ou AFE (en anglais : Exploratory factorial analysis ou EFA). L’AFE est une technique statistique permettant d’identifier les facteurs latents sous-jacents dans un ensemble de données (section 15.1). Ensuite, dans la section 15.2, nous aborderons l’analyse en composantes principales (ACP) qui est une technique de réduction des données qui, à proprement parler, ne permet pas d’identifier les facteurs latents sous-jacents. Au lieu de cela, l’ACP produit simplement une combinaison linéaire de variables observées. Ensuite, la section 15.3 sur l’analyse factorielle confirmatoire (AFC) montre que, contrairement à l’AFE, avec l’AFC, vous commencez par une idée - un modèle - de la façon dont les variables de vos données sont reliées les unes aux autres. Vous testez ensuite votre modèle par rapport aux données observées et évaluez dans quelle mesure il s’adapte au modèle. Une version plus sophistiquée de l’AFC est l’approche dite Multi-Trait Multi-Method (MTMM) (section 15.4), dans laquelle le modèle tient compte à la fois de la variance latente du facteur et de la méthode. Ceci est utile lorsqu’il existe différentes approches méthodologiques utilisées pour la collecte des données et que la variabilité de la méthodologie est donc une question importante. Enfin, nous aborderons une analyse connexe : l’analyse de fiabilité de la cohérence interne teste la cohérence d’une échelle pour la mesure une construction psychologique (section 15.5).
15.1 Analyse factorielle exploratoire
L’analyse factorielle exploratoire (AFE) est une technique statistique permettant de révéler tous les facteurs latents cachés qui peuvent être déduits de nos données observées. Cette technique calcule dans quelle mesure un ensemble de variables mesurées, par exemple V1, V2, V3, V4 et V5, peut être représenté comme mesures d’un facteur latent sous-jacent. Ce facteur latent ne peut pas être mesuré au moyen d’une seule variable observée, mais il se manifeste plutôt par les relations qu’il provoque dans un ensemble de variables observées.
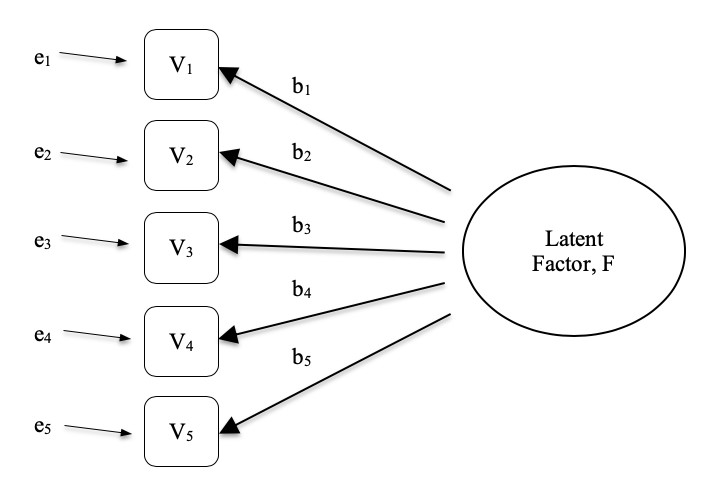
Dans la Figure 15‑1, chaque variable observée V est « causée « dans une certaine mesure par le facteur latent sous-jacent (F), représenté par les coefficients b1 à b5 (aussi appelés saturations de facteurs). Chaque variable observée a également un terme d’erreur associé, e1 à e5. Chaque terme d’erreur est la variance de la variable observée associée, Vi, qui est inexpliquée par le facteur latent sous-jacent.
Figure 15‑1 : Facteur latent sous-jacent à la relation entre plusieurs variables observées
En psychologie, les facteurs latents représentent des phénomènes ou des constructions psychologiques difficiles à observer ou à mesurer directement. Par exemple, la personnalité, l’intelligence ou le style de pensée. Dans l’exemple de la Figure 15‑1, nous avons peut-être posé cinq questions précises sur le comportement ou les attitudes des gens, ce qui nous permet de nous faire une idée d’un concept de personnalité appelé, par exemple, extraversion. Un ensemble différent de questions spécifiques peut nous donner une image de l’introversion d’un individu, ou de sa conscience. Et ces différents facteurs latents peuvent être corrélés entre eux.
Voici un autre exemple : nous pouvons ne pas être en mesure de mesurer directement l’anxiété liée aux statistiques, mais nous pouvons mesurer si l’anxiété liée aux statistiques est élevée ou faible avec un ensemble d’items dans un questionnaire. Par exemple, « Q1 : Faire le devoir d’un cours de statistique », « Q2 : Essayer de comprendre les statistiques décrites dans un article de journal », et « Q3 : Demander à l’enseignant de l’aider à comprendre quelque chose du cours », etc. Les personnes ayant une grande anxiété statistique auront aussi tendance à donner des réponses élevées à ces variables en raison de leur anxiété statistique importante. De même, les personnes dont l’anxiété statistique est faible donneront de la même façon des réponses faibles à ces variables en raison de leur faible anxiété statistique.
Dans l’analyse factorielle exploratoire (AEF), nous explorons essentiellement les corrélations entre les variables observées pour découvrir tout facteur sous-jacent (latent) intéressant et important qui est identifié lorsque les variables observées covarient. Nous pouvons utiliser un logiciel statistique pour estimer tout facteur latent et pour identifier les variables qui ont une saturation importante136 (p. ex., saturation > 0,5) sur chaque facteur, ce qui suggère qu’elles sont une mesure ou un indicateur utile du facteur latent. Une partie de ce processus comprend une étape appelée rotation, ce qui pour être honnête est une idée assez bizarre, mais heureusement nous n’avons pas à nous soucier de la comprendre ; nous avons juste besoin de savoir qu’elle est utile parce qu’elle rend beaucoup plus clair le modèle des saturations sur différents facteurs. Ainsi, la rotation aide à mieux voir quelles variables sont liées de façon substantielle à chaque facteur. Nous devons également décider combien de facteurs sont raisonnables compte tenu de nos données, et ce qui est utile à cet égard, ce sont les valeurs propres qui indiquent l’ampleur de chaque facteur.
15.1.1 Vérification des hypothèses
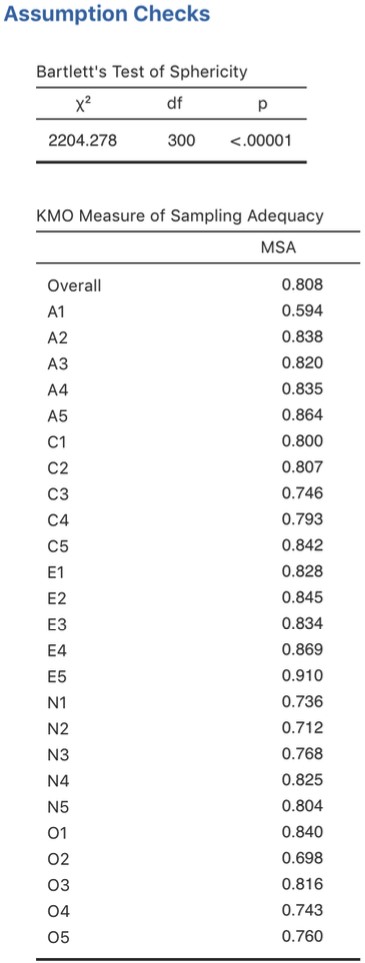
Il y a aussi quelques hypothèses qui doivent être vérifiées dans le cadre de cette analyse. La première hypothèse est la sphéricité, qui vérifie essentiellement que les variables de votre ensemble de données sont suffisamment corrélées entre elles pour être résumées avec un ensemble plus restreint de facteurs. Le test de sphéricité de Bartlett vérifie si la matrice de corrélation observée s’écarte significativement d’une matrice à corrélation nulle. Ainsi, si le test de Bartlett est significatif (p<.05), cela indique que la matrice de corrélation observée est significativement divergente de la matrice nulle, et donc convient à l’AFE.
La deuxième hypothèse est l’adéquation de l’échantillonnage et est vérifiée à l’aide de la mesure de l’adéquation de l’échantillonnage (Measure of sampling adequation ou MSA) de Kaiser-Meyer-Olkin (KMO). L’indice KMO est une mesure de la proportion de variance parmi les variables observées qui pourrait être une variance commune. Il vérifie les corrélations partielles, c’est-à-dire lorsqu’il y a des facteurs qui ne saturent que deux éléments. Nous voulons rarement, sinon jamais, que l’AFE produise beaucoup de facteurs en ne saturant que deux éléments chacun. Le KMO concerne l’adéquation de l’échantillonnage car des corrélations partielles sont généralement observées avec des échantillons inadéquats. Si l’indice KMO est élevé (\(\approx 1\)), le CFC est efficace alors que si le KMO est faible (\(\approx 0\)), l’AFE n’est pas pertinente. Des valeurs KMO inférieures à 0,5 indiquent que l’AFE n’est pas appropriée et une valeur KMO de 0,6 devrait être confirmée avant que l’AFE soit considérée comme appropriée. Les valeurs entre 0,5 et 0,7 sont considérées comme adéquates, les valeurs entre 0,7 et 0,9 sont bonnes et les valeurs entre 0,9 et 1,0 sont excellentes.
15.1.2 A quoi sert l’AFE ?
Si l’AFE a fourni une bonne solution (c.-à-d. un modèle factoriel), nous devons alors décider quoi faire de nos nouveaux facteurs. Les chercheurs utilisent souvent l’AFE au cours de l’élaboration de l’échelle psychométrique. Ils développeront l’ensemble des items d’un questionnaire qui, selon eux, se rapportent à une ou plusieurs constructions psychologiques, utiliseront l’AFE pour voir quels items « vont ensemble » comme facteurs latents, puis ils évalueront si certains items devraient être supprimés parce qu’ils ne mesurent pas de façon utile ou distincte un des facteurs latents.
Conformément à cette approche, une autre conséquence de l’AFE est de combiner les variables qui saturent des facteurs distincts à travers un score factoriel, parfois appelé score gradué. Il y a deux options pour combiner des variables dans une échelle de notation :
- Créez une nouvelle variable avec une note pondérée par les coefficients de pondération pour chaque élément qui sature un facteur.
- Créez une nouvelle variable en fonction de chaque élément qui sature un facteur, mais en les pondérant également.
Dans la première option, la saturation de chaque élément au score combiné dépend de l’importance de son lien avec le facteur. Dans la deuxième option, nous faisons généralement la moyenne de tous les éléments qui saturent de façon substantielle un facteur pour créer la variable de l’échelle de notation combinée. Le choix est une question de préférence, bien que la première présente l’inconvénient que les saturations peuvent varier considérablement d’un échantillon à l’autre, surtout dans les sciences du comportement et de la santé, où nous sommes souvent intéressés à développer et à utiliser des échelles construites sur des questionnaires composites pour différentes études et différents échantillons. Dans ce cas, il est raisonnable d’utiliser une mesure composite fondée sur la saturation égale des éléments de fond plutôt que sur la pondération par les saturations spécifiques d’un échantillon provenant d’un échantillon différent. Dans tous les cas, il est plus simple et plus intuitif de comprendre une mesure de variable combinée comme une moyenne d’éléments que d’utiliser une combinaison pondérée de façon optimale spécifique à un échantillon.
Une technique statistique plus avancée, qui dépasse la portée du présent ouvrage, consiste à entreprendre une modélisation de régression où les facteurs latents sont utilisés dans les modèles de prédiction d’autres facteurs latents. C’est ce qu’on appelle la « modélisation d’équation structurelle » et il existe des logiciels et des progiciels R spécifiques dédiés à cette approche. Mais n’allons pas trop vite ; ce sur quoi nous devrions vraiment nous concentrer maintenant, c’est sur la manière de faire une AFE avec Jamovi.
15.1.3 Faire une AFE avec Jamovi
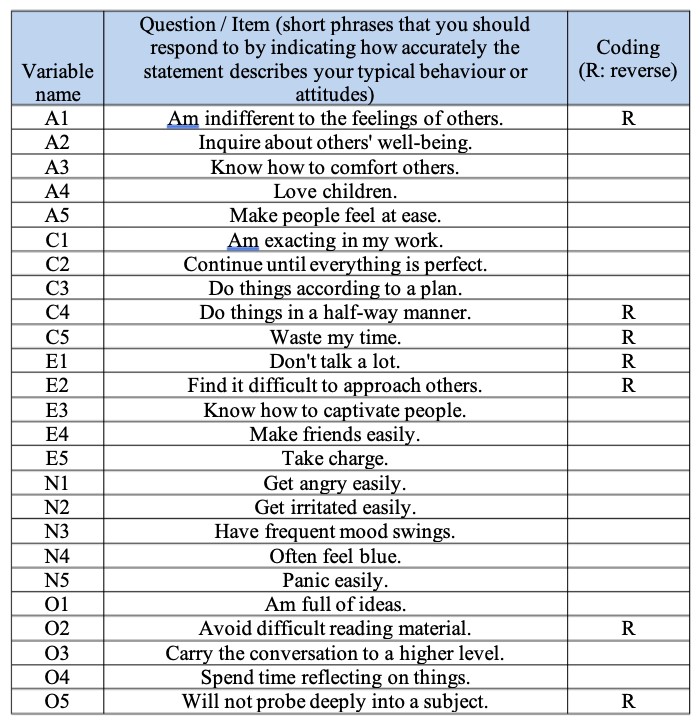
D’abord, il nous faut des données. Vingt-cinq éléments d’auto-évaluation de la personnalité (voir Figure 15‑2) tirés de l’International Personality Item Pool () ont été inclus dans le cadre du projet SAPA (Synthetic Aperture Personality Assessment) sur le Web (SAPA : .) Les 25 items sont organisés selon cinq facteurs présumés : Agréabilité, Conscience, Extraversion, Névrose et Ouverture.
Figure 15‑2 : Vingt-cinq items variables observés organisés selon cinq facteurs de personnalité présumés dans l’ensemble de donnéesbfi_sample.csv
Les données sur les items ont été recueillies à l’aide d’une échelle de réponse en 6 points :
- Très imprécis
- Modérément inexact
- Légèrement inexact
- Légèrement précis
- Modérément précis
- Très précis.
Un échantillon de N=250 réponses est contenu dans l’ensemble de données bfi_sample.csv. En tant que chercheurs, nous souhaitons explorer les données pour voir s’il existe des facteurs latents sous-jacents qui sont raisonnablement bien mesurés par les 25 variables observées dans le fichier de données bfi_sample.csv. Ouvrez l’ensemble de données et vérifiez que les 25 variables sont codées en tant que variables continues (on peut soutenir qu’elles sont ordinales mais pour l’AFE dans Jamovi, cela n’a généralement pas d’importance, sauf si vous décidez de calculer des scores factoriels pondérés, auquel cas des variables continues sont nécessaires). Pour réaliser l’AFE avec Jamovi :
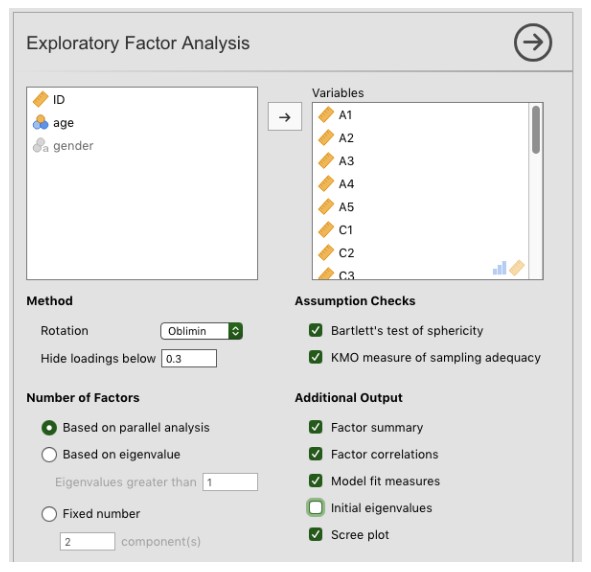
Sélectionnez Factor - Exploratory Factor Analysis dans la barre principale de boutons de Jamovi pour ouvrir la fenêtre d’analyse de l’AFE (Figure 15‑3).
Sélectionnez les 25 questions de personnalité et transférez-les dans la boîte’Variables’.
Cochez les options appropriées, y compris les options « Assumptions checks », mais aussi « ’Method » de rotation, « Number of Factors to extract » et « Additional Output ». Voir la Figure 15‑3 pour les options suggérées pour cet exemple d’AFE, et notez que la méthode de rotation et le nombre de facteurs à extraire sont habituellement ajustés pendant l’analyse pour trouver le meilleur résultat, tel que décrit ci-dessous.
Figure 15‑3 : La fenêtre d’analyse de l’AFE de Jamovi
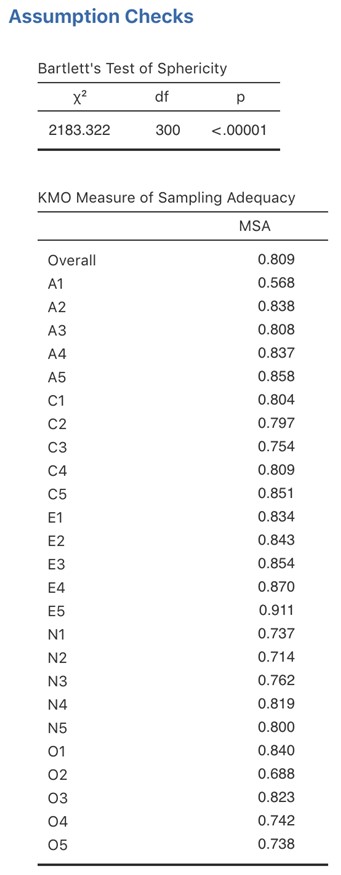
Tout d’abord, vérifions les hypothèses (Figure 15‑4). Vous pouvez voir que (1) le test de sphéricité de Bartlett est significatif, donc ce présupposé est satisfait ; et (2) la mesure de l’adéquation de l’échantillonnage (MSA) du KMO est globalement de 0,81, ce qui suggère une bonne adéquation d’échantillonnage. Nous n’avons pas de problème dans ce cas !
Figure 15‑4 : Vérification des hypothèse de l’AFE dans Jamovi pour les données du questionnaire de personnalité
Il faut vérifier ensuite le nombre de facteurs à utiliser (ou « extraits » des données). Trois approches différentes sont disponibles :
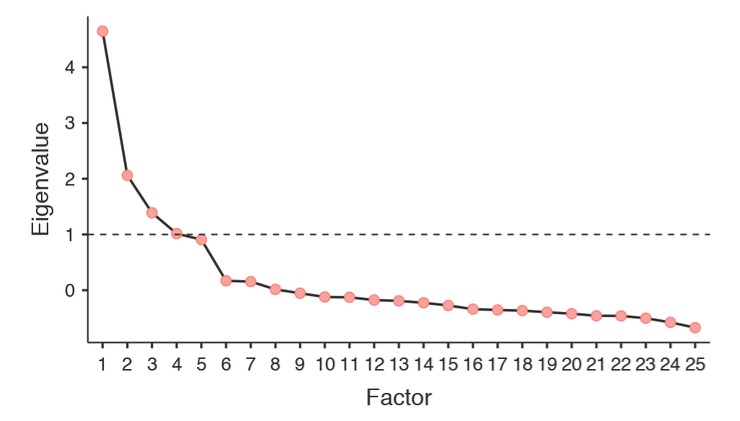
Une convention consiste à choisir tous les composants dont les valeurs propres (Eigenvalue) sont supérieures à 1137. Cela nous donnerait quatre facteurs avec nos données (essayez pour voir).
L’examen de l’éboulis, comme sur la Figure 15‑5, permet d’identifier le « point d’inflexion ». C’est le point où la pente de la courbe de l’éboulis se stabilise nettement en dessous du « coude ». Cela nous donnerait cinq facteurs avec nos données. L’interprétation des tracés d’éboulis est un peu un art : dans la Figure 15‑5, il y a un saut notable de 5 à 6 facteurs, mais dans d’autres tracés d’éboulis, on ne peut pas voir une coupe aussi nette.
En utilisant une technique d’analyse parallèle, les valeurs propres obtenues sont comparées à celles qui seraient obtenues à partir de données aléatoires. Le nombre de facteurs extraits est le nombre de facteurs dont les valeurs propres sont supérieures à celles que l’on trouverait avec des données aléatoires.
Figure 15‑5 : Courbe de l’éboulis de l’EFA avec Jamovi sur les données de personnalité, montrant une inflexion perceptible et une stabilisation après le point 5 (le « coude »)
La troisième approche est satisfaisante selon Fabrigar, Wegener, MacCallum et Strahan (1999) considèrent qu’en pratique, les chercheurs ont tendance à examiner les trois critères précédents et à porter un jugement sur le nombre de facteurs qui sont les plus faciles ou utiles à interpréter. Cela peut être compris comme un « critère de pertinence », et les chercheurs examinent généralement, en plus de la solution de l’une des approches ci-dessus, des solutions comportant un ou deux facteurs plus ou moins importants. Ils adoptent ensuite la solution qui leur semble la plus logique.
Dans le même temps, nous devrions également réfléchir à la meilleure façon d’assurer la rotation de la solution finale. Il existe deux approches principales de la rotation : la rotation orthogonale (p. ex. « varimax ») force les facteurs sélectionnés à ne pas être corrélés, tandis que la rotation oblique (p. ex. « oblimin ») permet la corrélation des facteurs sélectionnés. Les dimensions qui intéressent les psychologues et les spécialistes du comportement ne sont pas souvent des dimensions que l’on s’attendrait à trouver orthogonales, de sorte que les solutions obliques sont sans doute plus raisonnables.
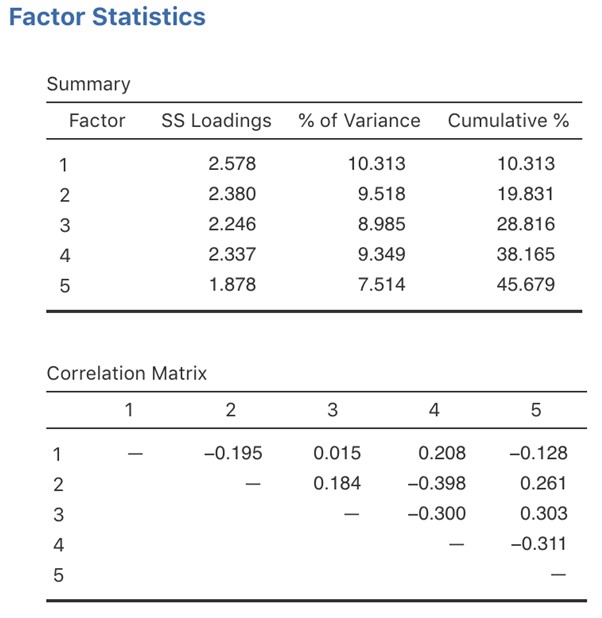
En pratique, si dans une rotation oblique, les facteurs sont substantiellement corrélés (positifs ou négatifs, et > 0.3), comme dans la Figure 15‑6 où une corrélation entre deux des facteurs extraits est -0,398, alors cela confirmerait notre intuition de préférer une rotation oblique. Si les facteurs sont, en fait, corrélés, alors une rotation oblique produira une meilleure estimation des vrais facteurs et une meilleure structure simple qu’une rotation orthogonale. Et, si la rotation oblique indique que les facteurs ont des corrélations proches de zéro entre eux, alors le chercheur peut procéder à une rotation orthogonale (qui devrait alors donner la même solution que la rotation oblique).
Figure 15‑6 : Résumés statistiques des facteurs et corrélations pour une solution à cinq facteurs de l’AFE dans Jamovi
En vérifiant la corrélation entre les facteurs extraits, au moins une corrélation était supérieure à 0,3 (Figure 15‑6), de sorte qu’une rotation oblique (oblimin) des cinq facteurs extraits est préférable. Nous pouvons également voir à la Figure 15‑6 que la proportion de la variance globale des données attribuable aux cinq facteurs est de 46 %. Le facteur un représente environ 10 % de la variance, les facteurs deux à quatre environ 9 % chacun et le facteur cinq un peu plus de 7 %. Ce n’est pas génial ; il aurait été préférable que la solution globale représente une proportion plus importante de l’écart dans nos données.
Sachez que dans chaque AFE, vous pouvez avoir le même nombre de facteurs que les variables observées, mais chaque facteur supplémentaire que vous incluez ajoutera une variance expliquée plus faible. Si les premiers facteurs expliquent une bonne partie de la variance des 25 variables initiales, alors ces facteurs sont clairement un substitut utile et plus simple aux 25 variables. Vous pouvez laisser tomber le reste sans perdre trop de la variabilité d’origine. Mais s’il faut 18 facteurs (par exemple) pour expliquer la majeure partie de la variance de ces 25 variables, autant utiliser les 25 variables initiales.
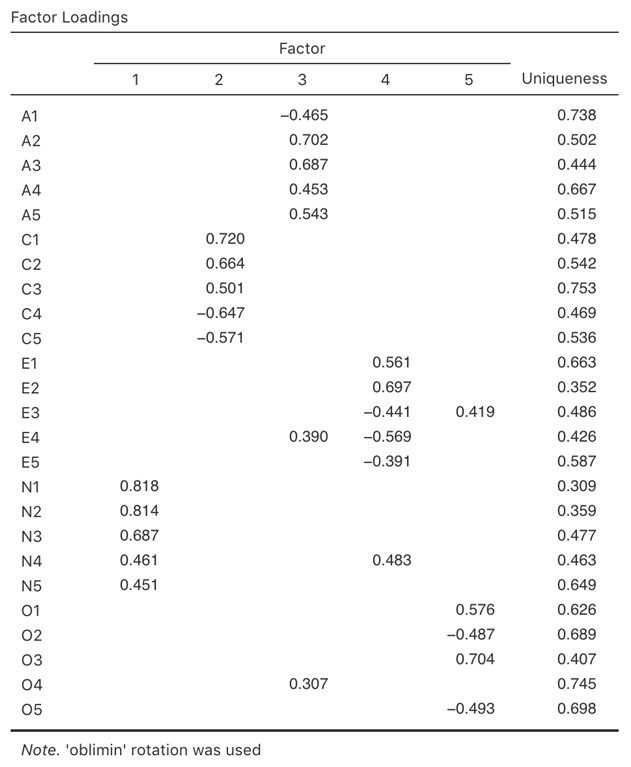
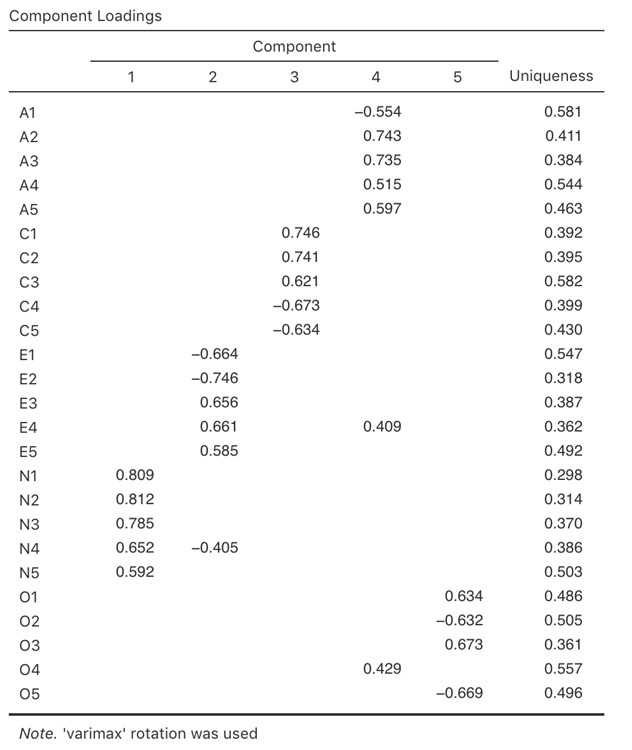
La Figure 15‑7 montre les conributions factorielles. C’est-à-dire, comment les 25 éléments de personnalité différents s’appliquent à chacun des cinq facteurs sélectionnés. Nous avons des saturations cachées inférieures à 0,3 (définies dans les options de la Figure 15‑3.
Pour les facteurs 1, 2, 3 et 4, le profil des saturations factorielles correspond étroitement aux facteurs présumés indiqués à la Figure 15‑2. Ouf ! Et le facteur 5 est assez proche, avec quatre des cinq variables observées qui mesurent supposément « l’ouverture » se chargeant assez bien sur le facteur. La variable 04 ne semble pas tout à fait convenir, car la solution factorielle de la Figure 15‑7 suggère qu’elle correle le facteur 3 (quoiqu’avec une corrélation relativement faible) mais pas substantiellement au facteur 5.
Il faut noter également que les variables qui ont été notées « R : codage inversé » à la Figure 15‑2 sont celles qui ont des saturations de facteurs négatives. Jetez un coup d’œil aux rubriques A1 (« Je suis indifférent aux sentiments des autres ») et A2 (« Se renseigner sur le bien-être des autres »). Nous pouvons voir qu’un score élevé sur A1 indique un faible degré d’agréabilité, alors qu’un score élevé sur A2 (et toutes les autres variables « A » d’ailleurs) indique un degré d’agréabilité élevé. Par conséquent, A1 sera corrélée négativement avec les autres variables « A », et c’est pourquoi il a une corrélation négative au facteur, comme le montre la Figure 15‑7.
Figure 15‑7 : Charges factorielles pour une solution à cinq facteurs dans l’EPT de Jamovi
On peut également voir dans la Figure 15‑7 « l’unicité »138 de chaque variable(uniqueness). L’unicité est la proportion de variance qui est « spécifique » à la variable et qui n’est pas expliquée par les facteurs139. Par exemple, 74 % de la variance de « A1 » ne s’explique pas par les facteurs de la solution à cinq facteurs. Par contre, la variance de « N1 » est relativement faible et n’est pas prise en compte par la solution factorielle (31 %). Il est à noter que plus l’unicité est grande, plus la pertinence ou la saturation de la variable dans le modèle factoriel est faible.
Pour être honnête, il est inhabituel d’obtenir une solution aussi soignée en matière d’AFE. C’est généralement un peu plus compliqué que cela, et souvent l’interprétation de la signification des facteurs est plus difficile. Ce n’est pas souvent que vous avez un ensemble d’éléments aussi bien défini. Le plus souvent, vous aurez tout un tas de variables observées qui, selon vous, peuvent être des indicateurs de facteurs latents, mais vous n’avez pas une idée aussi précise des variables qui y sont associées !
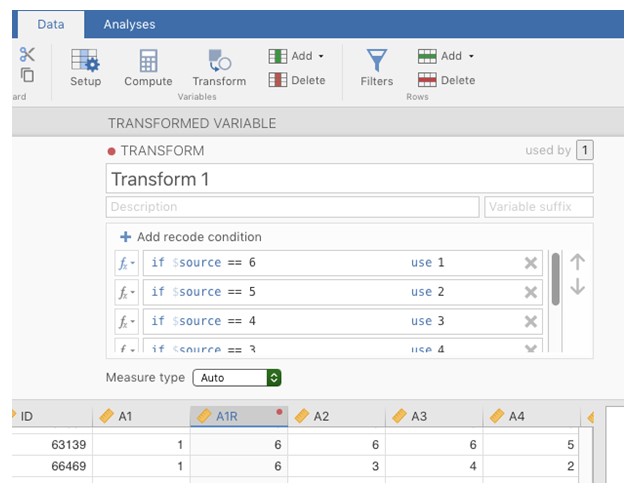
Figure 15‑8 : Variable de recodage à l’aide de la commande Jamovi « Transform »
Il semble donc que nous ayons une assez bonne solution à cinq facteurs. Supposons que nous soyons satisfaits de cette solution et que nous souhaitions utiliser nos facteurs dans une analyse plus approfondie. L’option simple consiste à calculer un score moyen pour chaque facteur en additionnant le score de chaque variable qui contribue de manière substantielle au facteur et à diviser ensuite par le nombre de variables. Pour chaque personne de notre ensemble de données, cela signifierait, par exemple pour le facteur d’agréabilité, additionner A1 + A2 + A3 + A4 + A5, puis diviser par 5, ce qui signifie que le score factoriel que nous avons calculé est basé sur des scores également pondérés pour chaque variable. On peut le faire avec Jamovi en deux étapes :
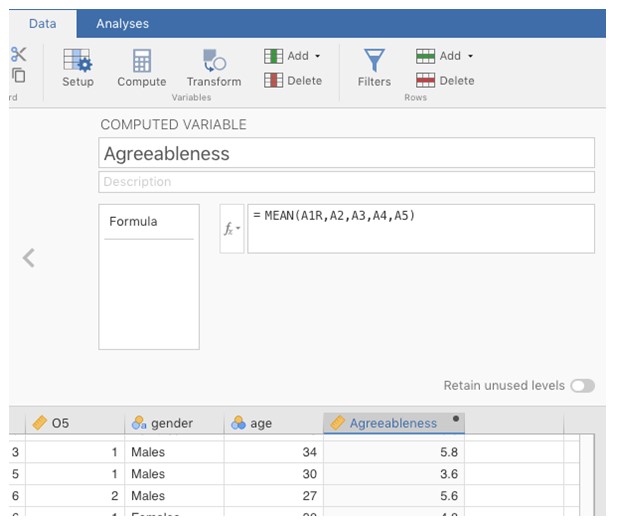
Recoder A1 en « A1R » en inversant les valeurs de la variable (i.e. 6 = 1; 5 = 2; 4 = 3; 3 = 4; 2 = 5; 1 = 6) en utilisant la commande de transformation de variable de Jamovi (voir Figure 15‑8).
Calculez une nouvelle variable, appelée « Agreeableness », en calculant la moyenne de A1R, A2, A3, A4 et A5. Pour ce faire, utilisez la commande de calcul de nouvelle variable de Jamovi (voir Figure 15‑9).
Figure 15‑9 : Calcul d’une nouvelle variable score factoriel à l’aide de la commande de Jamovi « Computed variable »
Une autre option consiste à créer un indice de score factoriel pondéré de façon optimale. Nous pouvons utiliser l’éditeur Rj de Jamovi pour le faire dans R. Encore une fois, il y a deux étapes :
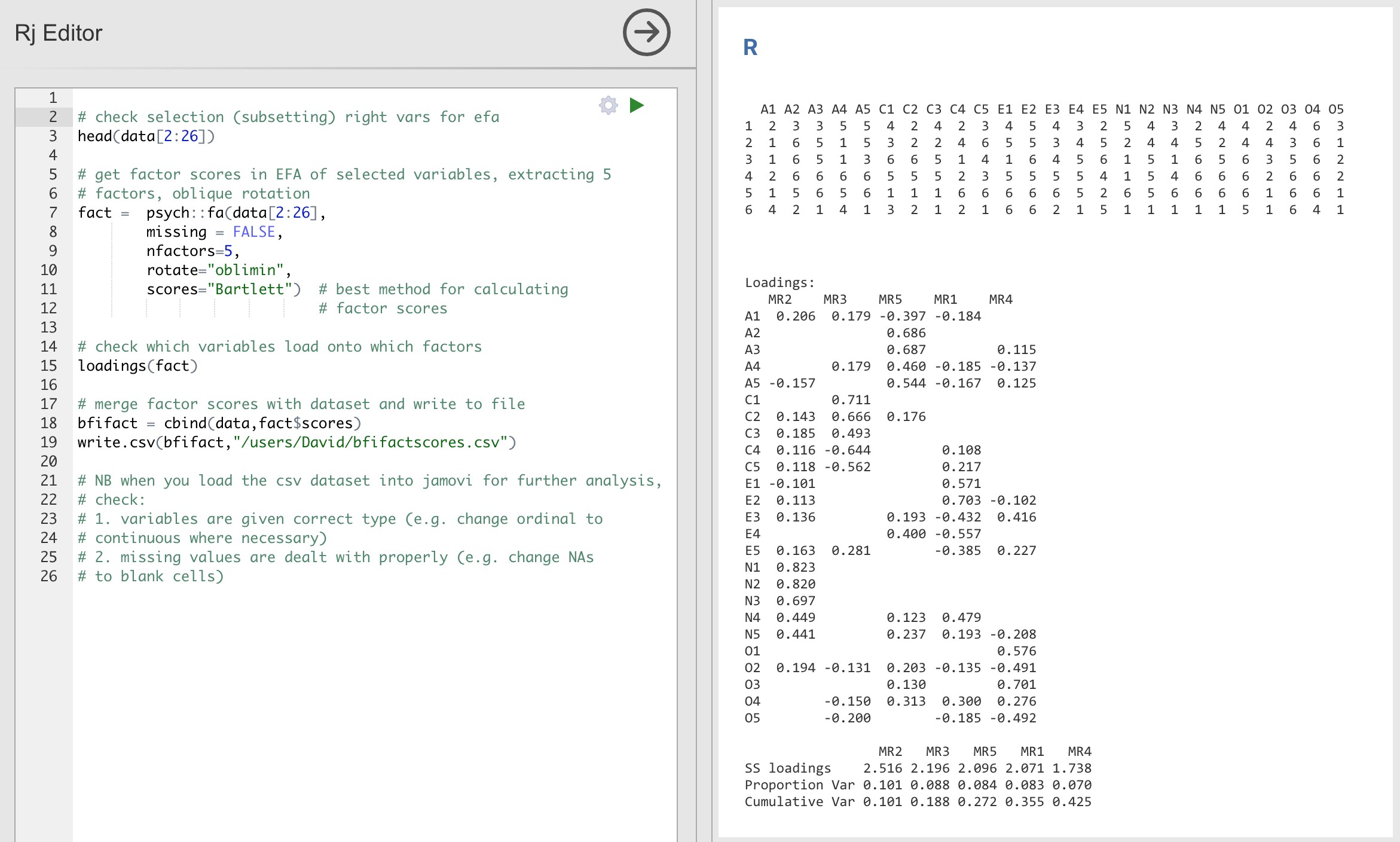
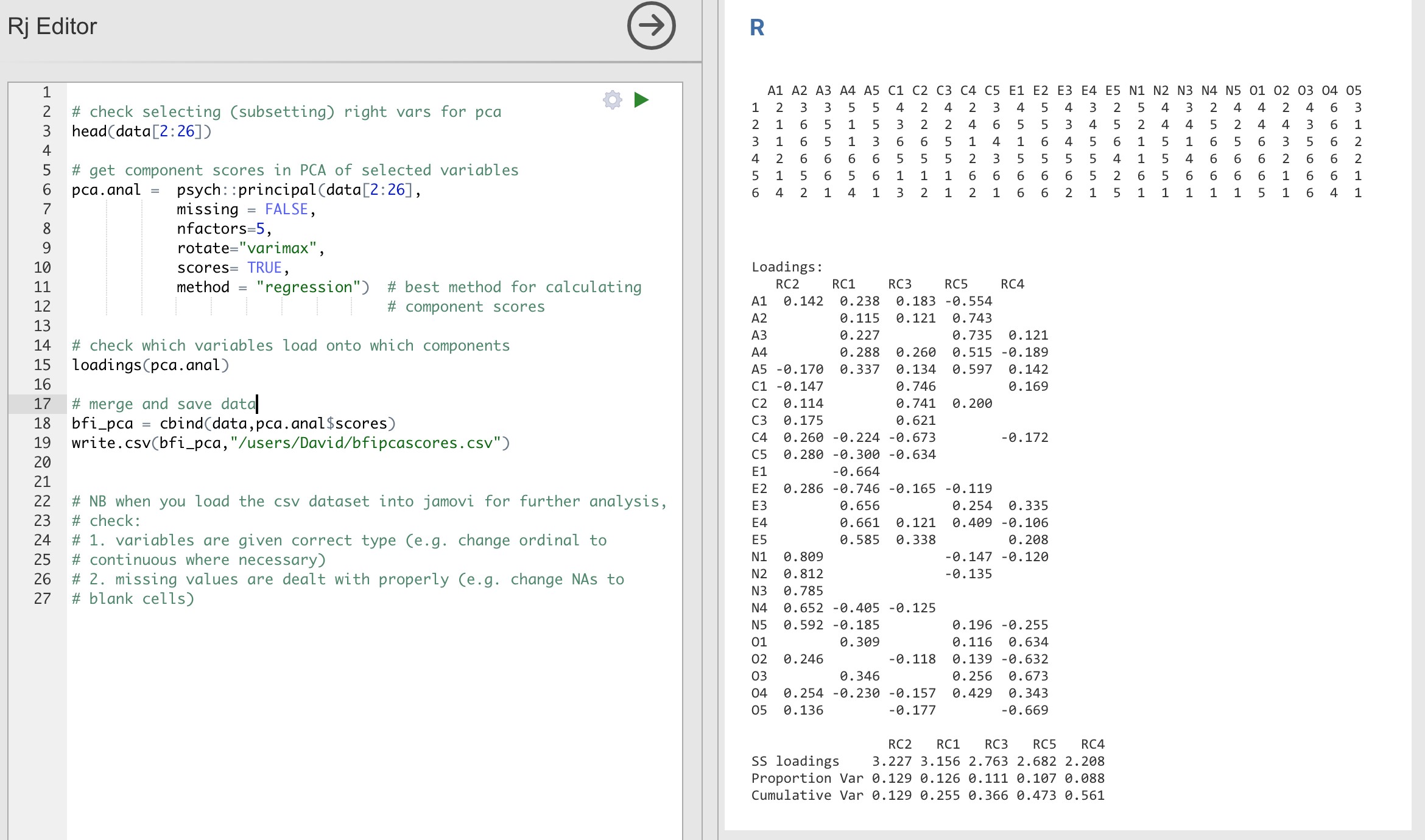
Utilisez l’éditeur Rj pour exécuter l’AFE dans R selon la même spécification que celle de Jamovi (c’est-à-dire cinq facteurs et rotation oblimin) et calculer les scores factoriels pondérés de façon optimale. Sauvegardez le nouvel ensemble de données, avec les scores factoriels, dans un fichier. Voir la Figure 15‑10 et Figure 15‑11.
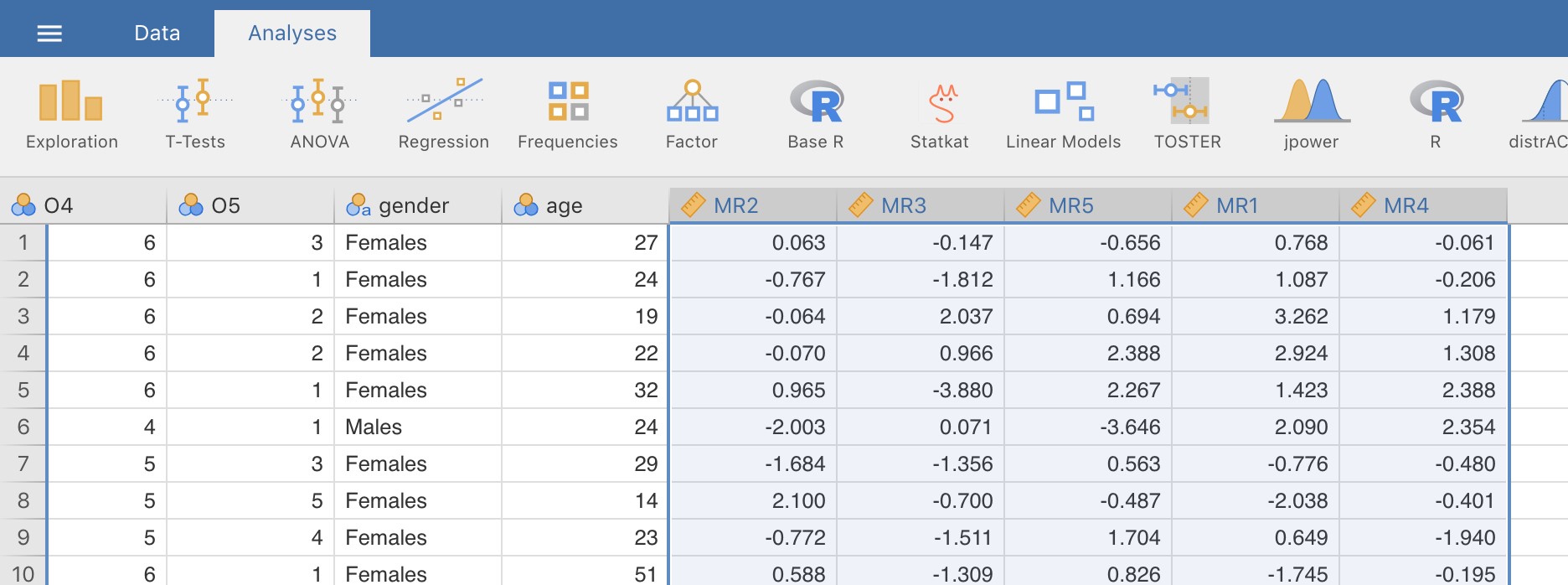
Ouvrez le nouveau fichier dans Jamovi et vérifiez que les types de variables ont été correctement définis. Étiqueter les nouvelles variables de score factoriel correspondant aux noms ou définitions des facteurs pertinents (NB : il est possible que les facteurs ne soient pas dans l’ordre prévu, vous devez donc le vérifier).
Figure 15‑10 : Commandes de l’éditeur Rj pour créer des scores factoriels pondérés de façon optimale pour la solution à cinq facteurs
Figure 15‑11 : Le nouveau fichier de données « bfifactscores.csv » créé dans l’éditeur Rj et contenant les cinq variables de score factoriel. Notez que chacune des nouvelles variables de score factoriel est étiquetée selon l’ordre dans lequel les facteurs sont énumérés dans le tableau des saturations factorielles.
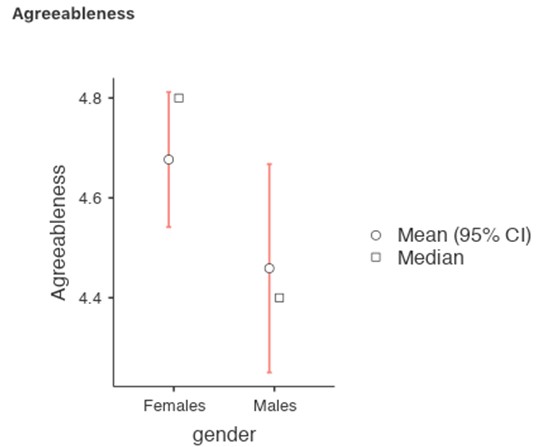
Vous pouvez maintenant procéder à d’autres analyses, soit à l’aide des scores factoriels (une approche basée sur une échelle de score moyen), soit à l’aide des scores factoriels pondérés de manière optimale calculés par l’éditeur Rj. A vous de choisir ! Par exemple, vous pourriez vous interesser aux différences entre les sexes dans chacune de nos échelles de personnalité. Nous l’avons fait pour le score d’agrément que nous avons calculé à l’aide de l’approche factorielle, et bien que le graphique (Figure 15‑12) montre que les hommes sont moins agréables que les femmes, cette différence n’est pas significative (Man-Whitney U=5760,5, p = .073).
Figure 15‑12 : Comparaison des différences entre les scores des hommes et des femmes en fonction du facteur d’agréabilité
J’espère cependant que cela vous a donné une bonne première idée de la manière d’entreprendre l’AEF dans Jamovi. Nous reviendrons sur le fouillis et la nature interprétative (une fois que vous aurez fait le travail technique) de l’analyse factorielle exploratoire dans la vraie vie un peu plus tard, juste avant de nous pencher sur l’analyse factorielle confirmatoire.
15.1.4 Le compte-rendu d’une AFE
Il n’existe pas de méthode officielle normalisée pour rédiger le compte-rendu d’une AFE, et les exemples varient selon les disciplines et les chercheurs. Cela dit, il existe des éléments d’information assez normalisés à l’égard de ce qui suit
Inclure dans votre rédaction
Les fondements théoriques pour le domaine que vous étudiez, et plus particulièrement pour les construits que vous souhaitez découvrir à travers l’AFE.
Une description de l’échantillon (p. ex. renseignements démographiques, taille de l’échantillon, méthode d’échantillonnage).
Une description du type de données utilisées (p. ex. nominales, continues) et des statistiques descriptives.
Décrivez comment vous avez procédé pour tester les hypothèses relatives à l’AFE. Les détails concernant les contrôles de sphéricité et les mesures de l’adéquation de l’échantillonnage doivent être rapportés.
Expliquer quelle méthode d’extraction de l’analyse factorielle a été utilisée (p. ex., maximum de vraisemblance).
Expliquer les critères et le processus utilisés pour décider combien de facteurs ont été extraits dans la solution finale et quels éléments ont été choisis. Expliquer clairement la raison d’être des décisions clés prises au cours du processus de l’EFA.
Expliquez quelles méthodes de rotation ont été tentées, les raisons pour lesquelles elles l’ont été et les résultats obtenus.
Les saturations factorielles finales (matrice de modèles) doivent être rapportées dans les résultats sous la forme d’un tableau. Ce tableau doit également indiquer l’unicité (ou la communauté) de chaque variable (dans la dernière colonne). Les contributions factorielles doivent être signalées au moyen d’étiquettes descriptives en plus des numéros d’items. Les corrélations entre les facteurs doivent également être incluses, soit au bas de ce tableau, dans un tableau distinct.
Les dénominations des facteurs extraits doivent être fournis. Vous souhaiterez peut-être utiliser des noms de facteurs existants, mais en examinant les items et les facteurs réels, vous penserez peut-être qu’un nom différent est plus approprié.
15.2 Analyse en composantes principales
Dans la section précédente, nous avons vu que l’AEF cherche à identifier les facteurs latents sous-jacents. Comme nous l’avons vu, dans un exemple, le plus petit nombre de facteurs latents peut être utilisé dans une analyse statistique plus poussée au moyen d’une sorte de score factoriel combiné.
De cette façon, l’AFE est utilisée comme technique de « réduction des données ». Un autre type de technique de réduction des données, parfois considérée comme faisant partie de la famille des AFE, est l’analyse en composantes principales (ACP). Cependant, l’ACP n’identifie pas les facteurs latents sous-jacents. Il crée plutôt un score composite linéaire à partir d’un ensemble plus large de variables mesurées.
L’ACP produit simplement une transformation mathématique des données d’origine sans hypothèses sur la façon dont les variables covarient. Le but de l’ACP est de calculer quelques combinaisons linéaires (composantes) des variables originales qui peuvent être utilisées pour résumer l’ensemble des données observées sans perdre beaucoup d’informations. Toutefois, si l’identification de la structure sous-jacente est un objectif de l’analyse, l’AFE est à privilégier. Comme nous l’avons vu, l’AFE produit des scores factoriels qui peuvent être utilisés à des fins de réduction des données tout comme les scores des composantes principales (Fabrigar et al. 1999).
L’ACP a été populaire en psychologie pour un certain nombre de raisons qu’il vaut la peine d’évoquer. Nous utiliserons les mêmes données bfi_sample.csv. Une grande partie de la procédure est similaire à celle de l’AFE, de sorte que, bien qu’il y ait quelques différences conceptuelles, les étapes sont pratiquement les mêmes140, et avec de grands échantillons et un nombre suffisant de variables, les résultats de l’ACP et de l’AFE devraient être assez similaires.
15.2.1 Réalisation d’une ACP avec Jamovi
Une fois que vous avez chargé les données bfi_sample.csv, sélectionnez « Factor - Principal Component Analysis » dans la barre de boutons principale de Jamovi pour ouvrir la fenêtre PCA analysis (Figure 15.13). Sélectionnez ensuite les 25 questions de personnalité et transférez-les dans la boîte « Variables ». Cochez les options appropriées, y compris les options « Check assumptions ». Dans « Method » choisissez la méthode de rotation, puis paramétrez « Number of factor to extract » et « Additionnal Outputs ». Voir la figure 15.13 pour les options suggérées pour cette ACP, Comme précédemment, veuillez noter que la méthode de rotation et le nombre de facteurs à extraire sont généralement ajustés pendant l’analyse pour trouver le meilleur résultat, comme décrit ci-dessous.
Nous commençons comme précédemment par vérifer les hypothèses sous-jacentes. Comme, vous pouvez voir (1) le test de sphéricité de Bartlett est significatif, cette hypothèse est donc satisfaite ; (2) la mesure de l’adéquation de l’échantillonnage (MSA) du KMO est globalement de 0,81, ce qui suggère une très bonne adéquation d’échantillonnage. Nous pouvons continuer.
La prochaine chose à vérifier est le nombre de composants à utiliser (ou « extraire » des données). Comme pour l’AFE, trois approches différentes sont possibles :
Une convention consiste à choisir toutes les composantes ayant des valeurs propres supérieures à 1, ce qui nous donne deux composantes avec nos données.
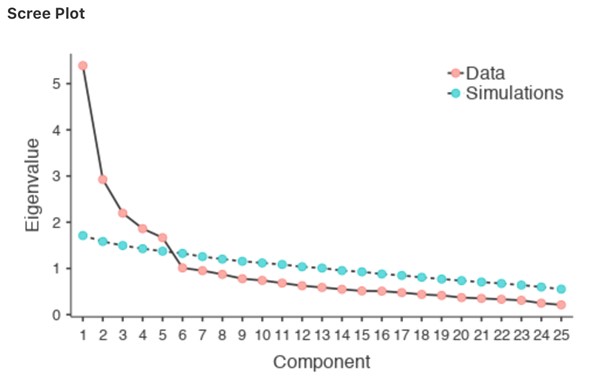
L’examen de l’éboulis, comme sur la Figure 15‑15, permet d’identifier le « point d’inflexion ». C’est le point où la pente de la courbe de l’éboulis se stabilise nettement en dessous du « coude ». Encore une fois, cela nous donnerait deux composantes puisque la stabilisation se produit clairement après la deuxième composante.
En utilisant une technique d’analyse parallèle, les valeurs propres obtenues sont comparées à celles qui seraient obtenues à partir de données aléatoires. Le nombre de composants extraits est le nombre avec des valeurs propres supérieures à ce que l’on trouverait avec des données aléatoires.
- Figure 15‑13 : Fenêtre d’analyse en composantes pincipales dans Jamovi
Comme nous l’avons dit en présentant l’AFE, la troisième approche est une bonne approche selon Fabrigar et ses collaborateurs (1999), bien qu’en pratique, les chercheurs aient tendance à examiner les trois et à porter un jugement sur le nombre de composantes qui sont les plus faciles ou les plus utiles à interpréter. Cela peut être compris comme le « critère de pertinence ». Les chercheurs examineront généralement, en plus de la solution de l’une des approches ci-dessus, des solutions comportant une ou deux composantes plus ou moins importantes. Ils adoptent ensuite la solution qui leur semble la plus logique.
Dans le même temps, nous devrions également réfléchir à la meilleure façon d’assurer la rotation de la solution finale. Là encore, comme pour l’AFE, il existe deux approches principales de la rotation : la rotation orthogonale (par exemple « varimax ») force les composantes sélectionnées à ne pas être corrélées, tandis que la rotation oblique (par exemple « oblimin ») permet la corrélation des composantes sélectionnées. Les dimensions qui intéressent les psychologues et les spécialistes du comportement ne sont pas souvent des dimensions que l’on supposerait orthogonales, de sorte que les solutions obliques sont sans doute plus raisonnables. Pratiquement, si dans une rotation oblique, les composantes sont substantiellement corrélées (c.-à-d. > 0.3) alors cela confirmerait notre intuition de préférer une rotation oblique. Si les composantes sont, en fait, corrélées, alors une rotation oblique produira une meilleure estimation des véritables composantes et une meilleure structure simple qu’une rotation orthogonale. Et, si la rotation oblique indique que les composants sont proches de corrélations nulles, alors le chercheur peut procéder à une rotation orthogonale (qui devrait alors donner à peu près la même solution que la rotation oblique).
Figure 15‑14 : Vérification des hypothèses de l’ACP dans Jamovi pour les données d’élément de personnalité
Figure 15‑15 : Courbe de l’eboulis de l’ACP dans Jamovi sur les données d’élément de personnalité montrant le point d’inflexion, le « coude », après le composant 5
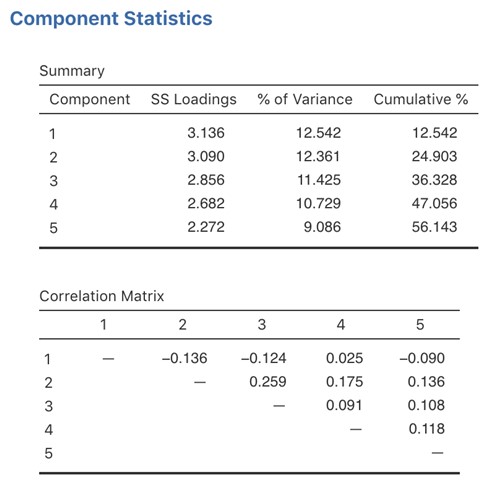
Dans la Figure 15‑16, nous voyons qu’aucune des corrélations n’est > 0,3, il est donc approprié de passer à la rotation orthogonale (varimax).
Dans la Figure 15‑16, nous avons également la proportion de la variance globale des données qui est attribuable aux deux composantes. Les composantes une et deux représentent un peu plus de 12 % de la variance chacune. Ensemble, les cinq composantes de la solution représentent un peu plus de la moitié de la variance (56 %) des données observées. Sachez que dans chaque ACP, vous pourriez potentiellement avoir le même nombre de composantes que les variables observées, mais chaque composante supplémentaire que vous incluez ajoutera une plus petite quantité de variance expliquée. Si les premières composantes expliquent une bonne partie de la variance des 25 variables initiales, alors ces composantes sont clairement un substitut utile et plus simple pour les 25 variables. Vous pouvez laisser tomber le reste sans perdre trop de la variabilité d’origine. Mais s’il faut 18 composantes pour expliquer la plus grande partie de la variance de ces 25 variables, autant utiliser les 25 variables originales.
La Figure 15‑17 montre les correlations des composants. C’est-à-dire, comment les 25 éléments de personnalité sont corrélés à chacun des composants sélectionnés. Nous avons des corrélations inférieures à 0,4 masquées (définies dans les options illustrées à la Figure 15‑13), car nous nous intéressions aux éléments ayant une corrélation importante et le fait de fixer le seuil à la valeur supérieure 0,4 nous a également fourni une solution plus propre et plus claire.
Pour les composants 1, 2, 3 et 4, la répartition des saturations des composants correspond étroitement aux facteurs présumés indiqués à la Figure 15‑2.
Figure 15‑16 : Statistiques sommaires des composants et corrélations pour une solution à cinq composants dans l’ACP dans Jamovi
Le composant 5 est assez proche, avec quatre des cinq variables observées dont on suppose qu’elles mesurent « l’ouverture » sontv assez bien corrélés avec le composant. La variable 04 ne semble pas tout à fait convenir, car la solution des composants de la Figure 15‑17 suggère qu’elle est liée au composant 4 (bien qu’avec une corrélation relativement faible) mais pas de manière substantielle sur le composant 5.
On peut également voir dans la Figure 15‑17 l’unicité de chaque variable. L’unicité est la proportion de variance qui est « spécifique » à la variable et qui n’est pas expliquée par les composantes. Par exemple, 58 % de la variance de « A1 » ne s’explique pas par les composantes de la solution à cinq composantes. En revanche, la variance de « N1 » est relativement faible et n’est pas prise en compte par la solution du composant (30%). Il est à noter que plus l’unicité est grande, plus la pertinence ou la corrélation de la variable dans le modèle des composantes est faible.
J’espère que cela vous a donné une première idée claire de la façon d’entreprendre une ACP dans Jamovi, et qu’elle est conceptuellement différente mais pratiquement similaire (si l’on dispose des bonnes données) à l’AFE.
Figure 15‑17 : Charges de composants pour une solution à cinq composants dans l’ACP de Jamovi
Vous pouvez ensuite créer les scores des composantes de la même manière que pour l’AFE. Cependant, si vous choisissez de créer un score de composant pondéré de manière optimale, les commandes et la syntaxe dans l’éditeur jamovi Rj sont un peu différentes. Voir la Figure 15‑18.
Figure 15‑18 : Commandes de l’éditeur Rj pour créer des scores de composants pondérés de manière optimale pour la solution à cinq composants
15.3 Analyse factorielle confirmatoire
Notre tentative d’identifier les facteurs latents sous-jacents à l’aide de l’AEF à l’aide de questions soigneusement sélectionnées dans le questionnaire de personnalité nous semble assez réussie. La prochaine étape dans notre quête d’une mesure utile de la personnalité est de vérifier les facteurs latents que nous avons identifiés dans l’AEF originale avec un échantillon différent. Nous voulons voir si les facteurs tiennent le coup, si nous pouvons confirmer leur existence avec des données différentes. Il s’agit d’un contrôle plus rigoureux, comme nous le verrons plus loin. C’est ce qu’on appelle l’analyse factorielle confirmatoire (AFC), car nous chercherons, sans le vouloir, à confirmer une structure factorielle latente préétablie.141
Dans l’AFC, au lieu de faire une analyse où l’on voit comment les données s’associent d’un point de vue exploratoire, nous imposons plutôt une structure aux données, comme dans la Figure 15‑19, et nous voyons dans quelle mesure les données correspondent à notre structure prédéfinie. En ce sens, nous entreprenons une analyse confirmatoire, pour voir dans quelle mesure un modèle préétabli est confirmé par les données observées.
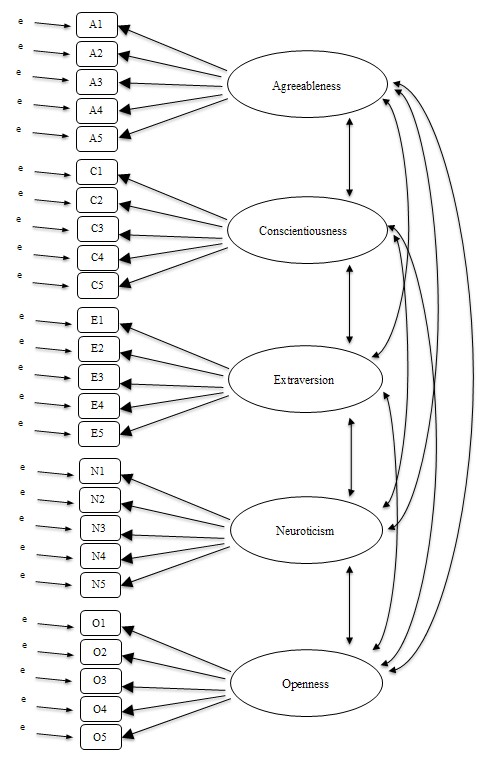
Une simple analyse factorielle de confirmation (AFC) des éléments de personnalité permettrait donc de préciser cinq facteurs latents, comme le montre la Figure 15‑19, chacun mesuré par cinq variables observées. Chaque variable est une mesure d’un facteur latent sous-jacent. Par exemple, A1 est prédit par le facteur latent sous-jacent « Agreeableness ». Dans la mesure où A1 n’est pas une mesure parfaite du facteur « Agreeableness », il y a un terme d’erreur, e, qui lui est associé. En d’autres termes, e représente la variance dans A1 qui n’est pas prise en compte par le facteur d’agréabilité. C’est ce qu’on appelle parfois l’erreur de mesure.
L’étape suivante consiste à déterminer si les facteurs latents peuvent être corrélés à notre modèle. Comme nous l’avons mentionné précédemment, dans les sciences psychologiques et comportementales, les constructions sont souvent liées les unes aux autres, et nous pensons aussi que certains de nos facteurs de personnalité peuvent être corrélés les uns aux autres. Ainsi, dans notre modèle, nous devrions permettre à ces facteurs latents de varier conjointement, comme le montrent les flèches doubles de la Figure 15‑19.
En même temps, nous devrions nous demander s’il existe une raison valable et systématique pour que certains termes d’erreur soient corrélés les uns aux autres. L’une des raisons pourrait être qu’il existe une caractéristique méthodologique commune pour des sous-ensembles particuliers des variables observées, de sorte que les variables observées pourraient être corrélées pour des raisons méthodologiques plutôt que de facteurs latents importants. Nous reviendrons sur cette possibilité dans une section ultérieure, mais, pour l’instant, il n’y a aucune raison claire qui justifierait la corrélation de certains termes d’erreur entre eux.
En l’absence de termes d’erreur corrélés, le modèle que nous testons pour voir dans quelle mesure il correspond à nos données d’observation est conforme à ce qui est indiqué à la Figure 15‑19. Seuls les paramètres inclus dans le modèle sont censés se trouver dans les données, de sorte que dans l’ACC, tous les autres paramètres possibles sont mis à zéro. Ainsi, si ces autres paramètres ne sont pas nuls (par exemple, il peut y avoir une charge substantielle de A1 sur le facteur latent Extraversion dans les données observées, mais pas dans notre modèle) alors nous pouvons trouver une mauvaise correspondance entre notre modèle et les données observées.
Figure 15‑19 : Pré-spécification initiale de la structure des facteurs latents pour les échelles de personnalité à cinq facteurs, à utiliser en CFA
Voyons comment nous avons réalisée cette analyse CFA avec Jamovi.
15.3.1 L’AFC avec Jamovi
Ouvrez le fichier bfi_sample2.csv, vérifiez que les 25 variables sont codées comme ordinales (ou continues ; cela ne fera aucune différence pour cette analyse) dans Jamovi pour faire l’AFC :
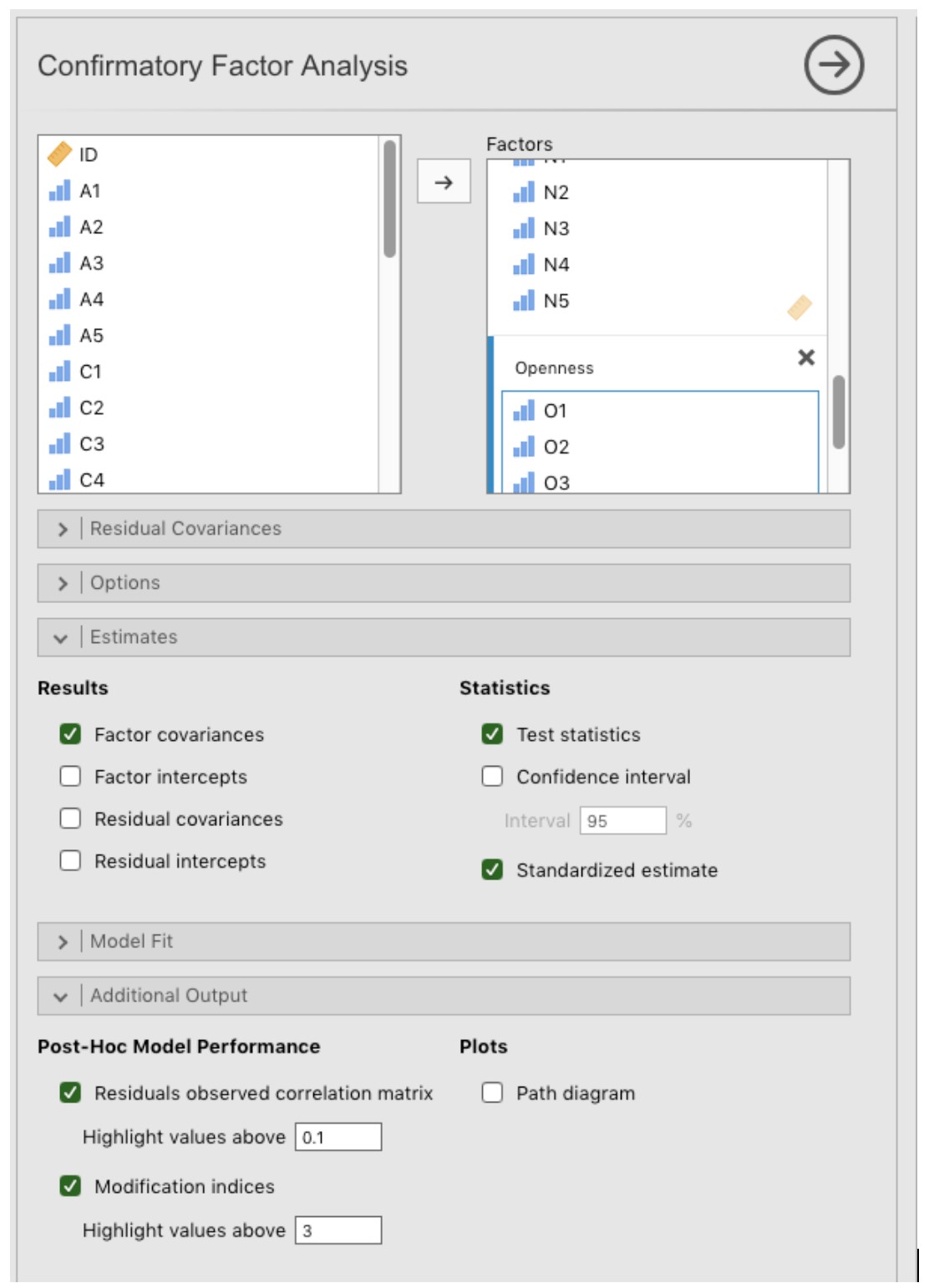
Sélectionnez « Factor - Confirmatory Factor Analysis » dans la barre de boutons Jamovi principale pour ouvrir la fenêtre CFA analysis (Figure 15‑20).
Sélectionnez les 5 variables A et transférez-les dans la case ‘Factors’ et donnez ensuite le label « Agreeableness ».
Créez un nouveau Facteur dans la case « Facteurs » et nommez-le « Conscientiousness ». Sélectionnez les 5 variables C et transférez-les dans la case « Factors » sous le titre « Conscientiousness ».
Créez un autre nouveau facteur dans la case ‘Factors’ et nommez-le « Extraversion ». Sélectionnez les 5 variables E et les transférer dans la case « Factors » sous le titre « Extraversion ».
Créez un autre nouveau facteur dans la boîte « Factors » et nommez-le « Neuroticism ». Sélectionnez les 5 variables N et les transférer dans la case « Factors » sous le titre « Neuroticism ».
Créez un autre nouveau Facteur dans la case « Factors » et nommez-le « Openness ». Sélectionnez les 5 variables O et les transférer dans la case « Factors » sous le titre « Openness ».
Cochez les autres options pertinentes, les valeurs par défaut sont correctes pour ce premier travail, vous pouvez également cocher l’option « Path diagram » sous « Plots » pour demander à Jamovi produire un diagramme (assez) similaire à notre Figure 15‑19.
Figure 15‑20 : La fenêtre d’analyse pour analyse factorielle confirmatoire (AFC) dans Jamovi
Une fois que nous avons mis en place l’analyse, nous pouvons examiner la fenêtre des résultats de Jamovi et voir ce qu’il en est. La première chose à examiner est l’ajustement du modèle (Figure 15‑21), car cela nous indique si notre modèle correspond bien aux données observées. Dans notre modèle, seules les covariances prédéfinies sont estimées, y compris les corrélations de facteurs par défaut. Tout le reste est mis à zéro.
Il existe plusieurs façons d’évaluer l’adéquation du modèle. La première est une statistique du chi carré qui, si elle est petite, indique que le modèle est bien adapté aux données. Cependant, la statistique du chi carré utilisée pour évaluer l’ajustement du modèle est assez sensible à la taille de l’échantillon, ce qui signifie qu’avec un grand échantillon, un ajustement suffisamment bon entre le modèle et les données produit presque toujours une valeur du chi carré importante et significative (p.<.05).
Nous avons donc besoin d’autres moyens d’évaluer l’adéquation du modèle. Dans Jamovi plusieurs sont fournis par défaut. Il s’agit de l’indice d’ajustement comparatif (CFI), de l’indice de Tucker Lewis (TLI) et de l’erreur quadratique moyenne quadratique approximative (RMSEA) ainsi que de l’intervalle de confiance à 90 % pour la RMSEA. Quelques règles empiriques utiles nous indiquent qu’un ajustement satisfaisant est indiqué par CFI > 0.9, TLI > 0.9, et RMSEA entre 0,05 et 0,08. Un bon ajustement est CFI > 0.95, TLI > 0.95, et RMSEA et CI supérieur pour RMSEA < 0.05.
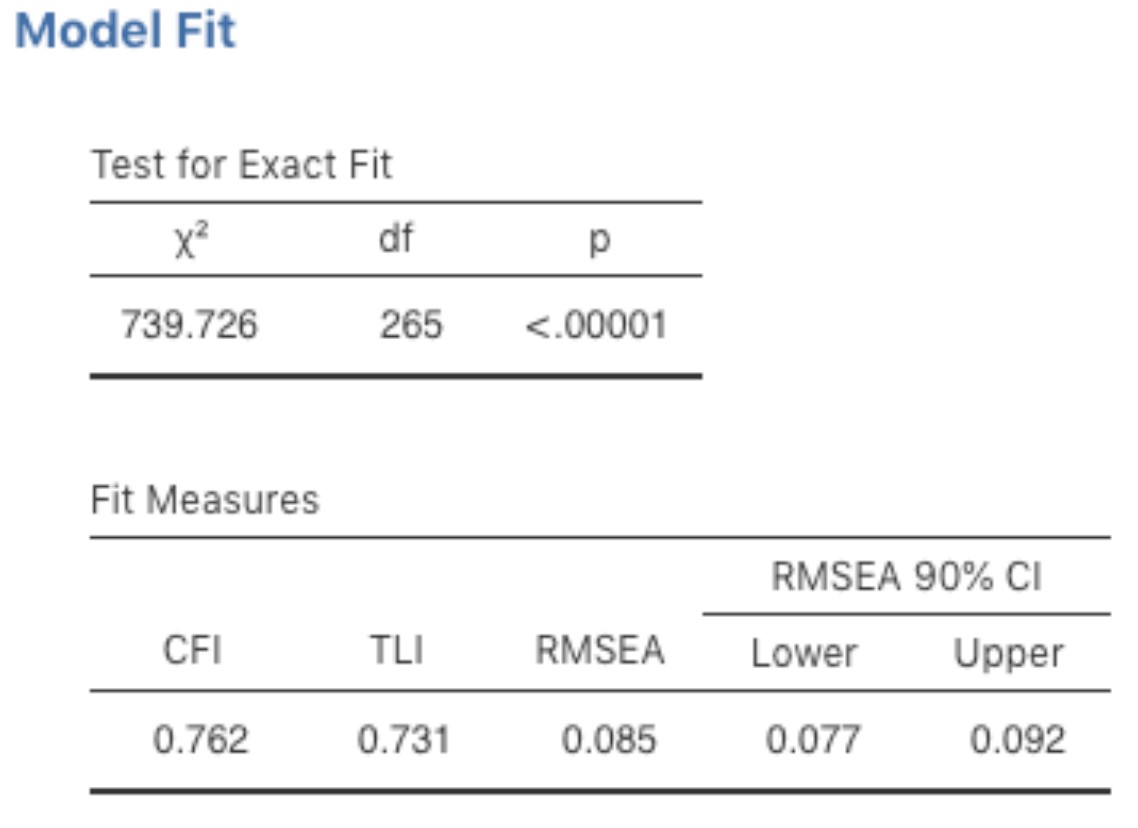
Figure 15‑21 : Résultats de l’ajustement du modèle AFC Jamovi pour notre modèle CFA
Ainsi, en regardant la Figure 15‑21, nous pouvons voir que la valeur du chi carré est grande et très significative. La taille de notre échantillon n’est pas trop grande, ce qui indique peut-être un mauvais ajustement. La CFI est de 0,762 et la TLI est de 0,731, ce qui indique un mauvais ajustement entre le modèle et les données. La RMSEA est de 0,085 avec un intervalle de confiance à 90 % de 0,077 à 0,092, ce qui, encore une fois, n’indique pas un bon ajustement.
Plutôt décevant, hein ? Mais ce n’est peut-être pas trop surprenant étant donné que, dans l’ancien AFE, nous utilisions un ensemble de données semblable (section 15.1), le modèle à cinq facteurs ne représentait que la moitié environ de la variance des données.
Figure 15‑22 : Le tableau des saturation factorielles dans l’AFC réalisée avec Jamovi pour notre modèle
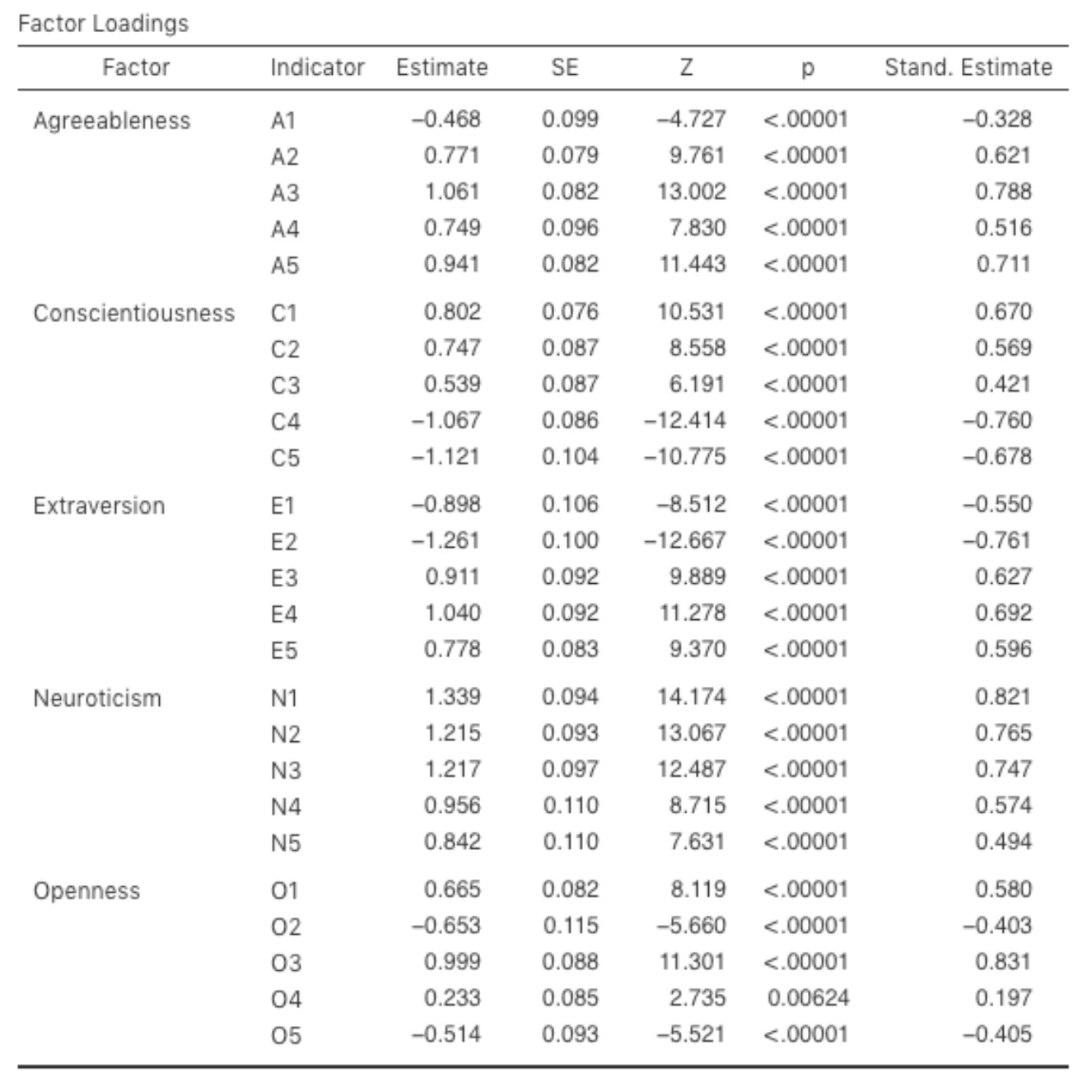
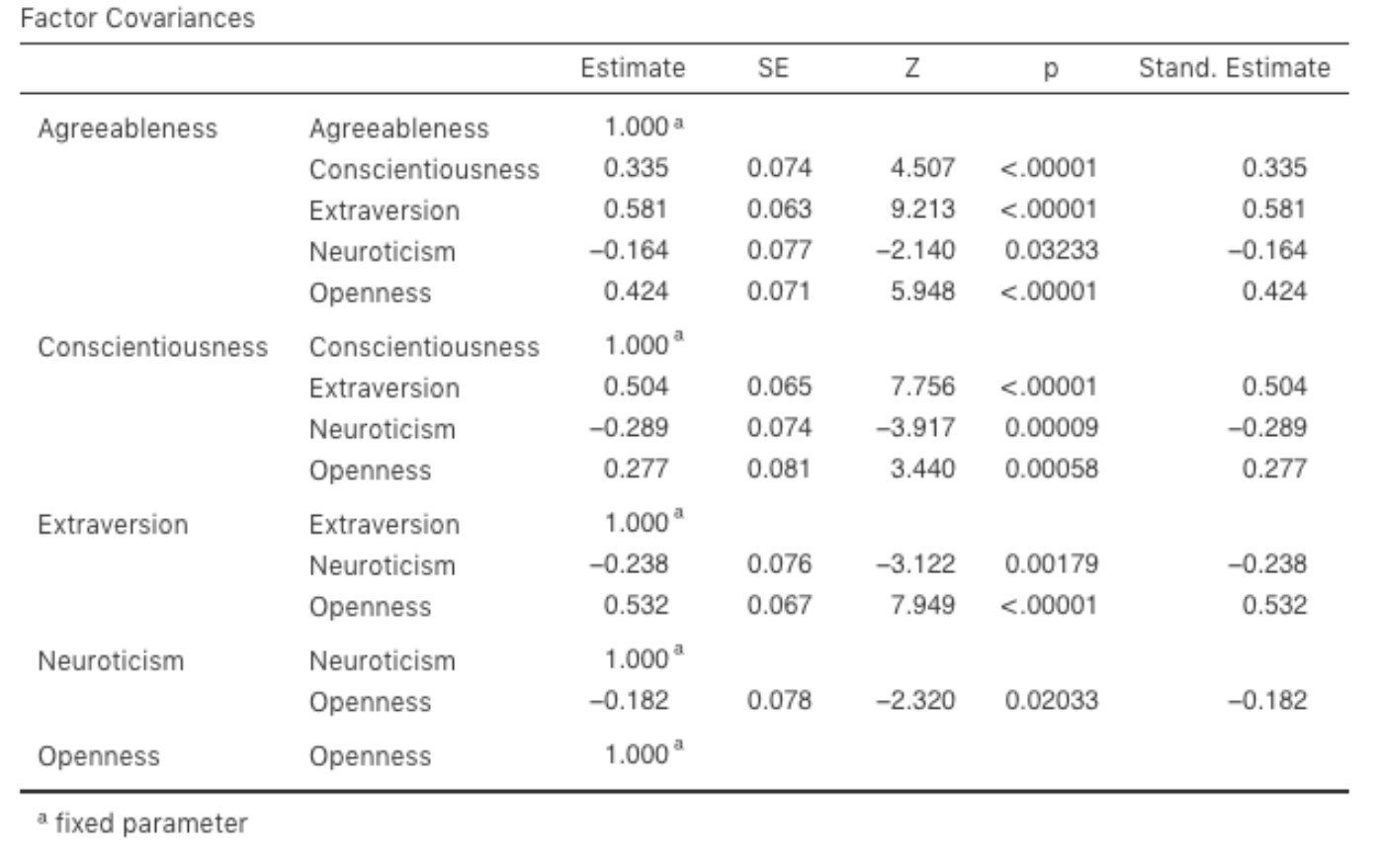
Examinons ensuite les saturations factorielles et les estimations de covariance des facteurs, illustrées aux Figure 15‑22 et Figure 15‑23. La statistique Z et la valeur p de chacun de ces paramètres indiquent qu’ils apportent une contribution raisonnable au modèle (c.-à-d. qu’ils ne sont pas nuls), de sorte qu’il ne semble y avoir aucune raison de supprimer du modèle les relations facteurs-variables ou les corrélations facteur-facteur spécifiés. Souvent, les estimations normalisées sont plus faciles à interpréter, et elles peuvent être précisées dans l’option « Estimates ». Ces tableaux peuvent utilement être incorporés dans un rapport écrit ou un article scientifique.
Figure 15‑23 : Le tableau des covariances des facteurs de notre modèle d’AFC calculées avec Jamovi
Comment pourrions-nous améliorer le modèle ? L’une des options consiste à revenir en arrière et à réfléchir aux éléments ou mesures que nous utilisons et à la façon dont ils pourraient être améliorés ou modifiés. Une autre option est de faire quelques ajustements post-hoc sur le modèle pour améliorer l’ajustement. Une façon d’y parvenir est d’utiliser des « indices de modification », demandés dans option « Additionnal Output » dans Jamovi (voir Figure 15‑24).
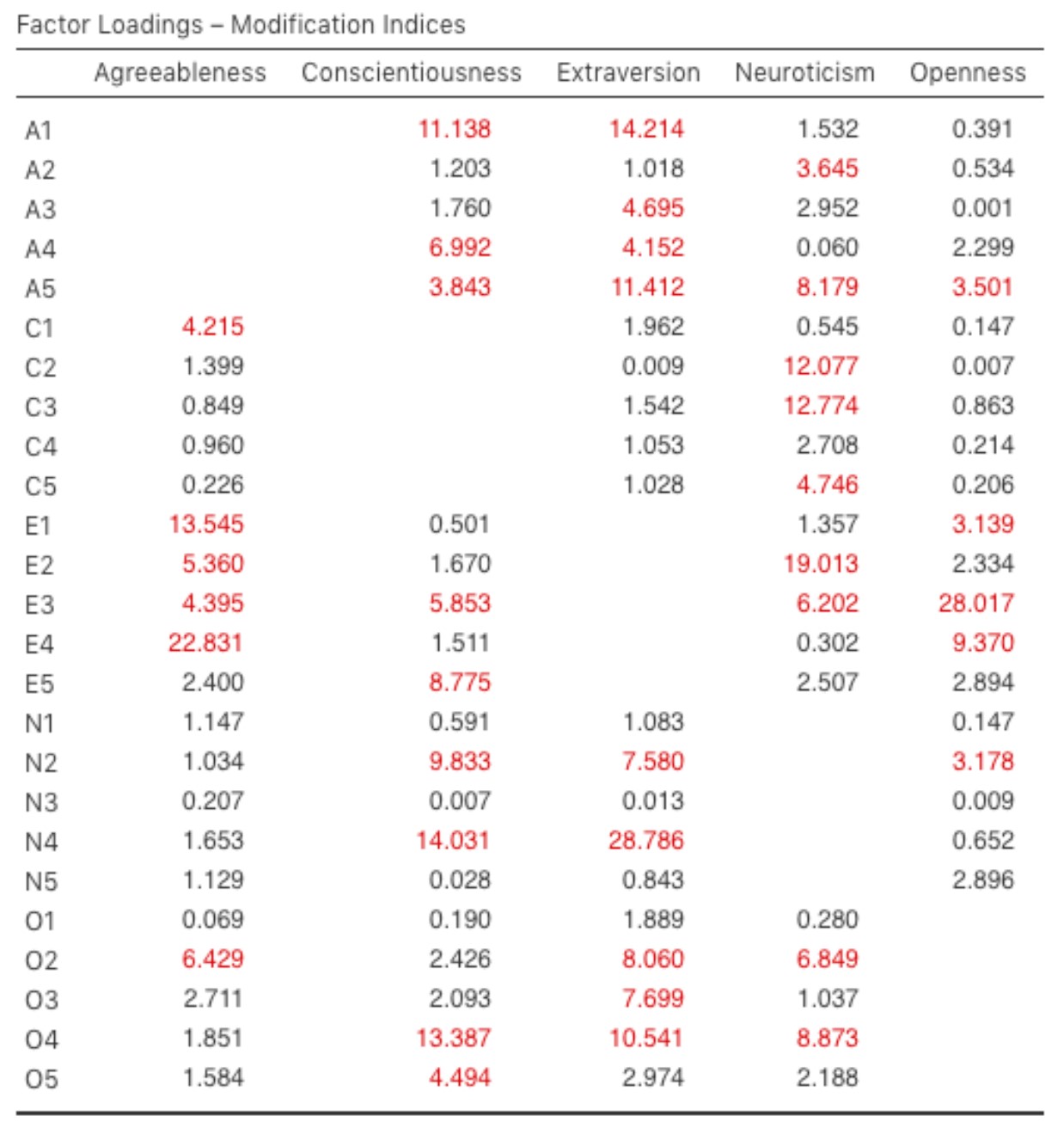
Ce que nous recherchons, c’est la valeur la plus élevée de l’indice de modification (MI). Nous jugerons alors s’il est judicieux d’ajouter ce terme supplémentaire dans le modèle, en utilisant une analyse post-hoc. Par exemple, nous pouvons voir à la Figure 15‑24 que le MI le plus élevé pour les facteurs qui ne sont pas déjà dans le modèle est une valeur de 28,786 pour la contribution de N4 (« Often feel blue ») sur le facteur latent « Extraversion ». Cela indique que si nous ajoutons cette relation dans le modèle, la valeur du chi carré diminuera d’environ le même montant.
Figure 15‑24 : Indices de modification des saturations des facteurs de l’AFC dans Jamovi
Mais dans notre modèle, l’ajout de cette relation n’a sans doute aucun sens théorique ou méthodologique, et n’est donc pas une bonne idée (à moins que vous ne puissiez trouver un argument persuasif selon lequel le fait d’être « Sentir souvent triste » mesure à la fois le névrotisme et l’extraversion). Moi, je ne peux pas. Mais, pour les besoins de l’argumentation, supposons que cela ait un sens et ajoutons ce lien dans le modèle. Retournez à la fenêtre d’analyse CFA (voir Figure 15‑20) et ajoutez N4 dans le facteur d’Extraversion. Les résultats du AFC vont maintenant changer (non montrés) ; le khi-carré est descendu à environ 709 (une baisse d’environ 30, à peu près similaire à la taille du MI) et les autres indices d’ajustement se sont également améliorés, mais seulement un peu. Mais ce n’est pas assez ; ce n’est toujours pas un bon modèle.
Si vous ajoutez de nouveaux paramètres à un modèle à l’aide des valeurs MI, vérifiez toujours à nouveau les tables MI après chaque nouvel ajout, car les MI sont actualisés à chaque fois.
Figure 15‑25 : Indices de modification des covariances résiduelles dans l’AFC avec Jamovi
Il existe également un tableau des Indices de Modifications de Covariance Résiduelle produit par jamovi (Figure 15‑25). En deux mots, c’est un tableau indiquant les erreurs corrélées, qui si elles étaient ajoutées au modèle, amélioreraient le plus l’ajustement du modèle. C’est une bonne idée de vérifier les deux tables de MI en même temps, de repérer le MI le plus grand, de se demander si l’ajout du paramètre suggéré peut être raisonnablement justifié et, si possible, de l’ajouter au modèle. Ensuite, vous pouvez recommencer à chercher le plus grand MI dans les résultats recalculés.
Vous pouvez continuer de cette façon aussi longtemps que vous le souhaitez, en ajoutant des paramètres au modèle basé sur le MI le plus grand, et finalement vous obtiendrez un ajustement satisfaisant. Mais il y aura aussi une forte probabilité qu’en faisant cela vous ayez créé un monstre ! Un modèle laid et déformé qui n’a aucun sens théorique, ni aucune pureté. En d’autres termes, soyez très prudent !
Jusqu’à présent, nous avons vérifié la structure factorielle obtenue dans l’AFE à l’aide d’un deuxième échantillon et de l’AFC. Malheureusement, nous n’avons pas trouvé que la structure factorielle de l’AEF avait été confirmée dans l’AFC, ce qui nous ramène à la case départ pour ce qui est de l’élaboration de cette échelle de personnalité.
Même si nous avions pu modifier l’AFC à l’aide d’indices de modification, il n’y avait pas de bonnes raisons (qui me viennent à l’esprit) d’inclure d’autres saturations factorielles ou covariances résiduelles. Cependant, il y a parfois une bonne raison de permettre aux résidus de covarier (ou de corréler), et un bon exemple en est donné dans la section suivante sur l’AFC multitraits multiméthodes (Multi-Trait Multi-Method (MTMM) CFA). Avant de faire cela, expliquons comment communiquer les résultats d’une AFC.
15.3.2 Compte-rendu d’une AFC
Il n’existe pas de méthode officielle normalisée pour faire un compte-rendu d’une AFC, et les exemples varient selon la discipline et le chercheur. Cela dit, il y a des éléments d’information assez standard à inclure dans votre rapport :
Une justification théorique et empirique du modèle hypothétique.
Une description complète de la façon dont le modèle a été spécifié (c.-à-d. les variables indicatrices pour chaque facteur latent, les covariances entre les variables latentes et toute corrélation entre les termes d’erreur). Il serait bon d’inclure un diagramme des relations, comme celui de la Figure 15‑21.
Une description de l’échantillon (p. ex. renseignements démographiques, taille de l’échantillon, méthode d’échantillonnage).
Une description du type de données utilisées (p. ex. nominales, continues) et des statistiques descriptives.
Tests des hypothèses et de la méthode d’estimation utilisées.
Une description des données manquantes et la façon dont elles ont été traitées.
Le logiciel et la version utilisés pour adapter le modèle.
Les mesures et les critères utilisés pour juger de l’adéquation du modèle.
Toute modification apportée au modèle original en fonction des indices d’ajustement ou de modification du modèle.
Toutes les estimations de paramètres (c.-à-d. les saturations, les variances d’erreur, les (co)variances latentes et leurs erreurs types, probablement dans un tableau).
15.4 Multi-Trait Multi-Méthode Multi-Method CFA
Dans cette section, nous allons examiner comment différentes techniques de mesure ou questions peuvent constituer une source importante de variabilité des données, appelée méthode variance. Pour ce faire, nous utiliserons un autre ensemble de données psychologiques, celui qui contient des données sur le « style attributif ».
Avec le questionnaire de style attributif, (Attributional Style Questionnaire ou ASQ), Hewitt, Foxcroft et MacDonald (2004) ont collecté des données sur le bien-être psychologique des jeunes au Royaume-Uni et en Nouvelle-Zélande. Ils ont mesuré le style attributif d’événements négatifs, c’est-à-dire la façon dont les gens expliquent habituellement la cause des mauvaises choses qui leur arrivent (Peterson and Seligman 1984). Le questionnaire sur le style attributif (ASQ) mesure trois aspects du style attributif :
L’internalité est la mesure de la croyance d’une personne que la cause d’un mauvais événement est due à ses propres actions.
La stabilité mesure la croyance d’une personne que la cause d’un mauvais événement est stable dans le temps.
La globalité renvoie à la mesure de la croyance d’une personne que la cause d’un mauvais événement dans un domaine affectera d’autres domaines de sa vie.
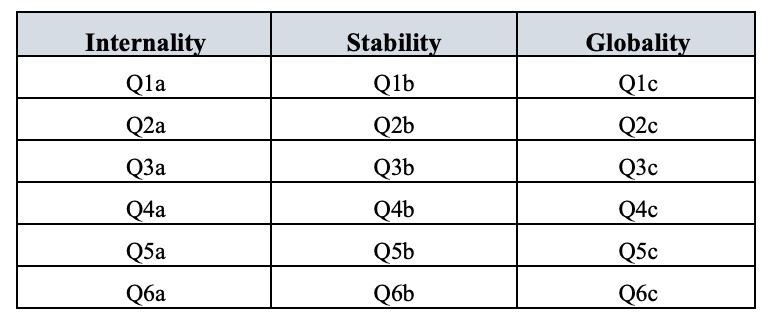
Il y a six scénarios hypothétiques et pour chaque scénario, les répondants répondent à une question visant à déterminer (a) l’internalité, (b) la stabilité et (c) la globalité. Il y a donc 6 x 3 = 18 items au total. Voir la Figure 15‑26 pour plus de détails.
Figure 15‑26 : Questionnaire sur le style attributif (QSA) pour les événements négatifs
Les chercheurs ont cherché à vérifier leurs données pour voir s’il y a des facteurs latents sous-jacents qui sont raisonnablement bien mesurés par les 18 variables observées dans le QSA.
Ils ont d’abord, essayé l’AFE avec ces 18 variables (non montrées), mais peu importe la façon dont elles sont extraites ou en rotation, ils n’ont pas trouvé de bonne solution factorielle. Leur tentative d’identifier les facteurs latents sous-jacents dans le questionnaire sur le style attributif (QSA) s’est avérée infructueuse.
Si vous obtenez de tels résultats, soit votre théorie est erronée (il n’y a pas de structure sous-jacente de facteurs latents pour le style attributif, ce qui est possible), soit l’échantillon n’est pas pertinent (ce qui est peu probable étant donné la taille et les caractéristiques de cet échantillon de jeunes adultes du Royaume-Uni et de Nouvelle-Zélande), soit l’analyse ne constitue pas le bon outil pour cet emploi. Nous allons examiner cette troisième possibilité.
Rappelons qu’il y avait trois dimensions mesurées dans l’ASQ : Internalité, Stabilité et Globalité, chacune mesurée par six questions, comme le montre la Figure 15‑27.
Figure 15‑27 : Six questions sur l’ASQ pour chacune des dimensions Internalité, Stabilité et Globalité
Que se passerait-il si, au lieu de faire une analyse où nous voyons comment les données sont regroupées de façon exploratoire, nous imposions plutôt une structure, comme celle de la Figure 15‑27, aux données et voyions dans quelle mesure les données correspondent à notre structure prédéfinie. En ce sens, nous entreprenons une analyse de confirmatoire, pour voir dans quelle mesure un modèle préétabli est confirmé par les données observées.
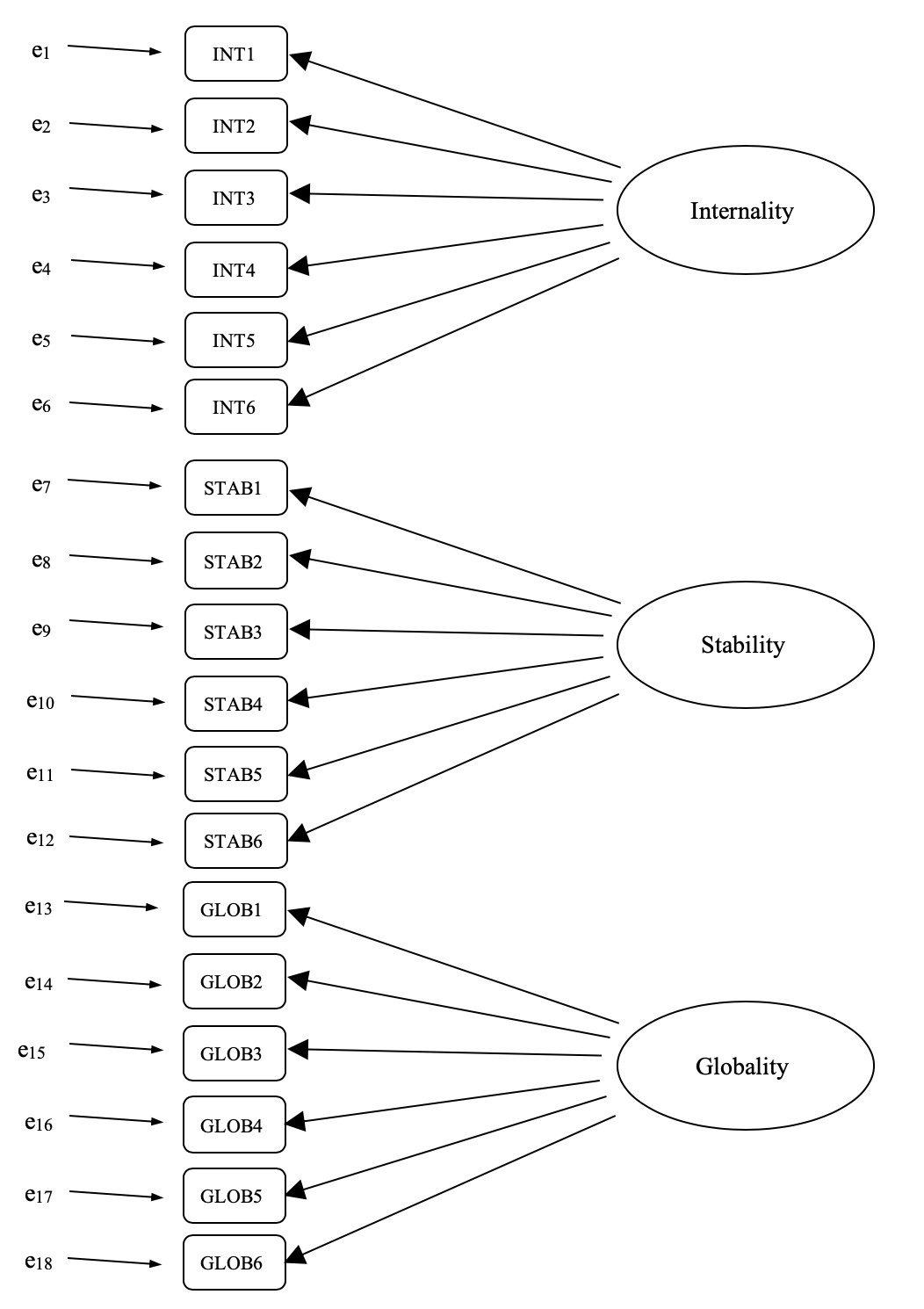
Une simple analyse factorielle confirmatoire (AFC) de l’ASQ indiquerait donc trois facteurs latents, comme le montrent les colonnes de la Figure 15‑27, chacun mesuré par six variables observées.
Nous pourrions les représenter comme dans le diagramme de la Figure 15‑28, qui montre que chaque variable est une mesure d’un facteur latent sous-jacent. Par exemple, INT1 est prédit par le facteur latent sous-jacent Internalité. Et comme INT1 n’est pas une mesure parfaite du facteur d’internalité, il y a un terme d’erreur, e1, qui lui est associé. En d’autres termes, e1 représente la variance dans INT1 qui n’est pas prise en compte par le facteur d’internalité. C’est ce qu’on appelle parfois une « erreur de mesure ».
L’étape suivante consiste à déterminer si les facteurs latents peuvent être corrélés dans notre modèle. Comme nous l’avons mentionné précédemment, dans les sciences psychologiques et comportementales, les constructions sont souvent liées les unes aux autres, et nous pensons aussi que l’internalité, la stabilité et la globalité peuvent être corrélées les unes aux autres, de sorte que dans notre modèle nous devrions permettre à ces facteurs latents de varier conjointement, comme le montre la Figure 15‑29.
Parallèlement, nous devrions nous demander s’il existe une raison valable et systématique pour que certains termes d’erreur soient corrélés les uns aux autres. En repensant aux questions de l’ASQ, on constate qu’il y a trois sous-questions différentes (a, b et c) pour chaque question principale (1-6). Q1 était relative à la recherche d’emploi infructueuse et il est plausible que cette question ait des particularités artefactuels ou méthodologiques qui la distinguent des autres questions (2-5) et qui aurait quelque chose à voir avec la difficulté à trouver du travail. De même, Q2 était relative à l’aide refusée à un ami qui avait un problème, et il se peut qu’il n’y ait pas de problèmes artéfactuels ou méthodologiques distinctifs liés au fait de ne pas aider un ami qui ne seraient pas présent dans les autres questions (1 et 3-5).
Figure 15‑28 : Pré-spécification initiale de la structure factorielle latente pour l’ASQ
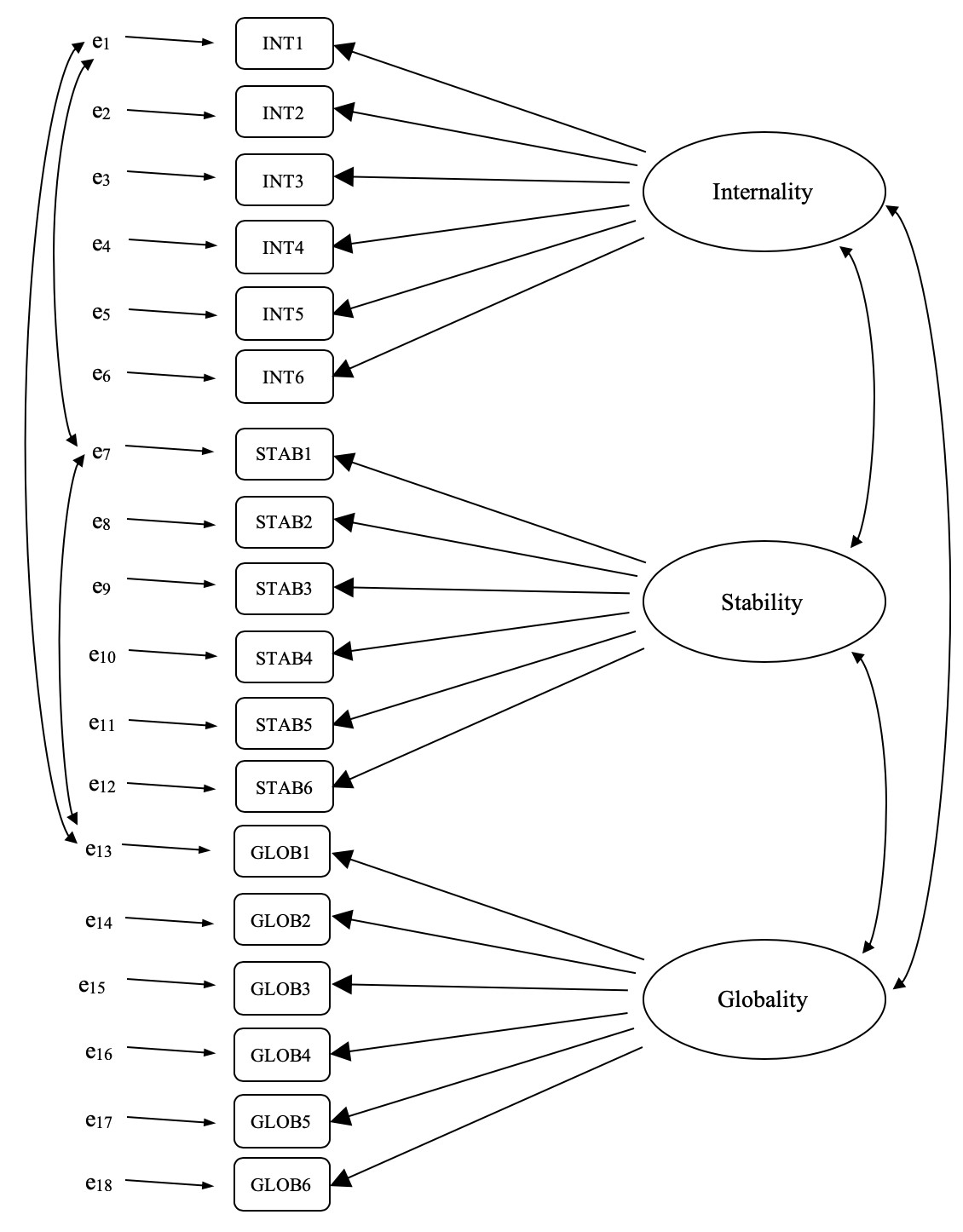
Ainsi, en plus de facteurs multiples, nous avons également de multiples caractéristiques méthodologiques dans l’ASQ, où chacune des questions 1 à 6 a une « méthode » légèrement différente, mais chaque « méthode » est partagée entre les sous-questions a, b et c. Afin d’intégrer ces différentes caractéristiques méthodologiques dans le modèle, nous pouvons spécifier que certains termes d’erreur sont corrélés les uns aux autres. Par exemple, les erreurs associées à INT1, STAB1 et GLOB1 devraient être corrélées entre elles pour refléter la variance méthodologique distincte et partagée de Q1a, Q1b et Q1c. Si l’on examine la Figure 15‑27, cela signifie qu’en plus des facteurs latents représentés par les colonnes, nous aurons corrélé les erreurs de mesure pour les variables de chaque rangée du tableau.
Figure 15‑29 : Pré-spécification finale de la structure des facteurs latents pour l’ASQ, y compris les corrélations des facteurs latents et les corrélations des termes d’erreur pour les variables observées INT1, STAB1 et GLOB1, dans un modèle d’AFC MTMM. Par souci de clarté, les autres corrélations de termes d’erreur préétablies ne sont pas indiquées.
Bien qu’un modèle d’AFC de base comme celui illustré à la Figure 15‑28 puisse être comparé à nos données observées nous avons en fait mis au point un modèle plus sophistiqué, comme le montre le diagramme de la Figure 15‑29. Ce modèle d’AFC plus sophistiqué est connu sous le nom de modèle Multi-Trait Multi-Method (MTMM), et c’est celui que nous allons tester à Jamovi.
15.4.1 Faire une AFC MTMM avec Jamovi
Ouvrez le fichier ASQ.csv et vérifiez que les 18 variables (six variables « Internalité », six variables « Stabilité » et six variables « Globalité ») sont codées comme continue.
Pour effectuer l’AFC MTMM CFA dans Jamovi :
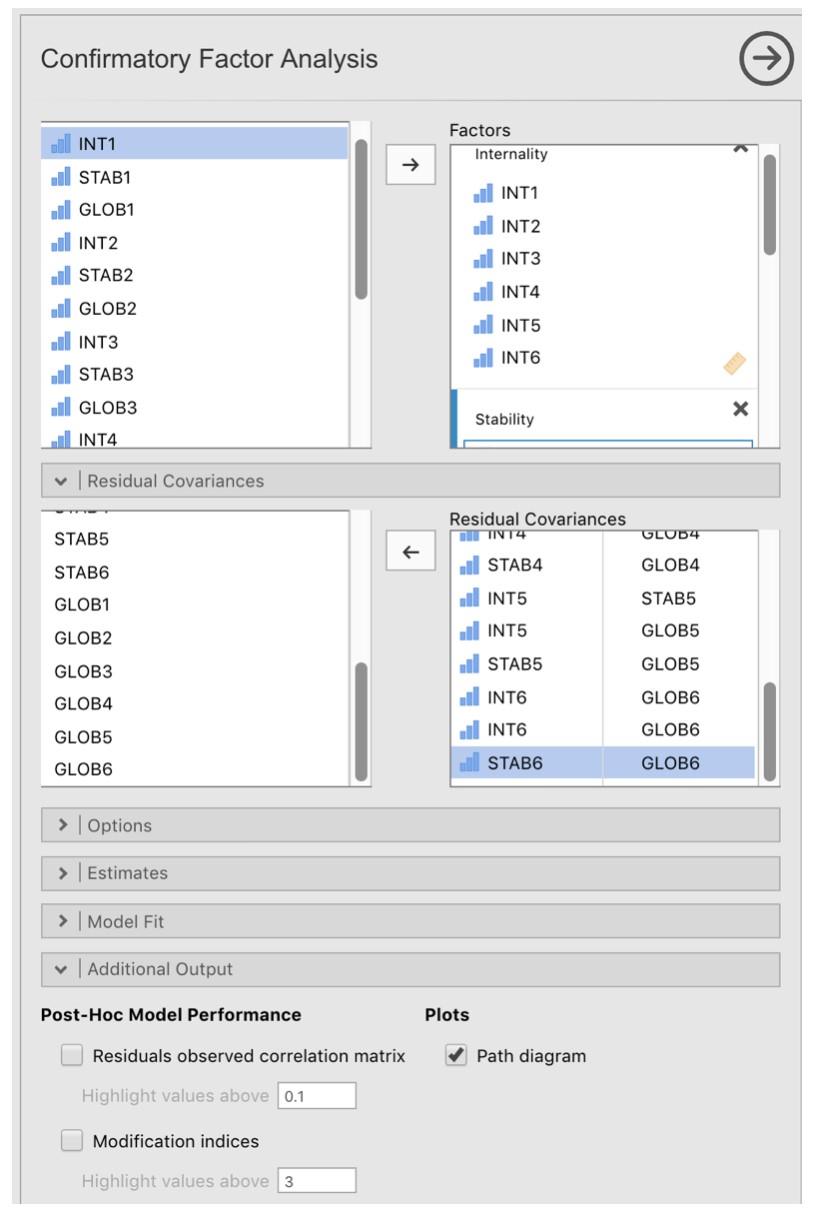
Sélectionnez Factor - Confirmatory Factor Analysis dans la barre de boutons Jamovi principale pour ouvrir la fenêtre CFA analysis (Figure 15‑30).
Sélectionnez les 6 variables INT et transférez-les dans la case « Factors » et donnez ensuite le label « Internalité ».
Créez un nouveau facteur dans la case ‘Factors’ et nommez-le « Stabilité ». Sélectionnez les 6 variables STAB et les transférer dans la case « Facteurs » sous le titre « Stabilité ».
Créez un autre nouveau Facteur dans la case « Facteurs » et nommez-le « Globalité ». Sélectionnez les 6 variables GLOB et transférez-les dans la case « Facteurs’ » sous le titre « Globalité ».
Ouvrez les options « Residual Covariances », et pour chacune de nos corrélations prédéfinies, déplacez les variables associées dans la case « Residual Covariances » à droite. Par exemple, sélectionnez INT1 et STAB1, puis cliquez sur la flèche pour les déplacer. Faites de même pour INT1 et GLOB1, pour STAB1 et GLOB1, pour INT2 et STAB2, pour INT2 et GLOB2, pour STAB2 et GLOB2, pour INT3 et STAB3, etc.
Cochez d’autres options appropriées, les valeurs par défaut sont correctes pour ce premier travail, mais vous pouvez cocher l’option « Path diagram » sous « Plots » pour que Jamovi dessine un diagramme (assez) similaire à notre Figure 15‑29, mais incluant toutes les corrélations des termes d’erreur que nous avons ajouté ci-dessus.
Une fois que nous avons réalisé l’analyse, nous pouvons porter notre attention sur la fenêtre des résultats de Jamovi et voir ce qu’il en est. La première chose à examiner est « l’ajustement du modèle », car cela nous indique dans quelle mesure notre modèle correspond bien aux données observées. Dans notre modèle, seules les covariances pré-spécifiées sont estimées, tout le reste est mis à zéro, donc l’ajustement du modèle teste à la fois si les paramètres « libres » pré-spécifiés ne sont pas nuls, et inversement si les autres relations dans les données - celles que nous n’avons pas spécifiées dans le modèle - peuvent être considérées à zéro.
Figure 15‑30 : La fenêtre d’analyse CFA Jamovi
Comme pour l’AFC, Il existe plusieurs façons d’évaluer l’adéquation du modèle. La première est une statistique du chi carré, qui, si elle est petite, indique que le modèle est bien adapté aux données. Cependant, la statistique du chi carré utilisée pour évaluer l’ajustement du modèle est très sensible à la taille de l’échantillon, ce qui signifie qu’avec un grand échantillon (plus de 300-400 cas), un ajustement suffisamment bon entre le modèle et les données produit presque toujours une valeur importante et significative du chi carré.
Nous avons donc besoin d’autres moyens d’évaluer l’adéquation du modèle. Dans Jamovi plusieurs sont fournis par défaut. Il s’agit de l’indice d’ajustement comparatif (CFI), de l’indice d’ajustement Tucker (TFI) et de l’erreur quadratique moyenne quadratique approximative (RMSEA) ainsi que de l’intervalle de confiance à 90 % pour la RMSEA. Comme nous l’avons mentionné précédemment, certaines règles empiriques utiles sont qu’un ajustement satisfaisant est indiqué par CFI > 0,9, TFI > 0,9, et RMSEA compris entre 0,05 à 0,08. Un bon ajustement est CFI > 0.95, TFI ą 0.95, et RMSEA et CI supérieur pour RMSEA < 0.05.
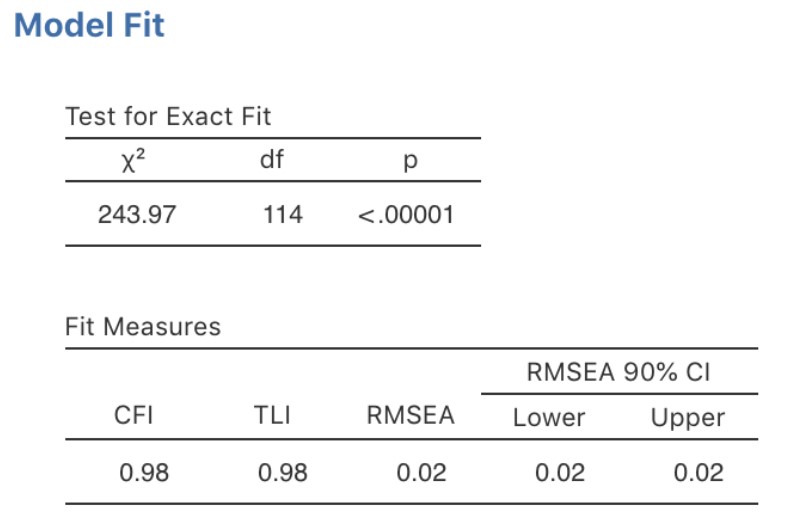
Ainsi, en regardant la Figure 15‑31, on constate que la valeur du chi carré est très significative, ce qui n’est pas surprenant étant donné la grande taille de l’échantillon (N=2748). La CFI est de 0,98 et l’indice TFI est également de 0,98, ce qui indique un très bon ajustement. La RMSEA est de 0,02 avec un intervalle de confiance de 90 % de 0,02 à 0,02 - est assez étroit !
Dans l’ensemble, je pense que nous pouvons être satisfaits que notre modèle pré-spécifié correspond très bien aux données observées, ce qui appuie notre modèle MTMM pour l’ASQ.
Figure 15‑31 : Résultats de l’ajustement de notre modèle d’AFC MTMM dans Jamovi
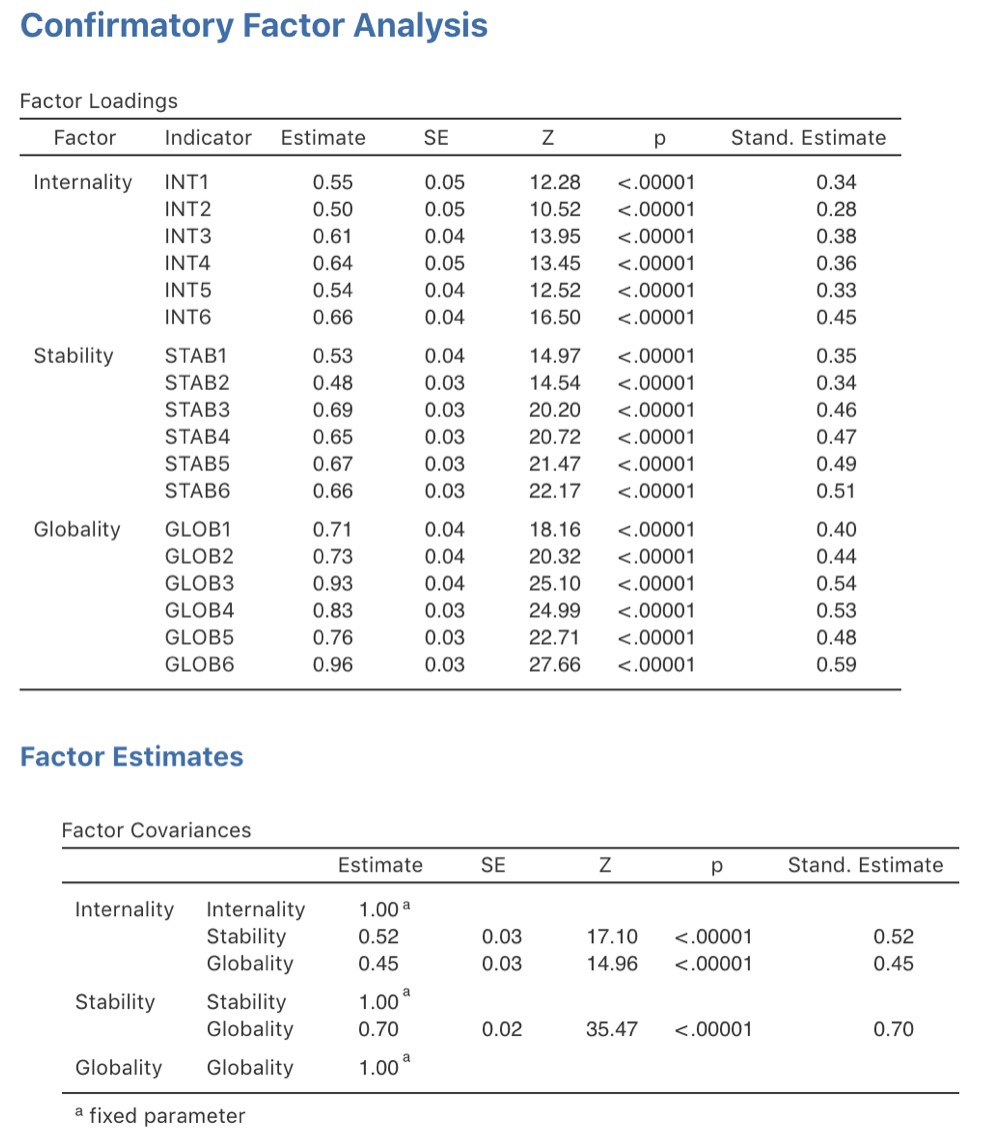
Nous pouvons maintenant examiner les saturations factorielles et les estimations de la covariance des facteurs, comme dans la Figure 15‑32.
Souvent, les estimations normalisées sont plus faciles à interpréter, et elles peuvent être précisées dans l’option « Estimates «. Ces tableaux peuvent utilement être incorporés dans un rapport écrit ou un article scientifique.
Vous pouvez voir à la Figure 15‑32 que toutes nos saturations factorielles et covariances factorielles préétablies sont significativement différentes de zéro. En d’autres termes, ils semblent tous apporter une contribution utile au modèle.
Nous avons eu beaucoup de chance avec cette analyse, en obtenant un très bon ajustement lors de notre première tentative. C’est assez inhabituel, et souvent, dans l’AFC, des ajustements post hoc supplémentaires sont apportés au modèle pour en améliorer l’ajustement. Une façon d’y parvenir est d’utiliser des « indices de modification » (MI), en les demandant dans « Additionnal Outputs » dans Jamovi.
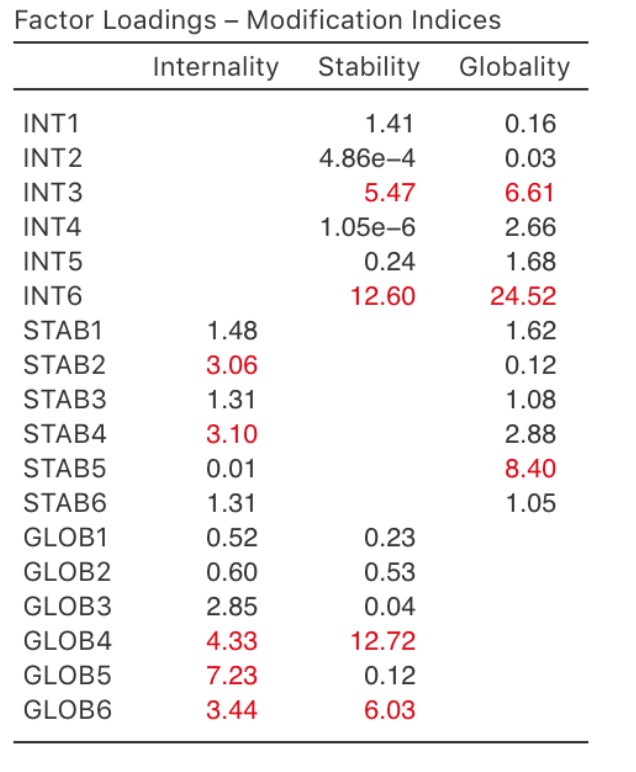
Ce que nous recherchons, c’est la valeur la plus élevée de l’indice de modification (MI). Nous jugerions alors s’il est judicieux d’ajouter ce terme supplémentaire dans le modèle, en utilisant une analyse post-hoc. Par exemple, nous pouvons voir à la Figure 15‑33 que le MI le plus élevé pour les charges factorielles qui ne sont pas déjà dans le modèle est une valeur de 24,52 pour la charge de INT6 sur le facteur latent Globalité. Cela indique que si nous ajoutons ce chemin dans le modèle, la valeur du khi-carré diminuera d’environ 25. Mais dans notre modèle, l’ajout de cette relation n’a pas vraiment de sens théorique ou méthodologique, et nous n’inclurons donc pas cette relation dans un modèle révisé.
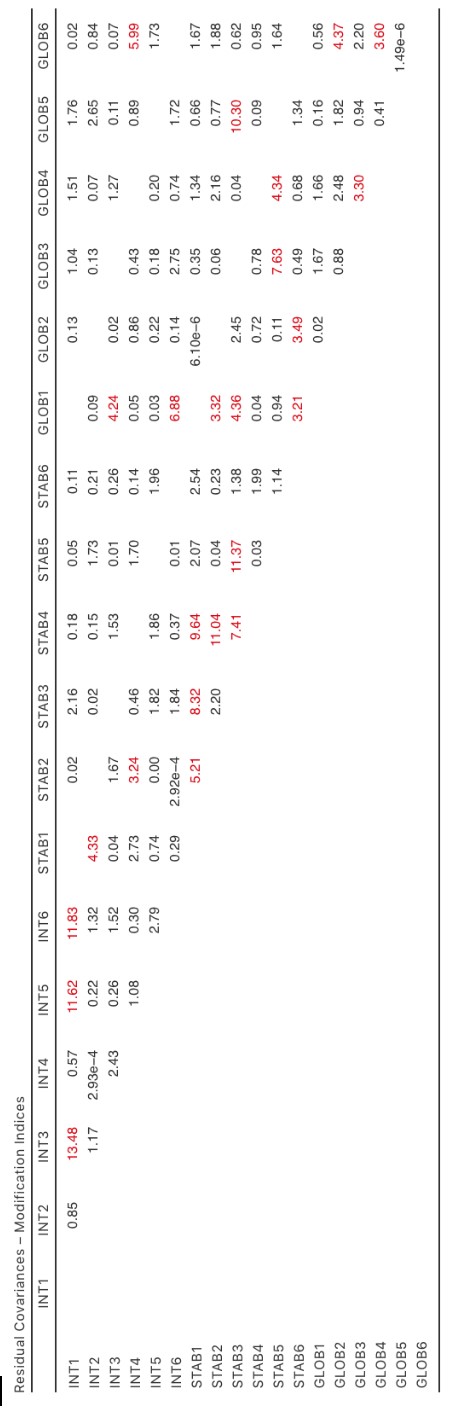
De même, lorsque nous examinons les MI des termes résiduels (Figure 15‑34), le MI le plus élevé qui permet aux erreurs entre INT1 et INT3 de varier (c’est-à-dire d’être incluses dans le modèle) est de 13,48 Ce n’est pas un MI élevé, il n’y a donc pas de justification raisonnable pour inclure ce paramètre dans le modèle, et nous avons déjà un bon ajustement, donc encore une fois notre réponse est de ne pas faire de modification.
Si vous ajoutez de nouveaux paramètres à un modèle à l’aide d’un MI, vérifiez toujours les tables de MI après chaque nouvel ajout (ou exclusion - un MI peut également suggérer des paramètres à supprimer d’un modèle pour améliorer l’ajustement du modèle), car les indicateurs sont actualisés chaque fois.
15.5 Analyse de la fiabilité de la cohérence interne
Après avoir suivi le processus initial d’élaboration de l’échelle à l’aide de l’AFE et de l’AFC, vous devriez avoir atteint un stade où l’échelle résiste assez bien à l’AFC avec différents échantillons. Vous pourriez également être intéressé à cette étape de voir comment les facteurs sont mesurés à l’aide d’une échelle qui combine les variables observées.
En psychométrie, nous utilisons l’analyse de fiabilité pour fournir de l’information sur l’uniformité avec laquelle une échelle mesure une construction psychologique (voir la section 2.3). La cohérence interne est ce qui nous intéresse ici, c’est-à-dire la cohérence entre tous les éléments qui composent une échelle de mesure. Ainsi, si nous avons V1, V2, V3, V4 et V5 comme variables d’élément observées, nous pouvons calculer une statistique qui nous indique dans quelle mesure ces éléments sont cohérents sur le plan interne dans la mesure du concept sous-jacent.
Une statistique populaire utilisée pour vérifier la cohérence interne d’une échelle est l’alpha de Cronbach (Cronbach 1951). L’alpha de Cronbach est une mesure d’équivalence (c.-à-d. teste si différents ensembles de mesures donnent les mêmes résultats). L’équivalence est testée en divisant les éléments de l’échelle en deux groupes (a « split-half ») et en vérifiant si l’analyse des deux parties donne des résultats comparables.
Figure 15‑32 : les tableaux des saturations et des covariances des facteur de l’AFC dans Jamovi avec notre modèle MTMM.
Bien sûr, il existe de nombreuses façons de fractionner un ensemble d’items, mais si tous les fractionnements possibles sont effectués, il est possible de produire une statistique qui reflète le modèle global des coefficients. L’alpha de Cronbach est une telle statistique : une fonction de tous les coefficients de demi-échelle pour une échelle. En même temps, vous pouvez également doubement vérifier si la suppression d’un élément de l’échelle améliore ma fiabilité.
Figure 15‑33 : Indices de modification des charges des facteurs CFA Jamovi
Si un ensemble d’éléments mesurant une construction (p. ex. une échelle d’extraction) a un alpha de 0,80, alors la proportion de variance d’erreur dans l’échelle est de 0,20. En d’autres termes, une échelle avec un alpha de 0,80 comprend environ 20 % d’erreur.
MAIS, (et c’est un GRAND « MAIS »), l’alpha de Cronbach n’est pas une mesure d’unicité (c’est-à-dire un indicateur qu’une échelle mesure un facteur ou une construction unitaire plutôt que plusieurs constructions connexes). Les échelles multidimensionnelles entraîneront une sous-estimation de l’alpha si elles ne sont pas évaluées séparément pour chaque dimension, mais des valeurs élevées pour l’alpha ne sont pas nécessairement des indicateurs d’unicité. Ainsi, un alpha de 0,80 ne signifie pas que 80 % d’une seule construction sous-jacente est prise en compte. Il se peut que les 80 % proviennent de plus d’une construction sous-jacente. C’est pourquoi il est utile de faire avant une AFE et une AFC sont utiles.
Figure 15‑34 : Indices de modification des covariances résiduelles CFA Jamovi
De plus, une autre caractéristique de l’alpha est qu’il a tendance à être spécifique à l’échantillon : ce n’est pas une caractéristique de l’échelle, mais plutôt une caractéristique de l’échantillon dans lequel l’échelle a été utilisée. Un échantillon biaisé, non représentatif ou de petite taille pourrait produire un coefficient alpha très différent de celui d’un grand échantillon représentatif. L’alpha peut même varier d’un grand échantillon à l’autre. Néanmoins, malgré ces limites, l’alpha de Chronbach est très populaire en psychologie pour l’estimation de la fiabilité de la cohérence interne pour les raisons suivantes. Il est assez facile à calculer, à comprendre et à interpréter, et par conséquent, il peut s’agir d’une vérification initiale utile de la précision de la mesure lorsque vous administrez une échelle avec un échantillon différent, par exemple dans un autre milieu ou une population différents
Une alternative est Omega de McDonald, et Jamovi fournit également cette statistique. Alors que l’alpha fait les hypothèses suivantes : (a) aucune corrélation résiduelle, (b) les items ont des saturations identiques, et (c) l’échelle est unitire, l’omega ne les fait pas et est donc une statistique de fiabilité plus robuste. Si ces hypothèses ne sont pas violées, l’alpha et l’oméga seront similaires, mais si elles le sont, alors il faut privilégier l’omega.
Parfois, un seuil pour l’alpha est fourni, ce qui suggère une valeur « suffisante ». Il pourrait s’agir d’alphas de 0,70 ou 0,80 représentant respectivement une fiabilité « acceptable » et « bonne ». Cependant, cela dépend de ce que l’échelle est censée mesurer exactement, de sorte que des seuils comme celui-ci doivent être utilisés avec prudence. Il pourrait être préférable d’indiquer simplement qu’un alpha de 0,70 est associé à une variance d’erreur de 30 % dans une échelle, et qu’un alpha de 0,80 est associé à 20 %.
L’alpha peut-il être trop élevé ? Probablement : si vous obtenez un coefficient alpha supérieur à 0,95, cela indique des corrélations élevées entre les éléments et qu’il peut y avoir trop de spécicités redondantes dans la mesure, avec un risque que la construction mesurée soit peut-être trop restreinte.
15.5.1 Analyse de la fiabilité dans Jamovi
Nous disposons d’un troisième ensemble de données pour entreprendre une analyse de fiabilité : le fichier bfi_sample3.csv. Une fois de plus, vérifiez que les 25 variables de personnalité sont codées comme continues. Pour effectuer des analyses de fiabilité dans Jamovi :
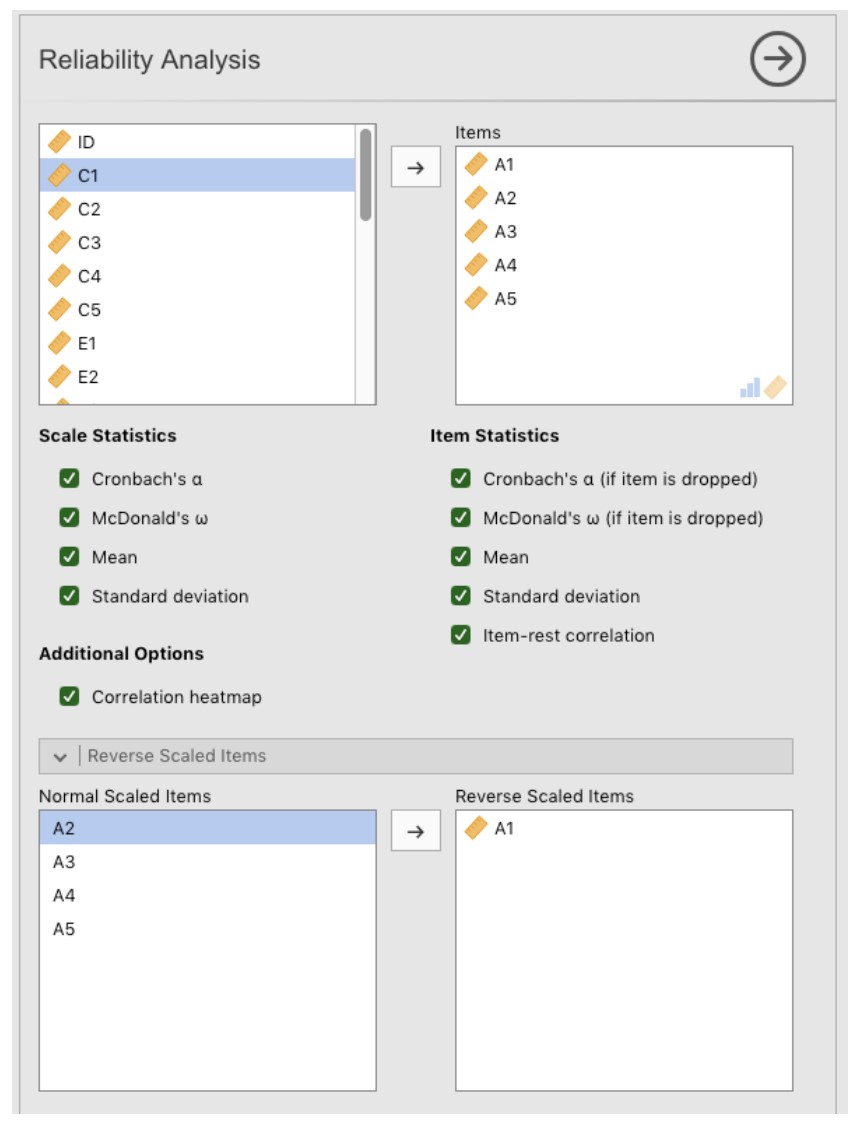
Sélectionnez Factor - Reliability Analysis dans la barre principale de boutons de Jamovi pour ouvrir la fenêtre d’analyse de fiabilité (Figure 15‑35).
Sélectionnez les 5 variables A et transférez-les dans la boîte « Items ».
Sous l’option « Reverse Scaled Items », sélectionnez la variable A1 dans la case « Normal Scaled Items » et déplacez-la dans la case « Reverse Scaled Items ».
Cochez les autres options appropriées, comme dans la Figure 15‑35.
Figure 15‑35 : Fenêtre Analyse de fiabilité Jamovi
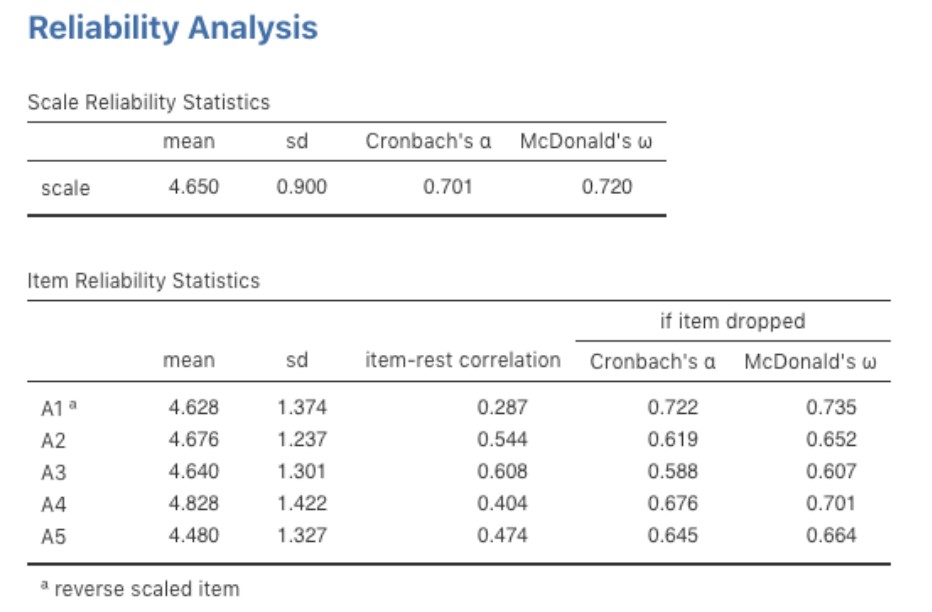
Une fois fait, regardez la fenêtre des résultats de Jamovi. Vous devriez voir quelque chose comme Figure 15‑36. Cela nous indique que le coefficient alpha de Chronbach pour l’échelle de Agreeableness est de 0,70. Cela signifie qu’un peu moins de 30 % de la note de l’échelle Agreeableness représente la variance d’erreur. L’Oméga de McDonald est aussi fourni, et il est de 0,72, ce qui n’est pas très différent de l’alpha.
Nous pouvons également vérifier comment l’alpha ou l’oméga peut être amélioré avec la suppression d’un élément spécifique. Par exemple, l’alpha passerait à 0,72 et l’oméga à 0,74 si nous supprimions le point A1. Il ne s’agit pas d’une augmentation importante, donc cela ne vaut probablement pas la peine d’être fait.
Le processus de calcul et de vérification des statistiques de fiabilité (alpha et oméga) est le même pour toutes les autres échelles (non représentées) : Conscientiousness (alpha = 0,73, oméga = 0,74), Extraversion (alpha = 0,76, oméga = 0,76), Neuroticism (alpha = 0,81, oméga = 0,82) et Openness (alpha = 0,60, oméga = 0,62). Pour l’ouverture, la variance d’erreur dans le score de l’échelle est de 40 %, ce qui est élevé et indique que l’ouverture est beaucoup moins cohérente comme mesure fiable d’un attribut de personnalité que les autres échelles de personnalité.
Figure 15‑36 : Résultats de l’analyse de fiabilité de Jamovi pour le facteur Agreeableness
15.6 Résumé
L’analyse factorielle exploratoire (AEF) est une technique statistique permettant d’identifier les facteurs latents sous-jacents d’un ensemble de données. Chaque variable observée est conceptualisée comme représentant dans une certaine mesure le facteur latent, indiqué par une saturation factorielle. Les chercheurs utilisent également l’AEF comme moyen de réduire les données, c’est-à-dire d’identifier les variables observées qui peuvent être combinées en de nouvelles variables pour une analyse ultérieure. (Section 15.1)
L’analyse en composantes principales (ACP) est une technique de réduction des données qui, à proprement parler, n’identifie pas les facteurs latents sous-jacents. Au lieu de cela, l’ACP produit simplement une combinaison linéaire de variables observées. (Section 15.2)
Analyse factorielle de confirmation (AFC). Contrairement à l’AFE, avec l’AFC, vous commencez par une idée - un modèle - de relations entre vos variables observées. Vous testez ensuite votre modèle par rapport aux données observées et évaluez dans quelle mesure il s’adapte au modèle. (Section 15.3)
Dans l’AFC multitraits multiméthodes (MTMM), la variance du facteur latent et la variance de la méthode sont incluses dans le modèle dans une approche qui est utile lorsqu’il y a différentes approches méthodologiques utilisées et que la variance de la méthode est donc une considération importante (section 15.4).
Analyse de fiabilité de la cohérence interne. Cette forme d’analyse de fiabilité teste la cohérence d’une échelle pour la mesure d’une mesure consruite (psychologique). (Section 15.5)
References
Cronbach, Lee J. 1951. “Coefficient Alpha and the Internal Structure of Tests.” Psychometrika 16 (3): 297–334. https://doi.org/10.1007/BF02310555.
Hewitt, Anthea K., David R. Foxcroft, and John MacDonald. 2004. “Multitrait-Multimethod Confirmatory Factor Analysis of the Attributional Style Questionnaire.” Personality and Individual Differences 37 (7): 1483–91. https://doi.org/10.1016/j.paid.2004.02.005.
Peterson, Christopher, and Martin E P Seligman. 1984. “Causal Explanations as a Risk Factor for Depression: Theory and Evidence,” 28.
Les saturations factorielles peuvent être interprétées comme des coefficients de régression normalisés, ce qui est très utile↩︎
Une valeur propre indique dans quelle mesure la variance des variables observées est prise en compte par un facteur. Un facteur avec une valeur propre > 1 explique plus de variance qu’une seule variable observée.↩︎
NdT : j’ai retenu ici le terme proposé par l’ISI glossary (http://isi.cbs.nl/glossary/term3435.htm) pour traduire uniqueness↩︎
Dans l’analyse factorielle, le terme « communauté » ou « varaiance commune » est parfois utilisé pour désigner le degré de variance d’une variable qui est pris en compte par la solution factorielle. L’unicité est égale à (1 - communauté)↩︎
… et cela signifie qu’il y a beaucoup de répétitions dans les étapes de l’ACP décrites dans la section suivante. J’en suis et espère que cela conviendra !↩︎
Soit dit en passant, étant donné que nous avions une idée assez précise de nos facteurs « supposés » initiaux, nous aurions simplement pu passer directement à l’AFC et sauter l’étape de l’AFE. La question de savoir si vous utilisez l’AFE et passez ensuite à l’AFC, ou si vous passez directement à l’AFC, est une question de jugement et de confiance dans le fait que vous avez initialement la structure adéquate (en termes de nombre de facteurs et de variables). Au début de l’élaboration des échelles ou pour l’identification des constructions latentes sous-jacentes, les chercheurs ont tendance à utiliser l’AFE. Ensuite, lorsqu’ils se rapprochent d’une échelle finale, ou s’ils veulent vérifier une échelle établie avec un nouvel échantillon, alors l’AFC est une bonne option.↩︎