Chapitre 4 Statistiques descriptives
Chaque fois que vous obtenez un nouveau jeu de données à examiner, l’une des premières tâches que vous avez à faire est de trouver des moyens de résumer les données d’une manière synthétique et facile à comprendre. C’est à cela que servent les statistiques descriptives (par opposition aux statistiques inférentielles). En fait, pour beaucoup de gens, le terme « statistiques » est synonyme de statistiques descriptives. C’est ce sujet que nous allons aborder dans ce chapitre, mais avant d’entrer dans les détails, prenons un moment pour comprendre pourquoi nous avons besoin de statistiques descriptives. Pour ce faire, ouvrons le fichier aflsmall margins et voyons quelles variables sont stockées dans le fichier.
Figure 4‑1 Une capture d’écran de Jamovi montrant les variables stockées dans le fichier aflsmal_margins.csv
En fait, il n’y a qu’une seule variable ici, les afl.margins Nous allons nous concentrer un peu sur cette variable dans ce chapitre et je vais préciser de quoi il s’agit. Contrairement à la plupart des ensembles de données de ce livre, il s’agit en fait de données réelles, relatives à la Ligue australienne de football (AFL).20 La variable afl.margins contient la marge gagnante (nombre de points) pour les 176 matchs joués à domicile et à l’extérieur durant la saison 2010.
Ce résultat ne permet pas de se faire une idée de ce que les données disent réellement. Le simple fait de « regarder les données » n’est pas une façon très efficace de comprendre les données. Afin d’avoir une idée de ce que les données nous disent réellement, nous devons calculer quelques statistiques descriptives (ce chapitre) et dessiner quelques belles images (chapitre 5). Puisque les statistiques descriptives sont le plus facile des deux sujets, je vais commencer par celles-ci, cependant je vais vous montrer un histogramme des données afl.margins puisqu’il devrait vous aider à avoir une idée de ce à quoi ressemblent les données que nous essayons de décrire, (voir Figure 4‑2). Nous parlerons plus en détail de la façon de dessiner des histogrammes dans la section 5.1. Pour l’instant, il suffit de regarder l’histogramme et de noter qu’il fournit une représentation assez interprétable des données des marges afl.
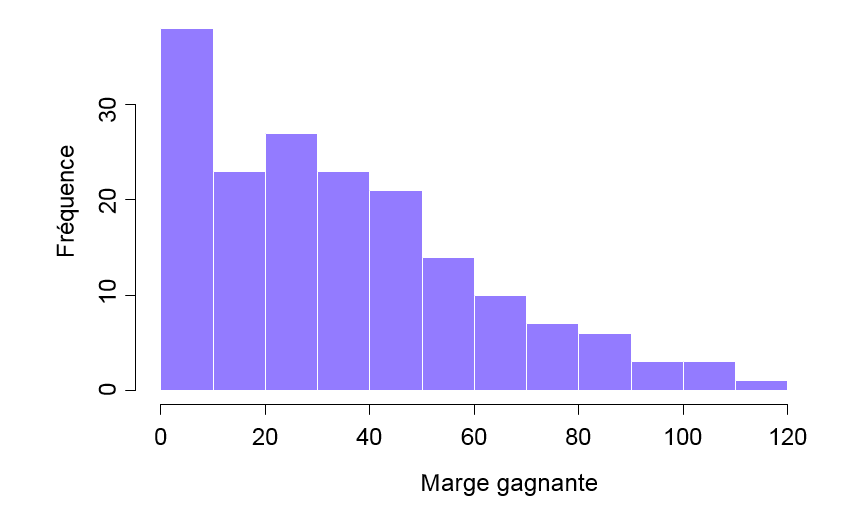
Figure 4‑2 : Un histogramme des données de la marge gagnante AFL 2010 (la variable afl.margins). Comme vous pouvez vous y attendre, plus la marge gagnante est grande, moins vous avez tendance à la voir fréquemment.
4.1 Mesures de la tendance centrale
Dessiner des graphiques des données, comme je l’ai fait dans la Figure 4‑2, est une excellente façon de donner un aperçu de ce que les données tentent de vous dire. Il est souvent extrêmement utile d’essayer de condenser les données en quelques statistiques « sommaires » simples. Dans la plupart des situations, la première chose que vous voudrez calculer est une mesure de la tendance centrale. En d’autres termes, vous aimeriez savoir où se situe la « moyenne » ou le « milieu » de vos données. Les trois mesures les plus couramment utilisées sont la moyenne, la médiane et le mode. J’expliquerai chacun d’eux à tour de rôle, puis je discuterai de l’utilité de chacun d’entre eux.
4.1.1 La moyenne
La moyenne d’un ensemble d’observations n’est qu’une moyenne normale et classique. Additionnez toutes les valeurs, puis divisez-les par le nombre total de valeurs. Les cinq premières marges gagnantes de l’AFL étaient 56, 31, 56, 8 et 32, de sorte que la moyenne de ces observations est juste :
\[ \frac{56 + 31 + 56 + 8 + 32}{5} = \frac{183}{5} = 36,60 \]
Bien sûr, cette définition de la moyenne n’est nouvelle pour personne. Les valeurs moyennes (c.-à-d. les moyennes) sont utilisées si souvent dans la vie de tous les jours que cela en fait d’une notion assez familière. Cependant, comme le concept de moyenne est quelque chose que tout le monde comprend déjà, je vais m’en servir comme excuse pour commencer à introduire une partie de la notation mathématique que les statisticiens utilisent pour décrire ce calcul, et parler de la façon dont les calculs seraient effectués dans Jamovi.
La première notation à introduire est N, que nous utiliserons pour faire référence au nombre d’observations que nous faisons la moyenne (dans ce cas N = 5). Ensuite, nous devons apposer une étiquette sur les observations elles-mêmes. Il est traditionnel d’utiliser X pour cela, et d’utiliser des indices pour indiquer de quelle observation il s’agit. C’est-à-dire, nous utiliserons X1 pour faire référence à la première observation, X2 pour faire référence à la deuxième observation, et ainsi de suite jusqu’à XN pour la dernière. Ou, pour dire la même chose d’une manière un peu plus abstraite, nous utilisons Xi pour faire référence à la i-ème observation. Juste pour être sûr d’être clair sur la notation, le tableau suivant énumère les 5 observations de la variable afl.margins, ainsi que le symbole mathématique utilisé pour s’y référer et la valeur réelle à laquelle l’observation correspond :
Bien, maintenant essayons d’écrire une formule pour la moyenne. Par tradition, nous utilisons \(\bar{X}\) comme notation de la moyenne. Le calcul de la moyenne pourrait donc être exprimé à l’aide de la formule suivante :
\[ \bar{X} = \frac{X_{1} + X_{2} + X_{2} + \ldots X_{N - 1} + X_{N}}{N} \]
Cette formule est tout à fait correcte, mais elle est terriblement longue, c’est pourquoi nous utilisons le symbole de sommation \(\sum\) pour la raccourcir21. Si je veux additionner les cinq premières observations, je pourrais écrire la somme de façon longue, X1 + X2 + X3 + X4 + X5 ou je pourrais utiliser le symbole de somme pour l’abréger comme ceci :
\[ \sum_{i = 1}^{5}X_{i} \]
Prise littéralement, cela pourrait se lire comme « la somme, prise sur toutes les i valeurs de 1 à 5, de la valeur Xi ». Mais au fond, cela signifie qu’il faut « additionner les cinq premières observations ». Dans tous les cas, nous pouvons utiliser cette notation pour écrire la formule de la moyenne, qui ressemble à ceci :
\[ \bar{X} = \frac{1}{N}\sum_{i = 1}^{N}X_{i} \]
En toute honnêteté, je ne peux pas imaginer que toute cette notation mathématique aide à clarifier le concept de moyenne. En fait, c’est juste une façon d’écrire la même chose que ce que j’ai dit avec des mots : additionnez toutes les valeurs, puis divisez-les par le nombre total d’éléments. Cependant, ce n’est pas vraiment la raison pour laquelle je suis entré dans tous ces détails. Mon but était d’essayer de m’assurer que tous ceux qui lisent ce livre soient clairs sur la notation que nous utiliserons tout au long du livre : \(\bar{X}\) pour la moyenne, \(\sum\) pour l’idée de sommation, \(X_{i}\) pour la i-ème observation et N pour le nombre total d’observations. Nous allons réutiliser ces symboles un peu, alors il est important que vous les compreniez assez bien pour pouvoir « lire » les équations et voir qu’il s’agit simplement de dire « additionnez beaucoup de choses et divisez-les par une autre chose ».
4.1.2 Calcul de la moyenne avec Jamovi
Bien, c’est des maths. Alors, comment pouvons-nous obtenir que la boîte informatique magique fasse le travail pour nous ? Lorsque le nombre d’observations commence à augmenter, il est beaucoup plus facile d’effectuer ce genre de calcul à l’aide d’un ordinateur. Pour calculer la moyenne en utilisant toutes les données, nous pouvons utiliser Jamovi. La première étape consiste à cliquer sur le bouton « Exploration », puis sur « Descriptives ». Ensuite, vous pouvez mettre en surbrillance la variable afl.margins et cliquer sur la flèche vers la droite pour la déplacer dans la boîte « Variables ». Après avoir fait cela, un tableau apparaît sur le côté droit de l’écran contenant les informations par défaut « Descriptives » ; voir Figure 4‑3.
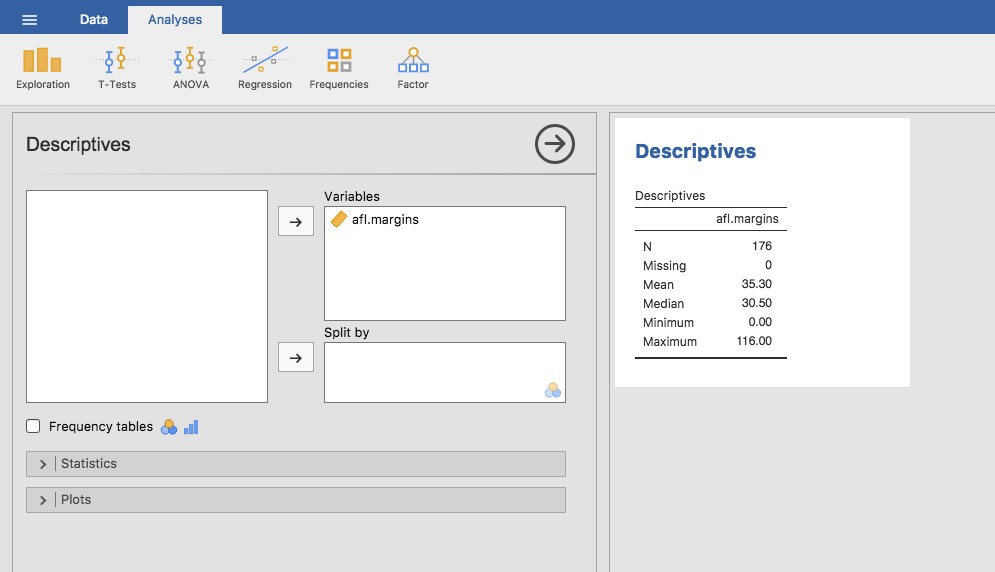
Figure 4‑3 Descriptifs par défaut des données de la marge gagnante AFL 2010 (la variable afl.margins).
Comme vous pouvez le voir à la Figure 4‑3, la valeur moyenne de la variable afl.margins est de 35,30. Les autres renseignements présentés comprennent le nombre total d’observations (N=176), le nombre de valeurs manquantes (aucune) et les valeurs médiane, minimale et maximale pour la variable.
4.1.3 La médiane
La deuxième mesure de la tendance centrale que les gens utilisent beaucoup est la médiane, et elle est encore plus facile à décrire que la moyenne. La médiane d’un ensemble d’observations n’est que la valeur centrale. Comme auparavant, imaginons que nous n’étions intéressés que par les 5 premières marges gagnantes de l’AFL : 56, 31, 56, 8 et 32. Pour déterminer la médiane, nous trions ces nombres par ordre croissant :
8,31,32,56,56
En inspectant les données, il est évident que la valeur médiane de ces 5 observations est de 32 puisque c’est celle du milieu dans la liste triée (je l’ai mise en gras pour la mettre en évidence). C’est facile. Mais que faire si nous sommes intéressés par les 6 premiers jeux plutôt que par les 5 premiers ? Puisque le sixième match de la saison avait une marge gagnante de 14 points, notre liste triée est maintenant la suivante :
8,14,31,32,56,*56
et il y a deux nombres intermédiaires, 31 et 32. La médiane est définie comme la moyenne de ces deux nombres, qui est bien sûr de 31,5. Comme auparavant, c’est très fastidieux de le faire à la main quand on a beaucoup de chiffres. Dans la vraie vie, bien sûr, personne ne calcule réellement la médiane en triant les données et en cherchant ensuite la valeur moyenne. Dans la vraie vie, nous utilisons un ordinateur pour faire le travail pénible pour nous, et Jamovi nous a fourni une valeur médiane de 30,50 pour la variable afl.margins (Figure 4‑3).
4.1.4 Moyenne ou médiane ? Quelle est la différence ?
Savoir calculer les moyennes et les médianes n’est qu’une partie de l’histoire. Vous devez également comprendre ce que chacun dit au sujet des données, et ce que cela implique au moment où vous devez utiliser chacune d’elles. C’est ce qu’illustre la Figure 4‑4. La moyenne est un peu comme le « centre de gravité » de l’ensemble de données, alors que la médiane est la « valeur centrale » des données. Ce que ceci implique, pour ce qui est de savoir lequel vous devriez utiliser, dépend un peu du type de données que vous possédez et de ce que vous essayez de faire. A titre indicatif :
Si vos données sont dans une échelle nominale, vous ne devriez probablement pas utiliser la moyenne ou la médiane. La moyenne et la médiane reposent toutes deux sur l’idée que les nombres attribués aux valeurs sont significatifs. Si la numérotation est arbitraire, il est probablement préférable d’utiliser le mode (Section 4.1.6) à la place.
Si vos données sont sur une échelle ordinale, vous êtes plus susceptible de privilégier la médiane que la moyenne. La médiane n’utilise que les informations de classement de vos données (c’est-à-dire les chiffres les plus grands) mais ne dépend pas des nombres précis en cause. C’est exactement la situation qui s’applique lorsque vos données sont à l’échelle ordinale. La moyenne, par contre, utilise les valeurs numériques précises attribuées aux observations, donc elle n’est pas vraiment appropriée pour les données ordinales.
Pour les données de l’échelle d’intervalles et de rapport, l’une ou l’autre est généralement acceptable. Le choix de celui que vous choisissez dépend un peu de ce que vous essayez de faire. La moyenne a l’avantage d’utiliser toute l’information contenue dans les données (ce qui est utile lorsque vous n’avez pas beaucoup de données). Mais elle est très sensible aux valeurs extrêmes et marginales.
Développons un peu cette dernière partie. L’une des conséquences est qu’il existe des différences systématiques entre la moyenne et la médiane lorsque l’histogramme est asymétrique (asymétrique ; voir section 4.3). C’est ce qu’illustre la Figure 4‑4 Notez que la médiane (côté droit) est située plus près du « corps » de l’histogramme, alors que la moyenne (côté gauche) est traînée vers la « queue » (où se trouvent les valeurs extrêmes). Pour donner un exemple concret, supposons que Robert (revenu de 50 000 $), Kate (revenu de 60 000 $) et Jeanne (revenu de 65 000 $) sont assis à une table. Le revenu moyen à la table est de 58 333 $ et le revenu médian est de 60 000 $. Puis Bill s’assoit avec eux (revenu de 100 000 000 $). Le revenu moyen est maintenant passé à 25 043 750 $, mais la médiane n’est que de 62 500 $. Si vous voulez examiner le revenu global à la table, la moyenne pourrait être la bonne réponse. Mais si vous vous intéressez à ce qui est considéré comme un revenu typique à la table, la médiane serait un meilleur choix ici.
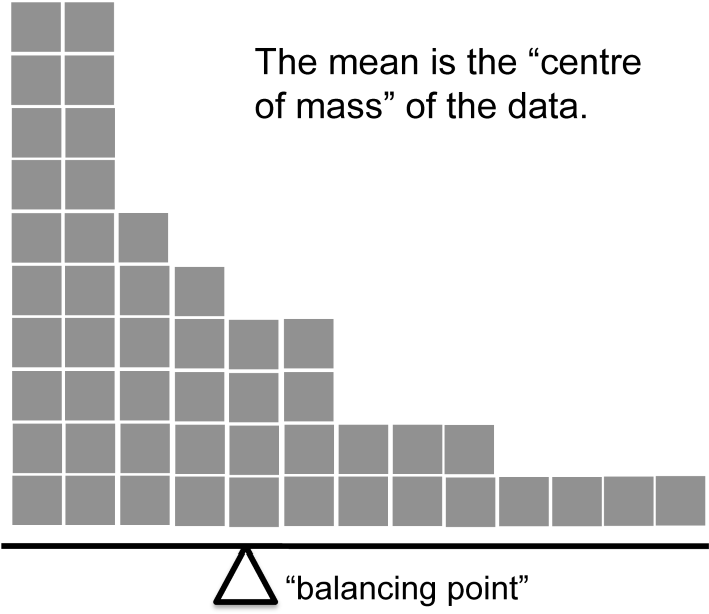
Figure 4‑4 : Une illustration de la différence entre l’interprétation de la moyenne et celle de la médiane. La moyenne est essentiellement le « centre de gravité » de l’ensemble de données. Si vous imaginez que l’histogramme des données est un objet solide, alors le point sur lequel vous pouvez l’équilibrer (comme sur une bascule) est la moyenne. Par contre, la médiane est l’observation du milieu, la moitié des observations étant plus petites et la moitié plus grandes.
4.1.5 Un exemple concret
Pour essayer de comprendre pourquoi vous devez prêter attention aux différences entre la moyenne et la médiane, considérons un exemple réel. Comme j’ai tendance à me moquer des journalistes pour leurs faibles connaissances scientifiques et statistiques, je dois rendre à César ce qui est à César. Voici un excellent article sur le site d’ABC news22 du 24 septembre 2010 :
Au cours des deux dernières semaines, des cadres supérieurs de la Commonwealth Bank ont parcouru le monde avec une présentation montrant que les prix des maisons en Australie et les principaux ratios prix-revenus se comparent avantageusement à ceux de pays similaires. « En fait, l’accessibilité à la propriété a dérapé au cours des cinq ou six dernières années », a déclaré Craig James, économiste en chef de la division commerciale de la banque, CommSec.
C’est probablement une énorme surprise pour quiconque a un prêt hypothécaire, ou qui veut un prêt hypothécaire, ou qui paie un loyer, ou qui n’est pas complètement inconscient de ce qui se passe sur le marché australien du logement depuis plusieurs années. Retournons à l’article :
L’ABC a mené sa guerre contre ce qu’elle croit être des prophètes de malheur avec des graphiques, des chiffres et des comparaisons internationales. Dans sa présentation, la banque rejette les arguments selon lesquels le logement en Australie est relativement cher par rapport aux revenus. Il indique que le ratio du prix des maisons par rapport au revenu des ménages, qui est de 5,6 dans les grandes villes et de 4,3 à l’échelle nationale, est comparable à celui de nombreux autres pays développés. Il est dit que San Francisco et New York ont des ratios de 7, Auckland est à 6,7 et Vancouver à 9,3.
Encore une excellente nouvelle ! Sauf que l’article poursuit en disant que :
De nombreux analystes disent que cela a conduit la banque à utiliser des chiffres trompeurs et des comparaisons. Si vous allez à la page 4 de l’exposé de l’ABC et que vous lisez l’information de la source au bas du graphique et du tableau, vous remarquerez qu’il y a une autre source sur la comparaison internationale - Demographia. Toutefois, si la Commonwealth Bank avait également utilisé l’analyse de Demographia sur le ratio prix/revenu des maisons en Australie, elle aurait obtenu un chiffre plus proche de 9 plutôt que 5,6 ou 4,3.
C’est, euh, un écart assez sérieux. Un groupe de personnes dit 9, un autre dit 4-5. Devrions-nous simplement couper en deux la différence et dire que la vérité se situe quelque part entre les deux ? Absolument pas ! C’est une situation où il y a une bonne et une mauvaise réponse. La démographie est correcte, et la Banque du Commonwealth a tort. Comme le souligne l’article :
[Un] problème évident avec les chiffres des prix intérieurs de la Banque du Commonwealth par rapport au revenu est qu’elle compare les revenus moyens aux prix médians des maisons (contrairement aux chiffres démographiques qui comparent les revenus médians aux prix médians). La médiane est le point central, ce qui signifie que la moyenne est généralement plus élevée lorsqu’il s’agit des revenus et des prix des actifs, car elle inclut les revenus des personnes les plus riches de l’Australie. En d’autres termes, les chiffres de la Commonwealth Bank comptent le salaire de plusieurs millions de dollars de Ralph Norris du côté des revenus, mais pas sa maison (sans doute) très chère dans les chiffres du prix de l’immobilier, ce qui sous-estime le ratio prix/revenu des maisons pour les Australiens à revenu moyen.
Je n’aurais pas pu mieux dire. La façon dont Demographia a calculé le ratio est la bonne. La façon dont la Banque l’a fait est incorrecte. Quant à savoir pourquoi une organisation extrêmement sophistiquée sur le plan quantitatif, comme une grande banque, a commis une erreur aussi élémentaire, eh bien… Je ne peux pas le dire avec certitude puisque je n’ai aucune idée précise de ce qu’ils pensent. Mais l’article lui-même mentionne les faits suivants, qui peuvent ou non être pertinents :
En tant que premier prêteur immobilier australien, la Banque du Commonwealth a l’un des intérêts les plus importants dans la hausse des prix de l’immobilier. Elle possède en effet une grande partie des logements australiens en garantie de ses prêts immobiliers ainsi que de nombreux prêts aux petites entreprises.
Mon Dieu, mon Dieu.
4.1.6 Mode
Le mode d’un échantillon est très simple. C’est la valeur qui s’observe le plus fréquemment. Nous pouvons illustrer le mode en utilisant une variable AFL différente : qui a joué le plus de finales ? Ouvrez le fichier des petits finalistes aflsmall et jetez un coup d’œil à la variable afl.finalists, voir Figure 4‑5. Cette variable contient les noms des 400 équipes qui ont participé aux 200 matches de la phase finale disputés entre 1987 et 2010.
Ce que nous pourrions faire, c’est lire l’ensemble des 400 inscriptions et compter le nombre d’occasions où chaque nom d’équipe apparaît dans notre liste de finalistes, produisant ainsi un tableau de fréquence. Cependant, ce serait stupide et ennuyeux : exactement le genre de tâche pour laquelle les ordinateurs sont très doués. Alors utilisons Jamovi pour faire ça pour nous. Sous « Exploration » - « Descriptives », cliquez sur la petite case à cocher intitulée « Frequency table » et vous devriez obtenir quelque chose comme Figure 4‑6.
Maintenant que nous avons notre tableau de fréquence, nous pouvons le regarder et constater qu’au cours des 24 années pour lesquelles nous disposons de données, Geelong a participé à plus de finales que toute autre équipe. Ainsi, le mode des données des données afl.finalistes est « Geelong ». On constate que Geelong (39 finales) a disputé plus de finales que toute autre équipe au cours de la période 1987-2010. Il convient également de noter que dans le tableau des statistiques descriptives, aucun résultat n’est calculé pour la moyenne, la médiane, le minimum ou le maximum. C’est parce que la variable afl.finalists est une variable nominale et que cela n’a pas de sens de calculer ces valeurs.
Figure 4‑5 Une capture d’écran de Jamovi montrant la variable stockée dans le fichier aflsmall_finalists.csv
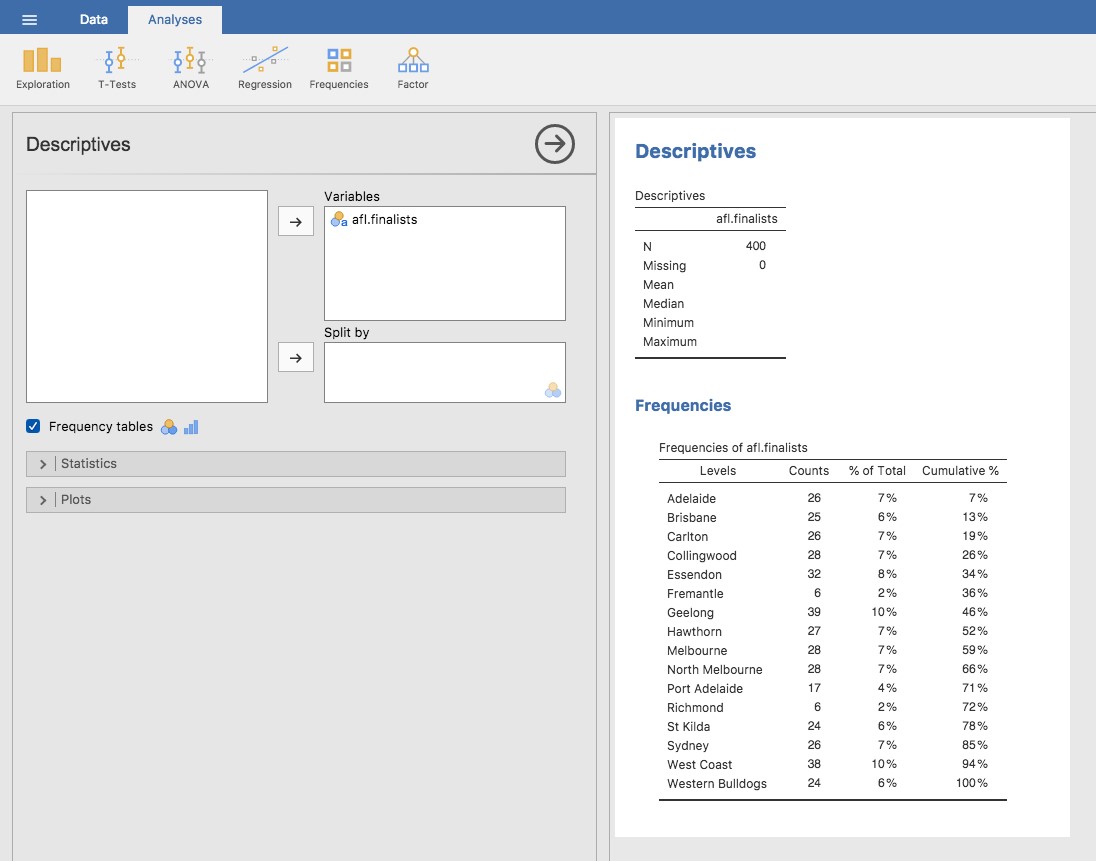
Figure 4‑6 : Une capture d’écran de Jamovi montrant la table de fréquence pour la variable afl.finalists
Une dernière remarque concernant le mode. Bien que le mode soit le plus souvent calculé lorsque vous disposez de données nominales, parce que les moyennes et les médianes sont inutiles pour ce genre de variables, il y a des situations dans lesquelles vous voulez vraiment connaître le mode d’une variable ordinale, d’intervalle ou de rapport. Par exemple, revenons à notre variable afl.margins. Cette variable est clairement une échelle de ratio (si vous ne comprenez pas bien, il peut être utile de relire la section 2.2) et, dans la plupart des cas, la moyenne ou la médiane est la mesure de la tendance centrale que vous voulez. Mais considérez ce scénario : un de vos amis propose un pari et il choisit un match de football au hasard. Sans savoir qui joue, vous devez deviner la marge de gain exacte. Si vous devinez correctement, vous gagnez 50 $. Si vous ne le faite pas, vous perdez 1 $, il n’y a pas de prix de consolation pour avoir « presque » obtenu la bonne réponse. Vous devez deviner exactement la bonne marge. Pour ce pari, la moyenne et la médiane vous sont complètement inutiles. C’est le mode sur lequel vous devriez parier. Pour calculer le mode de la variable afl.margins dans Jamovi, retournez à cet ensemble de données et sur l’écran « Exploration » -« Descriptives » vous verrez que vous pouvez développer la section marquée « Statistics». Cliquez sur la case à cocher « Mode » et vous verrez la valeur modale apparaitre dans le tableau « Descriptives », comme dans la Figure 4‑7. Les données de 2010 suggèrent donc que vous devriez miser sur une marge de 3 points.
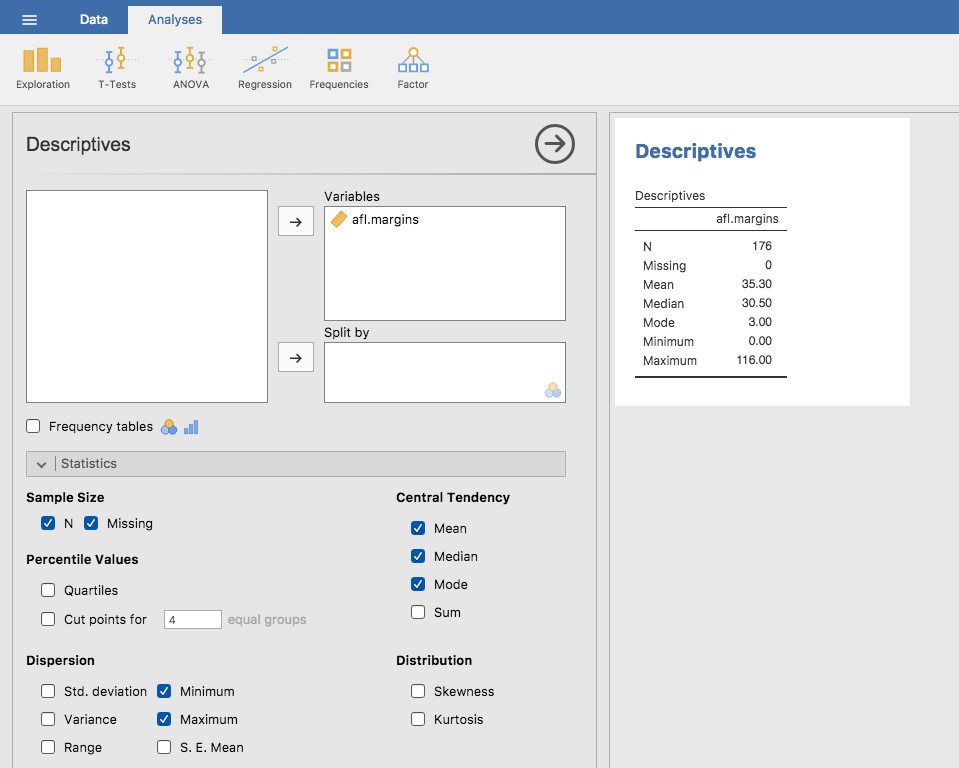
Figure 4‑7 : Une capture d’écran de Jamovi montrant la valeur modale de la variable afl.margins
4.2 Mesures de la variabilité
Les statistiques dont nous avons discuté jusqu’à présent portent toutes sur la tendance centrale. C’est-à-dire qu’ils parlent tous des valeurs qui sont « au milieu » ou « populaires » dans les données. Cependant, la tendance centrale n’est pas le seul type de statistique sommaire que nous voulons calculer. La deuxième chose que nous voulons vraiment, c’est une mesure de la variabilité des données. En d’autres termes, comment les données sont-elles « étalées » ? A quelle distance de la moyenne ou de la médiane les valeurs observées ont-elles tendance à être ? Pour l’instant, supposons que les données sont des échelles d’intervalles ou de ratios, et nous continuerons à utiliser les données de marges afl. Nous utiliserons ces données pour discuter de différentes mesures de propagation, chacune ayant des forces et des faiblesses différentes.
4.2.1 L’étendue
L’étendue d’une variable est très simple. C’est la plus grande valeur moins la plus petite valeur. Pour les données de marges gagnantes de l’AFL, la valeur maximale est de 116 et la valeur minimale est de 0. Bien que la plage soit le moyen le plus simple de quantifier la notion de « variabilité », c’est l’une des plus mauvaises. Rappelons-nous, dans notre discussion sur la moyenne, que nous voulons que notre mesure sommaire soit robuste. Si l’ensemble de données contient une ou deux valeurs extrêmement mauvaises, nous aimerions que nos statistiques ne soient pas indûment influencées par ces cas. Par exemple, dans une variable contenant des valeurs aberrantes très extrêmes
-100,2,3,4,5,6,7,8,9,10
Il est clair que l’étendue n’est pas robuste. Cette variable a une étendue de 110, mais si l’on supprimait la valeur aberrante, nous n’aurions qu’une étendue de 8.
4.2.2 Écart interquartile
L’écart interquartile (IQR) est comme l’écart, mais au lieu de la différence entre la plus grande et la plus petite valeur, on prend la différence entre le 25e et le 75e percentile. Si vous ne savez pas déjà ce qu’est un percentile, le 10e percentile d’un ensemble de données est le plus petit nombre x de sorte que 10 % des données sont inférieures à x. En fait, nous avons déjà trouvé l’idée. La médiane d’un ensemble de données est son 50e centile ! Dans Jamovi, vous pouvez facilement spécifier les 25e, 50e et 75e percentiles en cochant la case « Quartiles » dans l’écran « Exploration » « Descriptives » - « Statistics ».
Il n’est donc pas surprenant que, dans la Figure 4‑8, le 50e percentile soit le même que la valeur médiane. Et, en notant que 50,50 - 12,75 = 37,75, nous pouvons voir que l’écart interquartile des marges gagnantes de l’AFL 2010 est de 37,75. Bien que l’écart soit évident à interpréter, il est un peu moins évident d’interpréter l’IQR. La façon la plus simple de la penser est la suivante : l’intervalle interquartile est l’intervalle couvert par la « moitié centrale » des données.
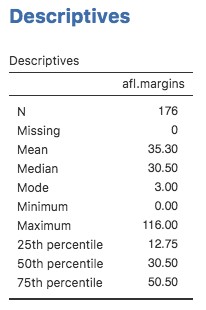
Figure 4‑8 : Une capture d’écran de Jamovi montrant les quartiles de la variable afl. Margins
Autrement dit, un quart des données se situent sous le 25e percentile et un quart des données se situent au-dessus du 75e percentile, laissant la « moitié médiane » des données entre les deux. Et l’IQR est la plage couverte par cette moitié médiane.
4.2.3 Écart moyen absolu
Les deux mesures que nous avons examinées jusqu’ici, l’intervalle et l’intervalle interquartile, reposent toutes deux sur l’idée que nous pouvons mesurer la dispersion des données en examinant les percentiles des données. Cependant, ce n’est pas la seule façon de penser le problème. Une autre approche consiste à sélectionner un point de référence significatif (habituellement la moyenne ou la médiane), puis à signaler les écarts « types » par rapport à ce point de référence. Qu’entend-on par écart « typique » ? Habituellement, il s’agit de la valeur moyenne ou médiane de ces écarts. Dans la pratique, cela conduit à deux mesures différentes : « l’écart absolu moyen » (par rapport à la moyenne) et « l’écart absolu médian » (par rapport à la médiane). D’après ce que j’ai lu, la mesure fondée sur la médiane semble être utilisée dans les statistiques et semble être la meilleure des deux. Mais pour être honnête, je ne pense pas l’avoir vu beaucoup utilisé en psychologie. La mesure basée sur la moyenne apparaît cependant parfois en psychologie. Dans cette section, je parlerai de la première, et je reviendrai sur la deuxième plus tard.
Puisque le paragraphe précédent peut sembler un peu abstrait, examinons un peu plus posément l’écart absolu moyen par rapport à la moyenne. Ce qui est utile à propos de cette mesure est que le nom vous dit exactement comment la calculer. Pensons à nos données de marges gagnantes AFL, et une fois de plus, nous allons commencer par prétendre qu’il n’y a que 5 données au total, avec des marges gagnantes de 56, 31, 56, 8 et 32. Puisque nos calculs reposent sur un examen de l’écart par rapport à un point de référence (dans ce cas la moyenne), la première chose que nous devons calculer est la moyenne, \(\bar{X}\). Pour ces cinq observations, notre moyenne est \(\bar{X}=36.6\). L’étape suivante consiste à convertir chacune de nos observations \(X_{i}\) en un score de déviation. Pour ce faire, nous calculons la différence entre l’observation \(X_{i}\) et la moyenne \(\bar{X}\). C’est-à-dire que le score d’écart est défini comme étant \(X_{i}-\bar{X}\). Pour la première observation de notre échantillon, cela correspond à 56 - 36.6 = 19.4. Bien, c’est assez simple. L’étape suivante du processus consiste à convertir ces écarts en écarts absolus, et nous le faisons en convertissant toute valeur négative en valeur positive. Mathématiquement, nous désignerions la valeur absolue de -3 comme |- 3|, et donc nous disons que |- 3|= 3. Nous utilisons la valeur absolue ici parce que nous ne nous soucions pas vraiment de savoir si la valeur est supérieure à la moyenne ou inférieure à la moyenne, nous voulons simplement savoir si elle est proche de la moyenne. Pour rendre ce processus aussi évident que possible, le tableau ci-dessous montre ces calculs pour les cinq observations :
| En français | quel jeu | valeur | écart à la moyenne | écart absolu |
|---|---|---|---|---|
| Notation | i | \(X_{i}\) | \(X_{i}-\bar{X}\) | \(\left |X_{i}-\bar{X} \right |\) |
| 1 | 56 | 19,4 | 19,4 | |
| 2 | 31 | -5,6 | 5,6 | |
| 3 | 56 | 19,4 | 19,4 | |
| 4 | 8 | -28,6 | 28,6 | |
| 5 | 32 | -4,6 | 4,6 |
Maintenant que nous avons calculé le score d’écart absolu pour chaque observation sur l’ensemble de données, tout ce que nous avons à faire pour calculer la moyenne de ces scores. C’est ce qu’on va faire :
\[ \frac{19,4 + 5,6 + 19,4 + 28,6 + 4,6}{5} = 15,52 \]
Et c’est fini. L’écart absolu moyen pour ces cinq notes est de 15,52.
Cependant, bien que nos calculs pour ce petit exemple soient terminés, il nous reste quelques points à aborder. D’abord, nous devrions vraiment essayer d’écrire une formule mathématique appropriée. Mais pour ce faire, j’ai besoin d’une notation mathématique pour me référer à l’écart absolu moyen. Irritant, « écart moyen absolu » et « écart médian absolu » ont le même acronyme (en anglais MAD), ce qui conduit à un source d’ambiguïté, donc j’ai ferais mieux de trouver quelque chose de différent pour l’écart moyen absolu. Soupir. Ce que je vais faire, c’est d’utiliser AAD à la place, abréviation anglaise de déviation absolue moyenne (average absolute deviation). Maintenant que nous avons une notation non ambiguë, voici la formule qui formalise ce que nous venons de calculer :
\[ \text{AAD}\left( X \right) = \frac{1}{N}\sum_{i = 1}^{N}\left| X_{i} - \bar{X} \right| \]
4.2.4 Variance
Bien que la mesure de l’écart absolu moyen ait son utilité, ce n’est pas la meilleure mesure de la variabilité à utiliser. D’un point de vue purement mathématique, il y a de bonnes raisons de préférer les écarts au carré aux écarts absolus. Si nous faisons cela, nous obtenons une mesure appelée variance, qui a très bonnes propriétés statistiques que je vais ignorer,23 et un énorme défaut psychologique dont je vais faire toute une histoire dans un instant. La variance d’un ensemble de données X est parfois écrite \(Var(X)\), mais elle est plus communément appelée \(s^{2}\) (la raison en sera bientôt plus claire). La formule que nous utilisons pour calculer la variance d’un ensemble d’observations est la suivante :
\[ \text{Var}\left( X \right) = \frac{1}{N}\sum_{i = 1}^{N}{(X_{i} - \bar{X})}^{2} \]
Comme vous pouvez le voir, c’est essentiellement la même formule que celle que nous avons utilisée pour calculer l’écart absolu moyen, sauf qu’au lieu d’utiliser « écarts absolus », nous utilisons « écarts carrés ». C’est pour cette raison que la variance est parfois appelée « écart quadratique moyen ».
Maintenant que nous avons l’idée de base, voyons un exemple concret. Encore une fois, utilisons les cinq premiers résultats de l’AFL comme données. Si nous suivons la même approche que la dernière fois, nous obtenons le tableau suivant :
| En français | quel jeu | valeur | écart à la moyenne | écart au carré |
|---|---|---|---|---|
| Maths | i | \(X_{i}\) | \(X_{i} - \bar{X}\) | \(\left (X_{i}-\bar{X}\right )^{2}\) |
| 1 | 56 | 19,4 | 376,36 | |
| 2 | 31 | -5,6 | 31,36 | |
| 3 | 56 | 19,4 | 376,36 | |
| 4 | 8 | -28,6 | 817,96 | |
| 5 | 32 | -4,6 | 21,16 |
Cette dernière colonne contient tous nos écarts quadratiques, il ne nous reste plus qu’à faire la moyenne. Si nous faisons cela à la main, c’est-à-dire à l’aide d’une calculatrice, nous obtenons une variance de 324,64. Passionnant, n’est-ce pas ? Pour le moment, ignorons la question brûlante que vous vous posez probablement tous (c’est-à-dire ce que signifie une variance de 324,64) et parlons plutôt un peu plus de la façon de faire les calculs dans Jamovi, car cela mettra en évidence quelque chose de très bizarre. Démarrez une nouvelle session Jamovi en cliquant sur le bouton du menu principal (trois lignes horizontales dans le coin supérieur gauche et en sélectionnant « Nouveau ». Saisissez maintenant les cinq premières valeurs de l’ensemble de données des marges afl. dans la colonne A (56, 31, 56, 8, 32). Changez le type de variable en « Continu » et sous « Descriptives » cliquez sur la case à cocher « Variance », vous obtenez les mêmes valeurs de variance que celles que nous avons calculées à la main (324,64). Non, attendez, vous obtenez une réponse complètement différente (405,80) - voir Figure 4‑9. C’est bizarre. Jamovi est bogué ? C’est une faute de frappe ? Suis-je un idiot ?
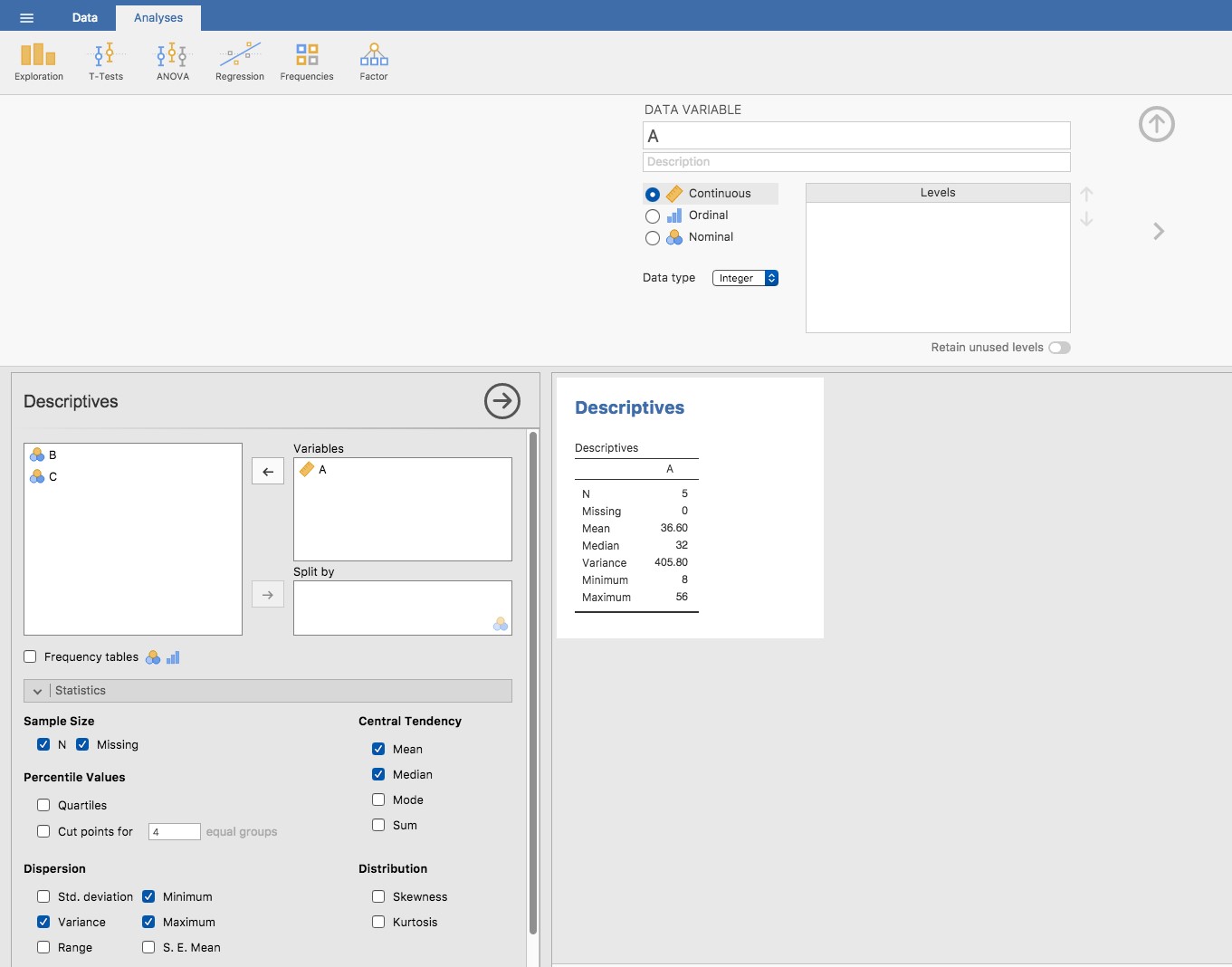
Figure 4‑9 : Une capture d’écran de Jamovi montrant la variance pour les 5 premières valeurs de la variable marges afl.
Il se trouve que la réponse est non.24 Ce n’est pas une faute de frappe, et Jamovi ne fait pas d’erreur. En fait, il est très simple d’expliquer ce que Jamovi fait ici, mais un peu plus difficile d’expliquer pourquoi Jamovi le fait. Commençons donc par le « quoi ». Ce que fait Jamovi, c’est évaluer une formule légèrement différente de celle que je vous ai montrée ci-dessus. Au lieu de faire la moyenne des écarts au carré, ce qui vous oblige à diviser par le nombre de points de données N, Jamovi a choisi de diviser par N - 1. En d’autres termes, la formule que Jamovi utilise est la suivante :
\[ \frac{1}{N - 1}\sum_{i = 1}^{N}{(X_{i} - \overset{\overline{}}{X})}^{2} \]
Voilà donc le quoi. La vraie question est pourquoi Jamovi divise par N - 1 et non par N. Après tout, la variance est supposée être l’écart quadratique moyen, non ? Ne devrions-nous donc pas diviser par N, le nombre réel d’observations dans l’échantillon ? Eh bien, oui, on devrait. Cependant, comme nous le verrons au chapitre 8, il existe une distinction subtile entre « décrire un échantillon » et « faire des suppositions sur la population d’où provient l’échantillon ». Jusqu’à présent, c’était une distinction sans différence. Que vous décriviez un échantillon ou que vous tiriez des conclusions sur la population, la moyenne est calculée exactement de la même façon. Ce n’est pas le cas pour la variance, ni pour l’écart-type, ni pour de nombreuses autres mesures. Ce que je vous ai décrit au départ (c.-à-d. prendre la moyenne réelle, et donc diviser par N) suppose que vous avez littéralement l’intention de calculer la variance de l’échantillon. La plupart du temps, cependant, vous n’êtes pas très intéressé par l’échantillon en soi. L’échantillon existe plutôt pour vous dire quelque chose sur le monde. Si c’est le cas, vous commencez en fait à vous éloigner du calcul d’une « statistique d’échantillon » pour vous diriger vers l’idée d’estimer un « paramètre de population ». Cependant, je m’avance un peu. Pour l’instant, prenons pour acquis que Jamovi sait ce qu’il fait, et nous reviendrons sur cette question plus tard lorsque nous parlerons d’estimation au chapitre 8.
Bien, une dernière chose. Jusqu’à présent, cette section s’est lue un peu comme un roman policier. Je vous ai montré comment calculer la variance, décrit la chose étrange « N – 1 » que fait Jamovi et fait allusion à la raison pour laquelle il le fait, mais je n’ai pas mentionné la chose la plus importante. Comment interprétez-vous la variance ? Les statistiques descriptives sont censées décrire les choses, après tout, et pour le moment, la variance n’est qu’un chiffre en charabia. Malheureusement, la raison pour laquelle je ne vous ai pas donné l’interprétation humaine de la variance est qu’il n’y en a pas vraiment. C’est le problème le plus grave de la variance. Bien qu’il possède d’élégantes propriétés mathématiques qui suggèrent qu’il s’agit vraiment d’une quantité fondamentale pour exprimer la variation, il est complètement inutile si vous voulez communiquer avec un humain réel. Les écarts sont totalement ininterprétables par rapport à la variable d’origine ! Tous les chiffres ont été mis au carré et ils ne veulent plus rien dire. C’est un énorme problème. Par exemple, dans le tableau que j’ai présenté tout à l’heure, la marge dans le jeu 1 était « 376,36 points - plus élevée au carré que la marge moyenne ». C’est exactement aussi stupide que ça en a l’air, et lorsque nous calculons une variance de 324,64, nous sommes dans la même situation. J’ai regardé beaucoup de matchs de foot, et à aucun moment personne n’a jamais fait référence à des « points carrés ». Ce n’est pas une véritable unité de mesure, et puisque la variance est exprimée en termes de cette unité en charabia, elle est totalement dénuée de sens pour un humain.
4.2.5 Écart-type
Supposons que vous aimiez l’idée d’utiliser la variance à cause de ces belles propriétés mathématiques dont je n’ai pas parlé, mais comme vous êtes un humain et non un robot, vous aimeriez avoir une mesure qui est exprimée dans les mêmes unités que les données elles-mêmes (c’est-à-dire des points et non des points carrés). Que devriez-vous faire ? La solution au problème est évidente ! Prenons la racine carrée de la variance, connue sous le nom d’écart-type, également appelée «Racine de l’écart quadratique moyen », ou REQM25. Cela résout notre problème de façon assez nette. Alors que personne n’a pas la moindre idée de ce que signifie réellement « une variance de 324,68 points », il est beaucoup plus facile de comprendre « un écart-type de 18,01 points » puisqu’il est exprimé dans les unités originales. Il est traditionnel de désigner l’écart-type d’un échantillon de données par s, bien que « sd » et « std dev » soient également utilisés à l’occasion.
Comme l’écart-type est égal à la racine carrée de la variance, vous ne serez probablement pas surpris de voir que la formule est :
\[ s = \sqrt{\frac{1}{N}\sum_{i = 1}^{N}{(X_{i} - \overset{\overline{}}{X})}^{2}} \]
et dans Jamovi il y a une case à cocher pour « Standard deviation » juste au-dessus de la case à cocher pour la « Variance ». En sélectionnant cette option, on obtient une valeur de 26,07 pour l’écart-type.
Cependant, comme vous l’avez peut-être noté dans notre discussion sur la variance, ce que Jamovi calcule réellement est légèrement différent de la formule donnée ci-dessus. Tout comme nous l’avons vu avec la variance, ce que Jamovi calcule est une version qui se divise par N - 1 plutôt que N.
Pour des raisons qui auront un sens lorsque nous reviendrons sur ce sujet au chapitre 8, je me référerai à cette nouvelle quantité comme \(\hat{\sigma}\) (lire : « sigma chapeau »), et la formule pour cela est :
\[ \hat{\sigma} = \sqrt{\frac{1}{N - 1}\sum_{i = 1}^{N}{(X_{i} - \overset{\overline{}}{X})}^{2}} \] L’interprétation des écarts-types est légèrement plus complexe. Puisque l’écart-type est dérivé de la variance, et que la variance est une quantité qui a peu ou pas de sens pour nous les humains, l’écart-type n’a pas une interprétation simple. Par conséquent, la plupart d’entre nous ne se fient qu’à une simple règle empirique. En général, vous devriez vous attendre à ce que 68 % des données se situent à l’intérieur d’un écart-type de la moyenne, 95 % des données se situent à l’intérieur de deux écarts-types de la moyenne et 99,7 % des données se situent à l’intérieur de trois écarts-types de la moyenne. Cette règle a tendance à bien fonctionner la plupart du temps, mais elle n’est pas exacte. Il est en fait calculé en supposant que l’histogramme est symétrique et « en forme de cloche ».26 Comme vous pouvez le voir en regardant l’histogramme des marges gagnantes AFL de la Figure 4‑2, ce n’est pas vrai pour nos données ! Malgré cela, la règle est à peu près correcte. Il s’avère que 65,3 % des données sur les marges AFL se situent à l’intérieur d’un écart-type de la moyenne. Ceci est illustré visuellement à la Figure 4‑10.
4.2.6 Quelle mesure utiliser ?
Nous avons discuté d’un certain nombre de mesures de l’écart : la fourchette, l’IQR, l’écart moyen absolu, la variance et l’écart type ; et nous avons fait allusion à leurs forces et à leurs faiblesses. En voici un bref résumé :
Etendue. Vous donne la pleine expansion des données. Elle est très vulnérable aux valeurs aberrantes et en conséquence n’est pas souvent utilisée à moins d’avoir de bonnes raisons de vous soucier des valeurs extrêmes dans les données.
Écart interquartile (IQR). Indique où se trouve la « moitié centrale » des données. Il est assez robuste et complet bien la médiane. On s’en sert beaucoup.
Déviation moyenne absolue. Indique la distance « en moyenne » entre les observations et la moyenne. Il est très interprétable, mais comporte quelques problèmes mineurs (qui ne sont pas abordés ici) qui le rendent moins attrayant pour les statisticiens que l’écart-type. Utilisé parfois,mais pas souvent.
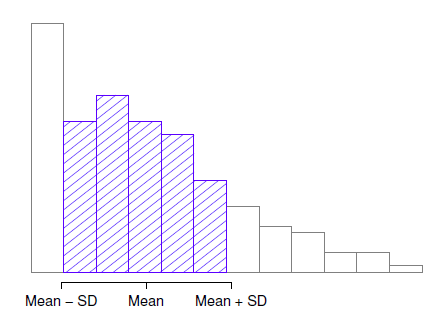
Figure 4‑10 : Illustration de l’écart-type à partir des données des marges gagnantes de l’AFL. Les barres ombragées de l’histogramme indiquent la proportion des données qui se situe à l’intérieur d’un écart-type de la moyenne. Dans ce cas, 65,3 % de l’ensemble des données se situent dans cette fourchette, ce qui est assez conforme à la « règle d’environ 68 % « dont il est question dans le texte principal.
Variance. Vous indique l’écart quadratique moyen par rapport à la moyenne. C’est mathématiquement élégant et c’est probablement la « bonne » façon de décrire la variation autour de la moyenne, mais c’est complètement ininterprétable parce qu’il n’utilise pas les mêmes unités que les données. Presque jamais utilisé sauf comme un outil mathématique, mais il est enfoui « sous le capot » d’un très grand nombre d’outils statistiques.
Écart-type. Il s’agit de la racine carrée de la variance. C’est assez élégant mathématiquement et c’est exprimé dans les mêmes unités que les données, de sorte qu’on peut assez bien l’interpréter. Dans les situations où la moyenne est la mesure de la tendance centrale, c’est la valeur par défaut. C’est de loin la mesure de variation la plus populaire.
En résumé, l’IQR et l’écart-type sont aisément les deux mesures les plus couramment utilisées pour rendre compte de la variabilité des données. Mais il y a des situations où les autres sont utilisées. Je les ai tous décrits dans ce livre parce qu’il y a de fortes chances que vous en rencontriez la plupart quelque part.
4.3 Asymétrie et aplatissement
Il y a deux autres statistiques descriptives que vous verrez parfois rapportées dans la littérature psychologique : l’asymétrie (skew) et l’aplatissement (kurtosis). Dans la pratique, ni l’une ni l’autre n’est utilisée aussi fréquemment que les mesures de la tendance centrale et de la variabilité dont nous avons parlé. L’asymétrie est assez importante, donc vous verrez qu’il en est fait mention assez souvent, mais je n’ai jamais vu d’applatissement rapporté dans un article scientifique à ce jour.
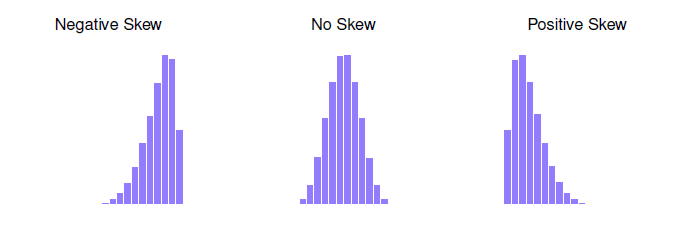
Figure 4‑11 : Une illustration de l’asymétrie (skew). Sur la gauche nous avons un ensemble de données négatives (skewness = -.93), au milieu nous avons un ensemble de données sans asymétrie (enfin, presque pas : skewness =.-.006), et sur la droite nous avons un ensemble de données positivement asymétriques (skewness = .93).
Puisque c’est le plus intéressant des deux, commençons par parler de l’asymétrie. L’asymétrie est fondamentalement une mesure de l’asymétrie et la façon la plus facile de l’expliquer est de dessiner quelques images. Comme l’illustre la Figure 4‑11, si les données ont tendance à avoir beaucoup de valeurs extrêmement petites (c.-à-d. que la queue inférieure est « plus longue « que la queue supérieure) et pas autant de valeurs extrêmement grandes (panneau de gauche), nous disons que les données sont faussées de façon négative. Par contre, s’il y a des valeurs plus importantes que des valeurs extrêmement faibles (panneau de droite), nous disons que les données sont positivement faussées. C’est l’idée qualitative derrière l’asymétrie. S’il y a relativement plus de valeurs qui sont beaucoup plus grandes que la moyenne, la distribution est positivement inclinée ou inclinée vers la droite, avec une queue qui s’étend vers la droite. Le biais négatif ou gauche est le contraire. Une distribution symétrique a une asymétrie de 0, la valeur d’asymétrie pour une distribution positivement asymétrique est positive, et une valeur négative pour une distribution négativement asymétrique.
Une formule pour l’asymétrie d’un ensemble de données est la suivante
\[ \text{skewness}\left( X \right) = \frac{1}{N{\hat{\sigma}}^{3}}\sum_{i = 1}^{N}{(X_{i} - \overset{\overline{}}{X})}^{3} \]
où N est le nombre d’observations, \(\overset{\overline{}}{X}\) est la moyenne de l’échantillon et \(\hat{\sigma}\) est l’écart-type (la version « divisé par N – 1 »).
Peut-être pour vous aider, vous pourriez utiliser Jamovi pour calculer l’asymétrie : c’est une case à cocher dans les options « Statistiques » sous « Exploration » - « Descriptifs ». Pour la variable afl.margins, l’asymétrie est de 0,780. Si vous divisez l’estimation de l’asymétrie par l’erreur standard d’asymétrie, vous obtenez une indication de l’asymétrie des données. Surtout dans les petits échantillons (N<50), une règle empirique suggère qu’une valeur de 2 ou moins peut signifier que les données ne sont pas très asymétriques, et une valeur de plus de 2 qu’il y a suffisamment de biais dans les données pour éventuellement limiter leur utilisation dans certaines analyses statistiques. Il n’y a cependant pas d’accord clair sur cette interprétation. Malgré tout cela indique que les données sur les marges gagnantes de l’AFL sont quelque peu asymétriques (0,780 / 0,183 = 4,262).
La dernière mesure à laquelle on se réfère parfois, mais très rarement dans la pratique, est l’aplatissement d’un ensemble de données. En termes simples, l’aplatissement est une mesure de « l’acuité » d’un ensemble de données, comme l’illustre la Figure 4‑12. Par convention, on dit que la « courbe normale » (lignes noires) a une kurtosis nulle, de sorte que le point d’un ensemble de données est évalué par rapport à cette courbe.
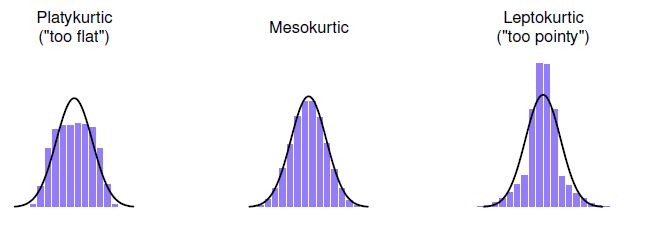
Figure 4‑12 : Une illustration de l’aplatissement. A gauche, nous avons un ensemble de données « platykurtique » (kurtosis = -.95) qui signifie que l’ensemble de données est « trop plat ». Au milieu, nous avons un ensemble de données « mésokurtiques » (kurtosis est presque égal à 0), ce qui signifie que la précision des données est à peu près correcte. Enfin, à droite, nous avons un ensemble de données « leptokurtiques » (kurtosis = 2.12) indiquant que l’ensemble de données est « trop pointu ». Notez que l’aplatissement est mesuré par rapport à une courbe normale (ligne noire).
Dans cette figure, les données à gauche ne sont pas assez pointues, donc le kurtosis est négatif et nous appelons les données platykurtiques. Les données à droite sont trop pointues, donc l’aplatissement est positif et nous disons que les données sont leptokurtiques. Mais les données au milieu sont juste assez pointues, donc nous disons qu’il est mésokurtique et a un kurtosis égal à zéro. Ce point est résumé dans le tableau ci-dessous :
| Terme informel | Nom technique | Valeur du kurtosis |
|---|---|---|
| trop plat | platykurtique | négatif |
| Juste assez pointu | mésokurtique | zero |
| trop pointu | leptokurtique | positif |
L’équation de l’aplatissement est assez semblable de conception aux formules que nous avons déjà vues pour la variance et l’asymétrie. Sauf que lorsque la variance impliquait des écarts au carré et que l’asymétrie impliquait des écarts au cube, l’aplatissement impliquait d’augmenter les écarts à la puissance quatre27 :
\[ \text{kurtosis}\left( X \right) = \frac{1}{N{\hat{\sigma}}^{4}}\sum_{i = 1}^{N}{{(X_{i} - \overset{\overline{}}{X})}^{4} - 3} \]
Je sais, ce n’est pas très intéressant pour moi non plus.
Plus précisément, Jamovi a une case à cocher pour l’aplatissement juste en dessous de la case à cocher pour l’asymétrie, ce qui donne une valeur pour l’aplatissement de 0,101 avec une erreur standard de 0,364. Cela signifie que les données de marges gagnantes AFL sont juste assez pointues.
4.4 Statistiques descriptives distinctes pour chaque groupe
Il est très fréquent que vous ayez besoin d’examiner des statistiques descriptives ventilées par variable de regroupement. C’est assez facile à faire avec Jamovi. Par exemple, supposons que je veux examiner les statistiques descriptives de certaines données de clin.trial, ventilées séparément par type de thérapie. Il s’agit d’un nouvel ensemble de données que vous n’avez jamais vu auparavant. Les données sont stockées dans le fichier clinicaltrial.csv et nous les utiliserons beaucoup au chapitre 13 (vous trouverez une description complète des données au début de ce chapitre). Chargeons-le et voyons ce qu’on a :
Évidemment, il y avait trois médicaments : un placebo, quelque chose appelé « anxifree » et quelque chose appelé « joyzepam », et il y avait 6 personnes qui recevaient chaque médicament. Neuf personnes ont été traitées par thérapie cognitivo-comportementale (TCC) et neuf personnes n’ont reçu aucun traitement psychologique. Et nous pouvons voir en regardant les « Descriptives » de la variable mood.gain que la plupart des gens ont montré un gain d’humeur (moyenne = 0.88), bien que sans savoir quelle est l’échelle ici, il est difficile d’en dire beaucoup plus que cela. Mais ce n’est pas si mal. Dans l’ensemble, j’ai l’impression d’avoir appris quelque chose avec cela.
Nous pouvons également examiner d’autres statistiques descriptives, et cette fois-ci séparément pour chaque type de thérapie. Dans Jamovi, cochez « Std deviation », « Skewness » et « Kurtosis » dans les options « Statistics ». En même temps, faite glisser la variable de therapy dans la case « Split by »28, et vous devriez obtenir quelque chose comme Figure 4‑14
Figure 4‑13 : Une capture d’écran de Jamovi montrant les variables stockées dans le fichier clinicaltrial.csv
Qu’arrive-t-il si vous avez plusieurs variables de regroupement ? Supposons que vous souhaitiez examiner séparément le gain moyen de l’humeur pour toutes les combinaisons possibles de médicaments et de traitements. Il est possible de le faire en ajoutant une autre variable, le médicament (Drug), dans la case « Split by ». Facile, bien que parfois, si vous divisez trop, il n’y a pas assez de données dans chaque combinaison de décomposition pour faire des calculs significatifs. Dans ce cas, Jamovi vous le dit en disant quelque chose comme NaN ou Inf.29
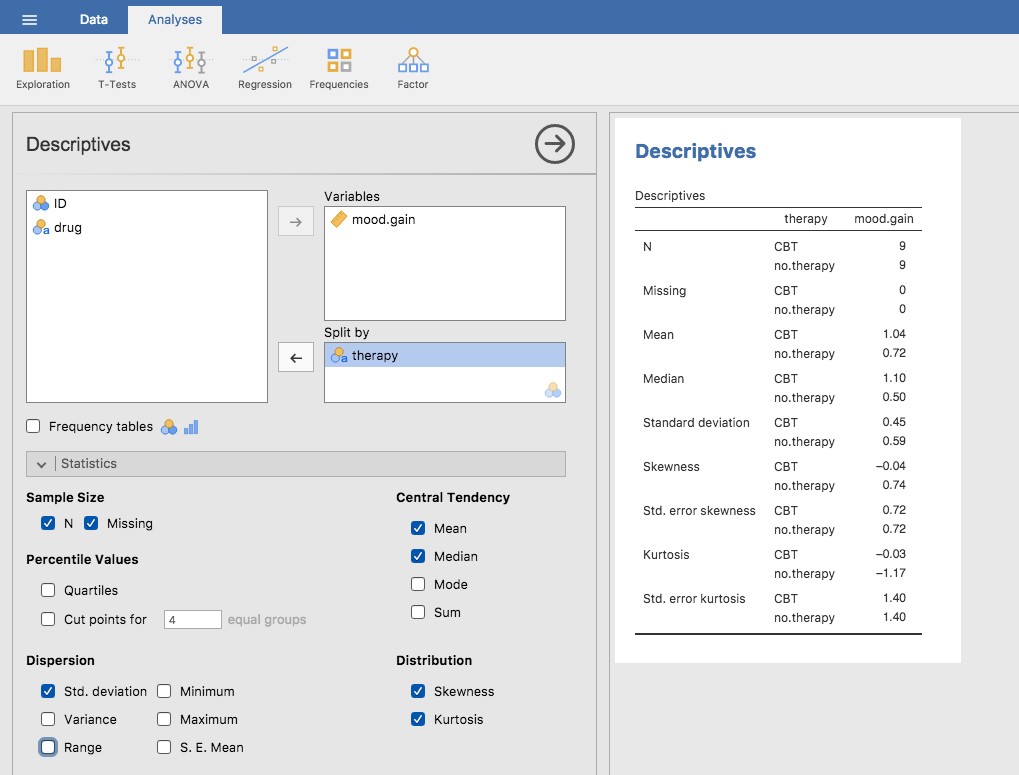
Figure 4‑14 : Une capture d’écran de Jamovi montrant les descriptions par type de thérapie
4.5 Scores standards
Supposons que mon ami est en train de mettre au point un nouveau questionnaire destiné à mesurer le « grincheux ». L’enquête comporte 50 questions auxquelles vous pouvez répondre de façon grincheuse ou non. Sur un grand échantillon (hypothétiquement, imaginons un million de personnes environ !), les données sont distribuées assez normalement, le score moyen de grincheux étant de 17 sur 50 questions auxquelles on répond de façon grincheuse, et l’écart-type étant de 5. En revanche, lorsque je réponds au questionnaire, je le fais d’une façon grincheuse à 35 questions sur 50. Alors, à quel point suis-je grincheux ? Une façon de le voir serait de dire que j’ai une grinchiosité de 35/50, donc on pourrait dire que je suis grincheux à 70%. Mais c’est un peu bizarre, quand on y pense. Si mon amie avait formulé ses questions un peu différemment, les gens auraient pu y répondre d’une manière différente, de sorte que la distribution globale des réponses pourrait facilement monter ou descendre en fonction de la façon précise dont les questions ont été posées. Donc, je ne suis grincheux à 70 p. 100 qu’en ce qui concerne cet ensemble de questions du sondage. Même s’il s’agit d’un très bon questionnaire, ce n’est pas une déclaration très informative.
Une façon plus simple de contourner ce problème est de décrire ma grinchiosité en me comparant à d’autres personnes.
Étonnamment, sur l’échantillon de 1 000 000 de personnes de mon ami, seulement 159 étaient aussi grincheux que… moi (ce n’est pas du tout irréaliste, franchement) suggérant que je suis dans le top 0,016% des grincheux. Cela a beaucoup plus de sens que d’essayer d’interpréter les données brutes. Cette idée selon laquelle nous devrions décrire ma grinchiosité en termes de distribution globale de la grinchiosité des humains, est l’idée qualitative à laquelle la normalisation tente d’aboutir. Une façon d’y parvenir est de faire exactement ce que je viens de faire et de tout décrire en termes de percentiles. Cependant, le problème en faisant ça, c’est qu’on se sent seul au sommet. Supposons que mon ami n’ait collecté qu’un échantillon de 1000 personnes (j’aimerais ajouter encore que c’est un échantillon assez important pour tester un nouveau questionnaire) et cette fois-ci, nous ayons obtenu, disons, une moyenne de 16 sur 50 avec un écart-type de 5. Le problème, c’est qu’il est presque certain qu’aucune personne de cet échantillon ne serait aussi grincheuse… que moi. Cependant, tout n’est pas perdu. Une approche différente consiste à convertir mon score grincheux en un score standard, également appelé score z. Le score standard est défini comme le nombre d’écarts-types au-dessus de la moyenne de mon score de grinchiosité. Pour l’exprimer en « pseudo-maths », on calcule le score standard de la manière suivante :
\[ \text{Score}\ \text{standard} = \frac{\text{Score}\ \text{observ}e - \text{moyenne}}{e\text{cart} - \text{type}} \]
En mathématiques réelles, l’équation pour le z-score est la suivante
\[ z_{i} = \frac{X_{i}\_\overset{\overline{}}{X}}{\hat{\sigma}} \]
Donc, pour en revenir aux données sur la grinchiosité, nous pouvons maintenant transformer la grinchiosité brute de Dani en un score de grinchiosité standardisé.
\[ z = \frac{35 - 17}{5}3,6 \]
Pour interpréter cette valeur, rappelez-vous l’heuristique grossière que j’ai fournie à la section 4.2.5 dans laquelle j’ai noté que 99,7 % des valeurs devraient se situer dans les 3 écarts-types de la moyenne. Le fait que ma grinchiosité correspond à un score z de 3,6 indique que je suis très grincheux en effet. En fait, cela suggère que je suis plus grincheux que 99,98% des gens. C’est à peu près ça.
En plus de vous permettre d’interpréter un score brut par rapport à une population plus large (et donc de donner un sens à des variables qui reposent sur des échelles arbitraires), les scores standard ont une deuxième fonction utile. Les scores standards peuvent être comparés les uns aux autres dans des situations où les scores bruts ne le peuvent pas. Supposons, par exemple, que mon ami avait aussi un autre questionnaire qui mesurait l’extraversion à l’aide d’un questionnaire à 24 items. Comme vous pouvez l’imaginer, cela n’a pas beaucoup de sens d’essayer de comparer mon score brut de 2 sur le questionnaire d’extraversion à mon score brut de 35 sur le questionnaire de grincheux. Les scores bruts pour les deux variables sont « à peu près » fondamentalement différents, donc ce serait comme comparer des pommes à des oranges.
Qu’en est-il des scores standards ? Eh bien, c’est un peu différent. Si nous calculons les scores standards, nous obtenons z = (35-17)/5 = 3,6 pour la grinchiosité et z = (2-13)/4 = 2,75 pour l’extraversion.
Ces deux nombres peuvent être comparés l’un à l’autre.30 Je suis beaucoup moins extraverti que la plupart des gens (z = -2,75) et beaucoup plus grincheux que la plupart des gens (z = 3.6). Mais l’ampleur de mon étrangeté est beaucoup plus extrême pour la grinchiosité, puisque 3,6 est un chiffre supérieur à 2,75. Parce que chaque score standardisé est une indication de la position d’une observation par rapport à sa propre population, il est possible de comparer des scores standardisés pour des variables complètement différentes.
4.6 Résumé
Calculer quelques statistiques descriptives de base est l’une des toutes premières choses que vous faites lorsque vous analysez des données réelles, et les statistiques descriptives sont beaucoup plus simples à comprendre que les statistiques inférentielles, donc comme dans tous les autres manuels de statistiques, j’ai commencé avec des statistiques descriptives. Dans ce chapitre, nous avons abordé les sujets suivants :
- Mesures de tendance centrale. D’une manière générale, les mesures de tendance centrale vous indiquent où se trouvent les données. Trois mesures sont habituellement mentionnées dans la documentation : la moyenne, la médiane et le mode. (Section 4.1)
- Mesures de la variabilité. Par contre, les mesures de variabilité vous renseignent sur la façon dont les données sont « étalées «. Les principales mesures sont : l’intervalle, l’écart-type et l’intervalle interquartile.(Section 4.2)
- Mesures de l’asymétrie et de l’aplatissement. Nous avons également étudié l’asymétrie dans la distribution d’une variable (skew) et l’applatissement (kurtosis). (Section 4.3)
- Obtenir des résumés de groupes de variables dans Jamovi. Puisque ce livre se concentre sur l’analyse des données dans Jamovi, nous avons passé un peu de temps à parler de la façon dont les statistiques descriptives sont calculées pour différents sous-groupes. (Section 4.4)
- Score standard. Le z-score est une bête un peu inhabituelle. Ce n’est pas tout à fait une statistique descriptive, ni une inférence. Nous en avons parlé à la section 4.5. Assurez-vous de bien comprendre cette section. On en reparlera plus tard.
Dans le prochain chapitre, nous passerons à une discussion sur la façon de dessiner des images ! Tout le monde aime les belles photos, non ? Mais avant de le faire, je voudrais terminer sur un point important. Un premier cours traditionnel en statistique ne consacre qu’une petite partie de la classe à la statistique descriptive, peut-être une ou deux conférences tout au plus. La grande majorité du temps du conférencier est consacrée aux statistiques inférentielles parce que c’est là que se trouvent toutes les choses difficiles. C’est logique, mais cela cache l’importance pratique quotidienne de choisir de bonnes descriptions. Avec cela à l’esprit….
4.6.1 Epilogue : Les bonnes statistiques descriptives sont descriptives !
La mort d’un homme est une tragédie. La mort de millions de personnes est une statistique. - Josef Staline, Potsdam 1945
950 000 – 1 200 000 - Estimation du nombre de victimes de la répression soviétique, 1937-1938 (Ellman 2002)
La citation tristement célèbre de Staline sur le caractère statistique de la mort de millions de personnes mérite réflexion. L’intention claire de sa déclaration est que la mort d’un individu nous touche personnellement et sa force ne peut être niée, mais que les morts d’une multitude sont incompréhensibles et, par conséquent, sont de simples statistiques plus facilement ignorées. Je dirais que Staline avait à moitié raison. Une statistique est une abstraction, une description d’événements au-delà de notre expérience personnelle, et si difficile à visualiser. Peu d’entre nous, sinon aucun d’entre nous, ne peut imaginer à quoi ressemble « vraiment » la mort de millions de personnes, mais nous pouvons imaginer une seule mort et cela donne à la seule mort son sentiment de tragédie immédiate, un sentiment qui manque dans la description statistique froide d’Ellman.
Pourtant, ce n’est pas si simple. Sans chiffres, sans dénombrement, sans description de ce qui s’est passé, nous n’avons aucune chance de comprendre ce qui s’est réellement passé, aucune occasion même d’essayer d’invoquer le sentiment manquant. Et en vérité, au moment où j’écris ces lignes, assis confortablement un samedi matin, à la moitié d’une vie et loin des goulags, lorsque je mets l’estimation d’Ellman à côté de la citation de Staline, une crainte obsédante me prend l’estomac et un frisson me parcourt.
La répression stalinienne est quelque chose qui dépasse vraiment mon expérience, mais avec une combinaison de données statistiques et d’histoires personnelles enregistrées qui nous sont parvenues, ce n’est pas entièrement au-delà de ma compréhension. Parce que les chiffres d’Ellman nous disent ceci : sur une période de deux ans, la répression stalinienne a anéanti l’équivalent de chaque homme, femme et enfant vivant actuellement dans la ville où je vis. Chacun de ces décès avait sa propre histoire, sa propre tragédie, et nous n’en connaissons que quelques-uns à l’heure actuelle. Malgré tout, avec quelques statistiques soigneusement choisies, l’ampleur de l’atrocité commence à se faire sentir.
Il n’est donc pas anodin de dire que la première tâche du statisticien et du scientifique est de résumer les données, de trouver un ensemble de chiffres qui puissent transmettre à un public une idée de ce qui s’est passé. C’est le travail des statistiques descriptives, mais ce n’est pas un travail qui est fait uniquement à l’aide des chiffres. Vous êtes un analyste de données et non un logiciel statistique. Une partie de votre travail consiste à prendre ces statistiques et à les transformer en une description. Lorsque vous analysez des données, il ne suffit pas d’énumérer une collection de chiffres. Rappelez-vous toujours que ce que vous essayez vraiment de faire, c’est de communiquer avec un public humain. Les chiffres sont importants, mais ils doivent être rassemblés en une histoire significative que votre auditoire peut interpréter. Cela signifie que vous devez penser à la structure. Vous devez penser au contexte. Et vous devez penser aux événements individuels que vos statistiques résument.
References
Ellman, Michael. 2002. “Soviet Repression Statistics: Some Comments.” Europe-Asia Studies 54 (7): 1151–72.
Note pour les non-Australiens : l’AFL est une compétition de football aux règles australiennes. Vous n’avez pas besoin de connaître les règles australiennes pour suivre cette section.↩︎
Le choix d’utiliser \(\sum\) pour indiquer la sommation n’est pas arbitraire. C’est la lettre grecque en majuscules sigma, qui est l’analogue de la lettre S dans cet alphabet. De même, il y a un symbole équivalent utilisé pour désigner la multiplication de beaucoup de nombres, parce que les multiplications sont aussi appelées « produits » nous utilisons le symbole \(\Pi\) pour cela (le grec en majuscule pi, qui est l’analogue de la lettre P).↩︎
Bien, je vais mentionner très brièvement celle que je trouve la plus cool, avec une définition très particulière du mot « cool ». Les variances sont additives. Voici ce que ça veut dire. Supposons que j’ai deux variables X et Y, dont les variances sont respectivement Var(X) et Var(Y). Imaginez maintenant que je veuille définir une nouvelle variable Z qui est la somme des deux, Z = X + Y. Il s’avère que la variance de Z est égale à Var(X) + Var(Y). C’est une propriété très utile et qui n’est pas vraie des autres mesures dont je présente dans cette section.↩︎
À l’exception peut-être de la troisième question.↩︎
NdT. En anglais « root mean squared deviation” ou RMSD↩︎
A strictement parler, l’hypothèse est que les données sont normalement distribuées, ce qui est un concept important dont nous parlerons plus en détail au chapitre 7 et sur lequel nous reviendrons encore et encore plus loin dans le livre.↩︎
La partie « -3 » est quelque chose que les statisticiens collent pour s’assurer que la courbe normale a un kurtosis zéro. Cela semble un peu stupide, il suffit de coller un « -3 » à la fin de la formule, mais il y a de bonnes raisons mathématiques de le faire.↩︎
NdT « Split by » signifie « divisé par »↩︎
Parfois, Jamovi présentera aussi des chiffres d’une manière inhabituelle. Si un nombre est très petit, ou très grand, alors Jamovi passe à une forme exponentielle pour les nombres. Par exemple, 6.51e-4 revient à dire que le point décimal est déplacé de 4 positions vers la gauche, donc le nombre réel est 0.000651. S’il y a un signe plus (c’est-à-dire 6.51e+4), la virgule décimale est déplacée vers la droite, c’est-à-dire 65 100,00. Habituellement, seuls des nombres très petits ou très grands sont exprimés de cette façon, par exemple 6.51e-16, ce qui serait très difficile à écrire de la manière habituelle.↩︎
Bien qu’une certaine prudence soit généralement de mise. Il n’est pas toujours vrai qu’un écart-type sur la variable A correspond au même « type » de chose qu’un écart-type sur la variable B. Faites preuve de bon sens lorsque vous essayez de déterminer si les scores z de deux variables peuvent être comparés de façon significative.↩︎