Chapitre 16 Statistiques bayésiennes

Dans nos raisonnements concernant les faits, il y a tous les degrés d’assurance imaginables, de la plus haute certitude à la plus basse espèce de preuve morale. Un homme sage, par conséquent, proportionne sa croyance à l’évidence. - David Hume¹⁴²

Les idées que je vous ai présentées dans ce livre décrivent les statistiques inférentielles du point de vue des fréquentistes. Je ne suis pas le seul à le faire. En fait, presque tous les manuels scolaires donnés aux étudiants de premier cycle en psychologie présentent le point de vue du statisticien fréquentiste comme la théorie de la statistique inférentielle, la seule véritable façon de faire les choses. J’ai enseigné de cette façon pour des raisons pratiques. La vision fréquentiste de la statistique a dominé le champ académique de la statistique pendant la majeure partie du XXe siècle, et cette domination est encore plus extrême chez les scientifiques appliqués. C’était et c’est une pratique courante chez les psychologues d’utiliser des méthodes fréquentistes. Parce que les méthodes fréquentistes sont omniprésentes dans les articles scientifiques, chaque étudiant en statistique doit comprendre ces méthodes, sinon il sera incapable de comprendre ce que disent ces articles ! Malheureusement, du moins à mon avis, la pratique actuelle de la psychologie est souvent malavisée et le recours aux méthodes fréquentistes est en partie responsable. Dans ce chapitre, j’explique pourquoi je pense cela et je donne une introduction aux statistiques bayésiennes, une approche qui, à mon avis, est généralement supérieure à l’approche orthodoxe.

Ce chapitre est divisé en deux parties. Dans les sections 16.1 à 16.3, j’explique en quoi consistent les statistiques bayésiennes, les règles mathématiques de base de leur fonctionnement ainsi que les raisons pour lesquelles l’approche bayésienne me semble si utile. Par la suite, je donne un bref aperçu de la façon dont vous pouvez faire des versions bayésiennes de t-tests (Section 16.4).

16.1 Raisonnement probabiliste des agents rationnels

D’un point de vue bayésien, l’inférence statistique est une question de révision des croyances. Je pars d’un ensemble d’hypothèses candidates h sur le monde. Je ne sais pas laquelle de ces hypothèses est vraie, mais j’ai des croyances sur les hypothèses qui sont plausibles et celles qui ne le sont pas. Quand j’observe les données, d, je dois réviser ces croyances. Si les données sont cohérentes avec une hypothèse, ma croyance en cette hypothèse est renforcée. Si les données ne concordent pas avec l’hypothèse, ma croyance en cette hypothèse s’en trouve affaiblie. A la fin de cette section, je donnerai une description précise du fonctionnement du raisonnement bayésien, mais je veux d’abord travailler sur un exemple simple pour présenter les idées clés. Considérons le problème de raisonnement suivant.

Je prends un parapluie. Croyez-vous qu’il va pleuvoir ?

Dans ce problème, je vous ai présenté un seul élément de données (d = Je prends le parapluie), et je vous demande de me dire votre croyance ou votre hypothèse sur la pluie. Vous avez deux alternatives, h : soit il pleuvra aujourd’hui, soit il ne pleuvra pas. Comment résoudre ce problème ?

16.1.1 A priori : ce que vous croyiez avant

La première chose que vous devez faire est d’ignorer ce que je vous ai dit au sujet du parapluie, et de noter vos croyances préexistantes sur la pluie. C’est important. Si vous voulez être honnête sur la façon dont vos croyances ont été révisées à la lumière de nouvelles preuves (données) alors vous devez dire quelque chose sur ce que vous croyiez avant que ces données n’apparaissent ! Bien, que pourriez-vous croire à propos du fait qu’il va pleuvoir aujourd’hui ? Vous savez probablement que je vis en Australie et qu’une grande partie de l’Australie est chaude et sèche. La ville d’Adélaïde où je vis a un climat méditerranéen, très similaire à celui de la Californie du Sud, de l’Europe du Sud ou de l’Afrique du Nord. J’écris ceci en janvier et vous pouvez donc supposer que c’est le milieu de l’été. En fait, vous avez peut-être décidé de jeter un coup d’œil sur Wikipédia¹⁴³ et découvert qu’Adélaïde reçoit en moyenne 4,4 jours de pluie pendant les 31 jours de janvier. Sans rien savoir d’autre, vous pourriez conclure que la probabilité de pluie en janvier à Adélaïde est d’environ 15%, et la probabilité d’une journée sèche est de 85%. Si c’est vraiment ce que vous croyez au sujet de la pluie d’Adélaïde (et maintenant que je vous l’ai dit, je parie que c’est vraiment ce que vous croyez) alors ce que j’ai écrit ici est votre distribution à priori, écrite P(h):

hypothesis	Degree of belief
Rainy day	0.15
Dry day	0.85

16.1.2 Probabilités : théories sur les données

Pour résoudre le problème de raisonnement, vous avez besoin d’une théorie sur mon comportement. Quand Dan prend-il un parapluie ? Vous devinerez peut-être que je ne suis pas un idiot¹⁴⁴, et j’essaie de ne prendre des parapluies que les jours de pluie. D’un autre côté, vous savez aussi que j’ai de jeunes enfants, et vous ne seriez pas surpris d’apprendre que j’ai tendance à oublier ce genre de choses. Supposons que les jours de pluie, je me souviens de mon parapluie environ 30% du temps (je suis vraiment nul à ce jeu).

Mais disons que par temps sec, je n’ai que 5% de chances de prendre un parapluie. Vous pourriez écrire une petite table comme celle-ci :

	Data
Hypothesis	Umbrella	No umbrella
Rainy day	0.30	0.70
Dry day	0.05	0.95

Il est important de se rappeler que chaque cellule de ce tableau décrit vos croyances sur les données d qui seront observées, étant donné la véracité d’une hypothèse particulière h. Cette « probabilité conditionnelle » est écrite \(P\left(d\mid h \right)\), que vous pouvez lire comme « la probabilité de d donnée h ». Dans les statistiques bayésiennes, il s’agit de la probabilité des données d compte tenu de l’hypothèse h.¹⁴⁵

16.1.3 La probabilité conjointe des données et des hypothèses

À ce stade, tous les éléments sont en place. Après avoir noté les à priori et la probabilité, vous avez toute l’information dont vous avez besoin pour faire le raisonnement bayésien. La question est maintenant de savoir comment utiliser cette information. Il s’avère qu’il y a une équation très simple que nous pouvons utiliser ici, mais il est important que vous compreniez pourquoi nous l’utilisons, alors je vais essayer de la construire à partir d’idées plus simples.

Commençons par une des règles de la théorie des probabilités. Je l’ai énuméré dans le Tableau 7‑1, mais je n’en ai pas fait grand cas à l’époque et vous l’avez probablement ignoré. La règle en question est celle qui parle de la probabilité que deux choses soient vraies. Dans notre exemple, vous voudrez peut-être calculer la probabilité qu’aujourd’hui soit pluvieux (c’est-à-dire que l’hypothèse h soit vraie) et que je prenne un parapluie (c’est-à-dire que les données d soient observées). La probabilité conjointe de l’hypothèse et des données est écrite P(d,h), et vous pouvez la calculer en multipliant l’à priori P(h) par la probabilité \(P\left(d \mid h\right)\). Mathématiquement, nous disons que

\[ P\left( d,h \right) = P\left( d \middle| h \right)P(h) \]

Alors, quelle est la probabilité qu’aujourd’hui soit un jour de pluie et que je me souvienne de prendre un parapluie ? Comme nous l’avons vu plus haut, l’à priori nous dit que la probabilité d’un jour de pluie est de 15%, et la probabilité que je me souvienne de prendre mon parapluie un jour de pluie est de 30%. Ainsi, la probabilité que ces deux évènements soient vrais est calculée en multipliant les deux valeurs suivantes

\[\begin{aligned} P\left(\text{rainy,umbrella} \right) &= P\left( \text{rainy} \mid \text{umbrella} \right) \times P\left( \text{rainy}\right)\\ &= 0,30 \times 0,15\\ &= 0,045 \end{aligned} \]

En d’autres termes, avant de savoir ce qui s’est réellement passé, vous pensez qu’il y a une probabilité de 4,5% qu’aujourd’hui soit un jour de pluie et que je me souvienne du parapluie. Cependant, il y a bien sûr quatre évènements qui peuvent arriver. Répétons donc l’exercice pour les quatre. Si nous faisons cela, nous obtenons le tableau suivant :

	Umbrella	No umbrella
Rainy	0.0450	0.1050
Dry	0.0425	0.8075

Ce tableau saisit toutes les informations sur les probabilités des des quatre possibilités. Pour avoir une vue d’ensemble, cependant, il est utile d’additionner les totaux des lignes et des colonnes. Cela nous donne cette table :

	Umbrella	No umbrella	Total
Rainy	0.0450	0.1050	0.15
Dry	0.0425	0.8075	0.85
Total	0.0875	0.9125	1

C’est un tableau très utile, il vaut donc la peine de prendre un moment pour réfléchir à ce que tous ces chiffres nous disent. Tout d’abord, notez que les sommes des lignes ne nous disent rien de nouveau du tout. Par exemple, la première rangée nous dit que si nous ignorons toute cette affaire de parapluie, la probabilité qu’aujourd’hui soit un jour de pluie est de 15%. Ce n’est pas surprenant, bien sûr, puisque c’est notre à priori.¹⁴⁶ L’important n’est pas les nombres eux-même. Au contraire, l’important, c’est que cela nous donne une certaine confiance que nos calculs sont raisonnables ! Maintenant, jetez un coup d’oeil aux sommes de la colonne et remarquez qu’elles nous disent quelque chose que nous n’avons pas encore explicitement indiqué. De la même manière que les sommes des lignes nous indiquent la probabilité de pluie, les sommes des colonnes nous indiquent la probabilité que je prenne un parapluie. Plus précisément, la première colonne nous indique qu’en moyenne (c.-à-d. en ignorant si c’est un jour de pluie ou non) la probabilité que je prenne un parapluie est de 8,75 %. Enfin, notons que lorsque nous additionnons les quatre événements logiquement possibles, le total vaut 1, c’est-à-dire que nous avons écrit une distribution de probabilités correcte, définie sur toutes les combinaisons possibles de données et d’hypothèses.

Maintenant et parce que ce tableau est si utile, je veux m’assurer que vous comprenez à quoi correspondent tous les éléments et comment ils sont notés :

	Umbrella	No umbrella
Rainy	P(umbrella, Rainy)	P(No Umbrella, Rainy)	P(Rainy)
Dry	P(umbrella, Dry)	P(No umbrella, Dry)	P(Dry)
	P(umbrella)	P(No umbrella)

Enfin, nous pouvons utiliser une notation statistique « correcte ». Dans le problème des jours de pluie, les données correspondent à l’observation que j’ai ou non un parapluie. Nous allons noter d₁ la possibilité que vous m’observiez en prenant un parapluie, et d₂ à la possibilité que vous m’observiez en n’en prenant pas. De même, h₁ est votre hypothèse qu’aujourd’hui il pleut et h₂ est l’hypothèse que ce n’est pas le cas. En utilisant cette notation, le tableau ressemble à ceci :

	d₁	d₂
h₁	P(h₁,d₁)	P(h₁,d₂)	P(h₁)
h₂	P(h₂,d₁)	P(h₂,d₂)	P(h₂)
	P(d₁)	P(d₂)

16.1.4 Révision des croyances à l’aide de la règle de Bayes

Le tableau que nous avons présenté dans la dernière section est un outil très puissant pour résoudre le problème des jours de pluie, parce qu’il considère les quatre possibilités logiques et indique exactement dans quelle mesure vous avez confiance en chacune d’elles avant de recevoir des données. Il est maintenant temps de réfléchir à ce qu’il adviendra de nos croyances lorsque nous recevrons les données. Dans le problème des jours de pluie, on vous dit que je prends vraiment un parapluie. C’est un événement assez surprenant. Selon notre tableau, la probabilité que je porte un parapluie n’est que de 8,75 %. Mais est-ce logique ? Un type qui prend un parapluie un jour d’été dans une ville chaude et sèche est assez inhabituel, et vous ne vous y attendiez pas du tout. Néanmoins, les données vous disent que c’est vrai. Aussi improbable que vous pensiez que soit, vous devez maintenant ajuster vos croyances pour tenir compte du fait que vous savez maintenant que j’ai un parapluie.¹⁴⁷ Pour tenir compte de ces nouvelles connaissances, notre tableau révisé doit comporter les chiffres suivants :

	Umbrella	No umbrella
Rainy		0
Dry		0
Total	1	0

En d’autres termes, les faits ont éliminé toute possibilité de «ne pas prendre de parapluie », nous devons donc mettre des zéros dans toutes les cases du tableau qui impliquent que je ne prends pas de parapluie. Maintenant que vous savez que je prends un parapluie, la somme de la colonne de gauche doit être 1 pour décrire correctement le fait que P(umbrella)=1.

Quels sont les deux nombres à mettre dans les cellules vides ? Encore une fois, ne nous préoccupons pas des mathématiques, mais pensons plutôt à nos intuitions. Lorsque nous avons rédigé notre tableau la première fois, il s’est avéré que ces deux cellules avaient des nombres presque identiques. Nous avons calculé que la probabilité commune de « pluie et parapluie » était de 4,5%, et la probabilité commune de « temps sec et parapluie » de 4,25%. En d’autres termes, avant de vous dire que je porte en fait un parapluie, vous auriez dit que ces deux événements étaient de probabilité presque identiques. Mais remarquez que ces deux possibilités sont cohérentes avec le fait que je prends un parapluie. Du point de vue de ces deux possibilités, très peu de choses ont changé. J’espère que vous conviendrez qu’il est toujours vrai que ces deux possibilités sont tout aussi plausibles. Nous nous attendons donc à voir dans notre tableau final quelques chiffres qui préservent le fait que « pluie et parapluie » est légèrement plus plausible que « sec et parapluie », tout en assurant que les chiffres dans le tableau s’additionnent. Quelque chose comme ça, peut-être ?

	Umbrella	No Umbrella
Rainy	0.514	0
Dry	0.486	0
Dry day	1	0

Ce que ce tableau vous dit, c’est qu’après avoir appris que je prends un parapluie, vous croyez qu’il y a 51,4 p.100 de chances qu’aujourd’hui soit un jour de pluie, et 48,6 p.100 de chances qu’il ne le soit pas. C’est la réponse à notre problème ! La probabilité à posteriori de pluie P(h|d) étant donné que je prends un parapluie est de 51,4%.

Comment ai-je calculé ces chiffres ? Vous pouvez probablement le deviner. Pour calculer qu’il y avait une probabilité de 0,514 de « pluie », je n’ai fait que prendre la probabilité de 0,045 de « pluie et parapluie » et la diviser par la probabilité de 0,0875 de « parapluie ». Il en résulte un tableau qui répond à notre besoin d’avoir la somme total de 1, et à notre besoin de ne pas interférer avec la plausibilité relative des deux événements qui sont en fait compatibles avec les données. Pour dire la même chose en utilisant un jargon statistique fantaisiste, ce que j’ai fait ici est de diviser la probabilité commune de l’hypothèse et des données P(d,h) par la probabilité marginale des données P(d), et c’est ce qui nous donne la probabilité à posteriori de l’hypothèse étant donné les données qui ont été observées que nous pouvons écrire sous forme d’équation¹⁴⁸

\[ P\left( h \middle| d \right) = \frac{P(d,h)}{P(d)} \]

Cependant, vous vous rappelez ce que j’ai dit au début de la dernière section que la probabilité commune P(d,h) est calculée en multipliant le P(h) précédent par la probabilité \(P(d \mid h)\). Dans la vraie vie, les choses que nous savons vraiment notées sont les a priori et les probabilités, alors substituons-les dans l’équation. Cela nous donne la formule suivante pour la probabilité à posteriori

\[ P\left( h \middle| d \right) = \frac{P(d|h)P(h)}{P(d)} \]

Et cette formule, les amis, est connue sous le nom de règle de Bayes. Elle décrit comment un apprenant commence avec des croyances à piorir sur la plausibilité de différentes hypothèses, et vous dit comment ces croyances devraient être révisées face aux données. Dans le paradigme bayésien, toute inférence statistique découle de cette règle simple.

16.2 Tests d’hypothèses bayésiennes

Au chapitre 9, j’ai décrit l’approche orthodoxe de la vérification des hypothèses. Il a fallu un chapitre entier pour le décrire, parce que la vérification d’hypothèses nulles est une machinerie très élaborée que les gens trouvent très difficile à comprendre. En revanche, l’approche bayésienne de la vérification des hypothèses est incroyablement simple. Prenons des paramètres très proches du scénario orthodoxe. Il y a deux hypothèses que nous voulons comparer, une hypothèse nulle h₀ et une hypothèse alternative h₁. Avant de lancer l’expérience, nous avons quelques croyances P(h) sur les hypothèses qui sont vraies. Nous faisons une expérience et obtenons des données d. Contrairement aux statistiques fréquentistes, les statistiques bayésiennes nous permettent de parler de la probabilité que l’hypothèse nulle soit vraie. Mieux encore, il permet de calculer la probabilité à postériori de l’hypothèse nulle, en utilisant la règle de Bayes

\[ P\left( h_{0} \middle| d \right) = \frac{P(d|h_{0})P(h_{0})}{P(d)} \]

Cette formule nous dit exactement comment quantifier la croyance nous devrions avoir dans l’hypothèse nulle après avoir observé les données d. De même, nous pouvons calculer comment quantifier la croyance nous devons placer dans l’hypothèse alternative en utilisant pour presque la même équation. Tout ce qu’on fait, c’est changer l’indice

\[ P\left( h_{1} \middle| d \right) = \frac{P(d|h_{1})P(h_{1})}{P(d)} \]

C’est si simple que je me sens comme un idiot de prendre la peine d’écrire ces équations. Je ne fais que copier la règle de Bayes de la section précédente¹⁴⁹.

16.2.1 Le facteur Bayes

En pratique, la plupart des analystes bayésiens de données ont tendance à ne pas parler en termes de probabilités à posteriori brutes \(P(h_{0}\mid d)\) et \(P(h_{1}\mid d)\). Nous avons plutôt tendance à parler en termes de risque relatif à postériori (posterior odds ratio). Pensez-y comme un pari. Supposons, par exemple, que la probabilité à postériori de l’hypothèse nulle soit de 25 % et que la probabilité à postériori de l’alternative soit de 75 %. L’hypothèse alternative est trois fois plus probable que l’hypothèse nulle, donc nous disons que le risque relatif est de 3:1 en faveur de l’alternative. Mathématiquement, tout ce que nous avons à faire pour calculer le risque relatif à poseriori est de diviser une probabilité a posteriori par l’autre.

\[ \frac{P\left( h_{1} \middle| d \right)}{P\left( h_{0} \middle| d \right)} = \frac{0,75}{0,25} = 3 \]

Ou, pour écrire la même chose en termes des équations ci-dessus

\[ \frac{P\left( h_{1} \middle| d \right)}{P\left( h_{0} \middle| d \right)} = \frac{P(d|h_{1})}{P(d|h_{0}} \times \frac{P(h_{1})}{P(h_{0})} \]

En fait, cette équation vaut la peine d’être développée. Il y a ici trois termes différents que vous devriez connaitre. Sur le côté gauche, nous avons le risque relatif a posterori (Posterior odds ou ratio a posteriori), qui vous dit ce que vous pensez de la plausibilité relative de l’hypothèse nulle et de l’hypothèse alternative après avoir vu les données. Sur le côté droit, nous avons le ratio des probabilités a priori (Prior odds), qui indiquent ce que vous pensiez avant de voir les données. Au milieu, nous avons le facteur Bayes, qui décrit la quantité de preuves fournies par les données.

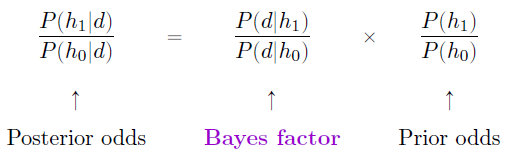
Le facteur Bayes (parfois abrégé en BF) occupe une place particulière dans les tests d’hypothèse bayésiens, car il joue un rôle similaire à la valeur p dans les tests d’hypothèse orthodoxes. Le facteur Bayes quantifie la force des preuves fournies par les données et, à ce titre, c’est le facteur Bayes que les gens ont tendance à déclarer lorsqu’ils font un test d’hypothèse bayésien. La raison pour laquelle les facteurs Bayes sont rapportés plutôt que les ratios a posteriori est que les chercheurs n’ont pas tous les mêmes a priori. Certaines personnes peuvent avoir un préjugé fort pour croire que l’hypothèse nulle est vraie, d’autres peuvent avoir un préjugé fort pour croire qu’elle est fausse. Pour cette raison, la façon polie qu’un chercheur sérieux doit adopter, c’est de déclarer le facteur Bayes. De cette façon, quiconque lit le journal peut multiplier le facteur Bayes par ses propres probabilités a priori personnelles et déterminer par lui-même quelles seraient les ratios a porteriori. Quoi qu’il en soit, par convention, nous aimons prétendre que nous accordons la même importance à l’hypothèse nulle et à l’alternative, auquel cas la probabilité a priori est égale à 1, et le ratio a posteriori est égal au facteur Bayes.

16.2.2 Interprétation des facteurs Bayes

L’un des aspects les plus intéressants du facteur Bayes, c’est que les chiffres sont intrinsèquement significatifs. Si vous faites une expérience et que vous calculez un facteur Bayes de 4, cela signifie que la preuve fournie par vos données correspond à un risque relatif de 4:1 en faveur de l’alternative. Toutefois, certains auteurs ont tenté de quantifier des valeurs normatives de preuve qui seraient considérées comme significatives dans un contexte scientifique. Les deux plus largement utilisés sont ceux de Jeffreys (1998) et Kass et Raftery (1995). Entre les deux, j’ai tendance à préférer le tableau de Kass et al (1995) (1995) parce qu’il est un peu plus conservateur. Le voici :

Bayes factor	Interpretation
1-3	Negligible evidence
3-20	Positive evidence
20-150	Strong evidence
>150	Very strong evidence

Et pour être tout à fait honnête, je pense que même les normes de Kass et al (1995) sont un peu charitables. Si ça ne tenait qu’à moi, j’aurais appelé la catégorie « preuves positives » « preuves faibles ». Pour moi, tout ce qui se situe entre 3:1 et 20:1 est au mieux une preuve « faible » ou « modeste ». Mais il n’y a pas de règle absolue. Ce qui compte comme preuve forte ou faible dépend entièrement de votre prudence et des normes sur lesquelles votre communauté insiste avant de vouloir qualifier une conclusion de « vraie ».

Quoi qu’il en soit, notez que tous les chiffres énumérés ci-dessus ont un sens si le facteur Bayes est supérieur à 1 (c.-à-d. que les données probantes favorisent l’hypothèse alternative). Cependant, l’un des grands avantages pratiques de l’approche bayésienne par rapport à l’approche orthodoxe est qu’elle permet également de quantifier les preuves en faveur de l’hypothèse nulle. Vous pouvez choisir de déclarer un facteur Bayes inférieur à 1, mais pour être honnête, je trouve cela déroutant. Par exemple, supposons que la probabilité des données sous l’hypothèse nulle \(P(d \mid h_{0})\) est égale à 0,2, et que la probabilité correspondante \(P(d \mid h_{1})\) sous l’hypothèse alternative est 0,1. En utilisant les équations données ci-dessus, le facteur de Bayes ici serait

\[ BF = \frac{P(d|h_{1})}{P(d|h_{0})} = \frac{0,1}{0,2} = 0,5 \]

Si on lit littéralement, ce résultat indique que les preuves en faveur de l’alternative sont de 0,5 à 1, ce que je trouve difficile à comprendre. Pour moi, il est beaucoup plus logique de renverser l’équation et de rapporter le montant de la preuve op en faveur de la l’hypothèse nulle. En d’autres termes, ce que nous calculons est

\[ BF' = \frac{P(d|h_{0})}{P(d|h_{1})} = \frac{0,2}{0,1} = 2 \]

Et ce que nous signalons, c’est un facteur Bayes de 2:1 en faveur de l’hypothèse nulle. Beaucoup plus facile à comprendre, et vous pouvez l’interpréter à l’aide du tableau ci-dessus.

16.3 Pourquoi être Bayésien ?

Jusqu’à présent, je me suis concentré exclusivement sur la logique qui sous-tend les statistiques bayésiennes. Nous avons parlé de l’idée de la « probabilité comme degré de croyance », et de ce qu’elle implique sur la façon dont un agent rationnel devrait raisonner le monde. La question à laquelle vous devez répondre vous-même est la suivante : comment voulez-vous faire vos statistiques ? Voulez-vous être un statisticien orthodoxe qui se fie aux distributions d’échantillonnage et aux valeurs p pour guider ses décisions ? Ou voulez-vous être un Bayésien, en vous appuyant sur des choses comme les croyances à priori, les facteurs Bayes et les règles de révision rationnelle des croyances ? Pour être tout à fait honnête, je ne peux pas répondre à cette question pour vous. En fin de compte, cela dépend de ce que vous pensez être juste. C’est votre décision et votre décision seule. Cela dit, je peux vous expliquer un peu pourquoi je préfère l’approche bayésienne.

16.3.1 Des statistiques qui signifient ce que vous pensez qu’elles signifient

Tu n’arrêtes pas d’utiliser ce mot. Je ne pense pas que ça veuille dire ce que tu penses que ça veut dire. - Inigo Montoya, La princesse mariée¹⁵⁰

Pour moi, l’un des plus grands avantages de l’approche bayésienne est qu’elle répond aux bonnes questions. Dans le cadre bayésien, il est tout à fait raisonnable et possible de faire référence à « la probabilité qu’une hypothèse soit vraie ». Vous pouvez même essayer de calculer cette probabilité. En fin de compte, n’est-ce pas ce que vous voulez que vos tests statistiques vous disent ? Pour un être humain, cela semble être l’objectif des statistiques, c’est-à-dire de déterminer ce qui est vrai et ce qui ne l’est pas. Chaque fois que vous n’êtes pas sûr de ce qu’est la vérité, vous devriez utiliser le langage de la théorie des probabilités pour dire des choses comme « il y a 80% de chances que la théorie A soit vraie, mais 20% de chances que la théorie B soit vraie à la place ». Cela semble si évident pour un humain, mais c’est pourtant explicitement interdit dans le cadre orthodoxe. Pour un fréquentiste, de telles affirmations sont un non-sens car « la théorie est vraie » n’est pas un événement répétable. Une théorie est vraie ou elle ne l’est pas, et aucune déclaration probabiliste n’est permise, peu importe de quel point vous voulez le faire. Il y a une raison pour laquelle, à la section 9.5, je vous ai averti à plusieurs reprises de ne pas interpréter la valeur p comme la probabilité que l’hypothèse nulle soit vraie. Il y a une raison pour laquelle presque tous les manuels de statistiques sont obligés de répéter cet avertissement. C’est parce que les gens veulent désespérément que ce soit la bonne interprétation. Malgré le dogme frequentiste, une vie entière d’expérience dans l’enseignement aux étudiants de premier cycle et dans l’analyse de données sur une base quotidienne me suggère que la plupart des humains pensent que « la probabilité que l’hypothèse soit vraie » n’est pas seulement du sens, c’est l’idée à laquelle nous tenons le plus. C’est une idée tellement séduisante que même des statisticiens formés sont victimes de l’erreur d’essayer d’interpréter une valeur p de cette façon. Par exemple, voici une citation d’un rapport officiel de Newspoll en 2013, expliquant comment interpréter l’analyse de leurs données (fréquentistes) :¹⁵¹

Tout au long du rapport, des changements statistiquement significatifs ont été notés, le cas échéant. Tous les tests de signification ont été basés sur le niveau de confiance de 95 %. Cela signifie que si un changement est noté comme étant statistiquement significatif, il y a une probabilité de 95 % qu’un changement réel se soit produit, et non simplement dû à une variation aléatoire. (non souligné dans l’original)

Non ! Ce n’est pas ce que p<.05 signifie. Ce n’est pas ce que 95 % de confiance signifie pour un statisticien fréquentiste. La phrase en gras est tout simplement fausse. Les méthodes orthodoxes ne peuvent pas vous dire « qu’il y a 95% de chances qu’un changement réel se soit produit », car ce n’est pas le genre d’événement auquel les probabilités fréquentistes peuvent être attribuées. Pour un théoricien fréquentiste, cette phrase devrait être dénuée de sens. Même si vous êtes un fréquentiste plus pragmatique, c’est toujours la mauvaise définition d’une valeur p. Il n’est tout simplement pas permis ou correct de dire des choses si l’on veut se fier à des outils statistiques orthodoxes.

D’un autre côté, supposons que vous soyez Bayésien. Bien que le passage en gras soit la mauvaise définition d’une valeur p, c’est à peu près exactement ce que ceut dire un Bayésien lorsqu’on dit que la probabilité à posteriori de l’hypothèse alternative est supérieure à 95%. Voilà le truc. Si le la probabilité à postérioiri du bayésien est réellement ce que vous vous voulez, pourquoi essayer d’utiliser des méthodes orthodoxes ? Si vous voulez faire des affirmations bayésiennes, tout ce que vous avez à faire est d’être un Bayésien et d’utiliser des outils bayésiens.

Pour ma part, j’ai trouvé que passer à la vision bayésienne était le point de vue le plus libérateur. Une fois que vous avez sauté le pas, vous n’avez plus à vous soucier des définitions contre-intuitives des valeurs p. Vous n’avez pas besoin de vous rappeler pourquoi vous ne pouvez pas dire que vous êtes sûr à 95 % que la vraie moyenne se situe dans un certain intervalle. Tout ce que vous avez à faire, c’est d’être honnête sur ce que vous croyiez avant de mener l’étude et de rapporter ce que vous avez appris en le faisant. Ça a l’air sympa, n’est-ce pas ? Pour moi, c’est la grande promesse de l’approche bayésienne. Vous faites l’analyse que vous voulez vraiment faire et vous exprimez ce que vous croyez vraiment que les données vous disent.

16.3.2 Des normes de preuve auxquelles vous pouvez croire

Si [p] est inférieur à .02, il est fortement suggéré que l’hypothèse [nulle] ne correspond pas à l’ensemble des faits. Nous ne nous égarerons pas souvent si nous traçons une ligne conventionnelle à .05 et en considérant que [de plus petites valeurs de p] indiquent un écart réel. - Sir Ronald Fisher (1925)

Considérons la citation ci-dessus de Sir Ronald Fisher, l’un des fondateurs de ce qui est devenu l’approche orthodoxe de la statistique. Si quelqu’un a déjà eu le droit d’exprimer une opinion sur la fonction prévue des valeurs p, c’est bien Fisher. Dans ce passage, tiré de son guide classique Statistical Methods for Research Workers, il est assez clair sur ce que signifie le rejet d’une hypothèse nulle à p<.05. A son avis, si nous prenons p<.05 pour signifier qu’il y a « un effet réel », alors « nous ne serons pas souvent égarés ». Ce point de vue n’est pas inhabituel. D’après mon expérience, la plupart des praticiens expriment des points de vue très semblables à ceux de Fisher. Essentiellement, la p<.05 est supposée représenter une norme de preuve assez stricte.

Quelle est la réalité de cela ? Une façon d’aborder cette question est d’essayer de convertir les valeurs p en facteurs Bayes et de voir comment on peut comparer les deux. Ce n’est pas une chose facile à faire parce qu’une valeur p est un type de calcul fondamentalement différent d’un facteur Bayes, et ils ne mesurent pas la même chose. Cependant, il y a eu quelques tentatives pour établir la relation entre les deux, et c’est quelque peu surprenant. Par exemple, Johnson (2013) présente un cas assez convaincant où (du moins pour les tests t) la p< .05 correspond approximativement à un facteur Bayes compris entre 3:1 et 5:1 en faveur de l’alternative. Si c’est vrai, alors la proposition de Fisher est un peu exagérée. Supposons que l’hypothèse nulle soit vraie environ la moitié du temps (c.-à-d. que la probabilité antérieure de H₀ est de 0,5), et que nous utilisons ces nombres pour calculer la probabilité a posteriori de l’hypothèse nulle puisqu’elle a été rejetée à p<.05. En utilisant les données de Johnson (2013), nous voyons que si vous rejetez l’hypothèse nulle à p< .05, vous aurez raison environ 80% du temps. Je ne sais pas ce que vous en pensez, mais, à mon avis, une norme de preuve qui garantit que vous vous trompez sur 20 % de vos décisions n’est pas suffisante. Il n’en demeure pas moins que, tout à fait contrairement à ce que prétend Fisher, si vous rejetez à p<.05 vous vous égarerez très souvent. Ce n’est pas du tout un seuil de preuve très strict.

16.3.3 La valeur p est un mensonge.

Le gâteau est un mensonge. Le gâteau est un mensonge. Le gâteau est un mensonge. Le gâteau est un mensonge. - Portal¹⁵²

Bien, à ce stade, vous pensez peut-être que le vrai problème ne vient pas des statistiques orthodoxes, mais juste du p<.05 standard. En un sens, c’est vrai. La recommandation de Johnson (2013) n’est pas que « tout le monde doit être bayésien à partir de maintenant ». Au contraire, la suggestion est qu’il serait plus sage de changer la norme conventionnelle et de choisir un niveau comme un p < .01. Ce n’est pas un point de vue déraisonnable, mais à mon sens, le problème est un peu plus grave que cela. À mon avis, il y a un assez gros problème dans la construction de la plupart (mais pas tous) les tests d’hypothèses orthodoxes. Ils sont tout à fait naïfs quant à la façon dont les humains font de la recherche, et c’est pour cette raison que la plupart des valeurs p sont fausses.

Cela vous parait une affirmation absurde ? Eh bien, considérez le scénario suivant. Vous avez formulé une hypothèse de recherche très intéressante et vous concevez une étude pour la mettre à l’épreuve. Vous êtes très diligent, alors vous effectuez une analyse de puissance pour déterminer quelle devrait être la taille de votre échantillon, et vous effectuez l’étude. Vous exécutez votre test d’hypothèse et vous obtenez une valeur p de 0,072. Vraiment très ennuyeux, non ?

Que devriez-vous faire ? Voici quelques possibilités :

Vous concluez qu’il n’y a pas d’effet et essayez de le publier comme résultat nul.
Vous supposez qu’il pourrait y avoir un effet et essayez de le publier comme un résultat « significatif limite ».
Vous abandonnez et essayez une nouvelle étude
Vous collectez quelques données supplémentaires pour voir si la valeur de p augmente ou (de préférence !) descend en dessous du critère « magique » de p<.05

Laquelle choisiriez-vous ? Avant de poursuivre la lecture, je vous invite à prendre le temps d’y réfléchir. Soyez honnête avec vous-même. Mais n’en faites pas trop, parce que vous êtes foutu, peu importe ce que vous choisissez. En me basant sur mes propres expériences en tant qu’auteur, rélecteur et éditeur, ainsi que sur les histoires que j’ai entendues d’autres personnes, voici ce qui va se passer dans chaque cas :

Commençons par l’option 1. Si vous essayez de le publier comme résultat nul, l’article aura du mal à être publié. Certains critiques penseront que p = .072 n’est pas vraiment un résultat nul. Ils diront que c’est à la limite de l’important. D’autres examinateurs conviendront qu’il s’agit d’un résultat nul, mais prétendront que même si certains résultats nuls sont publiables, le vôtre ne l’est pas. Un ou deux relecteurs peuvent même être de votre côté, mais vous devrez livrer une bataille ardue pour y arriver.
Réfléchissons à l’option numéro 2. Supposons que vous essayez de le publier comme un résultat significatif limite. Certains critiques diront qu’il s’agit d’un résultat nul et qu’il ne devrait pas être publié. D’autres prétendront que les preuves sont ambiguës et que vous devriez recueillir plus de données jusqu’à ce que vous obteniez un résultat significatif clair. Encore une fois, le processus de publication n’est pas de votre côté.
Compte tenu des difficultés à publier un résultat « ambigu » comme p = .072, l’option numéro 3 peut sembler tentante : abandonner et faire autre chose. Mais c’est la recette du suicide professionnel. Si vous abandonnez et essayez un nouveau projet chaque fois que vous vous trouvez face à une ambiguïté, votre travail ne sera jamais publié. Et si vous êtes dans le milieu universitaire sans avoir publié d’articles, vous pouvez perdre votre emploi. Donc, cette option n’existe pas.
On dirait que vous êtes coincé avec l’option 4. Vous n’avez pas de résultats concluants, alors vous décidez de recueillir d’autres données et de réexécuter l’analyse. Cela semble raisonnable, mais malheureusement pour vous, si vous faites cela, toutes vos valeurs p sont maintenant incorrectes. Toutes les trois. Pas seulement les valeurs p que vous avez calculées pour cette étude. Toutes les trois. Toutes les valeurs p que vous avez calculées dans le passé et toutes les valeurs p que vous calculerez dans le futur. Heureusement, personne ne le remarquera. Vous serez publié, et vous aurez menti.

Mais attendez ! Comment cette dernière partie peut-elle être vraie ? Je veux dire, ça semble être une stratégie parfaitement raisonnable. Vous avez recueilli des données, les résultats n’étaient pas concluants, alors maintenant ce que vous voulez faire, c’est recueillir plus de données jusqu’à ce que les résultats soient concluants. Qu’est-ce qu’il y a de mal à ça ?

Honnêtement, il n’y a rien de mal à ça. C’est une chose raisonnable, raisonnable et rationnelle à faire. Dans la vraie vie, c’est exactement ce que chaque chercheur fait. Malheureusement, la théorie des tests d’hypothèse nulle telle que je l’ai décrite au chapitre 9 vous interdit de le faire. La raison¹⁵³ est que la théorie suppose que l’expérience est terminée et que toutes les données sont disponibles. Parce qu’elle suppose que l’expérience est terminée, elle n’envisage que deux décisions possibles. Si vous utilisez la méthode conventionnelle p<.05, ces décisions sont :

Outcomes	Action
p less than .05	Reject the null
p greater than .05	Retain the null

Ce que vous faites, c’est ajouter une troisième action possible au problème de prise de décision. Plus précisément, ce que vous faites, c’est d’utiliser la valeur p elle-même comme raison pour justifier la poursuite de l’expérience. Par conséquent, vous avez transformé la procédure de prise de décision en une procédure qui ressemble davantage à celle-ci :

Outcomes	Action
p less than .05	Reject the null
p between .05 and 1	Continue the experiment
p greater than 1	Stop the experiment and retain the null

La théorie « de base » des tests d’hypothèse nulle n’est pas construite pour gérer ce genre de choses, pas sous la forme que j’ai décrite au chapitre 9. Si vous êtes le genre de personne qui choisirait de « collecter plus de données » dans la vie réelle, cela implique que vous ne prenez pas de décisions en accord avec les règles du test d’hypothèse nulle. Même si vous arrivez à la même décision que le test d’hypothèse, vous ne suivez pas le processus de décision qu’il implique, et c’est cette incapacité à suivre le processus qui pose problème.¹⁵⁴ Vos valeurs p sont des mensonges.

Pire encore, c’est un mensonge dangereux, parce qu’ils sont tous trop petits. Pour vous donner une idée de la gravité de la situation, considérez le scénario suivant (le pire des cas). Imaginez que vous êtes un vrai un chercheur super enthousiaste avec un budget serré qui n’a pas prêté attention à mes mises en garde ci-dessus.

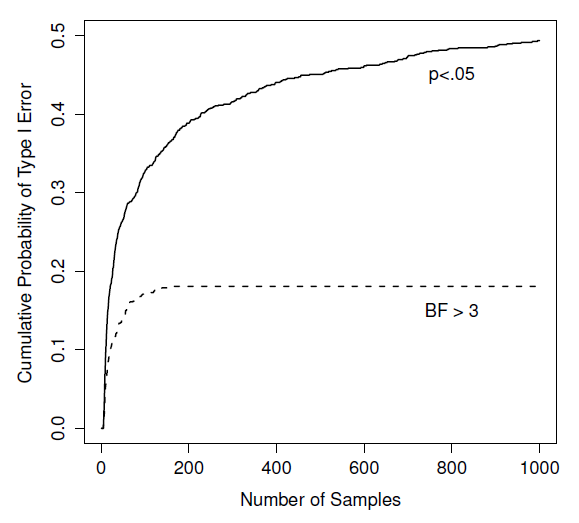
Figure 16‑1 : Dans quelle mesure les choses peuvent-elles mal tourner si vous réexécutez vos tests chaque fois que de nouvelles données arrivent ? Si vous êtes un fréquentiste, la réponse est « très mauvaise ».

Vous concevez une étude comparant deux groupes. Vous voulez désespérément voir un résultat significatif à la p < .05, mais vous ne voulez vraiment pas collecter plus de données qu’il n’en faut (parce que c’est cher). Afin de réduire les coûts, vous commencez à collecter des données, mais chaque fois qu’une nouvelle observation arrive, vous effectuez un test t sur vos données. Si le test t donne p<.05, vous arrêtez l’expérience et rapportez un résultat significatif. Si ce n’est pas le cas, vous continuez à collecter des données. Vous continuez à le faire jusqu’à ce que vous atteigniez votre limite de dépenses prédéfinie pour cette expérience. Supposons que cette limite s’applique à N=1000 observations. Il s’avère que la vérité est qu’il n’y a pas d’effet réel à trouver : l’hypothèse nulle est vraie. Alors, quelle est la probabilité que vous arriviez à la fin de l’expérience et que vous concluiez (correctement) qu’il n’y a aucun effet ? Dans un monde idéal, la réponse ici devrait être 95%. Après tout, l’intérêt de la p< .05 est de contrôler le taux d’erreur de type I à 5 %, alors ce que nous espérons, c’est qu’il n’y a que 5 % de chances de rejeter faussement l’hypothèse nulle dans cette situation. Cependant, il n’y a aucune garantie que ce soit vrai. Vous enfreignez les règles. Parce que vous effectuez des tests de façon répétée, en jetant un coup d’oeil à vos données pour voir si vous avez obtenu un résultat significatif, tous les paris sont annulés.

A quel point est-ce grave? La réponse est représentée par la ligne noire pleine de la Figure 16‑1, et c’est incroyablement mauvais. Si vous jetez un coup d’oeil à vos données après chaque observation, il y a 49% de chance que vous fassiez une erreur de type I. C’est, euh, un peu plus que les 5% que vous devriez avoir. A titre de comparaison, imaginez que vous avez utilisé la stratégie suivante. Vous commencez à recueillir des données. Chaque fois qu’une observation arrive, effectuez un test t bayésien (section 16.4) et examinez le facteur Bayes. Je suppose que Johnson (2013) a raison, et je traiterai un facteur de Bayes de 3:1 comme étant à peu près équivalent à une valeur p de 0,05.¹⁵⁵ Cette fois-ci, notre chercheur à la gâchette heureuse utilise la procédure suivante. Si le facteur de Bayes est de 3:1 ou plus en faveur de la l’hypothèse nulle, vous arrêter l’expérience et conserver la valeur nulle. S’il est de 3:1 ou plus en faveur de l’alternative, vous arrêtez l’expérience et rejetez l’hypothèse nulle. Dans le cas contraire, vous continuez le test. Maintenant, comme la dernière fois, supposons que l’hypothèse nulle soit vraie. Que se passe-t-il ? Il se trouve que j’ai également effectué les simulations pour ce scénario, et les résultats sont représentés par la ligne pointillée de la Figure 16‑1. Il s’avère que le taux d’erreur de type I est beaucoup plus faible que le taux de 49 % que nous obtenions en utilisant le test t orthodoxe.

D’une certaine façon, c’est remarquable. Le but des tests d’hypothèse nulle orthodoxes est de contrôler le taux d’erreur de type I. Les méthodes bayésiennes ne sont pas du tout conçues pour cela. Or, il s’avère que, face à un chercheur à la « gâchette heureuse » qui continue à faire des tests d’hypothèse au fur et à mesure que les données arrivent, l’approche bayésienne est beaucoup plus efficace. Même la norme 3:1, que la plupart des Bayésiens considéreraient comme inacceptablement laxiste, est beaucoup plus sûre que la norme p<.05.

16.3.4 C’est vraiment si grave ?

L’exemple que j’ai donné dans la section précédente est une situation assez extrême. Dans la vraie vie, les gens ne font pas de tests d’hypothèse chaque fois qu’une nouvelle observation arrive. Il n’est donc pas juste de dire que la p>.05 correspond à un taux d’erreur de type I de 49 % (c.-à-d., p=.49). Mais le fait est que si vous voulez que vos valeurs p soient honnêtes, vous devez soit changer complètement la façon de faire des tests d’hypothèse, soit appliquer une règle stricte de ne pas regarder avant. Vous n’êtes pas autorisé à utiliser les données pour décider quand mettre fin à l’expérience. Vous n’êtes pas autorisé à regarder une valeur p « limite » et à décider de collecter plus de données. Vous n’êtes même pas autorisé à modifier votre stratégie d’analyse de données après avoir examiné les données. Vous êtes strictement tenu de suivre ces règles, sinon les valeurs p que vous calculerez seront absurdes.

Oui, ces règles sont étonnamment strictes. En classe, il y a quelques années, j’ai demandé aux élèves de réfléchir à ce scénario. Supposons que vous avez commencé votre étude avec l’intention de collecter N = 80 personnes. Au début de l’étude, vous suivez les règles, refusant d’examiner les données ou d’effectuer des tests. Mais quand vous atteignez N = 50, votre volonté cède et vous jetez un coup d’oeil. Et là surprise, vous avez un résultat significatif ! Bien sûr, vous aviez dit que vous continueriez à mener l’étude jusqu’à une taille d’échantillon de N=80, mais cela semble un peu inutile maintenant. Le résultat est significatif avec une taille d’échantillon de N = 50, donc à quoi servirait de continuer à collecter des données ? N’êtes-vous pas tenté d’arrêter ? Juste un peu ? N’oubliez pas que si c’est le cas, votre taux d’erreur de type I à p> .05 vient de s’envoler à 8%. Lorsque vous rendez compte dans votre journal de p>.05 dans votre journal, ce que vous êtes en train de dire en vrai, c’est p<.08. Cela illustre à quel point les conséquences « d’un simple coup d’oeil » peuvent être graves.

Considérez maintenant que la littérature scientifique est remplie de tests t, d’analyses de variance, de régressions et de tests khi-deux. Quand j’ai écrit ce livre, je n’ai pas choisi ces tests arbitrairement. La raison pour laquelle ces quatre outils apparaissent dans la plupart des textes d’introduction à la statistique est qu’il s’agit des outils de base en science. Aucun de ces outils n’inclut de correction pour faire face au « coup d’œil dans les données » : ils supposent tous que vous ne le faites pas. Mais dans quelle mesure cette hypothèse est réaliste ? Dans la vie réelle, combien de personnes, selon vous, ont « jeté un coup d’œil » à leurs données avant la fin de l’expérience et adapté leur comportement ultérieur après avoir vu à quoi elles ressemblaient ? Sauf lorsque la procédure d’échantillonnage est fixée par une contrainte externe, je suppose que la réponse est « la plupart des gens l’ont fait ». Si cela s’est produit, vous pouvez en déduire que les valeurs de p rapportées sont fausses. Pire encore, comme nous ne savons pas quel processus de décision ils ont suivi, nous n’avons aucun moyen de savoir quelles auraient dû être les valeurs p. Vous ne pouvez pas calculer une valeur p si vous ne connaissez pas la procédure de prise de décision utilisée par le chercheur. Il s’en suit que la valeur p rapportée n’est pas fiable.

Compte tenu de tout ce qui précède, quel est le message à retenir ? Ce n’est pas que les méthodes bayésiennes sont infaillibles. Si un chercheur est déterminé à tricher, il peut toujours le faire. La règle de Bayes ne peut pas empêcher les gens de mentir, ni les empêcher de truquer une expérience. Ce n’est pas ce que je veux dire. Mon argument est le même que celui que j’ai fait valoir au tout début du livre à la section 1.1 : la raison pour laquelle nous faisons des tests statistiques est de nous protéger de nous-mêmes. Et la raison pour laquelle « l’examen des données » est une telle préoccupation, c’est qu’il est si tentant, même pour les chercheurs honnêtes. Une théorie de l’inférence statistique doit le reconnaître. Oui, vous pourriez essayer de défendre les valeurs p en disant que c’est la faute du chercheur s’il ne les utilise pas correctement, mais à mon avis, ce n’est pas la question. Une théorie de l’inférence statistique qui est tellement naïve à l’égard des humains qu’elle ne tient même pas compte de la possibilité que le chercheur puisse examiner ses propres données n’est pas une théorie valable. La citation suivante résume ce que je veux dire essentiellement :

Les bonnes lois ont leur origine dans les mauvaises moeurs. - Ambrosius Macrobius¹⁵⁶

De bonnes règles pour les tests statistiques doivent reconnaître la fragilité humaine. Aucun de nous n’est sans péché. Aucun de nous n’est à l’abri de la tentation. Un bon système d’inférence statistique devrait fonctionner même lorsqu’il est utilisé par de vrais humains. Les tests d’hypothèse nulle orthodoxe ne le font pas.¹⁵⁷

16.4 Tests t bayésiens

Un type important de problème d’inférence statistique discuté dans ce livre est la comparaison entre deux moyennes, discutée en détail dans le chapitre sur les tests t (chapitre 11). Si vous vous souvenez bien, il existe plusieurs versions du test t. Je vais parler un peu des versions bayésiennes des tests t pour des échantillons indépendants et pour des échantillons appariés t-tests dans cette section.

16.4.1 Test t pour échantillons indépendants

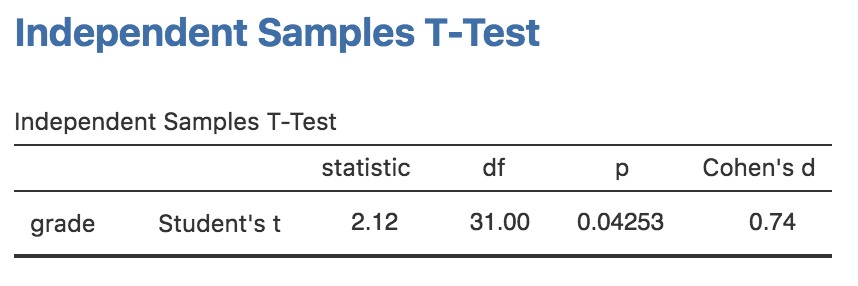
Le type de test t le plus courant est le test t d’échantillons indépendants, et il apparaît lorsque vous disposez de données comme dans l’ensemble de données harpo.csv que nous avons utilisé dans le chapitre précédent sur les tests t (chapitre 11). Dans cet ensemble de données, nous avons deux groupes d’élèves, ceux qui ont reçu des leçons d’Anastasia et ceux qui ont pris leurs cours avec Bernadette. La question à laquelle nous voulons répondre est de savoir s’il y a une différence dans les notes obtenues par ces deux groupes d’élèves. Au chapitre 11, j’ai suggéré d’analyser ce type de données à l’aide du test t pour des Échantillons indépendants dans Jamovi, qui nous a donné les résultats de la Figure 16‑2. Comme nous obtenons une valeur p inférieure à 0,05, nous rejetons l’hypothèse nulle.

Figure 16‑2 : Échantillons indépendants - résultat du test t dans Jamovi

A quoi ressemble la version bayésienne du test t? Nous pouvons obtenir l’analyse du facteur de Bayes en cochant la case « Bayes Factor » sous l’option « Tests », et en acceptant la valeur à priori par défaut suggérée dans l’option « Prior ». Ceci donne les résultats présentés dans le tableau de la Figure 16‑3. Ce que nous obtenons dans ce tableau est une statistique du facteur Bayes de 1,75, ce qui signifie que les preuves fournies par ces données sont d’environ 1,8:1 en faveur de l’hypothèse alternative.

Avant de poursuivre, il convient de souligner la différence entre les résultats des tests orthodoxes et ceux des tests bayésiens. Selon le test orthodoxe, nous avons obtenu un résultat significatif, mais à peine. Néanmoins, beaucoup de gens seraient heureux d’accepter p=.043 comme preuve raisonnablement solide d’un effet. Par contre, notez que le test bayésien n’atteint même pas un seuil de 2:1 en faveur d’un effet, et serait considéré comme une preuve très faible au mieux. D’après mon expérience, c’est un résultat assez typique. Les méthodes bayésiennes exigent habituellement plus de preuves avant de rejeter l’hypothèse nulle.

Figure 16‑3 : Analyse des facteurs Bayes en parallèle avec le test t d’échantillons indépendants

16.4.2 Test t pour échantillons appariés

A la section 11.5, j’ai discuté de l’ensemble de données chico.csv dans lequel les notes des élèves ont été mesurées lors de deux tests, et nous voulions savoir si les notes avaient augmenté du test 1 au test 2. Comme chaque élève a fait les deux tests, l’outil utilisé pour analyser les données était un test t pour des échantillons appariés de tests. La Figure 16‑4 montre le tableau des résultats de Jamovi pour le test t apparié conventionnel à côté de l’analyse du facteur de Bayes. A ce stade, j’espère que vous pourrez lire cette sortie sans aucune difficulté. Les données fournissent des preuves d’environ 6000:1 en faveur de l’alternative. Nous pourrions probablement rejeter l’hypothèse nulle avec un peu plus de confiance !

Figure 16‑4 : Résultats pour un test t pour échantillons appariés et le Facteur de Bayes dans Jamovi

16.5 Résumé

La première moitié de ce chapitre a porté principalement sur les fondements théoriques des statistiques bayésiennes. J’ai présenté les principes mathématiques de fonctionnement de l’inférence bayésienne (section 16.1), et j’ai donné un aperçu très simple de la façon dont la vérification des hypothèses bayésiennes est généralement effectuée (section 16.2). Enfin, j’ai consacré un peu d’espace à expliquer pourquoi je pense que les méthodes bayésiennes valent la peine d’être utilisées (Section 16.3).

Puis j’ai donné un exemple pratique, un t-test bayésien (Section 16.4). Si vous souhaitez en savoir plus sur l’approche bayésienne, il existe de nombreux ouvrages intéressants que vous pouvez consulter. Le livre de John Kruschke, Doing Bayesian Data Analysis, est un bon point de départ (Kruschke 2011) et est un bon mélange de théorie et de pratique. Son approche est un peu différente de celle du « facteur de Bayes » dont j’ai parlé ici, de sorte que vous ne couvrirez pas le même terrain. Si vous êtes un psychologue cognitif, vous voudrez peut-être consulter le livre de Michael Lee et E.J. Wagenmakers intitulé Bayesian Cognitive Modeling (Lee and Wagenmakers 2014). J’ai choisi ces deux livres parce que je pense qu’ils sont particulièrement utiles pour les gens de ma discipline, mais il y a beaucoup de bons livres, alors regardez autour de vous !

References

Jeffreys, Sir Harold. 1998. The Theory of Probability. Third Edition. Oxford Classic Texts in the Physical Sciences. Oxford, New York: Oxford University Press.

Kass, Robert E., and Adrian E. Raftery. 1995. “Bayes Factors.” Journal of the American Statistical Association 90 (430): 773–95. https://doi.org/10.2307/2291091.

Kruschke, John K. 2011. Doing Bayesian Data Analysis: A Tutorial with R and BUGS. Academic Press.

Lee, Michael D., and Eric-Jan Wagenmakers. 2014. Bayesian Cognitive Modeling: A Practical Course. Cambridge University Press.

http://en.wikiquote.org/wiki/David_Hume ↩︎
https://en.wikipedia.org/wiki/Climate_of_Adelaide ↩︎
C’est un acte de foi, je sais, mais il faut s’en accommoder, si vous êtes d’accord↩︎
Je déteste soulever cette question, mais certains statisticiens s’opposeraient à ce que j’utilise le mot “probabilité” ici. Le problème, c’est que le mot “probabilité” a une signification très spécifique dans les statistiques fréquentistes, et ce n’est pas tout à fait la même chose que dans les statistiques bayésiennes. D’après ce que je peux dire, les Bayésiens n’avaient pas à l’origine de nom convenu pour la probabilité, et il est donc devenu pratique courante pour les gens d’utiliser la terminologie fréquentiste. Cela n’aurait pas posé de problème si la façon dont les Bayésiens utilisent le mot ne s’avèrait être très différente de celle des fréquentistes. Ce n’est pas l’endroit pour une autre longue leçon d’histoire, mais, pour le dire grossièrement, quand un Bayésien parle « d’une fonction de vraisemblance », il se réfère habituellement à l’une des lignes du tableau. Quand un fréquentiste dit la même chose, il se réfère au tableau lui-même, mais pour aux « une fonction de vraisemblance » fait référence presque toujours à une des colonnes. Cette distinction est importante dans certains contextes, mais elle ne l’est pas pour notre propos.↩︎
Pour être clair, l’information « à priori » est une connaissance ou une croyance préexistante, avant que nous recueillions ou utilisions toute donnée pour améliorer cette information.↩︎
Si nous étions un peu plus sophistiqués, nous pourrions étendre l’exemple pour tenir compte de la possibilité que je mente au sujet du parapluie. Mais gardons les choses simples, d’accord ?↩︎
Vous remarquerez peut-être que cette équation est en fait une reformulation de la même règle de base que celle que j’ai énoncée au début de la dernière section. Si vous multipliez les deux côtés de l’équation par P(d), alors vous obtenez \(P(d)P(h \mid d)=P(d,h)\), qui est la règle de calcul des probabilités conjointes. Je n’introduis donc pas de « nouvelles » règles ici, j’utilise simplement la même règle d’une manière différente.↩︎
Évidemment, c’est une histoire très simplifiée. Toute la complexité de la vérification des hypothèses bayésiennes dans la vie réelle se résume à la façon dont vous calculez la probabilité P(d|h) lorsque l’hypothèse h est une chose complexe et vague. Je ne vais pas parler de ces complexités dans ce livre, mais je tiens à souligner que même si cette histoire simple est vraie, la vraie vie est plus compliquée que ce que je suis capable de traiter dans un manuel de statistiques d’introduction.↩︎
Je dois noter au passage que je ne suis pas la première personne à utiliser cette citation pour me plaindre des méthodes fréquentistes. Rich Morey et ses collègues ont eu l’idée en premier. Je la vole sans vergogne parce que c’est une citation à utiliser dans ce contexte et je refuse de rater une occasion de citer The Princess Bride.↩︎
http://about.abc.net.au/reports-publications/appreciation-survey-summary-report-2013/↩︎
http://knowyourmeme.com/memes/the-cake-is-a-lie ↩︎
Pour être tout à fait honnête, je dois reconnaître que tous les tests statistiques orthodoxes ne reposent pas sur cette hypothèse stupide. Il existe un certain nombre d’outils d’analyse séquentielle qui sont parfois utilisés dans les essais cliniques et autres. Ces méthodes sont fondées sur l’hypothèse que les données sont analysées au fur et à mesure qu’elles arrivent, et ces tests ne sont pas remis en cause comme je le prétends ici. Cependant, les méthodes d’analyse séquentielle sont construites d’une manière très différente de la version « standard » des tests d’hypothèse nulle. Ils ne sont pas inclus dans les manuels d’introduction, et ils ne sont pas très largement utilisés dans la littérature psychologique. La préoccupation que je soulève ici est valable pour chaque test orthodoxe que j’ai présenté jusqu’ici et pour presque tous les tests que j’ai vus rapportés dans les journaux que j’ai lus.↩︎
Un problème connexe : http://xkcd.com/1478/↩︎
Certains lecteurs pourraient se demander pourquoi j’ai choisi 3:1 plutôt que 5:1, étant donné que Johnson (2013) suggère que p = .05 se trouve quelque part dans cette intervalle. Je l’ai fait dans le but d’être charitable avec la valeur p. Si j’avais choisi un facteur Bayes de 5:1, les résultats seraient encore plus favorables à l’approche bayésienne.↩︎
http://www.quotationspage.com/quotes/Ambrosius_Macrobius/↩︎
Bien sûr, je sais que certains fréquentistes avertis vont lire ceci et commencer à contester les propos de cette section. Je ne suis pas stupide. Je sais parfaitement que si vous adoptez une perspective d’analyse séquentielle, vous pouvez éviter ces erreurs dans le cadre orthodoxe. Je sais aussi que vous pouvez explicitement concevoir des études avec des analyses intermédiaires à l’esprit. Donc oui, dans un sens, j’attaque une version « bouc émissaire » des méthodes orthodoxes. Cependant, le bous émissaire que j’attaque est celui qui est utilisé par presque tous les praticiens. Si jamais les méthodes séquentielles deviennent la norme chez les psychologues expérimentaux et que je ne suis plus obligé de lire 20 analyses de variance extrêmement douteuses par jour, je promets de réécrire cette section et de réduire le vitriol. Mais d’ici là, je maintiens mon affirmation selon laquelle les méthodes utilisant le facteur Bayes par défaut sont beaucoup plus robustes face aux pratiques d’analyse des données telles qu’elles existent dans le monde réel. Les méthodes orthodoxes par défaut craignent, et nous le savons tous.↩︎