Chapitre 7 Introduction à la probabilité
[Dieu] ne nous a accordé que le crépuscule de la Probabilité. - John Locke
Jusqu’à maintenant, nous avons discuté de certaines des idées clés de la conception expérimentale, et nous avons parlé un peu de la façon dont vous pouvez résumer un ensemble de données. Pour beaucoup de gens, c’est tout ce qu’il y a à faire avec les statistiques : recueillir tous les chiffres, calculer les moyennes, dessiner des graphiques et les mettre toutes quelque part dans un rapport. C’est un peu comme la philatélie, mais avec des chiffres. Cependant, les statistiques c’est bien plus que cela. Cependant, les statistiques englobent beaucoup plus que cela. En fait, la statistique descriptive est l’une des plus petites composantes de la statistique et l’une des moins puissantes. La plus importante et la plus utile caractéristique des statistiques est qu’elles fournissent des informations qui vous permettent de faire des inférences sur les données.
Une fois que l’on commence à penser aux statistiques en ces termes, que les statistiques sont là pour nous aider à tirer des conclusions à partir des données, on commence à en voir des exemples partout. Par exemple, voici un petit extrait d’un article paru dans le Sydney Morning Herald (30 octobre 2010) :
« J’ai un travail difficile », a déclaré le Premier ministre en réponse à un sondage qui a révélé que son gouvernement est maintenant l’administration travailliste la plus impopulaire de l’histoire des sondages, avec un vote lors de la primaire de seulement 23 pour cent ».
Ce genre de remarque est tout à fait banale dans les journaux ou dans la vie de tous les jours, mais réfléchissons un peu à ce qu’elle implique. Une société de sondage a effectué une enquête, habituellement assez important parce qu’elle peut se le permettre. Je suis trop paresseux pour restituer l’enquête originale, alors imaginons qu’ils ont appelé 1000 électeurs de Nouvelle-Galles du Sud (NSW) au hasard, et 230 (23%) d’entre eux ont déclaré avoir l’intention de voter pour le Parti travailliste australien (ALP). Pour les élections fédérales de 2010, la Commission électorale australienne a déclaré 4 610 795 électeurs inscrits en Nouvelle-Galles du Sud, de sorte que les opinions des 4 609 795 électeurs restants (environ 99,98 % des électeurs) nous sont inconnues. Même en supposant que personne n’a menti à la société de sondage, la seule chose que nous pouvons dire avec 100% de confiance est que le vrai vote primaire ALP se situe entre 230/4610795 (environ 0,005%) et 4610025/4610795 (environ 99,83%). Alors, sur quelle base est-il légitime pour la société de sondage, le journal et le lectorat de conclure que le vote à la primaire de l’ALP n’est que d’environ 23% ?
La réponse à la question est assez évidente. Si j’appelle 1000 personnes au hasard et que 230 d’entre elles disent qu’elles ont l’intention de voter pour l’ALP, il semble très peu probable qu’il s’agisse des 230 seules personnes sur l’ensemble des électeurs qui ont l’intention de voter. En d’autres termes, nous supposons que les données recueillies par la société de sondage sont assez représentatives de la population en général. Mais quelle représentativité ? Serait-on surpris d’apprendre que le véritable vote à la primaire de l’ALP est en fait de 24% ? 29% ? 37% ? C’est à ce moment-là que l’intuition quotidienne commence à s’effondrer un peu. Personne ne serait surpris de 24 p. 100 et tout le monde serait surpris de 37 p. 100, mais il est un peu difficile de dire si 29 p. 100 est plausible. Nous avons besoin d’outils plus puissants que le simple examen des chiffres et des hypothèses.
Les statistiques inférentielles fournissent les outils dont nous avons besoin pour répondre à ce genre de questions, et puisque ces questions sont au cœur de l’entreprise scientifique, elles occupent la part du lion dans chaque cours d’introduction à la statistique et aux méthodes de recherche. Cependant, la théorie de l’inférence statistique est construite sur la théorie des probabilités. Et c’est vers la théorie des probabilités que nous devons maintenant nous tourner. Cette discussion de la théorie des probabilités est essentiellement un détail de fond. Il n’y a pas beaucoup de statistiques en soi dans ce chapitre, et vous n’avez pas besoin de comprendre ce matériel aussi en profondeur que les autres chapitres de cette partie du livre. Néanmoins, comme la théorie des probabilités sous-tend une grande partie des statistiques, cela vaut la peine d’en aborder certains aspects fondamentaux.
7.1 En quoi la probabilité et les statistiques sont-elles différentes ?
Avant de commencer à parler de la théorie des probabilités, il est utile de réfléchir un moment à la relation entre probabilité et statistiques. Les deux disciplines sont étroitement liées, mais elles ne sont pas identiques. La théorie des probabilités est « la doctrine des chances ». C’est une branche des mathématiques qui vous indique la fréquence à laquelle différents types d’événements se produisent. Par exemple, toutes ces questions sont des choses auxquelles vous pouvez répondre en utilisant la théorie des probabilités :
- Quelles sont les chances qu’une belle pièce de monnaie tombe sur face 10 fois de suite ?
- Si je lance deux fois un dé à six faces, quelle est la probabilité que je lance deux six ?
- Quelle est la probabilité que cinq cartes tirées d’un jeu de cartes parfaitement mélangées soient toutes des cœurs ?
- Quelles sont les chances que je gagne à la loterie ?
Notez que toutes ces questions ont quelque chose en commun. Dans chaque cas, la « vérité du monde » est connue et ma question porte sur le « genre d’événements » qui va se produire. Dans la première question, je sais que la pièce de monnaie est correcte et qu’il y a donc 50 p. 100 de chances que n’importe quelle pièce de monnaie tombe sur pile ou face. Dans la deuxième question, je sais que la chance d’avoir un 6 sur un seul dé est de 1 sur 6. Dans la troisième question, je sais que le jeu est bien mélangé. Et dans la quatrième question, je sais que la loterie suit des règles spécifiques. Vous comprenez l’idée. Le point critique est que les questions probabilistes partent d’un modèle connu du monde, et nous utilisons ce modèle pour faire certains calculs. Le modèle sous-jacent peut être assez simple. Par exemple, dans l’exemple de pile ou face, nous pouvons écrire le modèle comme ceci :
\[ p\left( \text{face} \right) = 0,5 \]
Ce que l’on peut lire comme « la probabilité de face est de 0,5 ». Comme nous le verrons plus loin, de la même façon que les pourcentages sont des nombres qui vont de 0 % à 100 %, les probabilités ne sont que des nombres qui vont de 0 à 1. Lorsque j’utilise ce modèle de probabilité pour répondre à la première question, je ne sais pas exactement ce qui va se passer. J’aurai peut-être 10 faces, comme le dit la question. Mais peut-être que j’aurai trois faces. C’est le point clé. En théorie des probabilités, le modèle est connu, mais les données ne le sont pas.
C’est donc ça, la probabilité. Qu’en est-il des statistiques ? Les questions statistiques fonctionnent dans l’autre sens. Dans les statistiques, nous ne connaissons pas la vérité sur le monde. Tout ce que nous avons, ce sont les données et c’est à partir de ces données que nous voulons apprendre la vérité sur le monde. Les questions statistiques ont tendance à ressembler davantage à celles-ci :
- Si mon ami tire à pile ou face 10 fois et obtient 10 face, est-ce qu’il me joue un tour ? Si cinq cartes sur le dessus du paquet sont toutes des cœurs, quelle est la probabilité que le paquet ait été mélangé ? Si le conjoint du commissaire de la loterie gagne, quelle est la probabilité que la loterie ait été truquée ?
Cette fois, nous n’avons que des données. Ce que je sais, c’est que j’ai vu mon ami tirer à pile ou face 10 fois et qu’à chaque fois, il y a eu des problèmes. Et ce que je veux en déduire, c’est si oui ou non, je dois conclure que ce que je viens de voir est en fait une pièce de monnaie qui a été lancée à pile ou face 10 fois de suite, ou si je dois soupçonner que mon ami me joue un tour. Les données que j’ai ressemblent à ceci :
F F F F F F F F F F
Ce que j’essaie de faire, c’est de trouver en quel « modèle du monde » je dois avoir confiance. Si la pièce est juste alors le modèle que je devrais adopter est celui qui dit que la probabilité de faces est de 0,5, c’est-à-dire \[p\left( \text{face} \right) = 0,5)\]. Si la pièce n’est pas correcte alors je devrais conclure que la probabilité de face n’est pas de 0,5, ce que nous écririons comme \[p(face) \neq 0,5\]. En d’autres termes, le problème de l’inférence statistique consiste à déterminer lequel de ces modèles de probabilité est le bon. De toute évidence, la question statistique n’est pas la même que la question de probabilité, mais elles sont étroitement liées les unes aux autres. C’est pourquoi, une bonne introduction à la théorie statistique commencera par une discussion sur ce qu’est la probabilité et comment elle fonctionne.
7.2 Que signifie probabilité ?
Commençons par la première de ces questions. Qu’est-ce que la « probabilité » ? Cela peut vous surprendre, mais bien que les statisticiens et les mathématiciens s’entendent (pour la plupart) sur les règles de probabilité, il y a beaucoup moins de consensus sur ce que le mot signifie vraiment. Cela semble bizarre parce que nous sommes tous très à l’aise d’utiliser des mots comme « chance », « probable », « possible » et « probable », et il ne semble pas que ce soit une question à laquelle il devrait être très difficile de répondre. Mais si vous avez déjà vécu cette expérience dans la vie réelle, vous pourriez avoir l’impression de quitter la discussion en ayant le sentiment que vous ne l’avez pas bien comprise, et que (comme beaucoup de concepts courants) vous ne savez pas vraiment de quoi il s’agit.
Alors je vais essayer. Supposons que je veuille parier sur un match de football entre deux équipes de robots, Arduino Arsenal et C Milan. Après y avoir réfléchi, je décide qu’il y a 80% de chances qu’Arduino Arsenal gagne. Qu’est-ce que je veux dire par là ? Voici trois possibilité :
- Ce sont des équipes robotisées, donc je peux les faire jouer encore et encore, et si je le faisais, Arduino Arsenal gagnerait en moyenne 8 matchs sur 10.
- Pour n’importe quel jeu donné, je serais d’accord que parier sur ce jeu n’est « satisfaisant » que si un pari de $1 sur C Milan donne un gain de $5 (i.e. je reçois mon $1 plus un gain de $4 pour être juste), tout comme un pari de $4 sur Arduino Arsenal (i.e., mes $4 de mise plus une récompense de $1).
- Ma « croyance » subjective ou « confiance » en une victoire de l’Arduino Arsenal est quatre fois plus forte que ma croyance en une victoire du C Milan.
Chacune d’entre elles semble raisonnable. Cependant, ils ne sont pas identiques et les statisticiens ne les approuveraient pas tous. La raison à cela est qu’il existe différentes idéologies statistiques (oui, vraiment !) et selon celle dans laquelle vous souscrivez, vous pourriez dire que certaines de ces affirmations sont dénuées de sens ou non pertinentes. Dans cette section, je donne une brève introduction aux deux principales approches qui existent dans la littérature. Ce ne sont pas les seules approches, mais ce sont les deux plus importantes.
7.2.1 La vision fréquentiste
La première des deux grandes approches de la probabilité, et la plus dominante en statistique, est appelée le point de vue fréquentiste et elle définit la probabilité comme une fréquence récurrente. Supposons que nous essayions de jouer à pile ou face encore et encore. Par définition, il s’agit d’une pièce de monnaie qui a \(p\left( \text{face} \right) = 0,5\). Que pourrions-nous observer ? Une possibilité est que les 20 premiers lancers ressemblent à ceci :
P, F, F, F, F, P, P, F, F, F, F, P, F, F, P, P, P, P, P, F
Dans ce cas, 11 de ces 20 tours de pièces de monnaie (55 %) ont donné face. Supposons maintenant que j’ai compté le nombre de face (que j’appellerai NF) que j’ai vues, dans les N premiers lancers, et que je calcule à chaque fois la proportion de faces \({N_{F}}/{N}\). Voici ce que j’obtiendrais (j’ai vraiment fait pile ou face pour produire cela !) :

Notez qu’au début de la séquence, la proportion de faces fluctue énormément, à commencer par 0,00 et jusqu’à 0,80. Après, on a l’impression qu’elle diminue un peu, avec de plus en plus de valeurs qui se rapprochent de la « bonne » réponse de 0,50. C’est, en résumé, la définition fréquentiste de la probabilité. Tirez à pile ou face sur une pièce de monnaie et à mesure que N devient grand (s’approche de l’infini, noté \(N \rightarrow \infty\), la proportion de faces converge vers 50%. Les mathématiciens se soucient de certaines subtilités techniques, mais qualitativement parlant, c’est ainsi que les fréquentistes définissent la probabilité. Malheureusement, je n’ai pas un nombre infini de pièces de monnaie ou la patience infinie requise pour lancer une pièce de monnaie un nombre infini de fois. Cependant, j’ai un ordinateur et les ordinateurs excellent dans les tâches répétitives sans intelligence. J’ai donc demandé à mon ordinateur de simuler 1000 fois le lancer d’une pièce de monnaie, puis j’ai fait un graphique de ce qui arrive à la proportion de \({N_{f}}/{N}\) lorsque N augmente. En fait, je l’ai fait quatre fois juste pour m’assurer que ce n’était pas un hasard. Les résultats sont présentés à la Figure 7‑1. Comme vous pouvez le constater, la proportion de faces observées finit par cesser de fluctuer et se stabiliser. Lorsqu’elle le fait, le nombre auquel elle se stabilise finalement est la véritable probabilité des faces.
La définition fréquentiste de la probabilité présente certaines caractéristiques souhaitables. Premièrement, elle est objective. La probabilité d’un événement est nécessairement ancrée dans le monde. La seule façon dont les énoncés de probabilité peuvent avoir un sens, c’est lorsqu’ils font référence à des (une séquence d’) événements qui se produisent dans l’univers physique.40 Deuxièmement, elle est sans ambiguïté. Deux personnes qui regardent la même séquence d’événements se dérouler, en essayant de calculer la probabilité d’un événement, doivent inévitablement trouver la même réponse.
Cependant, elle a aussi des caractéristiques indésirables. Premièrement, les séquences infinies n’existent pas dans le monde physique. Supposons que vous avez pris une pièce dans votre poche et que vous avez commencé à la retourner. Chaque fois qu’elle atterrit, elle a un impact sur le sol. Chaque impact use un peu la pièce. La pièce finira par être détruite. On peut donc se demander s’il est vraiment sensé de prétendre qu’une séquence « infinie » de lancers de pièces de monnaie est même un concept ayant du sens ou objectif. Nous ne pouvons pas dire qu’une « séquence infinie » d’événements est une chose réelle dans l’univers physique, car l’univers physique ne permet rien d’infini. Plus sérieusement, la définition du fréquentiste a une vision étroite. Il y a beaucoup de choses auxquelles les êtres humains sont heureux d’attribuer des probabilités dans le langage courant, mais qui ne peuvent (même en théorie) être mises en correspondance avec une séquence hypothétique d’événements. Par exemple, si un météorologue vient à la télévision et dit « la probabilité de pluie à Adélaïde le 2 novembre 2048 est de 60% », nous sommes heureux de l’accepter. Mais on ne voit pas comment définir cela en termes fréquentistes. Il n’y a qu’une seule ville d’Adélaïde, et un seul le 2 novembre 2048. Il n’y a pas d’enchaînement infini d’événements ici, juste une chose unique. La probabilité fréquentiste nous interdit véritablement de faire des déclarations sur la probabilité d’un seul événement. Du point de vue fréquentiste, il pleuvra demain ou il ne pleuvra pas. Il n’y a pas de « probabilité » qui s’attache à un seul événement non répétable. Maintenant, il faut noter qu’il y a des astuces que les fréquentistes peuvent utiliser pour contourner ce problème. Il est possible que le météorologiste veuille dire quelque chose comme « Il y a une catégorie de jours pour lesquels je prévois une probabilité de 60 % de pluie, et si nous ne regardons que les jours pour lesquels je fais cette prédiction, alors, pour 60 % de ces jours, il pleuvra réellement ». C’est très bizarre et contre-intuitif de voir les choses de cette façon, mais on voit parfois des fréquentistes faire cela. Et il en sera question plus loin dans ce livre (voir section 8.5).
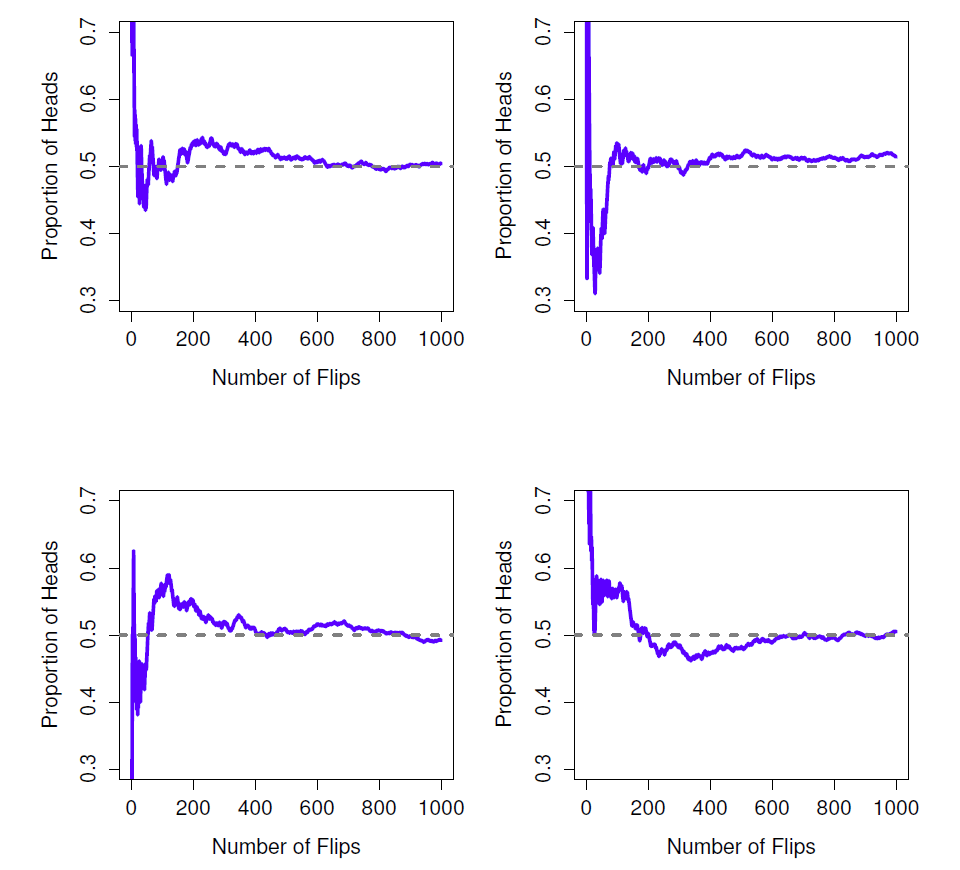
Figure 7‑1 : Une illustration du fonctionnement de la probabilité fréquentiste. Si vous tirez à pile ou face sur une pièce de monnaie, la proportion de faces (proportion of heads) que vous avez obtenues finit par diminuer et converge vers la probabilité réelle de 0,5. Chaque graphique présente quatre expériences simulées différentes. Dans chaque cas, nous faisons semblant d’avoir tiré à pile ou face 1000 fois et nous gardons une trace de la proportion de lancers (flips) qui tombait sur face au fur et à mesure que nous avancions. Bien qu’aucune de ces séquences n’ait atteint une valeur exacte de 0,5, si nous avions prolongé l’expérience pour un nombre infini de tours de pièces de monnaie, elles auraient pu le faire.
7.2.2 Le point de vue bayésienne
La vision bayésienne de la probabilité est souvent appelée la vision subjectiviste, et bien qu’elle ait été une vision minoritaire chez les statisticiens, elle n’a cessé de gagner du terrain au cours des dernières décennies. Il existe de nombreuses variante du bayésianisme, ce qui rend difficile de dire exactement ce qu’est « la » vision bayésienne. La façon la plus courante de penser la probabilité subjective est de définir la probabilité d’un événement comme le degré de croyance qu’un agent intelligent et rationnel attribue à cette vérité de cet événement. De ce point de vue, les probabilités n’existent pas dans le monde, mais plutôt dans les pensées et les hypothèses des gens et autres êtres intelligents.
Cependant, pour que cette approche fonctionne, nous avons besoin d’un moyen d’opérationnaliser le « degré de croyance ». Une façon de le faire est de le formaliser en termes de « paris rationnels », mais il existe de nombreuses autres façons. Supposons que je croie qu’il y a 60% de chances qu’il pleuve demain. Si quelqu’un me propose un pari selon lequel s’il pleut demain, je gagne 5 $, mais s’il ne pleut pas, je perds 5 $, de toute évidence, selon moi, c’est un assez bon pari. Par contre, si je pense que la probabilité de pluie n’est que de 40%, c’est un mauvais pari à prendre. Ainsi, nous pouvons opérationnaliser la notion de « probabilité subjective » en termes de ce que je suis prêt à accepter de parier.
Quels sont les avantages et les inconvénients de l’approche bayésienne ? L’avantage principal est qu’il vous permet d’assigner des probabilités à n’importe quel événement. Vous n’avez pas besoin d’être limité aux événements qui sont répétables. Le principal inconvénient (pour beaucoup de gens) est que nous ne pouvons pas être purement objectifs. Pour spécifier une probabilité, nous devons spécifier une entité qui a le degré de conviction pertinent. Cette entité peut être un humain, un extra-terrestre, un robot ou même un statisticien. Mais il doit y avoir un agent intelligent qui croit aux choses. Pour beaucoup de gens, c’est inconfortable, cela semble rendre la probabilité arbitraire. Alors que l’approche bayésienne exige que l’agent en question soit rationnel (c’est-à-dire qu’il obéisse aux règles des probabilités), elle permet à chacun d’avoir ses propres croyances. Je peux croire que la pièce est correcte et vous n’avez pas à le faire, même si nous sommes tous les deux rationnels. Le point de vue fréquentiste ne permet pas à deux observateurs d’attribuer des probabilités différentes à un même événement. Quand cela se produit, au moins l’un d’entre eux doit se tromper. Le point de vue bayésien n’empêche pas que cela se produise. Deux observateurs ayant des connaissances de base différentes peuvent légitimement avoir des croyances différentes sur le même événement. Bref, là où la vision fréquentiste est parfois jugée trop étroite (interdit beaucoup de choses auxquelles on veut attribuer des probabilités), la vision bayésienne est parfois jugée trop large (permet trop de différences entre observateurs).
7.2.3 Quelle est la différence ? Et qui a raison ?
Maintenant que vous avez examiné chacune de ces deux perspectives indépendamment, il est utile de vous garantir que vous pouvez comparer les deux. Revenez à l’hypothétique jeu de robots footballeurs au début de la section. Que pensez-vous qu’un fréquentiste et un Bayésien diraient de ces trois énoncés ? Selon un fréquentiste, quelle est la définition correcte de la probabilité ? Lequel choisirait un Bayésien ? Certaines de ces affirmations seraient-elles dénuées de sens pour un fréquentiste ou un Bayésien ? Si vous avez compris les deux points de vue, vous devriez avoir une idée de la façon de répondre à ces questions.
Bien, en supposant que vous compreniez la différence alors vous vous demandez peut-être lequel d’entre eux est vrai ? Honnêtement, je ne sais pas s’il y a une bonne réponse. Pour autant que je sache, il n’y a rien de mathématiquement incorrect dans la façon dont les fréquentistes pensent aux séquences d’événements, et il n’y a rien de mathématiquement incorrect dans la façon dont les Bayésiens définissent les croyances d’un agent rationnel. En fait, lorsque vous creusez dans les détails, les Bayésiens et les fréquentistes sont d’accord sur beaucoup de choses. De nombreuses méthodes fréquentistes conduisent à des décisions pour lesquelles les Bayésiens s’accordent à dire qu’un agent rationnel les prendrait. De nombreuses méthodes bayésiennes ont de très bonnes propriétés fréquentistes.
En général, je suis pragmatique, alors j’utiliserai n’importe quelle méthode statistique en laquelle j’ai confiance. Il s’avère que cela me fait préférer les méthodes bayésiennes pour des raisons que j’expliquerai vers la fin du livre. Mais je ne suis pas fondamentalement opposé aux méthodes fréquentistes. Tout le monde n’est pas aussi détendu. Prenons l’exemple de Sir Ronald Fisher, l’une des figures dominantes de la statistique du XXe siècle et un farouche opposant à tout ce qui est bayésien, dont l’article sur les fondements mathématiques des statistiques qualifiait la probabilité bayésienne de « jungle impénétrable [qui] arrête tout progrès vers la précision des concepts statistiques « (Fisher 1922b, p. 311). Ou le psychologue Paul Meehl, qui suggère que s’appuyer sur des méthodes fréquentistes pourrait faire de vous « un râteau intellectuel puissant mais stérile qui laisse dans son joyeux chemin un long train de jeunes filles violées mais pas de descendance scientifique viable » (Meehl (1967), p. 114). L’histoire des statistiques, comme vous pouvez le constater, n’est pas dénuée de divertissement.
En tout état de cause, si je préfère personnellement la vision bayésienne, la majorité des analyses statistiques sont basées sur l’approche fréquentiste. Mon raisonnement est pragmatique. Le but de ce livre est de couvrir à peu près le même territoire qu’une classe typique de statistiques de premier cycle en psychologie, et si vous voulez comprendre les outils statistiques utilisés par la plupart des psychologues, vous aurez besoin d’une bonne compréhension des méthodes fréquentistes. Je vous promets que ce n’est pas un effort inutile. Même si vous finissez par vouloir passer à la perspective bayésienne, vous devriez vraiment lire au moins un livre sur la vision fréquentiste « orthodoxe ». De plus, je n’ignorerai pas complètement la perspective bayésienne. De temps à autre, j’ajouterai quelques commentaires d’un point de vue bayésien, et je reviendrai sur le sujet plus en détail au chapitre 15.
7.3 Théorie de base des probabilités
En dépit des arguments idéologiques entre les Bayésiens et les fréquentistes, il s’avère que la plupart des gens s’entendent sur les règles auxquelles les probabilités doivent obéir. Il y a beaucoup de façons différentes d’en arriver à ces règles. L’approche la plus couramment utilisée est basée sur les travaux d’Andrey Kolmogorov, l’un des grands mathématiciens soviétiques du XXe siècle. Je n’entrerai pas dans les détails, mais je vais essayer de vous donner un petit aperçu de la façon dont cela fonctionne. Et pour ce faire, je vais devoir parler de mon pantalon.
7.3.1 Introduction des distributions de probabilités
Une des vérités troublantes de ma vie est que je ne possède que 5 pantalons. Trois jeans, la moitié inférieure d’un costume et un pantalon en survêtement. Encore plus triste, je leur ai donné des noms : Je les appelle X1, X2, X3, X4 et X5., C’est vraiment pour ça qu’on m’appelle M. Imaginatif. Maintenant, n’importe quel jour, je choisis exactement un pantalon à porter. Je ne suis pas assez stupide pour essayer de porter deux pantalons, et grâce à des années d’entraînement, je ne sors plus sans pantalon. Si je devais décrire cette situation en utilisant le langage de la théorie des probabilités, je dirais que chaque pantalon (c.-à-d. chaque X) est un événement élémentaire. La caractéristique clé des événements élémentaires est que chaque fois que nous faisons une observation (par exemple, chaque fois que je mets un pantalon), le résultat sera un et un seul de ces événements. Comme je l’ai dit, de nos jours, je porte toujours un seul pantalon pour que mes pantalons satisfassent à cette contrainte. De même, l’ensemble de tous les événements possibles s’appelle un l’espace d’échantillonnage. Certes, certains l’appelleraient une « garde-robe », mais c’est parce qu’ils refusent de penser à mon pantalon en termes probabilistes. C’est triste.
Ok, maintenant que nous avons un espace d’échantillonnage (une garde-robe), qui est construit à partir d’un grand nombre d’événements élémentaires possibles (pantalon), ce que nous voulons faire est d’assigner une probabilité à l’un de ces événements élémentaires. Pour un événement X, la probabilité de cet événement P(X) est un nombre compris entre 0 et 1 ; plus la valeur de P(X) est élevée, plus l’événement est probable. Ainsi, par exemple, P(X)=0 signifie que l’événement X est impossible (c’est-à-dire que je ne porte jamais ce pantalon). Par contre, si P(X)=1 signifie que l’événement X est certain (c’est-à-dire que je porte toujours ce pantalon). Pour les valeurs de probabilité au milieu, cela signifie que je porte parfois ce pantalon. Par exemple, si P(X)=0,5 signifie que je porte ce pantalon la moitié du temps.
A ce stade, on a presque fini. La dernière chose que nous devons reconnaître, c’est que « quelque chose arrive toujours ». Chaque fois que je mets un pantalon, je finis vraiment par porter un pantalon (c’est fou, non ?). Ce que cet énoncé quelque peu banal signifie, en termes probabilistes, c’est que les probabilités des événements élémentaires doivent être égales à 1, ce que l’on appelle la loi de la probabilité totale, sans que personne ne s’en soucie vraiment. Plus important encore, si ces exigences sont satisfaites, nous avons une distribution de probabilités. Par exemple, ceci est une distribution de probabilités :
| Quel pantalon ? | Étiquette | Probabilité |
| jeans bleu | X1 | \(P(X_{1}) = 0,5\) |
| Jeans gris | X2 | \(P(X_{1}) = 0,3\) |
| Jeans noir | X3 | \(P(X_{1}) = 0,1\) |
| Costume noir | X4 | \(P(X_{1}) = 0\) |
| Survêtement bleu | X5 | \(P(X_{1}) = 0,1\) |
Chacun des événements a une probabilité comprise entre 0 et 1, et si l’on additionne la probabilité de tous les événements, ils totalisent 1. Génial. Génial. On peut même dessiner un beau graphique à barres (voir section 5.3) pour visualiser cette distribution, comme le montre la Figure 7‑2. Et, à ce stade, nous avons tous accompli quelque chose. Vous avez appris ce qu’est une distribution de probabilité, et j’ai finalement réussi à trouver un moyen de créer un graphique qui se concentre entièrement sur mes pantalons. Tout le monde y gagne !
La seule autre chose que je dois souligner, c’est que la théorie des probabilités vous permet de parler d’événements non élémentaires aussi bien que d’événements élémentaires. La façon la plus simple d’illustrer le concept est d’utiliser un exemple. Dans l’exemple du pantalon, il est parfaitement légitime de parler de la probabilité que je porte un jean. Dans ce scénario, l’événement « Dan porte un jean » est censé s’être produit aussi longtemps que l’événement élémentaire qui s’est réellement produit est l’un des événements appropriés. Dans ce cas, « jeans bleu », « jeans noir » ou « jeans gris ». En termes mathématiques, nous avons défini l’événement E « jeans » pour correspondre à l’ensemble des événements élémentaires \((X_{1},X_{2},X_{3})\). Si l’un de ces événements élémentaires se produit alors E est également dit s’être produit. Après avoir décidé d’écrire la définition du E de cette façon, il est assez simple d’indiquer quelle est la probabilité P(E): on additionne tout. Dans ce cas particulier
\[ P\left( E \right) = P\left( X_{1} \right) + P\left( X_{2} \right) + P(X_{3}) \]
et, puisque les probabilités de jeans bleu, gris et noir sont respectivement 0,5 ; 0,3 et 0,1, la probabilité que je porte un jeans est égale à 0,9.
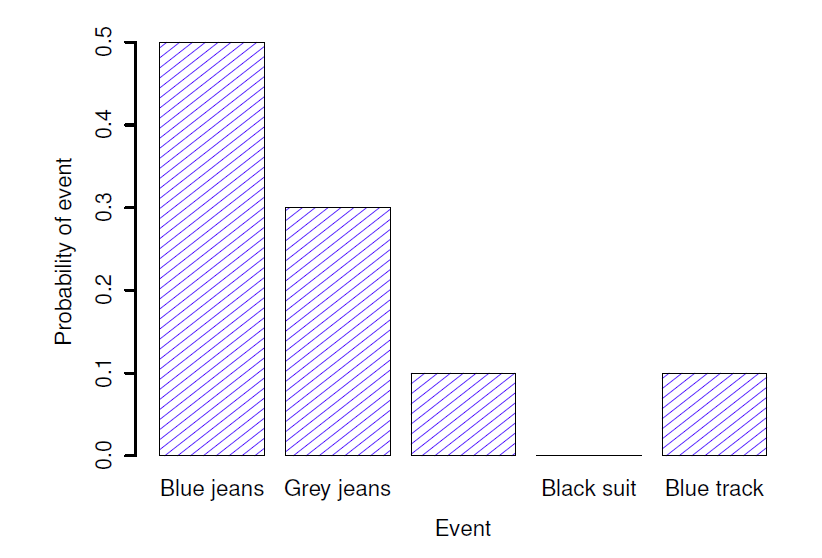
Figure 7‑2 : Représentation visuelle de la distribution de probabilité « pantalon ». Il y a cinq « événements élémentaires », correspondant aux cinq pantalons que je possède. Chaque événement a une certaine probabilité de se produire : cette probabilité est un nombre compris entre 0 et 1, la somme de ces probabilités étant égale à 1.
À ce stade, vous pensez peut-être que tout cela est terriblement évident et simple et vous auriez raison. Tout ce que nous avons vraiment fait, c’est d’envelopper quelques notions mathématiques de base autour de quelques intuitions de bon sens. Cependant, à partir de ces débuts simples, il est possible de construire des outils mathématiques extrêmement puissants. Je ne vais certainement pas entrer dans les détails de ce livre, mais ce que je vais faire, c’est énumérer, dans le Tableau 7‑1, certaines des autres règles que les probabilités satisfont. Ces règles peuvent être dérivées des hypothèses simples que j’ai décrites ci-dessus, mais comme nous n’utilisons pas ces règles pour quoi que ce soit dans ce livre, je ne le ferai pas ici.
Tableau 7‑1 : Quelques règles de base que les probabilités doivent satisfaire. Vous n’avez pas vraiment besoin de connaître ces règles pour comprendre les analyses dont nous parlerons plus loin dans le livre, mais elles sont importantes si vous voulez comprendre un peu plus profondément la théorie des probabilités.
| En français | Notation | Formule |
| Non A | \(P(\neg{A})\) | = \(1 - P(A)\) |
| A ou B | \(P(A\cup{B})\) | = \(P\left(A\right) + P\left(B\right) - P(A\cap{B})\) |
| A et B | \(P(A\cap{B})\) | = \(P\left(A|B\right)P(B)\) |
7.4 La distribution binomiale
Comme vous pouvez l’imaginer, les distributions de probabilités varient énormément et il existe une large gamme de distributions. Cependant, elles ne sont pas toutes d’égale importance. En fait, la grande majorité du contenu de ce livre repose sur l’une des cinq distributions suivantes : la distribution binomiale, la distribution normale, la distribution t, la distribution \(\chi^2\) (chi carré) et la distribution F. C’est pourquoi, au cours des prochaines sections, je vais vous présenter brièvement ces cinq distributions, en accordant une attention particulière à la binomiale et à la normale. Je vais commencer par la distribution binomiale puisque c’est la plus simple des cinq.
7.4.1 Présentation de la distribution binomiale
La théorie des probabilités est née de la tentative de décrire le fonctionnement des jeux de hasard ; il semble donc approprié que notre discussion sur la distribution binomiale comprenne une discussion sur les lancer de dés et de pièces à pile ou face. Imaginons une simple « expérience ». Dans ma petite main chanceuse, je tiens 20 dés identiques à six faces. Sur une face de chaque dé, il y a l’image d’un crâne, les cinq autres faces sont toutes vides. Si je lance les 20 dés, quelle est la probabilité que j’obtienne exactement 4 crânes ? En supposant que les dés sont corrects, nous savons que la probabilité qu’une personne meure en tirant le crâne est de 1 sur 6. En d’autres termes, la probabilité d’avoir un crâne pour un seul dé est d’environ 0,167. C’est assez d’information pour répondre à notre question, regardons comment cela se fait.
Comme d’habitude, nous allons vous présenter quelques noms et quelques notations. Nous laisserons N indiquer le nombre de jets de dés dans notre expérience, qui est souvent appelé paramètre de taille de notre distribution binomiale. Nous utiliserons aussi \(\theta\) pour faire référence à la probabilité qu’un seul dé présente un crâne, une quantité que l’on appelle habituellement la probabilité de succès de la binomiale.41 Enfin, nous utiliserons X pour faire référence aux résultats de notre expérience, à savoir le nombre de crânes que j’obtiens lorsque je lance les dés.
Tableau 7‑2 : Formules pour les distributions binomiale et normale. Nous n’utilisons pas vraiment ces formules pour quoi que ce soit dans ce livre, mais elles sont assez importantes pour un travail plus avancé, alors j’ai pensé qu’il serait peut-être préférable de les mettre ici dans un tableau, où elles ne peuvent pas gêner le texte. Dans l’équation de la distribution binomiale, X ! est la factorielle (c.-à-d. multiplier tous les nombres entiers de 1 à X), et pour la distribution normale, « exp » désigne la fonction exponentielle, dont nous avons parlé au chapitre 6. Si ces équations n’ont pas beaucoup de sens pour vous, ne vous en faites pas trop.
| Binomiale | \(P(X|\theta,N)=\frac{N!}{X!(N-X)!}\theta^{X}(1-\theta)^{N-X}\) |
| Normale | \(p(X|{\mu,\sigma})=\frac{1}{\sqrt{2\pi\sigma}}exp\left(-\frac{(X-\mu)^{2}}{2\sigma^{2}}\right)\) |
Puisque la valeur réelle de X est due au hasard, nous l’appelons variable aléatoire. Quoi qu’il en soit, maintenant que nous avons toute cette terminologie et cette notation, nous pouvons l’utiliser pour énoncer le problème un peu plus précisément. La quantité que l’on veut calculer est la probabilité que X = 4 étant donné que l’on sait que \(\theta=0,167\) et N=20. La « forme » générale de la chose que je veux calculer pourrait s’écrire comme suit :
\[ P\left( X \middle| \theta,N \right) \]
et nous nous intéressons au cas particulier où X = 4, \(\theta=0,167\) et N = 20. Il ne me reste plus qu’un seul élément de notation à mentionner avant de passer à la discussion sur la solution au problème. Si je veux dire que X est généré aléatoirement à partir d’une distribution binomiale avec les paramètres \(\theta\) et N, la notation que je devrais utiliser est la suivante :
\[ X \sim Binomiale(\theta,N) \]
Ouais, ouais !. Je sais ce que vous pensez : notation, notation, notation, notation. Vraiment, qui s’y intéresse ? Très peu de lecteurs de ce livre sont ici pour la notation, donc je devrais probablement passer à autre chose et parler de la façon d’utiliser la distribution binomiale. J’ai inclus la formule pour la distribution binomiale dans le Tableau 7‑2, puisque certains lecteurs voudront peut-être jouer avec, mais comme la plupart des gens ne s’en soucient probablement pas beaucoup et parce que nous n’avons pas besoin de la formule dans ce livre, je ne vais pas en parler en détail. Au lieu de cela, je veux juste vous montrer à quoi ressemble la distribution binomiale.
Pour cela, la Figure 7‑3 présente les probabilités binomiales pour toutes les valeurs possibles de X pour notre expérience de lancement de dés, de X = 0 (sans crânes) jusqu’à X = 20 (tous les crânes). Notez qu’il s’agit essentiellement d’un diagramme à barres qui n’est pas différent de celui que j’ai dessiné à la Figure 7‑2. Sur l’axe horizontal, nous avons tous les événements possibles, et sur l’axe vertical, nous pouvons lire la probabilité de chacun de ces événements. Ainsi, la probabilité d’obtenir 4 crânes sur 20 lancers est d’environ 0,20 (la réponse réelle est 0,2022036, comme nous allons le voir dans un instant). En d’autres termes, on s’attendrait à ce que cela se produise environ 20 % du temps où vous avez répété cette expérience.
Pour vous donner une idée de la façon dont la distribution binomiale change lorsque nous modifions les valeurs de \(\theta\) et N, supposons qu’au lieu de lancer des dés, je suis en train de lancer des pièces. Cette fois-ci, mon expérience consiste à lancer une pièce de monnaie à plusieurs reprises et le résultat qui m’intéresse est le nombre de faces que j’observe. Dans ce scénario, la probabilité de succès est maintenant \(\theta=1/2\).
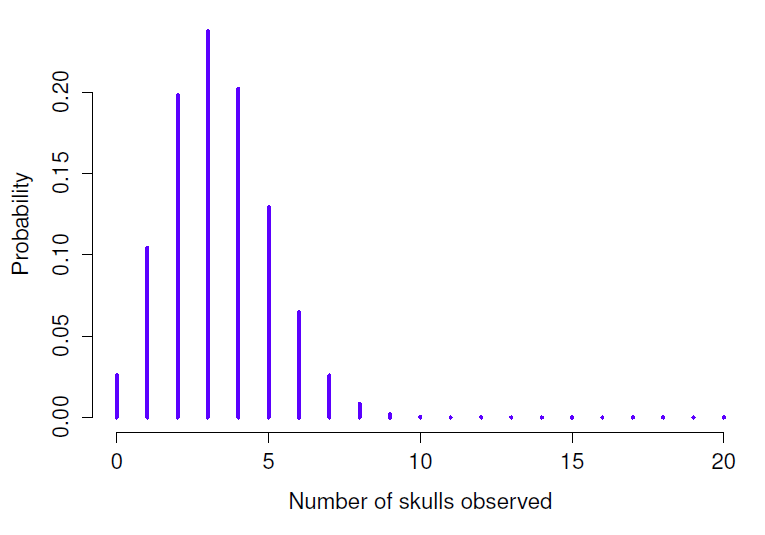
Figure 7‑3 : La distribution binomiale avec un paramètre de taille de N = 20 et une probabilité de succès sous-jacente de \(\theta= 1/6\) Chaque barre verticale représente la probabilité d’un résultat spécifique (c.-à-d. une valeur possible de X). Comme il s’agit d’une distribution de probabilités, chacune des probabilités doit être un nombre compris entre 0 et 1, et la somme des hauteurs des barres doit être égale à 1.
Supposons que je devais lancer la pièce N = 20 fois. Dans cet exemple, j’ai changé la probabilité de succès mais j’ai gardé la même taille d’expérience. Qu’est-ce que cela change à notre distribution binomiale ? Eh bien, comme le montre la Figure 7‑4a, l’effet principal est de déplacer toute la distribution, comme on peut s’y attendre. Bien, et si on jouait à pile ou face 100 fois ? Eh bien, dans ce cas, nous obtenons la Figure 7‑4b. La distribution reste à peu près au milieu, mais il y a un peu plus de variabilité dans les résultats possibles.
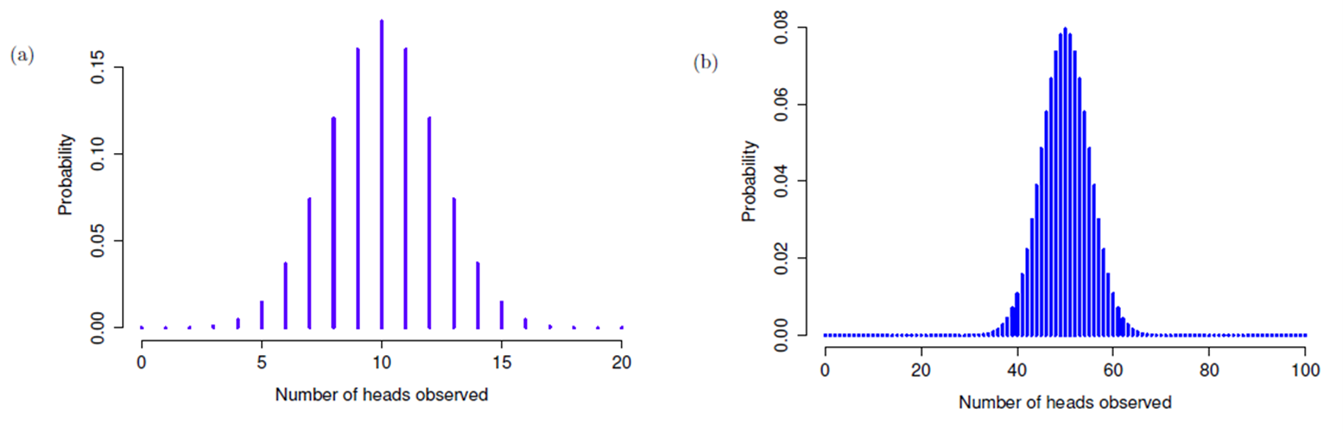
Figure 7‑4 : Deux distributions binomiales, impliquant un scénario dans lequel je tire à pile ou face, donc la probabilité de succès sous-jacente est \(\theta=1/2\). Dans le graphique (a), nous supposons que je lance la pièce N = 20 fois. Dans le panneau (b) nous supposons que la pièce est lancée N = 100 fois.
7.5 La distribution normale
Bien que la distribution binomiale soit conceptuellement la distribution la plus simple à comprendre, ce n’est pas la plus importante. Cet honneur particulier revient à la distribution normale, également appelée « courbe en cloche » ou « distribution gaussienne ». Une distribution normale est décrite à l’aide de deux paramètres : la moyenne de la distribution µ et l’écart-type de la distribution \(\sigma\).
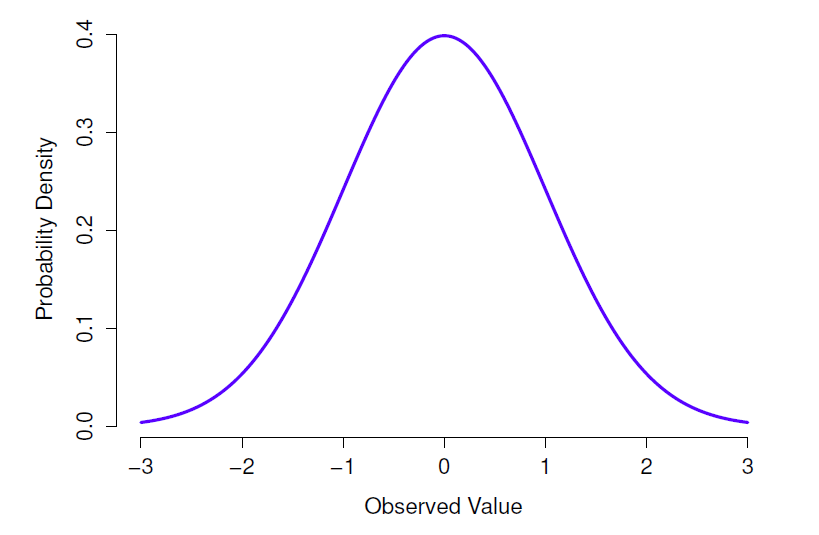
Figure 7‑5 : Distribution normale avec moyenne µ = 0 et écart-type\(\sigma=1\). L’axe des x correspond à la valeur d’une variable, et l’axe des y nous indique la probabilité d’observer cette valeur. Notez cependant que l’axe des y est appelé « densité de probabilités » et non « Probability ». Il y a une particularité subtile et quelque peu frustrante des distributions continues qui fait que l’axe des y se comporte un peu bizarrement : la hauteur de la courbe ici n’est pas vraiment la probabilité d’observer une valeur x particulière. D’autre part, il est vrai que les hauteurs de la courbe vous indiquent quelles valeurs x sont les plus probables (les plus élevées !) (voir section 7.5.1 pour tous les détails agaçants).
La notation que nous utilisons parfois pour dire qu’une variable X est normalement distribuée est la suivante :
\[ X \sim Normal(\mu,\sigma) \]
Bien sûr, c’est juste de la notation. Cela ne nous dit rien d’intéressant sur la distribution normale elle-même. Comme dans le cas de la distribution binomiale, j’ai inclus la formule de la distribution normale dans ce livre, parce que je pense qu’il est assez important que tous ceux qui apprennent les statistiques y jettent un coup d’œil, mais comme il s’agit d’un texte d’introduction, je ne veux pas m’y attarder, alors je l’ai mis de côté au Tableau 7‑2.
Au lieu de se concentrer sur les mathématiques, essayons de comprendre ce que signifie le fait qu’une variable soit normalement distribuée. Pour ce faire, jetez un coup d’œil à la Figure 7‑5 qui présente une distribution normale avec une moyenne µ = 0 et un écart-type \(\sigma = 1\). Vous pouvez voir d’où vient le nom « courbe en cloche » ; elle ressemble un peu à une cloche. Remarquez que, contrairement aux graphiques que j’ai dessinés pour illustrer la distribution binomiale, l’image de la distribution normale de la Figure 7‑5 montre une distribution lissée au lieu des barres d’un histogramme. Ce n’est pas un choix arbitraire, la distribution normale est continue alors que la distribution binomiale est discrète. Par exemple, dans l’exemple du jet de dé de la dernière section, il était possible d’obtenir 3 ou 4 crânes, mais impossible d’obtenir 3,9 crânes. Les chiffres que j’ai mentionnés dans la section précédente reflètent ce fait. Dans la Figure 7‑3, par exemple, il y a une barre située à X = 3 et une autre à ** = *4 mais il n’y a rien entre les deux. Les quantités continues n’ont pas cette contrainte. Supposons, par exemple, qu’il s’agisse du temps qu’il fait. La température par une agréable journée de printemps peut être de 23 degrés, 24 degrés, 23,9 degrés, ou n’importe quoi entre les deux, puisque la température est une variable continue. Par conséquent, une distribution normale pourrait être tout à fait appropriée pour décrire les températures printanières.42
En gardant cela à l’esprit, voyons si nous ne pouvons pas avoir une intuition sur le fonctionnement de la distribution normale. Voyons d’abord ce qui se passe quand on joue avec les paramètres de la distribution. Pour cela, la Figure 7‑6 présente les distributions normales qui ont des moyennes différentes mais ont le même écart-type.
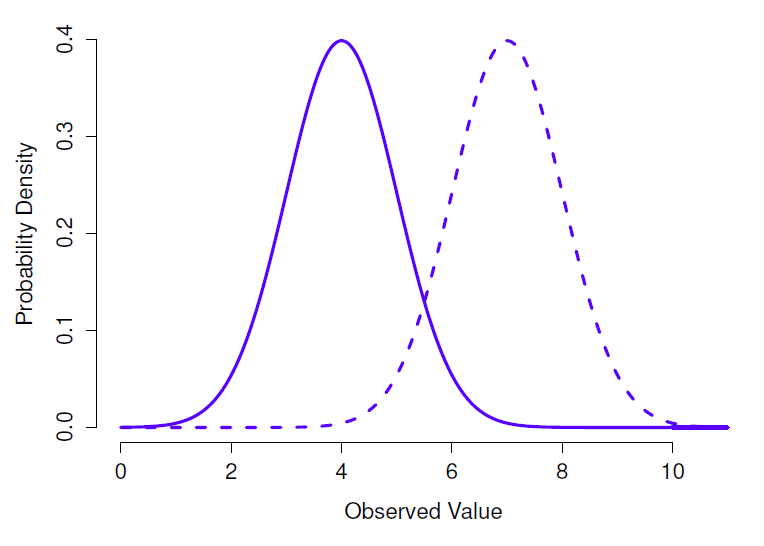
Figure 7‑6 : Une illustration de ce qui se passe lorsque vous modifiez la moyenne d’une distribution normale. Dans les deux cas, l’écart-type est \(\sigma=1\). Comme on pouvait s’y attendre, les deux distributions ont la même forme, mais la ligne en pointillés est décalée vers la droite.
Comme on peut s’y attendre, toutes ces distributions ont la même « largeur ». La seule différence entre eux est qu’ils ont été déplacés vers la gauche ou vers la droite. Sur tous les autres points, ils sont identiques. Par contre, si nous augmentons l’écart-type tout en maintenant la moyenne constante, le pic de la distribution reste au même endroit mais la distribution s’élargit, comme vous pouvez le voir à la Figure 7‑7. Notez, cependant, que lorsque nous élargissons la distribution, la hauteur du pic diminue.
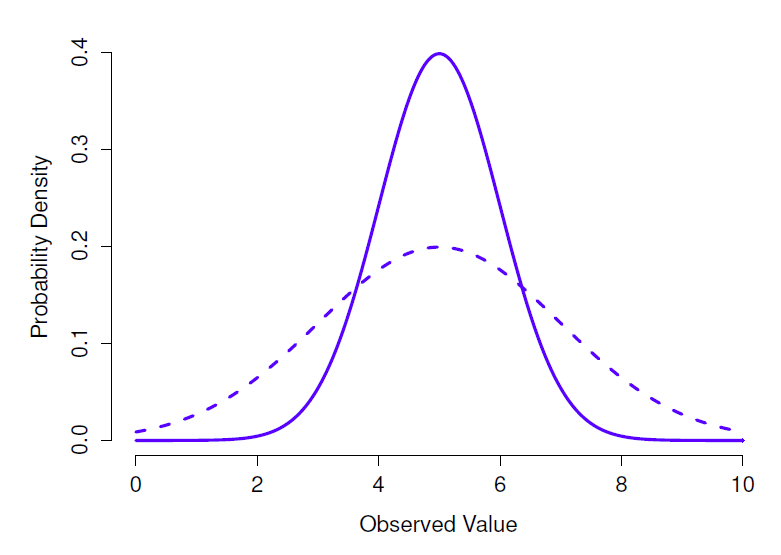
Figure 7‑7 : Une illustration de ce qui se passe lorsque vous modifiez l’écart-type d’une distribution normale. Les deux distributions représentées dans cette figure ont une moyenne de µ = 5, mais elles ont des écarts-types différents. La ligne pleine correspond à une distribution avec un écart-type \(\sigma=1\), et la ligne pointillée montre une distribution avec un écart-type \(\sigma=2\). Par conséquent, les deux distributions sont « centrées » au même endroit, mais la ligne pointillée est plus large que la solide.
Ceci doit se produire, de la même manière que les hauteurs des barres que nous avons utilisées pour dessiner une distribution binomiale discrète doivent totaliser 1, l’aire totale sous la courbe pour la distribution normale doit être égale à 1. Avant de poursuivre, j’aimerais souligner une caractéristique importante de la distribution normale. Indépendamment de la moyenne réelle et de l’écart-type, 68,3 % de la superficie se situe à moins d’un écart-type de la moyenne. De même, 95,4 % de la distribution se situe à l’intérieur de plus ou moins deux écarts-types de la moyenne et 99,7 % de la distribution se situe à l’intérieur de plus ou moins trois écarts-types. Cette idée est illustrée à la Figure 7‑8.
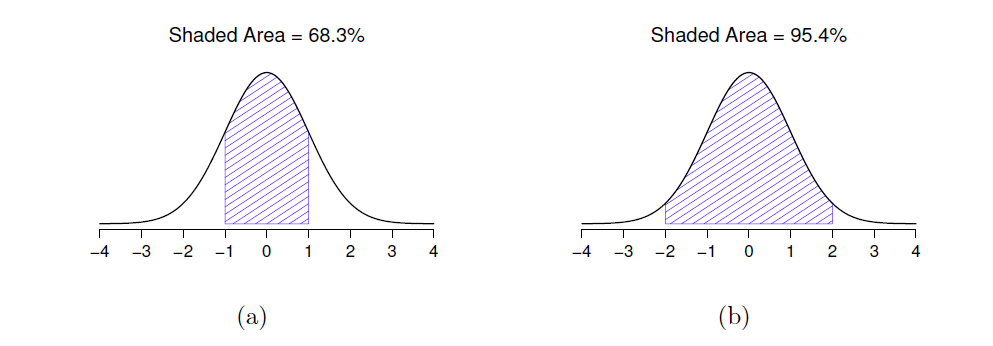
Figure 7‑8 : L’aire sous la courbe indique la probabilité qu’une observation se situe dans une plage particulière. Les lignes pleines représentent les distributions normales avec une moyenne µ = 0 et un écart-type \(\sigma=1\). Les zones ombrées illustrent les « zones sous la courbe » pour deux cas importants. Dans le panel a, nous pouvons voir qu’il y a 68,3 % de chances qu’une observation se situe dans un écart-type de la moyenne. Dans le panel b, nous voyons qu’il y a 95,4 % de chances qu’une observation se situe dans les deux écarts types de la moyenne.
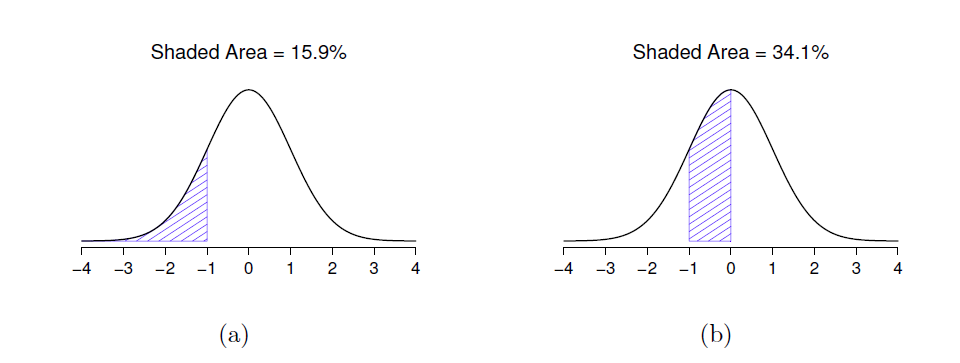
Figure 7‑9 : Deux autres exemples de « l’aire sous l’idée de courbe ». Il y a 15,9 % de chances qu’une observation se situe un écart-type inférieur ou supérieure à la moyenne (panel a), et 34,1 % de chances que l’observation se situe quelque part entre un écart-type inférieur à la moyenne et la moyenne (panel b). Notez que si vous additionnez ces deux chiffres, vous obtenez 15,9% + 34,1% = 50%. Pour les données normalement distribuées, il y a 50 % de chances qu’une observation soit inférieure à la moyenne. Et bien sûr, cela implique aussi qu’il y a 50 % de chances qu’elle soit supérieure à la moyenne.
7.5.1 Densité de probabilité
Il y a quelque chose que j’ai essayé de cacher tout au long de ma discussion sur la distribution normale, quelque chose que certains manuels d’introduction omettent complètement. Ils ont peut-être raison de le faire. Cette “chose” que je cache est bizarre et contre-intuitive, même si l’on s’en tient aux normes déformantes qui s’appliquent aux statistiques. Heureusement, ce n’est pas quelque chose que vous devez comprendre de manière approfondie pour faire des statistiques de base. C’est plutôt quelque chose qui commence à devenir important plus tard, quand vous aurez dépassé le stade de la base. Donc, si ça n’a pas de sens, ne vous inquiétez pas trop, mais assurez-vous d’en suivre l’essentiel.
Tout au long de ma discussion sur la distribution normale, il y a eu une ou deux choses qui ne se tiennent pas très bien. Vous avez peut-être remarqué que l’axe des y de ces figures est marqué « Densité de probabilité » plutôt que densité. Peut-être avez-vous remarqué que j’ai utilisé p(X) au lieu de P(X) lorsque j’ai donné la formule pour la distribution normale.
En fait, ce qui est présenté ici n’est pas vraiment une probabilité, c’est autre chose. Pour comprendre ce qu’est ce quelque chose, il faut passer un peu de temps à réfléchir à ce que signifie vraiment le fait de dire que X est une variable continue. Disons que nous parlons de la température extérieure. Le thermomètre me dit qu’il fait 23 degrés, mais je sais que ce n’est pas vraiment vrai. Il ne fait pas exactement 23 degrés. Il fait peut-être 23,1 degrés. Mais je sais que ce n’est pas vraiment vrai non plus parce qu’il pourrait faire 23,09 degrés. Mais je sais que… eh bien, vous avez compris l’idée. Ce qui est délicat avec les quantités réellement continues, c’est qu’on ne sait jamais vraiment ce qu’elles sont exactement.
Pensez maintenant à ce que cela implique lorsque nous parlons de probabilités. Supposons que la température maximale de demain soit échantillonnée à partir d’une distribution normale avec une moyenne de 23 et un écart-type 1. Quelle est la probabilité que la température atteigne exactement 23 degrés ? La réponse est « zéro », ou peut-être « un nombre si proche de zéro qu’il pourrait aussi bien être zéro ». Pourquoi en est-il ainsi ? C’est comme essayer de lancer une fléchette sur une cible infiniment petite. Peu importe à quel point vous visez bien, vous ne le toucherez jamais. Dans la vraie vie, vous n’obtiendrez jamais une valeur de 23 exactement. Ce sera toujours quelque chose comme 23,1 ou 22,99998 ou autre. En d’autres termes, il est tout à fait inutile de parler de la probabilité que la température soit exactement de 23 degrés. Cependant, dans le langage courant, si je vous disais qu’il faisait 23 degrés dehors et qu’il faisait 22,9998 degrés, vous ne me traiteriez probablement pas de menteur. Car dans le langage courant, « 23 degrés » veut dire en général quelque chose comme « entre 22,5 et 23,5 degrés ». Et bien qu’il ne semble pas avoir beaucoup de sens de s’interroger sur la probabilité que la température soit exactement de 23 degrés, il semble raisonnable de s’interroger sur la probabilité que la température se situe entre 22,5 et 23,5, ou entre 20 et 30, ou toute autre plage de températures.
Le but de cette discussion est de préciser que lorsqu’on parle de distributions continues, il n’est pas utile de parler de la probabilité d’une valeur précise. Cependant, ce dont nous pouvons parler, c’est de la probabilité que la valeur se situe à l’intérieur d’une fourchette particulière de valeurs. Pour connaître la probabilité associée à une plage particulière, il suffit de calculer « l’aire sous la courbe ». Nous avons déjà vu ce concept, dans la Figure 7‑8, les zones ombragées illustrent les probabilités réelles (p. ex. dans la Figure 7‑8a, elle montre la probabilité d’observer une valeur qui se situe à moins de 1 écart type de la moyenne).
Bien, donc cela explique une partie de l’histoire. J’ai expliqué un peu comment les distributions de probabilités continues devraient être interprétées (c’est-à-dire que l’aire sous la courbe est l’élément clé). Mais que signifie la formule pour p(x) que j’ai décrite plus tôt ? Évidemment, p(x) ne décrit pas une probabilité, mais qu’est-ce que c’est ? Le nom de cette quantité p(x) est une densité de probabilité, et dans les graphiques que nous avons dessinés, elle correspond à la hauteur de la courbe. Les densités elles-mêmes ne sont pas significatives en soi, mais elles sont « arrangées » pour s’assurer que l’aire sous la courbe puissent toujours être interprétée comme de véritables probabilités. Pour être honnête, c’est à peu près tout ce que vous avez vraiment besoin de savoir pour l’instant.43
7.6 Autres distributions utiles
La distribution normale est la distribution la plus utilisée par les statistiques (pour des raisons qui seront discutées sous peu), et la distribution binomiale est très utile à de nombreuses fins. Mais le monde des statistiques est rempli de distributions de probabilités, dont certaines que nous rencontrerons en passant. En particulier, les trois qui apparaîtront dans ce livre sont la distribution t, la distribution \(\chi^{2}\) et la distribution F. Je ne donnerai pas de formules pour aucune d’entre elles, ni n’en parlerai trop en détail, mais je vais vous montrer quelques images.
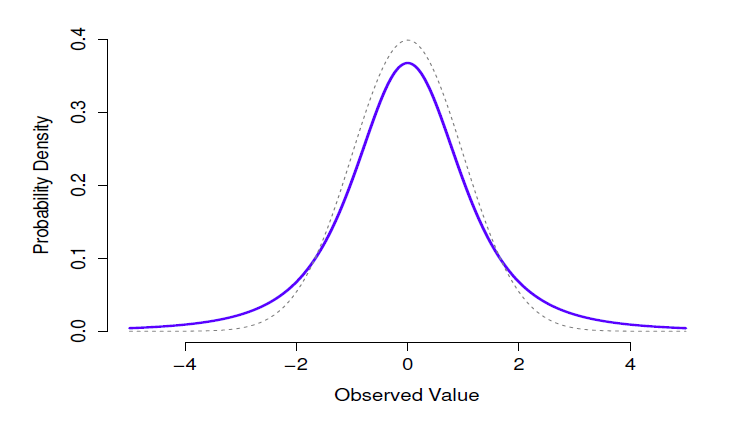
Figure 7‑10 : Distribution t avec 3 degrés de liberté (ligne pleine). Cela ressemble à une distribution normale, mais ce n’est pas tout à fait la même chose. À des fins de comparaison, j’ai tracé une distribution normale standard sous la forme d’une ligne pointillée.
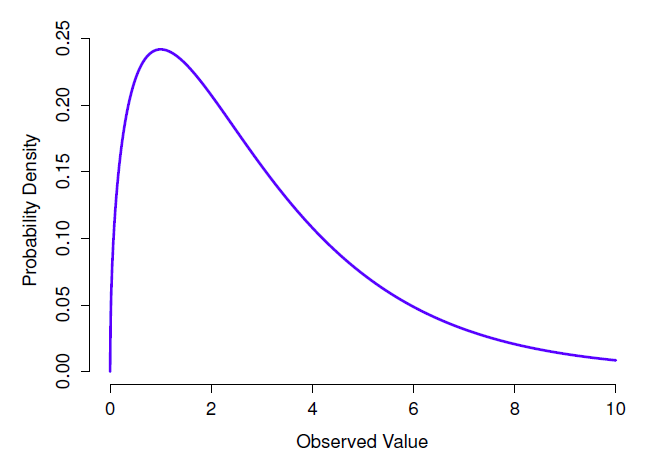
Figure 7‑11 : Une distribution \(\chi^{2}\) avec 3 degrés de liberté. Notez que les valeurs observées doivent toujours être supérieures à zéro et que la distribution est assez asymétrique. Ce sont les principales caractéristiques d’une distribution du chi carré
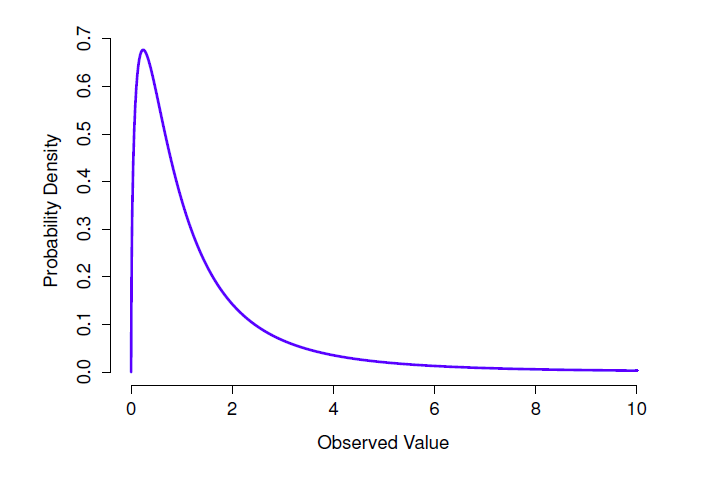
Figure 7‑12 : Une distribution F avec 3 et 5 degrés de liberté. Qualitativement parlant, cela ressemble beaucoup à une distribution du chi carré, mais ce n’est pas tout à fait la même chose
- La distribution t est une distribution continue qui ressemble beaucoup à une distribution normale, voir Figure 7‑10. Notez que les « queues » de la distribution t sont « plus lourdes » (c’est-à-dire qu’elles s’étendent plus vers l’extérieur) que les queues de la distribution normale). C’est la différence importante entre les deux. Cette distribution tend à se produire dans les situations où vous pensez que les données suivent une distribution normale, mais que vous ne connaissez pas la moyenne ou l’écart-type. Nous reviendrons sur cette distribution au chapitre 11.
- La distribution \(\chi^{2}\) est une autre distribution qui apparaît dans beaucoup d’endroits différents. La situation dans laquelle nous le verrons est celle de l’analyse des données catégoriques (chapitre 10), mais c’est l’une de ces choses qu’on rencontre un peu partout en fait. Quand vous creusez dans les mathématiques (et qui n’aime pas faire cela ?), il s’avère que la principale raison pour laquelle la distribution \(\chi^{2}\) apparaît partout est que si vous avez plusieurs variables qui sont normalement distribuées, que vous calculez le carré leurs valeurs et puis les additionner (une procédure appelée « faire la somme des carrés »), cette somme a une distribution \(\chi^{2}\). Vous seriez étonné de voir combien de fois ce fait s’avère utile. Quoi qu’il en soit, voici à quoi ressemble une distribution de \(\chi^{2}\) : Figure 7‑11.
- La distribution F ressemble un peu à une distribution \(\chi^{2}\), et elle apparaît chaque fois que vous avez besoin de comparer deux distributions \(\chi^{2}\) entre elles. Certes, cela ne semble pas exactement quelque chose que toute personne saine d’esprit voudrait faire, mais cela s’avère très important dans l’analyse des données du monde réel. Rappelez-vous quand j’ai dit que \(\chi^{2}\) s’avère être la distribution clé quand on prend une « somme de carrés » ? Eh bien, ce que cela signifie, c’est que si vous voulez comparer deux « sommes de carrés » différents, vous parlez probablement de quelque chose qui a une distribution F. Bien sûr, je ne vous ai pas encore donné d’exemple de quelque chose qui implique une somme de carrés, mais je le ferai au chapitre 13. Et c’est là qu’on tombera sur la distribution F. Oh, et il y a une image à la Figure 7‑12.
Bien, il est temps de terminer cette section. Nous avons vu trois nouvelles distributions : \(\chi^{2}\), t et F. Ce sont toutes des distributions continues, et elles sont toutes étroitement liées à la distribution normale. L’essentiel pour nous, c’est que vous saisissiez l’idée de base que ces distributions sont toutes profondément liées les unes aux autres, et à la distribution normale. Plus loin dans ce livre, nous allons rencontrer des données qui sont normalement distribuées, ou du moins supposées l’être. Ce que je veux que vous compreniez maintenant, c’est que, si vous supposez que vos données sont normalement distribuées, vous ne devriez pas être surpris de voir les distributions \(\chi^{2}\), t et F apparaître partout quand vous commencez à essayer de faire votre analyse de données.
7.7 Résumé
Dans ce chapitre, nous avons parlé de probabilité. Nous avons parlé de ce que la probabilité signifie et pourquoi les statisticiens ne s’entendent pas sur ce qu’elle signifie. Nous avons parlé des règles auxquelles les probabilités doivent obéir. Et nous avons introduit l’idée d’une distribution de probabilités et passé une bonne partie du chapitre à parler de certaines des distributions de probabilités les plus importantes avec lesquelles les statisticiens travaillent. La ventilation section par section ressemble à ceci :
- Théorie des probabilités et statistiques (section 7.1)
- Opinions fréquentistes et bayésiennes sur la probabilité (section 7.2)
- Notions de base de la théorie des probabilités (section 7.3)
- Distribution binomiale (section 7.4), distribution normale (section 7.5) et autres (section 7.6)
Comme vous pouvez vous y attendre, ce panorama n’est en aucun cas exhaustif. La théorie des probabilités est une importante branche des mathématiques à part entière, entièrement distincte de son application aux statistiques et à l’analyse des données. Ainsi, il existe des milliers de livres écrits sur le sujet et les universités offrent généralement de multiples cours entièrement consacrés à la théorie des probabilités. Même la tâche « plus simple » de documenter les distributions de probabilités standard est un grand sujet. J’ai décrit cinq distributions de probabilités standard dans ce chapitre, mais j’ai un livre de 45 chapitres intitulé « Statistical Distributions » (Evans, Barston, and Pollard 1983) qui contient beaucoup plus que cela. Heureusement pour vous, très peu sont nécessaires. Il est peu probable que vous ayez besoin de connaître des douzaines de distributions statistiques lorsque vous effectuez des analyses de données dans le monde réel, et vous n’en aurez certainement pas besoin pour ce livre, mais cela ne fait jamais de mal de savoir qu’il y a d’autres possibilités.
Pour en revenir à ce dernier point, on a l’impression que tout ce chapitre n’est qu’une digression. Beaucoup d’étudiants des cours de psychologie de premier cycle en statistique lisent ce contenu très rapidement (je sais que le mien l’a fait), et même les cours les plus avancés « oublient » souvent de revoir les fondements fondamentaux du domaine. La plupart des psychologues universitaires ne connaîtraient pas la différence entre la probabilité et la densité et, jusqu’à tout récemment, très peu d’entre eux étaient au courant de la différence entre la probabilité bayésienne et la probabilité fréquentiste. Cependant, je pense qu’il est important de comprendre ces choses avant de passer aux applications. Par exemple, il y a beaucoup de règles sur ce que vous êtes « autorisé » à dire lorsque vous faites des inférences statistiques et beaucoup d’entre elles peuvent sembler arbitraires et étranges. Cependant, elles commencent à avoir du sens si vous comprenez qu’il y a cette distinction bayésienne/fréquentiste. De même, au chapitre 11, nous allons parler de ce qu’on appelle le t-test, et si vous voulez vraiment avoir une idée de la mécanique du t-test, il est vraiment utile d’avoir une idée de ce à quoi ressemble réellement une distribution t. Vous comprenez l’idée, j’espère.
References
Evans, J. St. B. T., Julie L. Barston, and Paul Pollard. 1983. “On the Conflict Between Logic and Belief in Syllogistic Reasoning.” Memory & Cognition 11 (3): 295–306. https://doi.org/10.3758/BF03196976.
Meehl, Paul E. 1967. “Theory-Testing in Psychology and Physics: A Methodological Paradox.” Philosophy of Science 34 (2): 103–15.
Cela ne veut pas dire que les fréquentistes ne peuvent pas faire des affirmations hypothétiques, bien sûr. C’est simplement que si vous voulez faire une affirmation sur la probabilité, il doit être possible de la redécrire en termes d’une séquence d’événements potentiellement observables, avec les fréquences relatives des différents résultats qui apparaissent dans cette séquence.↩︎
Notez que le terme “succès” est plutôt arbitraire et n’implique pas que le résultat est quelque chose à désirer. Si \(\theta\) faisait référence à la probabilité qu’un passager se blesse dans un accident d’autobus, j’appellerais cela la probabilité de succès, mais cela ne veut pas dire que je veux que les gens soient blessés dans un accident d’autobus !↩︎
En pratique, la distribution normale est si pratique que les gens ont tendance à l’utiliser même lorsque la variable n’est pas réellement continue. Tant qu’il y a suffisamment de catégories (p. ex. réponses à un questionnaire selon l’échelle de Likert), il est assez courant d’utiliser la distribution normale comme approximation. Cela fonctionne beaucoup mieux en pratique que vous ne le pensez.↩︎
Pour les lecteurs qui connaissent un peu le calcul, je vais donner une explication un peu plus précise. De la même manière que les probabilités sont des nombres non négatifs qui doivent s’additionner à 1, les densités de probabilité sont des nombres non négatifs qui doivent s’intégrer à 1 (où l’intégrale est prise sur toutes les valeurs possibles de X). Pour calculer la probabilité que X se situe entre a et b, nous calculons l’intégrale définie de la fonction de densité sur la plage correspondante, \(\int_{a}^{b}{p\left( x \right)\text{dx}}\).Si vous ne vous souvenez pas ou si vous n’avez jamais appris le calcul, ne vous en faites pas. Ce n’est pas nécessaire pour ce livre.↩︎