Chapitre 6 Problèmes pratiques
Le jardin de la vie ne semble jamais se limiter aux intrigues que les philosophes ont tracées pour son confort. Peut-être que quelques tracteurs de plus feraient l’affaire. - Roger Zelazny32
C’est un chapitre un peu étrange, même selon mes critères. Mon objectif dans ce chapitre est de parler un peu plus honnêtement des réalités du travail avec les données que vous ne le verrez ailleurs dans le livre. Le problème avec les ensembles de données du monde réel, c’est qu’ils sont désordonnés. Très souvent, le fichier de données avec lequel vous commencez n’a pas les variables stockées dans le bon format pour l’analyse que vous voulez faire. Parfois, il peut y avoir beaucoup de valeurs manquantes dans votre ensemble de données. Parfois, vous ne voulez analyser qu’un sous-ensemble des données. Et cetera. En d’autres termes, il y a beaucoup de manipulation de données que vous devez faire juste pour obtenir les variables dans votre ensemble de données dans le format dont vous avez besoin. Le but de ce chapitre est de fournir une introduction de base à ces sujets pragmatiques. Bien que le chapitre soit motivé par le genre de problèmes pratiques qui surgissent lors de la manipulation de données réelles, je m’en tiendrai à la pratique que j’ai adoptée dans la majeure partie du livre et je m’appuierai sur de très petits ensembles de données qui illustrent le problème sous-jacent. Comme ce chapitre est essentiellement un recueil de techniques et qu’il ne raconte pas une seule histoire cohérente, il peut être utile de commencer par une liste de sujets :
- Section 6.1. Mise en tableaux des données.
- Section 6.2. Utiliser des expressions logiques.
- Section 6.3. Transformer ou recoder une variable.
- Section 6.4. Quelques fonctions mathématiques utiles.
- Section 6.5. Extraction d’un sous-ensemble d’un ensemble de données.
Comme vous pouvez le constater, la liste des sujets abordés dans le chapitre est assez vaste, et il y a beaucoup de contenu. Même s’il s’agit d’un des chapitres les plus longs et les plus difficiles du livre, je ne fais qu’effleurer plusieurs sujets assez différents et importants. Mon conseil, comme d’habitude, est de lire le chapitre une fois et d’essayer de le suivre autant que possible. Ne vous inquiétez pas trop si vous ne pouvez pas tout saisir d’un coup, surtout dans les sections suivantes. Le reste du livre ne s’appuie que légèrement sur ce chapitre pour que vous puissiez vous en sortir avec une simple compréhension des bases. Cependant, ce que vous découvrirez probablement plus tard, c’est que vous devrez revenir à ce chapitre pour comprendre certains des concepts auxquels je fais référence ici.
6.1 Mise en tableaux et recoupement des données
Une tâche très courante lors de l’analyse des données est la construction de tableaux de fréquence, ou de tableaux croisés d’une variable par rapport à une autre. Ces tâches peuvent être réalisées avec Jamovi et je vais vous montrer comment dans cette section.
6.1.1 Création de tables pour des variables individuelles
Commençons par un exemple simple. En tant que père d’un petit enfant, je passe naturellement beaucoup de temps à regarder des émissions de télévision comme In the Night Garden. Dans le fichier nightgarden.csv, j’ai transcrit une courte section du dialogue. Le fichier contient deux variables d’intérêt, le locuteur (speaker) et l’énoncé (Utterance). Ouvrez cet ensemble de données dans Jamovi et jetez un coup d’œil aux données dans la vue « feuille de calcul ». Vous verrez que les données ressemblent à ceci :
Variable « Speaker » :
upsy-daisy upsy-daisy upsy-daisy upsy-daisy upsy-daisy tombliboo tombliboo makka-pakka makka-pakka makka-pakka makka-pakka makka-pakka makka-pakka
variable « Utterance » :
pip pip pip onk onk onk ee oo pip pip onk onk onk
En regardant cela apparait clairement ce qui est arrivé à ma santé mentale ! Avec des données comme celle-ci, une tâche à laquelle je pourrais me trouver confronter est de construire un compte de fréquence du nombre de mots que chaque personnage parle pendant l’émission. Le menu Jamovi « Descriptives » comporte une case à cocher appelée « Frequencies Tables» qui fait cela, voir Figure 6‑1.
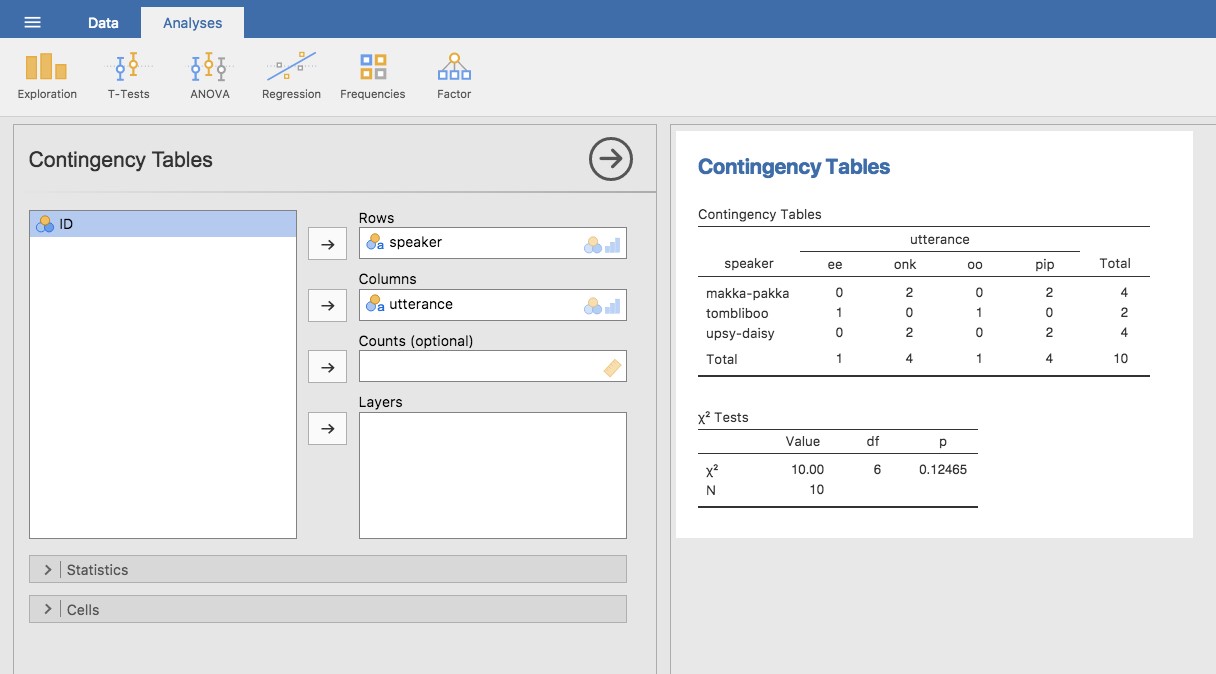
Figure 6‑2 : Tableau de contingence pour le locuteur et les variables des énoncés
Ne vous inquiétez pas pour le tableau « \(\chi^{2}\) Tests » qui est produit. Nous reviendrons sur ce point plus loin au chapitre 10. Lors de l’interprétation du tableau de contingence, n’oubliez pas qu’il s’agit de comptages, de sorte que le fait que la première ligne et la deuxième colonne de chiffres correspondent à une valeur de 2 indique que Makka-Pakka (ligne 1) a dit « onk » (colonne 2) deux fois dans cet ensemble de données.
6.1.2 Ajout de pourcentages à un tableau de contingence
Le tableau de contingence illustré à la Figure 6‑2 présente un tableau des fréquences brutes. C’est-à-dire, un compte du nombre total de cas pour différentes combinaisons de niveaux des variables spécifiées. Cependant, vous voulez souvent que vos données soient organisées en termes de pourcentages aussi bien que de comptages. Vous pouvez trouver les cases à cocher pour différents pourcentages sous l’option « Cellules » dans la fenêtre « Tableaux de contingence ». Tout d’abord, cliquez sur la case à cocher « Ligne » et le tableau de contingence dans la fenêtre de sortie deviendra celui de la Figure 6‑3.
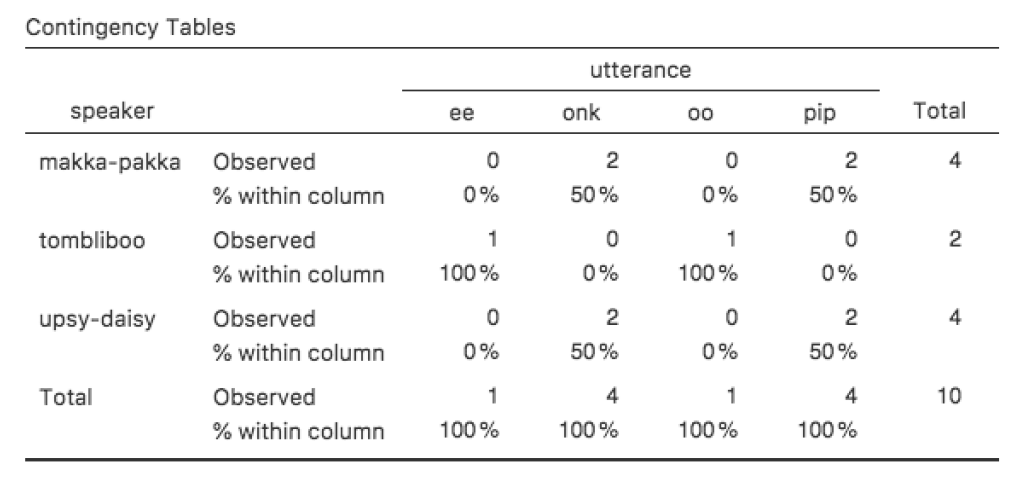
Figure 6‑4 : Tableau de contingence pour le speaker et le variable Utterrance, avec les pourcentages en colonnes
Dans cette version, ce que nous voyons est le pourcentage de caractères associés à chaque énoncé. Par exemple, chaque fois que l’énoncé « ee » est prononcé (dans cet ensemble de données), 100% du temps c’est un Tombliboo qui le dit.
6.2 Expressions logiques dans Jamovi
Un concept clé sur lequel s’appuient beaucoup de transformations de données dans Jamovi est l’idée d’une valeur logique. Une valeur logique est une affirmation sur le fait que quelque chose est vrai ou faux. Ceci est implémenté dans Jamovi d’une manière assez simple. Il y a deux valeurs logiques, à savoir VRAI et FAUX. Malgré leur simplicité, les valeurs logiques sont très utiles. Voyons comment ils fonctionnent.
6.2.1 Évaluer les vérités mathématiques
Dans le livre classique de George Orwell de 1984, l’un des slogans utilisés par le Parti totalitaire était « deux plus deux égalent cinq ». L’idée étant que la domination politique de la liberté humaine devient complète lorsqu’il est possible de renverser même la vérité la plus fondamentale. C’est une pensée terrifiante, surtout quand le protagoniste Winston Smith s’effondre finalement sous la torture et accepte la proposition. « L’homme est infiniment malléable », dit le livre. Je suis presque sûr que ce n’est pas vrai pour les humains33 et ce n’est certainement pas vrai pour Jamovi. Jamovi n’est pas infiniment malléable, il a des opinions plutôt fermes à propos de ce qui est et n’est pas vrai, du moins en mathématiques de base. Si je lui demande de calculer 2 + 234, il donne toujours la même réponse, et ce n’est pas 5 !
Bien sûr, pour l’instant, Jamovi ne fait que les calculs. Je ne lui ai pas demandé d’affirmer explicitement que 2 + 2 = 4 est une vraie affirmation. Si je veux que Jamovi fasse un jugement explicite, je peux utiliser une commande comme celle-ci : 2 + 2 == 4
Ce que j’ai fait ici est d’utiliser l’opérateur d’égalité, ==, pour forcer Jamovi à faire un jugement «vrai ou faux».[Notez qu’il s’agit d’un opérateur très différent de l’opérateur égal =. Une coquille commune que les gens font lorsqu’ils essaient d’écrire des commandes logiques en Jamovi (ou dans d’autres langues, puisque la distinction “= versus ==” est importante dans de nombreux programmes informatiques et statistiques) est de saisir accidentellement = quand vous voulez vraiment dire ==. Soyez particulièrement prudent avec cela, je programme dans plusieurs langues depuis mon adolescence et je foire encore beaucoup cela. Hmm. Je crois comprendre pourquoi je n’étais pas cool quand j’étais ado. Et pourquoi je ne suis toujours pas cool.] Bien, voyons ce que Jamovi pense du slogan du Parti, alors tapez ceci dans la boîte de calcul de la nouvelle variable « Formula » :
2 + 2 == 5
Qu’obtenez-vous ? Il devrait s’agir d’un ensemble complet de valeurs « FALSE » dans la colonne de la feuille de calcul pour votre variable nouvellement calculée. Youpi ! Liberté et poneys pour tous ! Ou quelque chose comme ça.
Quoi qu’il en soit, ça valait la peine de jeter un coup d’œil sur ce qui se passe si j’essaie de forcer Jamovi à croire que deux plus deux font cinq en écrivant une formule comme 2 + 2 = 5. Je sais que si je fais cela dans un autre programme, par exemple R, alors il affiche un message d’erreur. Mais attendez, si vous faites cela en Jamovi, vous obtenez tout un ensemble de valeurs « FALSE » valeurs. Alors, que se passe-t-il ? Eh bien, il semble que Jamovi est assez intelligent et réalise que vous testez si c’est VRAI ou FAUX que 2 + 2 = 5, peu importe si vous utilisez le bon opérateur d’égalité, ==, ou le signe égal =.
6.2.2 Opérations logiques
Bien maintenant, nous avons vu des opérations logiques à l’œuvre. Mais jusqu’à présent, nous n’avons vu que l’exemple le plus simple possible. Vous ne serez probablement pas surpris de découvrir que nous pouvons combiner des opérations logiques avec d’autres opérations et fonctions d’une manière plus complexe, comme celle-ci :
3*3 + 4*4 == 5*5
ou ceci
SQRT(25) == 5
Non seulement cela, mais comme l’illustre le Tableau 6‑1, il existe plusieurs autres opérateurs logiques que vous pouvez utiliser correspondant à certains concepts mathématiques de base. J’espère que tous ceux-ci se comprennent d’eux-mêmes. Par exemple, le l’opérateur moins que < vérifie si le nombre à gauche est inférieur au nombre à droite. Si c’est moins, alors Jamovi retourne une réponse VRAI, mais si les deux nombres sont égaux, ou si celui de droite est plus grand, alors Jamovi retourne une réponse FAUX.
En revanche, l’opérateur inférieur ou égal à <= fera exactement ce qu’il dit. Elle retourne une valeur de VRAI si le numéro du côté gauche est inférieur ou égal au numéro du côté droit. A ce stade, j’espère que ce que font les opérateurs plus grand que > et plus grand ou égal que >= est assez évident.
Dans la liste des opérateurs logiques est l’opérateur pas égal à != comme avec tous les autres, fait ce qu’il dit qu’il fait. Il retourne une valeur de VRAI lorsque les choses ne sont pas identiques de part et d’autre. Par conséquent, puisque 2 + 2 n’est pas égal à 5, nous obtiendrions VRAI comme valeur pour notre variable nouvellement calculée. Essayez et vous verrez :
2 + 2! = 5
Nous n’avons pas encore tout à fait fini. Il y a trois autres opérations logiques énumérées dans le Tableau 6‑2 qu’il vaut la peine de connaître. Ce sont les opérateurs non ! , opérateur et and, et l’opérateur ou or. Comme les autres opérateurs logiques, leur comportement est plus ou moins exactement ce à quoi on pourrait s’attendre étant donné leur nom.
Tableau 6‑1 : Quelques opérateurs logiques. Techniquement, je devrais les appeler « opérateurs relationnels binaires », mais franchement, je n’en ai pas envie. C’est mon livre donc que personne ne m’y oblige.
| Operation | operateur | exemple d’entrée | Résultats |
| moins de | < | 2 < 3 | VRAI |
| inférieur ou égal à | <= | 2 <= 2 | VRAI |
| supérieur à | > | 2 > 3 | FAUX |
| supérieur ou égal à | >= | 2 >= 2 | VRAI |
| égal à | == | 2 == 3 | FAUX |
| n’est pas égal à | != | 2 != 3 | VRAI |
Tableau 6‑2 : Quelques opérateurs plus logiques
| Opération | Opérateur | exemple d’entrée | Résultats |
| ne pas | NON | NOT(1==1) | FAUX |
| ou | ou | (1==1) or (2==3) | VRAI |
| et | et | (1==1) and (2==3) | FAUX |
Par exemple, si je vous demande d’évaluer l’affirmation selon laquelle « 2 + 2 = 4 ou 2+ 2 = 5 » vous verrez que c’est vrai. Puisqu’il s’agit d’une alternative où on a « soit l’un, soit l’autre », tout ce dont nous avons besoin, c’est que l’un des deux termes soit vrai. C’est ce que fait l’opérateur or :35
(2+2 == 4) or (2+2 == 5)
Par contre, si je vous demande d’évaluer l’affirmation selon laquelle « 2 - 2 = 4 et 2 - 2 = 2 = 5 », vous diriez que c’est faux. Puisqu’il s’agit d’une conjonction, nous avons besoin que les deux parties soient vraies. Et c’est ce que fait l’opérateur and :
(2+2 == 4) and (2+2 == 5)
Enfin, il y a l’opérateur not, qui est simple mais délicat à décrire en français. Si je vous demande de considérer mon affirmation selon laquelle « il n’est pas vrai que 2+2 = 5 », vous diriez que mon affirmation est vraie, parce qu’en fait mon affirmation est que «2+2 = 5 est fausse ». J’ai donc raison. Pour écrire ça dans Jamovi, on utilise ça :
NOT(2+2 == 5)
En d’autres termes, puisque 2+2 == 5 est une fausse déclaration, il doit être vrai que NOT(2+2 == 5) est vrai. Pour l’essentiel, ce que nous avons vraiment fait, c’est prétendre que « non faux » est la même chose que « vrai ». Évidemment, ce n’est pas tout à fait juste dans la vraie vie. Mais Jamovi vit dans un monde beaucoup plus en noir ou blanc. Pour Jamovi, tout est vrai ou faux. Aucune nuance de gris n’est autorisée.
Bien sûr, dans notre exemple 2=2 = 5, nous n’avions pas vraiment besoin d’utiliser deux opérateurs séparés « non » NOT et « Egal à » == comme. Nous aurions pu simplement utiliser l’opérateur « n’est pas égal à » != comme ça :
2+2 != 5
6.2.3 Application d’une opération logique au texte
Je tiens également à souligner brièvement que vous pouvez appliquer ces opérateurs logiques aussi bien au texte qu’aux données logiques. Nous devons simplement être un peu plus prudents pour comprendre comment Jamovi interprète les différentes opérations. Dans cette section, je vais parler de la façon dont l’opérateur « égal à » == s’applique au texte, puisque c’est le plus important. Évidemment, puisque l’opérateur « pas égal à » != donne les réponses exactement opposées à ==, alors je parle implicitement de lui aussi, mais je ne donnerai pas d’instructions spécifiques montrant l’utilisation de !=.
Bien, voyons comment ça marche. Dans un sens, c’est très simple. Par exemple, je peux demander à Jamovi si le mot « chat » est le même que le mot « chien », comme ceci :
« chat » == « chien »
C’est assez évident, et c’est bon de savoir que même Jamovi peut le découvrir. De même, Jamovi reconnaît qu’un « chat » est un « chat » :
« chat » == « chat »
Encore une fois, c’est exactement ce à quoi nous nous attendions. Cependant, ce que vous devez garder à l’esprit est que Jamovi n’est pas du tout tolérant quand il s’agit de grammaire et d’espacement. Si deux chaines diffèrent de quelque façon que ce soit, Jamovi dira qu’elles ne sont pas égales l’une à l’autre, comme dans les cas suivants :
« chat» ==« chat »
« chat » ==« CHAT »
« chat » == « c h a t »
Vous pouvez également utiliser d’autres opérateurs logiques. Par exemple, Jamovi vous permet également d’utiliser les opérateurs < et > pour déterminer laquelle des deux « chaînes » de texte vient en premier, alphabétiquement parlant. En fait, c’est un peu plus compliqué que ça, mais commençons par un exemple simple :
« chat » <« chien »
Dans Jamovi, cet exemple est considéré comme VRAI. C’est parce que « chat » vient avant « chien » dans l’ordre alphabétique que Jamovi juge que la déclaration est vraie. Cependant, si nous demandons à Jamovi de nous dire si « chat » vient avant « fourmilier » alors il évaluera l’expression comme fausse. Pour l’instant, tout va bien. Mais les données textuelles sont un peu plus compliquées que ne le suggère le dictionnaire. Qu’en est-il du « CHAT » et du « chat » ? Lequel d’entre eux vient en premier ? Essayez-le et vous le saurez :
« CAT » < « cat »
Ceci est en fait évalué comme vrai. En d’autres termes, Jamovi suppose que les lettres majuscules passent avant les minuscules. D’accord, c’est exact. Personne n’en sera surpris. Ce qui peut vous surprendre, c’est que Jamovi suppose que toutes les lettres majuscules passent avant toutes les minuscules. C’est-à-dire que si « fourmilier » < « zèbre » est une affirmation vraie, et l’équivalent en majuscules « FOURMILIER » < « ZEBRE » est également vrai, il n’est pas vrai de dire que « fourmilier » < « ZEBRE », comme l’extrait suivant l’illustre. Essayez ceci :
« fourmilier » < « ZEBRE »
Cette proposition est considérée comme « fausse », ce qui peut sembler un peu contre-intuitif. En gardant cela à l’esprit, il peut être utile de jeter un coup d’œil rapide au Tableau 6‑3 qui énumère divers caractères de texte dans l’ordre dans lequel Jamovi les traite.
Tableau 6‑3 : L’ordre des différents caractères de texte utilisés par les opérateurs < et >. Le caractère « espace », qui vient en premier sur la liste, n’est pas affiché.<a name="t63>
! « # $ % & ’ ( ) * + , - . / 0 1 2 3 4 5 6 7 8 9 : ; < = > ? @
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z [ \ ] ^ _ ’
a b c d e f g h i j k l m n o p q r s t u v w x y z } | {
6.3 Transformer et recoder une variable
Il n’est pas rare dans l’analyse des données du monde réel de constater que l’une de vos variables n’est pas tout à fait équivalente à la variable que vous voulez vraiment. Par exemple, il est souvent pratique de prendre une variable à valeur continue (p. ex. l’âge) et de la diviser en un petit nombre de catégories (p. ex. jeune, adulte, plus âgé). À d’autres moments, vous devrez peut-être convertir une variable numérique en une variable numérique différente (p. ex. vous voudrez peut-être analyser à la valeur absolue de la variable originale). Dans cette section, je décrirai quelques principales façons de faire ces choses avec Jamovi.
6.3.1 Créer une variable transformée
Le premier truc à discuter est l’idée de transformer une variable. Prise littéralement, tout ce que vous faites à une variable est une transformation, mais en pratique, cela signifie habituellement que vous appliquez une fonction mathématique relativement simple à la variable originale afin de créer une nouvelle variable qui (a) fournit une meilleure façon de décrire ce qui vous intéresse réellement, ou (b) est plus en accord avec les hypothèses des tests statistiques que vous voulez faire. Comme, à ce stade, je n’ai pas parlé des tests statistiques ou de leurs hypothèses, je vais vous montrer un exemple basé sur le premier cas.
Supposons que j’ai fait une courte étude dans laquelle je pose une seule question à 10 personnes :
Sur une échelle de 1 (fortement en désaccord) à 7 (fortement d’accord), dans quelle mesure êtes-vous d’accord avec la proposition selon laquelle « les dinosaures sont impressionnants » ?
Maintenant, chargeons et regardons les données. Le fichier de données likert.omv contient une variable unique qui contient les réponses brutes à l’échelle de Likert pour ces 10 personnes. Cependant, si vous y réfléchissez bien, ce n’est pas la meilleure façon de représenter ces réponses. En raison de la façon assez symétrique dont nous avons établi l’échelle de réponse, il y a un sens dans lequel le point médian de l’échelle aurait dû être codé 0 (sans opinion), et les deux paramètres devraient être +3 (fortement d’accord) et -3 (fortement en désaccord). En recodant les données de cette façon, on reflète un peu mieux la façon dont nous pensons vraiment aux réponses. Le recodage ici est assez simple, il suffit de soustraire 4 des scores bruts. Dans Jamovi vous pouvez le faire en calculant une nouvelle variable : cliquez sur le bouton « Data » - « Compute » et vous verrez qu’une nouvelle variable a été ajoutée à la feuille de calcul. Appelons cette nouvelle variable likert.centred (saisissez son nom) et ajoutons ce qui suit dans la boîte de formule, comme dans la Figure 6‑5: « likert.raw – 4 ».
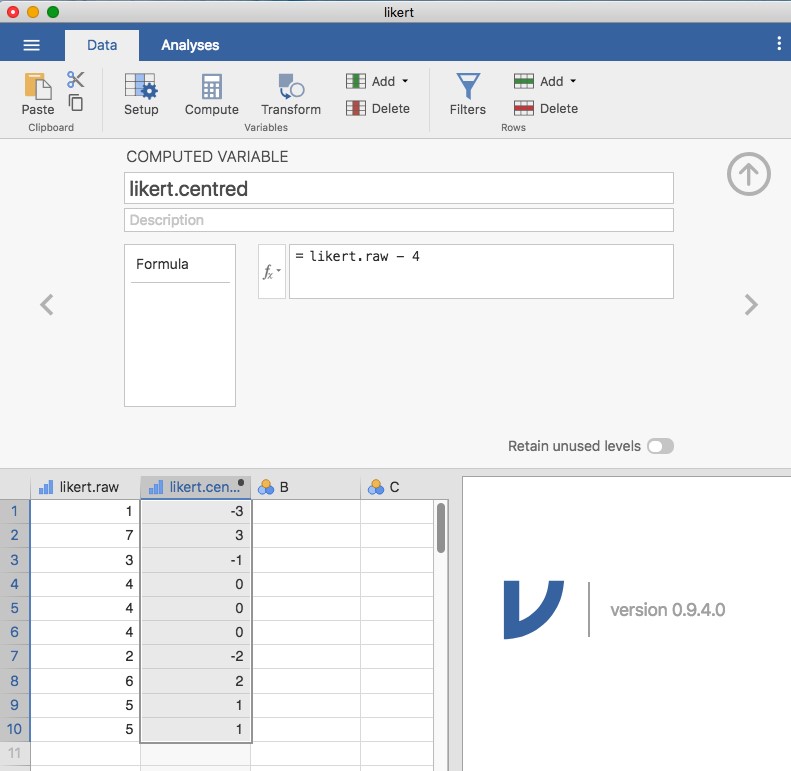
Figure 6‑5 : Créer une nouvelle variable calculée dans Jamovi
L’une des raisons pour lesquelles il pourrait être utile d’avoir les données dans ce format est qu’il existe de nombreuses situations où vous pourriez préférer analyser la force de l’opinion séparément de la direction de l’opinion. Nous pouvons faire deux transformations différentes sur cette variable likert.centred afin de distinguer ces deux concepts différents. Tout d’abord, pour calculer une variable opinion.strength, nous voulons prendre la valeur absolue des données centrées (en utilisant la fonction « ABS »).36 Dans Jamovi, créez une autre variable en utilisant le bouton « Compute ». Nommez la variable opinion.strength et cette fois, cliquez sur le bouton « fx » à côté de la case « Formula ». Ceci montre les différentes « Fonctions » et « Variables » que vous pouvez ajouter à la boîte « Formula », double-cliquez donc sur « ABS » puis double-cliquez sur likert.centred et vous verrez que la boîte « Formula » se remplit avec ABS(likert.centred) et qu’une nouvelle variable a été créée dans la feuille de calcul, comme dans Figure 6‑6:
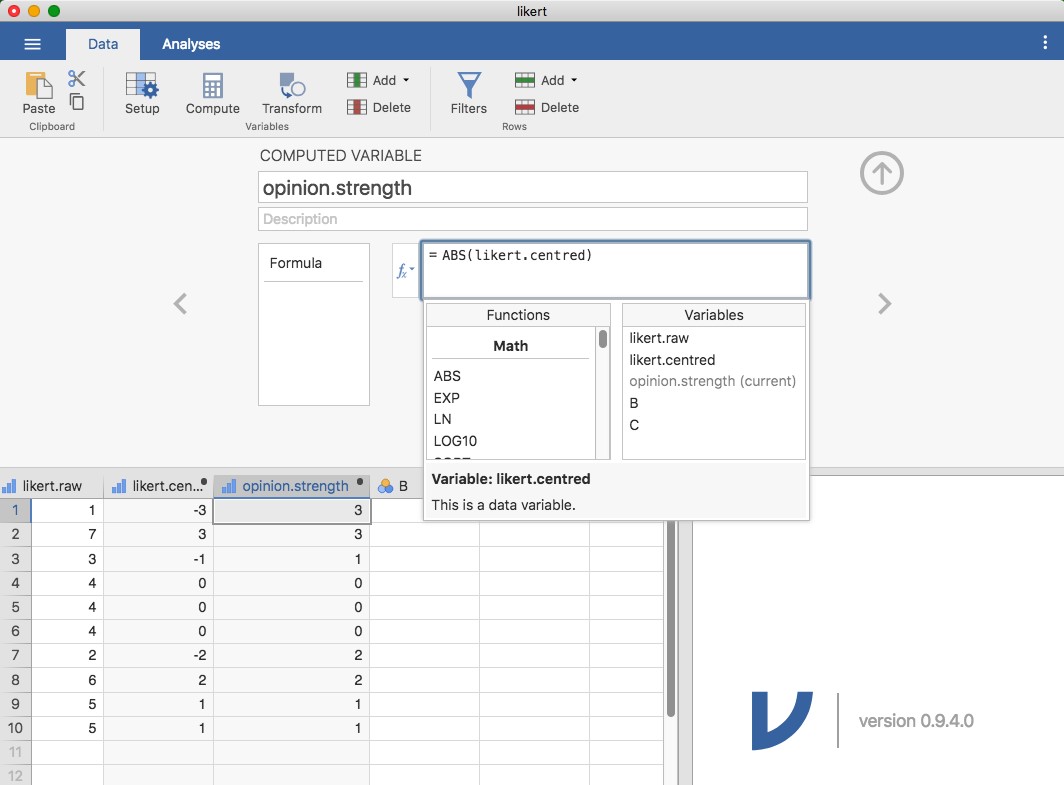
Figure 6‑6 : Sélection de fonctions et de variables à l’aide du bouton fx
Deuxièmement, pour calculer une variable qui ne contient que la direction de l’opinion et ignore la force, nous voulons calculer le « signe » de la variable. Dans Jamovi nous pouvons utiliser la fonction IF pour cela. Créez une autre variable à l’aide du bouton « Compute », nommez-la en opinion.sign, puis tapez ce qui suit dans la boîte de fonction :
IF(likert.centred == 0, 0, likert.centred / opinion.strength)
Une fois fait, vous verrez que tous les nombres négatifs de la variable likert.centered sont convertis en -1, tous les nombres positifs sont convertis en 1 et zéro reste à 0, comme ici :
-1 1 -1 0 0 0 -1 1 1 1
Décomposons ce que fait cette commande « IF ». Dans Jamovi il y a trois parties à une déclaration « IF », écrite ainsi « IF(expression, value, else) ». La première partie, « expression », peut être un énoncé logique ou mathématique. Dans notre exemple, nous avons spécifié « likert.centred == 0 », ce qui est VRAI pour les valeurs où likert.centered est zéro. La partie suivante, « value », est la nouvelle valeur à retourner lorsque l’expression dans la première partie est VRAIE. Dans notre exemple, nous avons dit que pour toutes les valeurs où likert.centred est zéro, les gardez à zéro. Dans la partie suivante, « else », nous pouvons entrer une autre instruction logique ou mathématique à utiliser si la première partie a pour résultat FAUX, c’est-à-dire les cas où likert.centred n’est pas nul. Dans notre exemple, nous avons divisé likert.centred par opinion.strength pour obtenir « -1 » ou « +1 » selon le signe de la valeur originale dans likert.centred.37
Et c’est fini. Nous avons maintenant trois nouvelles variables géniales, qui sont toutes des transformations utiles des données originales de likert.raw.
6.3.2 Réduire une variable en un plus petit nombre de niveaux ou en catégories discrètes
Une tâche pratique qui revient assez souvent est le problème du regroupement d’une variable en un plus petit nombre de niveaux ou de catégories distincts. Par exemple, supposons que je m’intéresse à la répartition par âge des participants à une réunion sociale :
60, 58, 24, 26, 34, 42, 31, 30, 33, 2, 9
Dans certaines situations, il peut être très utile de les regrouper en un petit nombre de catégories. Par exemple, nous pourrions regrouper les données en trois grandes catégories : jeunes (0-20 ans), adultes (21-40 ans) et plus âgés (41-60 ans). Il s’agit d’une classification assez grossière, et les étiquettes que j’ai jointes n’ont de sens que dans le contexte de cet ensemble de données (p. ex. en général, une personne de 42 ans ne se considérerait pas comme étant « plus âgés »). Nous pouvons découper cette variable en tranches assez facilement en utilisant la fonction Jamovi « IF » que nous avons déjà utilisée. Cette fois, nous devons spécifier des instructions « IF » imbriquées, ce qui signifie simplement que SI la première expression logique est VRAIE, insérer une première valeur, mais SI une deuxième expression logique est VRAIE, insérer une deuxième valeur, mais SI une troisième expression logique est VRAIE, insérer ensuite une troisième valeur. Cela peut s’écrire comme suit :
IF(Age >= 0 et Age <= 20, 1, IF(Age >= 21 ans et Age <= 40 ans, 2, IF(Age >= 41 ans et Age <= 60 ans, 3))))
Notez qu’il y a trois parenthèses gauches utilisées dans l’imbrication, donc l’instruction entière doit se terminer par trois parenthèses droites sinon vous aurez un message d’erreur. La capture d’écran Jamovi de cette manipulation de données, ainsi qu’un tableau de fréquences l’accompagnant, est présentée à la Figure 6‑7.
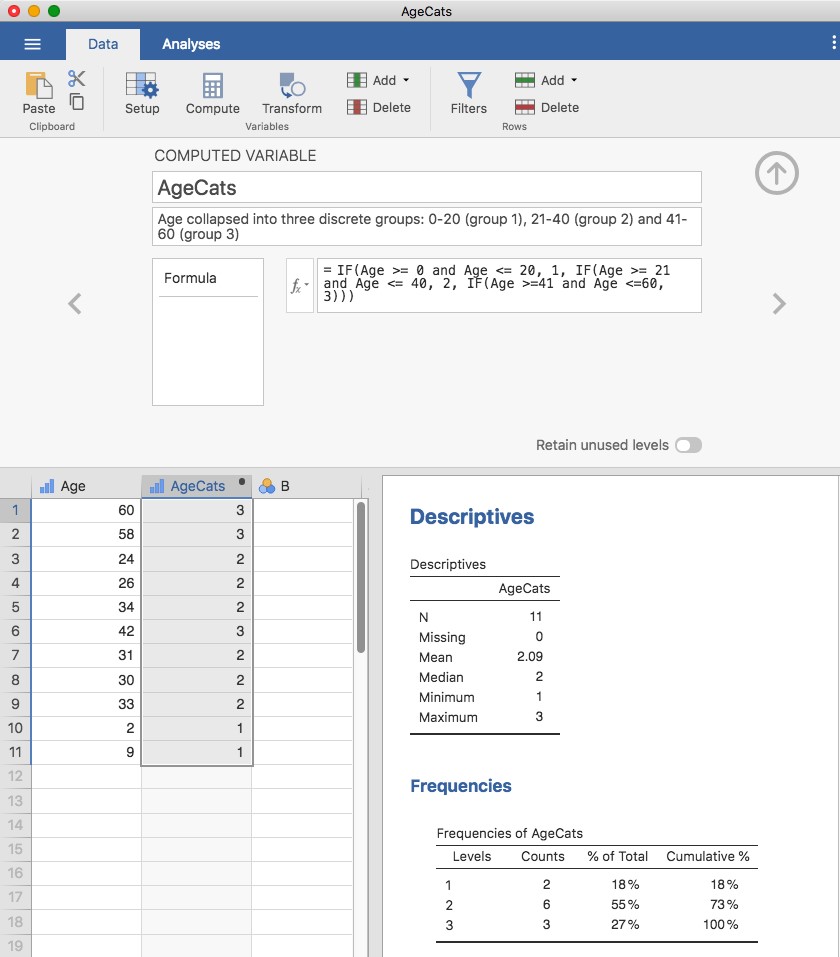
Figure 6‑7 : Réduire une variable en un plus petit nombre de niveaux discrets à l’aide de la fonction « IF » de Jamovi
Il est important de prendre le temps de déterminer si les catégories qui en résultent ont un sens pour votre projet de recherche. Si elles n’ont aucun sens pour vous en tant que catégories, alors toute analyse de données qui utilise ces catégories est susceptible d’être tout aussi dénuée de sens. Plus généralement, dans la pratique, j’ai remarqué que les gens ont un désir très fort de découper leurs données (continues et désordonnées) en quelques catégories (discrètes et simples), puis d’effectuer des analyses en utilisant les données catégorisées plutôt que les données originales.38 Je n’irais pas jusqu’à dire qu’il s’agit d’une mauvaise idée en soi, mais elle comporte parfois des inconvénients assez graves, je vous conseille donc de faire preuve de prudence si vous envisagez de le faire.
6.3.3 Créer une transformation qui peut être appliquée à plusieurs variables
Parfois, vous voulez appliquer la même transformation à plus d’une variable, par exemple lorsque vous avez plusieurs items de questionnaire qui doivent tous être recalculés ou recodés de la même manière. L’une des caractéristiques intéressantes de Jamovi est que vous pouvez créer une transformation, en utilisant le bouton « Data » - « Transform », qui peut ensuite être enregistrée et appliquée à plusieurs variables. Revenons au premier exemple ci-dessus, en utilisant le fichier de données likert.omv qui contient une seule variable avec des réponses brutes à l’échelle de Likert pour 10 personnes. Pour créer une transformation que vous pouvez enregistrer puis appliquer à plusieurs variables (en supposant que vous ayez plus de variables de ce type dans votre fichier de données), sélectionnez d’abord dans l’éditeur de feuille de calcul (c’est-à-dire cliquez sur) la variable que vous voulez utiliser pour créer initialement la transformation. Dans notre exemple, il s’agit de likert.raw. Cliquez ensuite sur le bouton « Transform » dans le ruban Jamovi « Data », et vous devriez avoir quelque chose comme sur la Figure 6‑8.
Donnez un nom à votre nouvelle variable, appelons-la opinion.strength, puis cliquez sur la case de sélection « Using transform » et sélectionnez « Create New Transform… ». C’est ici que vous allez créer, et nommer, la transformation qui peut être réappliquée à autant de variables que vous le souhaitez. La transformation est automatiquement nommée pour nous comme « Transform 1 » (Bien pensé, non ? Vous pouvez changer ceci si vous voulez). Tapez ensuite l’expression « ABS($source - 4) » dans la zone de texte de la fonction, comme dans la Figure 6‑9, appuyez sur Entrée ou Retour sur votre clavier et, rapidement, vous avez créé une nouvelle transformation et l’avez appliquée à la variable likert.raw ! Bien ! Notez qu’au lieu d’utiliser l’étiquette de la variable dans l’expression, nous avons plutôt utilisé « $source ». C’est pour que nous puissions ensuite utiliser la même transformation avec autant de variables différentes que nous le souhaitons - Jamovi vous demande d’utiliser « $source » pour faire référence à la variable source que vous transformez. Votre transformation a également été sauvegardée et peut être réutilisée à tout moment (à condition que vous sauvegardiez l’ensemble de données dans un fichier « .omv », sinon vous la perdrez !
Vous pouvez également créer une transformation à l’aide du deuxième exemple que nous avons examiné, la répartition par âge des participants à une réunion sociale. Essayez si vous en avez envie ! N’oubliez pas que nous avons regroupé cette variable en trois groupes : les jeunes, les adultes et les plus âgés. Cette fois-ci, nous allons faire la même chose, mais en utilisant le bouton « Transform » - « Add condition » de Jamovi. Avec cet ensemble de données (y retourner ou le créer à nouveau si vous ne l’avez pas sauvegardé), configurez une nouvelle transformation de variable. Appelez la variable transformée AgeCats et la transformation que vous allez créer Agegroupings. Cliquez ensuite sur le grand signe « + » à côté de la case de fonction. C’est le bouton « Add condition » et j’ai collé une grosse flèche rouge sur la Figure 6‑10 pour que vous puissiez voir exactement où cela se trouve. Recréez la transformation illustrée à la Figure 6‑10 et lorsque vous aurez terminé, vous verrez apparaître les nouvelles valeurs dans la fenêtre du tableur.
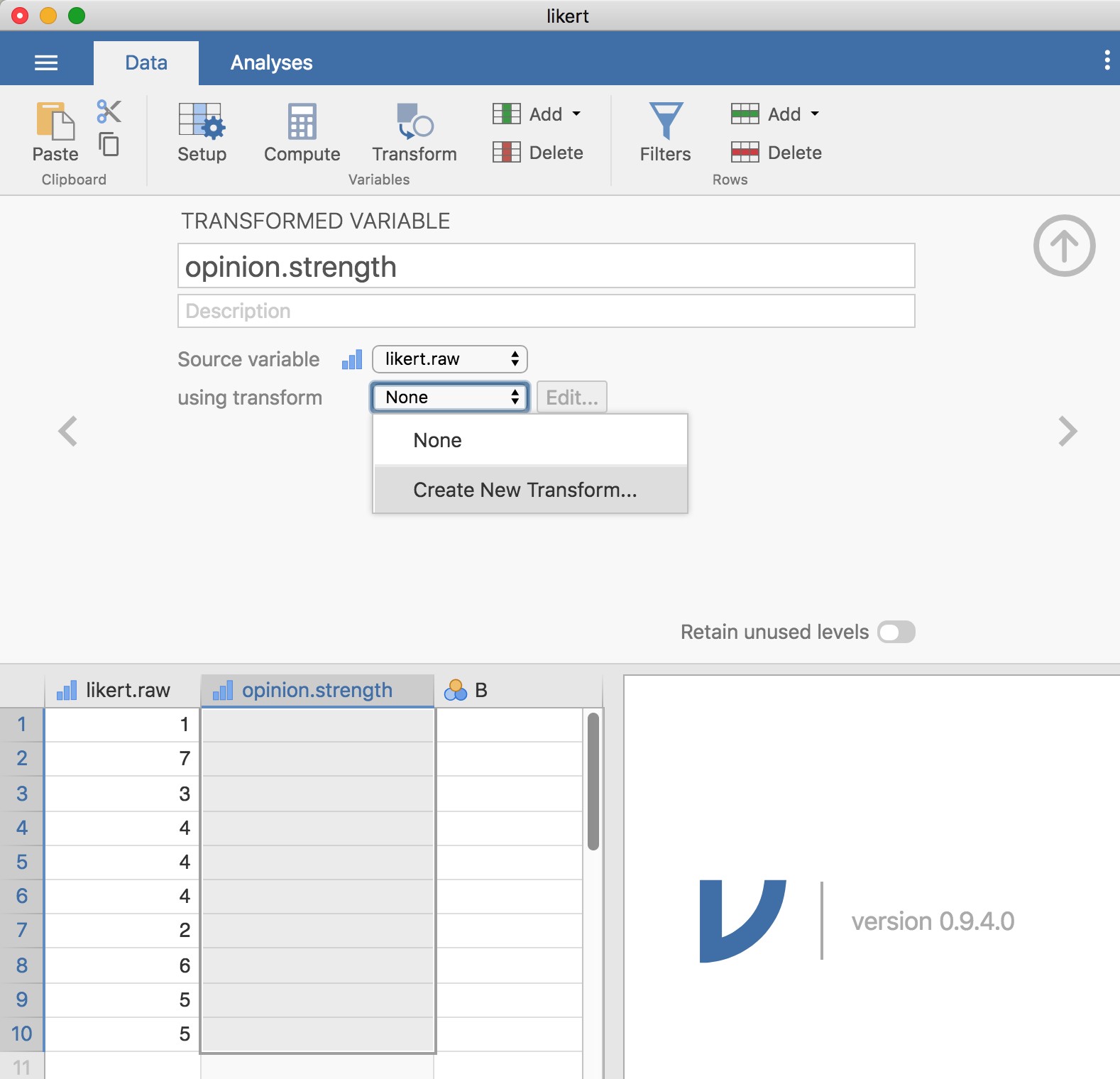
Figure 6‑8 : Création d’une nouvelle transformation de variable à l’aide de la commande Jamovi « Transform ».
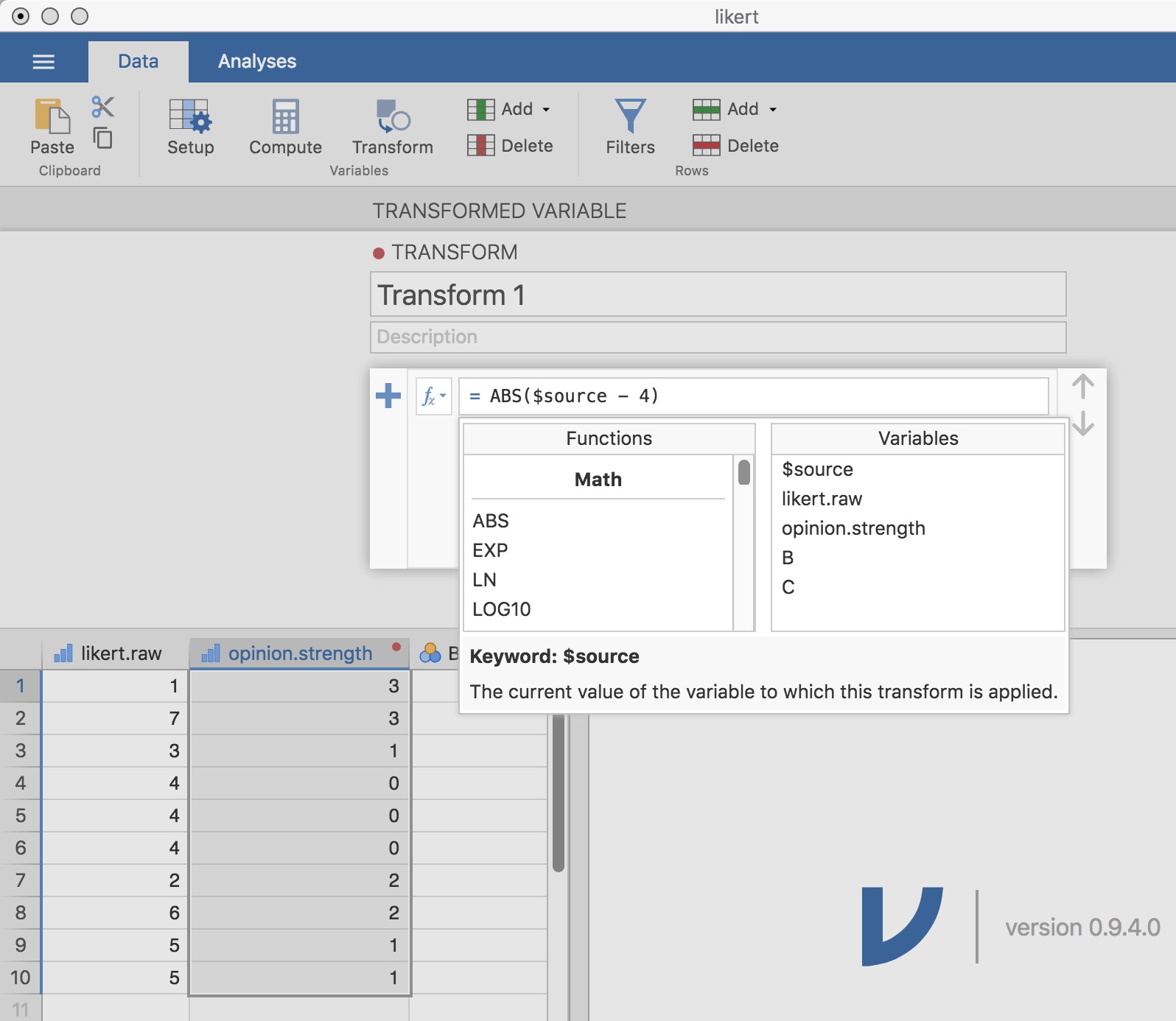
Figure 6‑9 : Spécification d’une transformation dans Jamovi, à sauvegarder sous le nom imaginaire « Transform 1 ».
De plus, la transformation des groupes d’âge a été sauvegardée et peut être réappliquée à tout moment. Entendu, je sais qu’il est peu probable que vous ayez plus d’une variable « Age », mais vous savez maintenant comment configurer les transformations dans Jamovi, donc vous pouvez suivre cet exemple avec d’autres types de variables. Un scénario typique est celui où vous avez un questionnaire avec des échelles, disons, 20 items (variables) et chaque item a été initialement noté de 1 à 6 mais, pour une raison ou une autre, vous décidez de recoder tous les items de 1 à 3. Vous pouvez facilement le faire avec Jamovi en créant puis en appliquant de nouveau votre transformation pour chaque variable que vous voulez recoder.
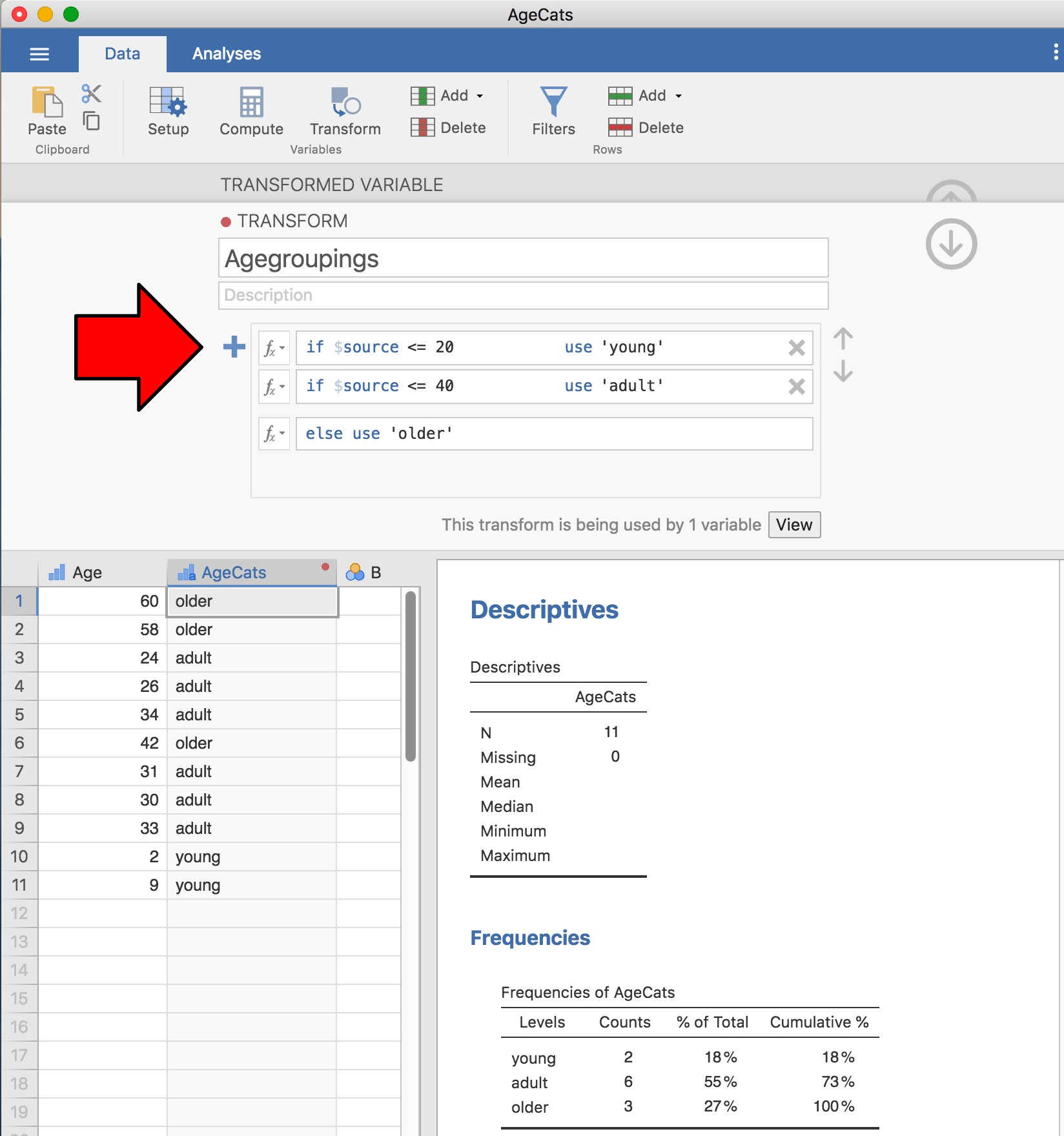
Figure 6‑10 : Transformation de Jamovi en trois catégories d’âge, à l’aide du bouton ‘Ajouter condition’.
Tableau 6‑4 : Certaines des fonctions mathématiques disponibles dans Jamovi
| fonction | exemple d’entrée | (réponse) | |
| racine carrée | SQRT(x) | SQRT(25) | 5 |
| valeur absolue | ABS(x) | ABS(-23) | 23 |
| logarithme (base 10) | LOG10(x) | LOG10(1000) | 3 |
| logarithme (base e) | LN(x) | LN(1000) | 6.908 |
| exponentiation | EXP(x) | EXP(6.908) | 1000.245 |
| box-cox | BOXCOX(x, lamda) | BOXCOX(6.908, 3) | 109.551 |
6.4 Quelques fonctions et opérations mathématiques supplémentaires
Dans la section 6.3, j’ai discuté des idées qui sous-tendent les transformations des variables et j’ai montré qu’un grand nombre des transformations que vous pourriez vouloir appliquer à vos données sont basées sur des fonctions et opérations mathématiques assez simples. Dans cette section, je veux revenir sur cette discussion et mentionner plusieurs autres fonctions mathématiques et opérations arithmétiques qui sont en fait très utiles pour beaucoup d’analyses de données réelles. Le Tableau 6‑4 donne un bref aperçu des diverses fonctions mathématiques dont je veux parler ici ou plus loin.39 Évidemment, cela ne constituent pas un catalogue complet des possibilités disponibles, mais cela couvre un éventail de fonctions qui sont utilisées régulièrement dans l’analyse des données et qui sont disponibles dans Jamovi.
6.4.1 Logarithmes et exponentielles
Comme je l’ai mentionné plus tôt, Jamovi possède une gamme pratique de fonctions mathématiques intégrées et il ne serait pas vraiment utile d’essayer de les décrire ou même de les énumérer toutes. Pour l’essentiel, je me suis concentré uniquement sur les fonctions qui sont strictement nécessaires pour ce livre. Cependant, je veux faire une exception pour les logarithmes et les exponentielles. Bien qu’ils ne soient nécessaires nulle part ailleurs dans ce livre, ils sont partout dans les statistiques. En plus, il y a beaucoup de situations dans lesquelles il est pratique d’analyser le logarithme d’une variable (c’est-à-dire de prendre une « log-transformation » de la variable). Je soupçonne que beaucoup (peut-être la plupart) des lecteurs de ce livre ont déjà rencontré des logarithmes et des exponentielles auparavant, mais d’après mon expérience passée, je sais qu’il y a une proportion importante d’étudiants qui suivent un cours de statistiques en sciences sociales et qui n’ont pas touché aux logarithmes depuis le secondaire, et j’aimerais faire un petit rappel.
Pour comprendre les logarithmes et les exponentielles, le plus simple est de les calculer et de voir comment ils se rapportent à d’autres calculs simples. Il y a trois fonctions Jamovi en particulier dont je veux parler, à savoir LN(), LOG10() et EXP(). Pour commencer, considérons LOG10(), qui est connu sous le nom de « logarithme en base 10 ». L’astuce pour comprendre un logarithme est de comprendre qu’il s’agit essentiellement du « contraire » l’élévation à la puissance. Plus précisément, le logarithme en base 10 est étroitement lié aux puissances de 10. Commençons donc par noter que 10 au cube, c’est 1000. Mathématiquement, on écrirait ceci :
\[ 10^{3} = 1000 \]
L’astuce pour comprendre un logarithme est de reconnaître que l’affirmation que « 10 à la puissance de 3 est égale à 1000 » est équivalente à l’affirmation que « le logarithme (en base 10) de 1000 est égal à 3 ». Mathématiquement, nous écrivons ceci comme suit,
\[ \operatorname{}{\left( 1000 \right) - 3} \]
Bien, puisque la fonction LOG10() est liée aux puissances de 10, vous pouvez vous attendre à ce qu’il y ait d’autres logarithmes (dans des bases autres que 10) qui sont également liés aux autres puissances. Et bien sûr, c’est vrai : il n’y a rien de mathématiquement spécial dans le chiffre 10. Il se trouve que vous et moi le trouvons utile parce que les nombres décimaux sont construits autour du chiffre 10, mais le terrible monde des mathématiques se moque de nos nombres décimaux. Malheureusement, l’univers ne se soucie pas vraiment de la façon dont nous écrivons les chiffres. Quoi qu’il en soit, la conséquence de cette indifférence cosmique est qu’il n’y a rien de particulier à calculer les logarithmes en base 10. Vous pourriez, par exemple, calculer vos logarithmes en base 2. Alternativement, un troisième type de logarithme, et on en voit beaucoup plus dans les statistiques que la base 10 ou la base 2, s’appelle le logarithme naturel, et correspond au logarithme de la base e. Comme vous pourriez un jour le rencontrer, je ferais mieux de vous expliquer ce qu’est e. Le nombre e, connu sous le nom de nombre d’Euler, est l’un de ces nombres « irrationnels » ennuyeux dont l’expansion décimale est infiniment longue, et est considéré comme l’un des nombres les plus importants en mathématiques. Les premiers chiffres de e sont :
e = 2,718282
Il y a pas mal de situation dans les statistiques qui nous obligent à calculer les puissances de e, bien qu’aucun d’entre eux n’apparaissent dans ce livre. Elever e à la puissance x s’appelle l’exponentielle de x, et il est donc très commun de voir ex écrit comme exp(x). Il n’est donc pas surprenant que Jamovi ait une fonction qui calcule les exponentielles, appelée EXP(). Étant donné que le nombre e apparaît si souvent dans les statistiques, le logarithme naturel (c.-à-d. le logarithme en base e) a aussi tendance à apparaître. Les mathématiciens l’écrivent souvent comme loge(x) ou ln(x). En fait, Jamovi fonctionne de la même manière : la fonction LN() correspond au logarithme naturel.
Et avec ça, je pense que nous avons eu assez d’exponentielles et de logarithmes pour ce livre !
6.5 Extraction d’un sous-ensemble de données
Un type très important de traitement des données est la possibilité d’extraire un sous-ensemble particulier de données. Par exemple, vous pourriez n’être intéressé que par l’analyse des données d’une condition expérimentale, ou vous pourriez vouloir examiner de près les données de personnes âgées de plus de 50 ans. Pour ce faire, la première étape consiste à faire filtrer avec Jamovi le sous-ensemble des données correspondant aux observations qui vous intéressent.
Cette section revient sur l’ensemble de données nightgarden.csv. Si vous lisez tout ce chapitre en une seule fois, alors vous devriez déjà avoir cet ensemble de données chargé dans une fenêtre Jamovi. Pour cette section, concentrons-nous sur les deux variables speaker et Utterance (voir Section 6.1 si vous avez oublié à quoi ressemblent ces variables). Supposons que ce que je veuille faire, c’est retirer seulement les énoncés qui ont été faits par Makka-Pakka. Pour cela, nous devons spécifier un filtre dans Jamovi. Ouvrez d’abord une fenêtre de filtre en cliquant sur « Filters » dans la barre d’outils principale Jamovi « Data ». Puis, dans la zone de texte « Filter 1 », à côté du signe « = », tapez ce qui suit :
speaker ==‘makka-pakka’.
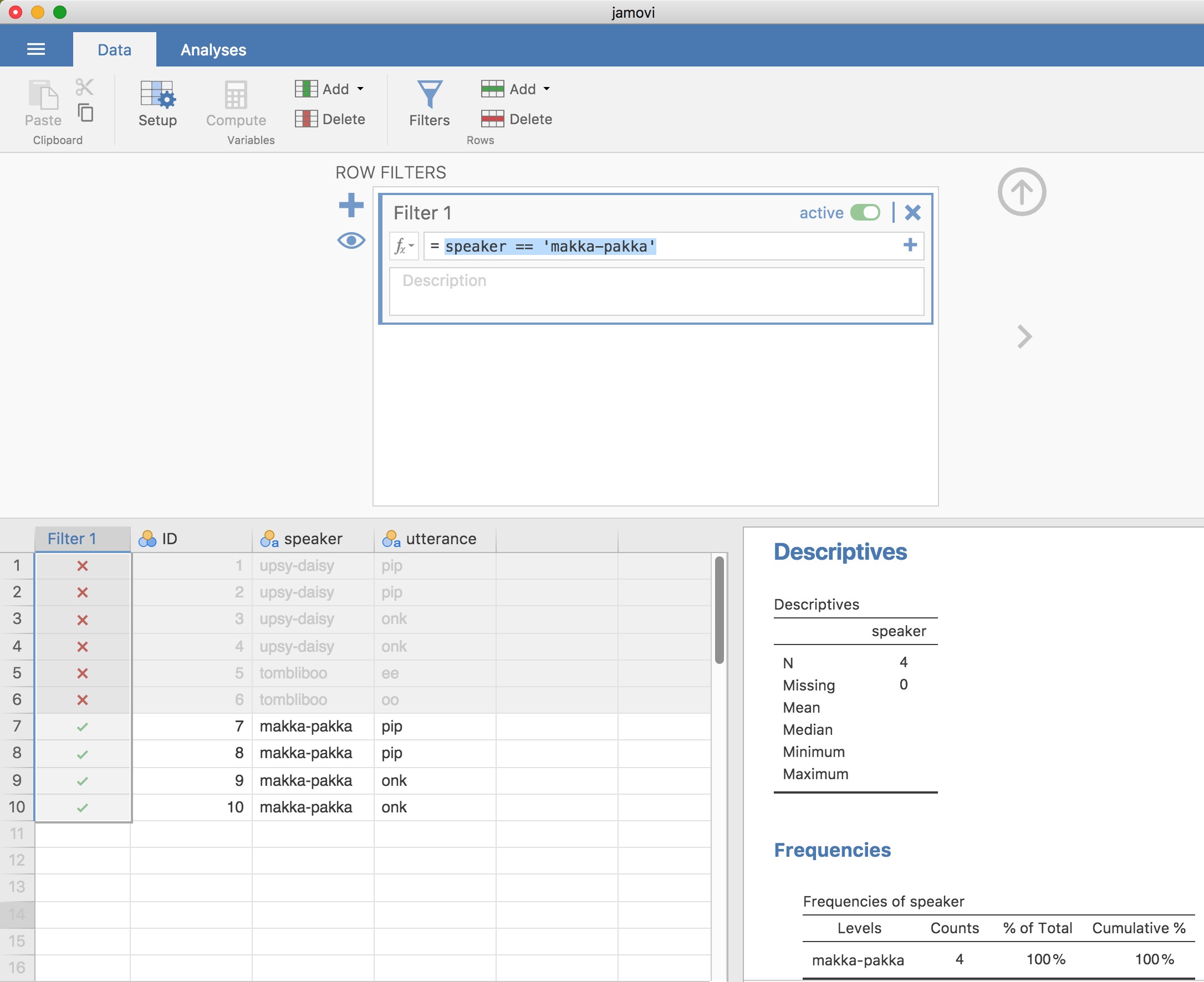
Figure 6‑11 : Création d’un sous-ensemble de données de jardin de nuit à l’aide de l’option Jamovi ‘Filters’.
Une fois cette opération terminée, vous verrez qu’une nouvelle colonne a été ajoutée à la fenêtre du tableur (voir Figure 6‑11), intitulée « Filter 1 », avec les cas où le speaker n’est pas « makka-pakka « grisée (c’est-à-dire filtrée) et, inversement, où le speaker est « makka-pakka «, avec une coche verte indiquant que le filtre est activé. Vous pouvez tester ceci en exécutant « Exploration’’Descriptifs » - « Tableaux de fréquences » pour la variable speaker et voir ce que cela indique. Allez-y, essayez-le !
En suivant cet exemple simple, vous pouvez aussi construire des filtres plus complexes en utilisant des expressions logiques de Jamovi. Par exemple, supposons que je veuille garder seulement les cas où l’énoncé est « pip » ou « oo ». Dans ce cas, dans la zone de texte « Filter 1 », à côté du signe « = », vous devez taper ce qui suit :
prononciation ==‘pip’ ou prononciation ==‘oo’.
6.6 Résumé
Il est évident que ce chapitre n’a pas vraiment de cohérence. C’est juste un ensemble de sujets et d’astuces qu’il peut être utile de connaître, alors le meilleur résumé que je puisse donner ici est de répéter cette liste :
- Section 6.1. Mise en tableau des données.
- Section 6.2. Utiliser des expressions logiques.
- Section 6.3. Transformer ou recoder une variable.
- Section 6.4. Quelques fonctions mathématiques utiles.
- Section 6.5. Extraction d’un sous-ensemble d’un ensemble de données.
La citation provient de Home is the Hangman, publié en 1975.↩︎
J’offre mes tentatives d’adolescence d’être « cool » comme preuve que certaines choses ne peuvent tout simplement pas être faites.↩︎
Vous pouvez le faire dans l’écran Calculer nouvelle variable, bien que calculer 2 + 2 pour chaque cellule d’une nouvelle variable ne soit pas très utile !↩︎
Voilà une bizarrerie de Jamovi. Lorsque vous avez des expressions logiques simples comme celles que nous avons déjà rencontrées, par exemple 2 + 2 == 5, Jamovi indique clairement « FAUX » (ou « VRAI ») dans la colonne correspondante de la feuille de calcul. Lorsque nous avons des expressions logiques plus complexes, telles que (2+2 == 4) ou (2+2 == 5), Jamovi affiche simplement 0 ou 1, selon que l’expression logique est évaluée comme fausse, ou vraie.↩︎
La valeur absolue d’un nombre est sa distance à zéro, alors que son signe est négatif ou positif.↩︎
La raison pour laquelle nous devons utiliser la commande’IF’ et garder zéro comme zéro est que vous ne pouvez pas simplement utiliser likert.centred / opinion.strength pour calculer le signe de likert.centrred, car la division mathématique de zéro par zéro ne fonctionne pas. Essayez-le et vous verrez↩︎
Si vous avez lu plus loin dans le livre, et que vous relisez cette section, alors un bon exemple de cela serait que quelqu’un choisisse de faire une analyse de variance en utilisant AgeCats comme variable de regroupement, au lieu de faire une régression en utilisant Age comme prédicteur. Il y a parfois de bonnes raisons de le faire. Par exemple, si la relation entre l’âge et votre variable de résultat est très non linéaire et que vous n’êtes pas à l’aise d’essayer de faire une régression non linéaire ! Cependant, à moins que vous n’ayez vraiment une bonne raison de le faire, il vaut mieux ne pas le faire. Elle tend à introduire toutes sortes d’autres problèmes (par exemple, les données violeront probablement l’hypothèse de normalité) et vous pouvez perdre beaucoup de puissance statistique.↩︎
Nous laisserons la fonction box-cox à plus tard, voir section 12.10.4.↩︎