Chapitre 10 Analyse des données catégoriques

Maintenant que nous avons couvert la théorie de base qui sous-tend les tests d’hypothèse, il est temps de commencer à examiner des tests spécifiques qui sont couramment utilisés en psychologie. Par où devrions-nous commencer ? Tous les manuels ne s’entendent pas sur les points de départ, mais je vais commencer par « les test de \(\chi^{2}\) » (ce chapitre, prononcé « chi-carré »⁶⁶) et « les tests de t » (chapitre 11. Ces deux outils sont très fréquemment utilisés dans la pratique scientifique, et bien qu’ils ne soient pas aussi puissants que la « régression » (chapitre 12) et « l’analyse de variance » (chapitre 13), ils sont beaucoup plus faciles à comprendre.

Le terme « données catégorielles » n’est qu’un autre nom pour « données d’échelle nominale ». Ce n’est rien dont nous n’avons pas déjà discuté, c’est juste que dans le contexte de l’analyse des données, les gens ont tendance à utiliser le terme « données catégorielles » plutôt que « données à échelle nominale ». Je ne sais pas pourquoi. Dans tous les cas, l’analyse catégorielle des données fait référence à un ensemble d’outils que vous pouvez utiliser lorsque vos données sont sur une échelle nominale. Cependant, il existe de nombreux outils différents qui peuvent être utilisés pour l’analyse des données catégorielles, et ce chapitre ne couvre que quelques-uns des plus courants.

10.1 Le test d’adéquation \(\chi^{2}\) (chi carré)

Le test d’adéquation \(\chi^{2}\) est l’un des plus anciens tests d’hypothèse. Il a été inventé par Karl Pearson au tournant du siècle (Pearson 1900), avec quelques corrections apportées plus tard par Sir Ronald Fisher (Fisher 1922). Il vérifie si une distribution de fréquence observée d’une variable nominale correspond à une distribution de fréquence attendue. Par exemple, supposons qu’un groupe de patients a subi un traitement expérimental et que leur état de santé a été évalué pour voir si leur état s’est amélioré, s’il est demeuré le même ou s’il s’est aggravé. Un test d’adéquation pourrait être utilisé pour déterminer si les chiffres dans chaque catégorie - améliorés, sans changement, aggravés - correspondent aux chiffres auxquels on pourrait s’attendre avec l’option de traitement standard. Réfléchissons encore un peu, avec un peu de psychologie.

10.1.1 Les données des cartes

Au fil des ans, de nombreuses études ont montré que les humains ont de la difficulté à simuler le hasard. Si nous essayons « d’agir » au hasard, nous pensons en termes de modèles et de structure et donc, quand on nous demande de « faire quelque chose au hasard », ce que les gens font en réalité est tout sauf aléatoire. En conséquence, l’étude de l’aléatoire humain (ou de la non aléatoire, selon le cas) soulève beaucoup de questions psychologiques profondes sur la façon dont nous pensons le monde. En gardant cela à l’esprit, considérons une étude très simple. Supposons que je demande aux gens d’imaginer un jeu de cartes mélangé, et de choisir mentalement une carte dans ce jeu imaginaire « au hasard ». Après avoir choisi une carte, je leur demande d’en choisir une deuxième mentalement. Pour les deux choix, ce que nous allons regarder, c’est la couleur (coeur, trèfle, pique ou carreau) que les gens ont choisi. Après avoir demandé, disons, à N=200 personnes de le faire, j’aimerais regarder les données et déterminer si les cartes que les gens prétendaient choisir étaient vraiment aléatoires. Les données sont contenues dans le fichier randomness.csv dans lequel, lorsque vous l’ouvrez dans Jamovi et regardez la feuille de calcul, vous verrez trois variables. Il s’agit d’une variable id qui attribue un identifiant unique à chaque participant et des deux variables choice_1 et choice_2 qui indiquent les combinaisons de cartes choisies par les participants.

Pour l’instant, concentrons-nous sur le premier choix que les gens ont fait. Nous utiliserons l’option Tableaux de fréquence sous « Exploration » - « Descriptive » pour compter le nombre de fois où nous avons observé des gens choisir chaque combinaison. Voilà ce qu’on obtient :

Trèfle	Carreau	Coeur	Pique
35	51	64	50

Ce petit tableau de fréquence est très utile. En y regardant de plus près, il y a un indice que les sujets sont plus enclins à choisir des cœurs que des trèfles, mais ce n’est pas tout à fait évident que ce soit réellement vrai, ou si que ce soit le fruit du hasard. Nous devrons donc probablement faire une sorte d’analyse statistique pour le découvrir, ce dont je vais vous parler dans la prochaine section.

Très bien. À partir de maintenant, nous traiterons ce tableau comme les données que nous cherchons à analyser. Cependant, comme je vais devoir parler de ces données en termes mathématiques (désolé !), ce serait bien d’être clair sur la notation. En notation mathématique, on raccourcit le mot « observé » lisible par l’homme par la lettre O, et on utilise des indices pour indiquer la position de l’observation. Ainsi, la deuxième observation de notre tableau s’écrit O₂ en mathématiques. La relation entre les descriptions en langage nature et les symboles mathématiques est illustrée ci-dessous :

Intitulé	indice, i	symbole mathématique	la valeur
Trèfles	1	O1	35
Carreaux	2	O2	51
Cœurs	3	O3	64
Piques	4	O4	50

J’espère que c’est assez clair. Il est également intéressant de noter que les mathématiciens préfèrent parler de choses générales plutôt que spécifiques, de sorte que vous verrez aussi la notation O_i, qui se réfère au nombre d’observations qui entrent dans la i-ème catégorie (où i pourrait être 1, 2, 3 ou 4). Enfin, si l’on veut se référer à l’ensemble des fréquences observées, les statisticiens regroupent toutes les valeurs observées dans un vecteur⁶⁷, que je vais appeler O.

\[O=(O_{1},O_{2},O_{3},O_{4})\]

Encore une fois, Il n’y a rien de nouveau ou de particulier. C’est juste une notation. Si je dis que O=(35, 51 ,64,50) tout ce que je fais est de décrire le tableau des fréquences observées (c’est-à-dire observées), mais je m’y réfère en utilisant la notation mathématique.

10.1.2 L’hypothèse nulle et l’hypothèse alternative

Comme l’indique la dernière section, notre hypothèse de recherche est que « les gens ne choisissent pas les cartes au hasard ». Ce que nous allons maintenant vouloir faire, c’est traduire cela en hypothèses statistiques, puis construire un test statistique de ces hypothèses. Le test que je vais vous décrire est le test d’adéquation de Pearson \(\chi^{2}\) (chi carré), et comme c’est souvent le cas, nous devons commencer par construire soigneusement notre hypothèse nulle. Dans ce cas, c’est assez facile. Tout d’abord, énonçons l’hypothèse nulle avec des mots :

H₀: Les quatre couleurs sont choisies avec une probabilité égale

Maintenant, comme il s’agit de statistiques, nous devons pouvoir dire la même chose d’une manière mathématique. Pour ce faire, utilisons la notation P_J pour faire référence à la véritable probabilité que la j-ième couleur soit choisie. Si l’hypothèse nulle est vraie, alors chacune des quatre couleurs a 25% de chance d’être sélectionnée. En d’autres termes, notre hypothèse nulle prétend que P₁=.25, P₂=.25, P₃=.25 et enfin que P₄=.25. Cependant, de la même manière que nous pouvons regrouper nos fréquences observées dans un vecteur O qui résume l’ensemble des données, nous pouvons utiliser P pour nous référer aux probabilités qui correspondent à notre hypothèse nulle. Donc si je laisse le vecteur P=(P₁, P₂, P₃, P₄) se référer à l’ensemble des probabilités qui décrivent notre hypothèse nulle, alors nous avons :

\[H_{0} : P = (.25, .25, .25, .25)\] Dans ce cas particulier, notre hypothèse nulle correspond à un vecteur de probabilités P dans lequel toutes les probabilités sont égales entre elles. Mais ce n’est pas forcément le cas. Par exemple, si la tâche expérimentale consistait pour les gens à imaginer qu’ils tiraient des cartes d’un jeu qui avait deux fois plus de trèfles que toute autre couleur, alors l’hypothèse nulle correspond à quelque chose comme P= (.4, .2, .2, .2). Tant que les probabilités sont toutes des nombres positifs, et qu’elles totalisent toutes 1, alors c’est un choix parfaitement légitime pour l’hypothèse nulle. Toutefois, l’utilisation la plus courante du test de la qualité de l’ajustement consiste à vérifier une hypothèse nulle selon laquelle toutes les catégories sont également probables, et nous nous en tiendrons donc à cela pour notre exemple.

Et notre hypothèse alternative, H₁ ? Tout ce qui nous intéresse vraiment, c’est de démontrer que les probabilités en jeu ne sont pas toutes identiques (c’est-à-dire que les choix des gens n’étaient pas complètement aléatoires). En conséquence, les versions « humaine » de nos hypothèses ressemblent à ceci :

• H₀ : Les quatre couleurs sont choisies avec une probabilité égale
• H₁ : Au moins un des choix de la combinaison n’a pas une probabilité de 0,25

et la version « mathématique » est :

\[\begin{aligned} H_{0} : P = (.25, .25, .25, .25)\\ H_{0} : P \neq (.25, .25, .25, .25) \end{aligned}\]

10.1.3 Le test statistique d’ajustement

A ce stade, nous avons nos fréquences observées O et un ensemble de probabilités P correspondant à l’hypothèse nulle que nous voulons tester. Ce que nous voulons maintenant faire, c’est construire un test de l’hypothèse nulle. Comme toujours, si nous voulons tester H₀ contre H₁, nous allons avoir besoin d’une statistique de test. L’astuce de base d’un test d’adéquation consiste à construire une statistique de test qui mesure à quel point les données sont « proches » de l’hypothèse nulle. Si les données ne ressemblent pas à ce à quoi vous « vous attendriez » si l’hypothèse nulle était vraie, alors ce n’est probablement pas vrai. Bien, si l’hypothèse nulle est vraie, qu’est-ce qu’on s’attendrait à voir ? Ou, pour employer la terminologie correcte, quelles sont les fréquences attendues. Il y a N=200 observations, et (si l’hypothèse nulle est vraie) la probabilité que l’un d’eux choisisse un coeur est P₃=.25 , donc on peut supposer qu’on attend 200 X 0,25=50 cœurs. Ou, plus précisément, si nous laissons E_i référer au « nombre de réponses de catégorie i que nous attendons si l’hypothèse nulle est vraie », alors :

\[E_{i}=N\times P_{i}\]

S’il y a 200 observations qui peuvent être classées dans quatre catégories, et que nous pensons que les quatre catégories sont également probables, alors en moyenne nous nous attendrions à voir 50 observations dans chaque catégorie.

Maintenant, comment traduire cela en une statistique de test ? De toute évidence, ce que nous voulons faire, c’est comparer le nombre d’observations attendues dans chaque catégorie (E_i) avec le nombre d’observations observées dans cette catégorie (O_i). Puis sur la base de cette comparaison, nous devrions être en mesure d’établir une bonne statistique de test. Pour commencer, calculons la différence entre ce que nous attendions sous l’hypothèse nulle et ce que nous avons réellement trouvé. C’est-à-dire que nous calculons le score de différence « observé moins attendu », (O_i-E_i). Ceci est illustré dans le tableau suivant :

		Trèfle	Carreau	Coeur	Pique
fréquence prévue	Ei	50	50	50	50
fréquence observée	Oi	35	51	64	50
score de différence	Oi-Ei	15	-1	-14	0

D’après nos calculs, il est clair que les gens ont choisi plus de cœurs et moins de trèfles que ne le prévoyait l’hypothèse nulle. Cependant, un moment de réflexion suggère que ces différences brutes ne sont pas tout à fait ce que nous recherchons. Intuitivement, on a l’impression que c’est aussi mauvais quand l’hypothèse nulle prédit trop peu d’observations (ce qui est arrivé avec les cœurs) que quand elle prédit trop d’observations (ce qui est arrivé avec les trèfles). C’est donc un peu bizarre que nous ayons un nombre négatif pour les carreaux et un nombre positif pour les trèfles. Un moyen facile de résoudre ce problème est de tout élever au carré, de sorte que nous calculons maintenant les différences au carré, \((E_{i}-O{i})^{2}\). Comme auparavant, nous pouvons le faire à la main :

\((\text{observé} - \text{attendu})^2\)

Trèfle	Carreau	Cœur	Pique
225	1	196	0

Maintenant, nous faisons des progrès. Ce que nous avons maintenant, c’est une collection de chiffres qui sont gros quand l’hypothèse nulle fait une mauvaise prédiction (trèfles et cœurs), mais qui sont petits quand elle fait une bonne prédiction (carreaux et piques). Ensuite, pour des raisons techniques que j’expliquerai dans un instant, divisons aussi tous ces nombres par la fréquence Ei attendue, donc nous calculons actuellement \(\frac{\left( O_{i} - E_{i} \right)^{2}}{E_{i}}\). Depuis E_i=50 pour toutes les catégories dans notre exemple, ce n’est pas un calcul très intéressant, mais faisons-le quand même :

\((\text{observé} - \text{attendu})^2/\text{attendu}\)

Trèfle	Carreau	Cœur	Pique
4,5	0,02	3,92	0

En effet, nous avons ici quatre scores « d’écarts » différents, chacun d’eux nous indiquant l’ampleur de « l’erreur » que l’hypothèse nulle a faite lorsque nous avons essayé de l’utiliser pour prédire nos fréquences observées. Donc, afin de convertir ces données en une statistique de test utile, une chose que nous pourrions faire, c’est d’additionner ces chiffres. Le résultat s’appelle la statistique de la qualité de l’ajustement, conventionnellement appelée \(\chi^{2}\) (chi carré) ou Goodness of fit (GOF) en anglais. On peut le calculer comme suit :

\(\text{sum}((\text{observed} - \text{expected})^2 / \text{expected})\)

Cela nous donne une valeur de 8,44.

Si nous laissons \(k\) référer au nombre total de catégories (i.e. \(k = 4\) pour les données de nos cartes), alors la statistique \(\chi^{2}\) est donnée par :

\[ \chi^{2} = \sum_{i = 1}^{k}\frac{\left( O_{i} - E_{i} \right)^{2}}{E_{i}} \]

Intuitivement, il est clair que si \(\chi^{2}\) est petit, alors les données observées O_i sont très proches de ce que l’hypothèse nulle prédisait E_i, donc nous allons avoir besoin d’une grande statistique \(\chi^{2}\) afin de rejeter la nulle. Comme nous l’avons vu lors de nos calculs, dans notre jeu de données de cartes nous avons une valeur de \(\chi^{2}=8.44\). La question est donc maintenant de savoir si c’est une valeur assez grande pour rejeter l’hypothèse nulle.

10.1.4 La distribution d’échantillonnage de la statistique d’ajustement

Pour déterminer si une valeur particulière de \(\chi^{2}\) est suffisamment grande pour justifier le rejet de l’hypothèse nulle, nous devrons déterminer quelle serait la distribution d’échantillonnage pour \(\chi^{2}\) si l’hypothèse nulle est vraie. C’est donc ce que je vais faire dans cette section. Je vais vous montrer en détail comment cette distribution d’échantillonnage est construite, puis, dans la section suivante, l’utiliser pour construire un test d’hypothèse. Si vous voulez aller droit au but et que vous êtes prêt à croire que la distribution d’échantillonnage est une distribution \(\chi^{2}\) (chi carré) avec k-1 degrés de liberté, vous pouvez sauter le reste de cette section. Cependant, si vous voulez comprendre pourquoi le test d’ajustement fonctionne de cette façon, lisez ce qui suit.

Supposons que l’hypothèse nulle soit vraie. Si c’est le cas, la véritable probabilité qu’une observation tombe dans la i-ème catégorie est P_i. Après tout, c’est à peu près la définition de notre hypothèse nulle. Réfléchissons à ce que cela signifie vraiment. C’est un peu comme dire que c’est la « nature » qui décide si l’observation appartient ou non à la catégorie i en lançant une pièce pondérée (c’est-à-dire une pièce dont la probabilité de tomber sur face est P_j. Nous pouvons ainsi penser à notre fréquence O_j observée en imaginant que la nature a retourné N de ces pièces (une pour chaque observation dans l’ensemble de données), et exactement O_i d’entre elles sont tombées sur face. Évidemment, c’est une façon assez bizarre de penser à l’expérience. Mais le résultat (je l’espère), c’est vous rappeler que nous avons déjà vu ce scénario auparavant. C’est exactement la même configuration qui a donné lieu à la distribution binomiale de la Section 7.4. En d’autres termes, si l’hypothèse nulle est vraie, il s’ensuit que nos fréquences observées ont été générées par échantillonnage à partir d’une distribution binomiale :

\[O_{i}\sim Binomiale(P_{i},N)\]

Maintenant, si vous vous souvenez de notre discussion sur le théorème de la limite centrale (Section 8.3.3), la distribution binomiale commence à ressembler à peu près à la distribution normale, surtout quand N est grand et quand \(P_{i}\) n’est pas trop proche de 0 ou 1. En d’autres termes, tant que \(N \times P_{i}\) est assez grand. Ou, en d’autres termes, lorsque la O_i est normalement distribué alors c’est aussi le cas de \((O_{i} - E_{i})/\sqrt{E_{i}}\). Puisque \(E_{i}\) est une valeur fixe, soustraire E_i et diviser par \(\sqrt{E_{i}}\) change la moyenne et l’écart-type de la distribution normale, mais c’est tout. Voyons maintenant ce qu’est notre statistique d’ajustement. Ce que nous faisons, c’est prendre un ensemble de choses qui sont normalement distribuées, les mettre au carré et les additionner. Un instant ! On a déjà vu ça aussi ! Comme nous l’avons vu à la section 7.6, lorsque vous prenez une série de choses qui ont une distribution normale standard (c.-à-d. la moyenne 0 et l’écart-type 1), que vous les élevez au carré puis que vous les additionnez, la quantité résultante a une distribution de chi carré. Nous savons maintenant que l’hypothèse nulle prédit que la distribution d’échantillonnage de la statistique d’ajustement est une distribution du chi carré. Cool.

Il y a un dernier détail dont il faut parler, à savoir les degrés de liberté. Si vous vous souvenez de la section 7.6, j’ai dit que si le nombre de valeurs que vous additionnez est k, alors les degrés de liberté pour la distribution du chi carré résultante sont k. Pourtant, ce que j’ai dit au début de cette section est que les degrés de liberté réels pour le test d’ajustement du chi carré sont k - 1. Pourquoi ? La réponse ici est que ce que nous sommes censés examiner, c’est le nombre de valeur vraiment indépendantes qui s’additionnent. Et, comme je vais continuer à en parler dans la section suivante, même s’il y a k valeurs que nous ajoutons seulement k- 1 d’entre elles sont vraiment indépendantes, et donc les degrés de liberté sont en fait seulement k-1. C’est le sujet de la section suivante.⁶⁸

10.1.5 Degrés de liberté

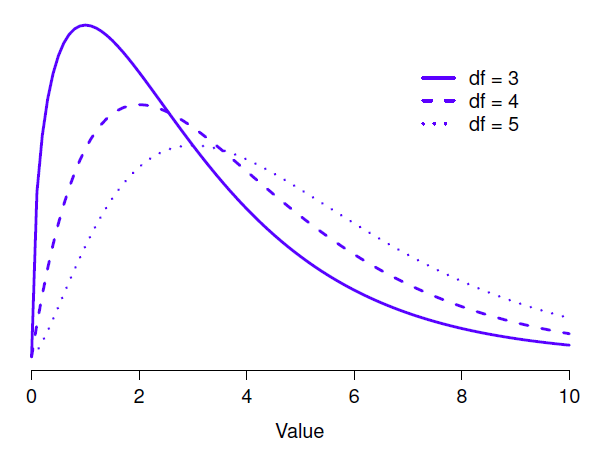
Figure 10‑1 : distributions \(\chi^{2}\) (chi-carré) pour les différentes valeurs des « degrés de liberté ».

Lorsque j’ai introduit la distribution du khi-carré dans la section 7.6, j’étais un peu vague sur ce que signifient réellement les « degrés de liberté ». De toute évidence, c’est important. En regardant la Figure 10‑1, vous pouvez voir que si nous changeons les degrés de liberté, alors la distribution du chi carré change de forme de façon assez substantielle. Mais qu’est-ce que c’est exactement ? Encore une fois, quand j’ai présenté la distribution et expliqué sa relation avec la distribution normale, j’ai offert une réponse : c’est le nombre de « valeurs normalement distribuées » que j’élève au carré et que j’additionne. Mais, pour la plupart des gens, c’est un peu abstrait et pas tout à fait utile. Ce que nous devons vraiment faire, c’est essayer de comprendre les degrés de liberté en termes de données. Alors c’est parti.

L’idée de base derrière les degrés de liberté est assez simple. Vous le calculez en comptant le nombre de « quantités » distinctes utilisées pour décrire vos données et en soustrayant ensuite toutes les « contraintes » que ces données doivent satisfaire.⁶⁹ C’est un peu vague, alors utilisons les données de nos cartes comme exemple concret. Nous décrivons nos données à l’aide de quatre chiffres, O₁, O₂, O₃ et O₄ correspondant aux fréquences observées dans les quatre catégories différentes (cœurs, trèfles, carreaux, piques). Ces quatre chiffres sont les résultats aléatoires de notre expérience. Mais mon expérience comporte en fait une contrainte fixe : la taille de l’échantillon N.⁷⁰ C’est-à-dire que si nous savons combien de personnes ont choisi des cœurs, combien ont choisi des carreaux et combien ont choisi des trèfles, alors nous serons en mesure de déterminer exactement combien ont choisi des piques. En d’autres termes, bien que nos données soient décrites à l’aide de quatre chiffres, elles ne correspondent en fait qu’à 4 - 1 = 3 degrés de liberté. Une façon légèrement différente d’y penser est de remarquer qu’il y a quatre probabilités qui nous intéressent (encore une fois, correspondant aux quatre catégories différentes), mais ces probabilités doivent s’additionner en une, ce qui impose une contrainte. Les degrés de liberté sont donc 4 - 1 = 3. Qu’on veuille y penser en termes de fréquences observées ou en termes de probabilités, la réponse est la même. En général, lorsque l’on effectue le test d’adéquation \(\chi^{2}\) (chi carré) pour une expérience impliquant k groupes, les degrés de liberté seront k- 1.

10.1.6 Vérification de l’hypothèse nulle

L’étape finale dans le processus de construction de notre test d’hypothèse est de déterminer ce qu’est la région de rejet. C’est-à-dire, quelles valeurs de \(\chi^{2}\) nous amèneraient à rejeter l’hypothèse nulle. Comme nous l’avons vu précédemment, les grandes valeurs de \(\chi^{2}\) impliquent que l’hypothèse nulle a mal prédit les données de notre expérience, alors que les petites valeurs de \(\chi^{2}\) impliquent qu’elle est en fait assez bien faite. Par conséquent, une stratégie assez raisonnable serait de dire qu’il y a une valeur critique telle que si \(\chi^{2}\) est supérieur à la valeur critique, nous rejetons l’hypothèse nulle, mais si \(\chi^{2}\) est inférieur à cette valeur, nous conservons la valeur nulle. En d’autres termes, pour reprendre les termes que nous avons utilisés au chapitre 9, le test du chi carré est toujours un test unilatéral. Tout ce qu’on a à faire, c’est de trouver quelle est cette valeur critique. Et c’est assez simple. Si nous voulons que notre test ait un niveau de signification de \(\alpha =.05\) (c’est-à-dire que nous sommes prêts à tolérer un taux d’erreur de type I de 5 %), alors nous devons choisir notre valeur critique de sorte qu’il n’y ait que 5 % de chances que \(\chi^{2}\) soit aussi grand si l’hypothèse nulle est vraie. C’est ce qu’illustre la Figure 10‑2.

Vous vous demandez, comment puis-je trouver la valeur critique d’une distribution du chi carré avec k-1 degrés de liberté ? Il y a de nombreuses années, lorsque j’ai suivi pour la première fois un cours de psychologie statistique, nous avions l’habitude de rechercher ces valeurs critiques dans un livre de tableaux des valeurs critiques, comme celui de la Figure 10‑3. En regardant cette figure, nous pouvons voir que la valeur critique pour une distribution \(\chi^{2}\) avec 3 degrés de et p=.05 est 7,815.

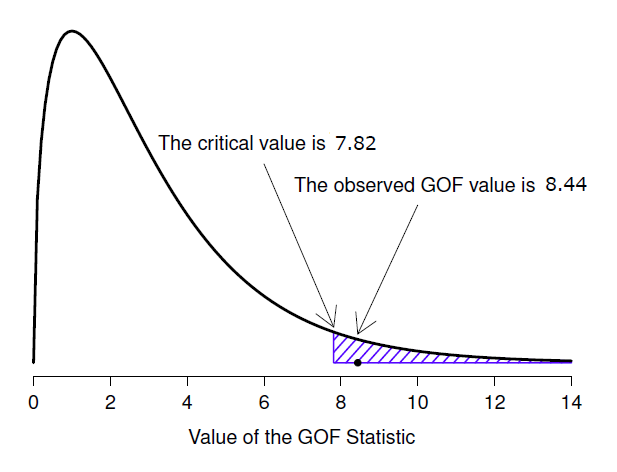
Figure 10‑2 : Illustration du fonctionnement du test d’hypothèse pour le test d’ajustement (Goodness of fit)\(\chi^{2}\) (chi carré).

Ainsi, si notre statistique calculée \(\chi^{2}\) est supérieure à la valeur critique de 7,815, alors nous pouvons rejeter l’hypothèse nulle (souvenez-vous que l’hypothèse nulle, K₀, est que les quatre couleurs sont choisies avec une probabilité égale). Puisque nous avons déjà calculé qu’avant (i.e., \(\chi^{2}=8.44\)) nous pouvons rejeter l’hypothèse nulle. Et c’est tout, en gros. Vous connaissez maintenant le « test d’ajustement de Pearson \(\chi^{2}\) ». Vous avez de la chance.

10.1.7 Faire le test dans Jamovi

Comme il fallait s’y attendre, Jamovi fournit une analyse qui fera ces calculs pour vous. Dans la barre d’outils principale « Analyses », sélectionnez « Frequencies » - « One Sample Proportion Tests » - « N outcomes ». Ensuite, dans la fenêtre d’analyse qui apparaît, déplacez la variable que vous voulez analyser (choix 1 dans la case « Variable »). Puis, cliquez sur la case à cocher « Expected counts » (effectifs attendus) pour qu’ils soient affichés dans le tableau des résultats. Lorsque vous avez fait tout cela, vous devriez voir les résultats de l’analyse dans Jamovi comme dans la Figure 10‑4. Il n’est pas surprenant que Jamovi fournisse les mêmes chiffres et statistiques que ceux que nous avons calculés à la main ci-dessus, avec une valeur de 8,44 sur \(\chi^{2}\) avec 3 df⁷¹ et p=0,038. Notez que nous n’avons plus besoin de chercher une valeur seuil critique de p-value, car Jamovi donne la valeur p réelle du \(\chi^{2}\) calculé pour 3 df.

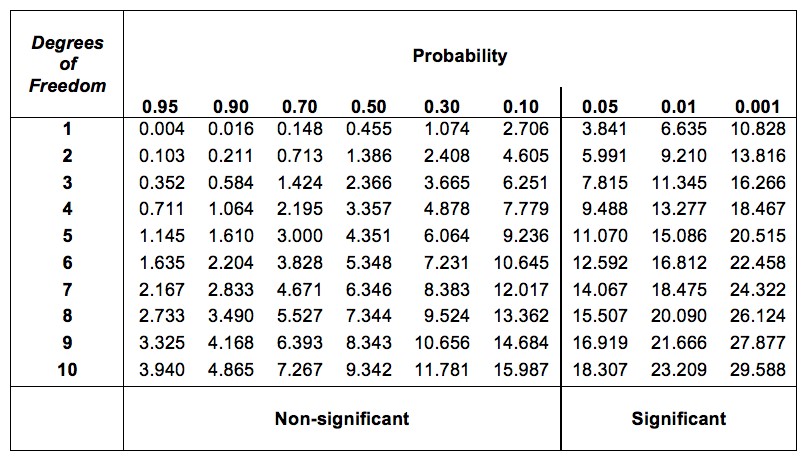
Figure 10‑3 : Tableau des valeurs critiques pour la distribution du chi carré

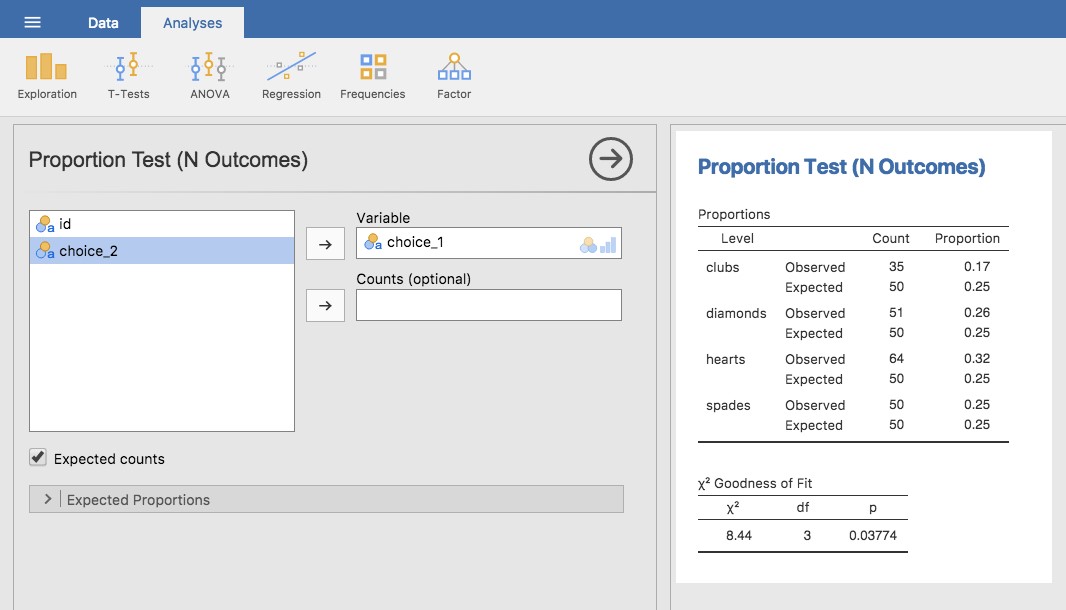
Figure 10‑4 : Un test d’ajustement unilatéral \(\chi^{2}\) (One Sample Proportion Test) dans Jamovi, avec tableau montrant les fréquences et proportions observées et attendues.

10.1.8 Spécification d’une hypothèse nulle différente

À ce stade, vous vous demandez peut-être ce qu’il faut faire si vous voulez faire un test d’adéquation, mais votre hypothèse nulle n’est pas que toutes les catégories sont également probables. Supposons, par exemple, que quelqu’un ait prédit théoriquement que les gens devraient choisir des cartes rouges 60 % du temps, et des cartes noirs 40 % du temps (je ne sais pas pourquoi vous auriez prédit cela), mais qu’il n’avait aucune autre préférence. Si tel était le cas, l’hypothèse nulle serait de s’attendre à ce que 30% des choix soient des cœurs, 30% des carreaux, 20% des piques et 20% des trèfles. En d’autres termes, on s’attendrait à ce que les cœurs et les carreaux apparaissent 1,5 fois plus souvent que les piques et les trèfles (le ratio 30% :20% est le même que 1,5 :1). Cela me semble être une théorie idiote et il est assez facile de tester cette hypothèse nulle explicitement spécifiée avec les données de notre analyse Jamovi. Dans la fenêtre d’analyse (intitulée « Proportion Test (N Outcomes) » présentée dans la Figure 10‑4, vous pouvez développer les options pour « Expected proportions ». Pour ce faire, vous avez la possibilité de saisir différentes valeurs de ratio pour la variable que vous avez sélectionnée, dans notre cas, il s’agit du choix 1. Modifiez le ratio pour tenir compte de la nouvelle hypothèse nulle, comme dans la Figure 10‑5, et voyez comment les résultats changent et la statistique \(\chi^{2}\) est de 4,74, 3 df., p = 0,182.

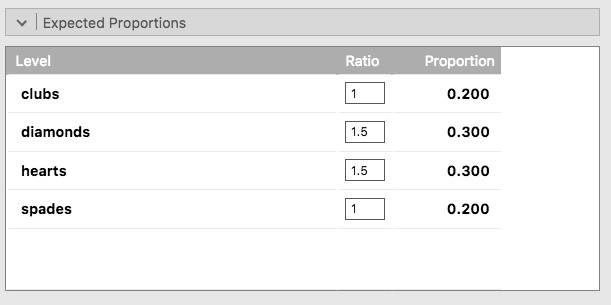
Figure 10‑5 : Changement des proportions attendues dans le test de la proportion d’un échantillon dans Jamovi (\(\chi^{2}\) One Sample Proportion)

Les nombres attendus sont maintenant :

		Trèfle	Carreau	Coeur	Pique
fréquence prévue	Ei	40	60	40	60

Maintenant, les résultats de nos hypothèses mises à jour et les fréquences attendues sont différentes de ce qu’elles étaient la dernière fois. En conséquence, notre statistique de test \(\chi^{2}\) est différente, et notre valeur p est également différente. Malheureusement, la valeur p est de 0,182, nous ne pouvons donc pas rejeter l’hypothèse nulle (reportez-vous à la section 9.5 pour vous rappeler pourquoi). Malheureusement, malgré le fait que l’hypothèse nulle corresponde à une théorie très stupide, ces données ne fournissent pas suffisamment de preuves contre elle.

10.1.9 Comment rapporter les résultats du test

Maintenant vous savez comment le test fonctionne, et vous savez comment faire le test à l’aide d’une merveilleuse baguette magique Jamovi. La prochaine chose que vous devez savoir, c’est comment rédiger les résultats. Après tout, il ne sert à rien de concevoir et de réaliser une expérience, puis d’analyser les données si vous n’en parlez à personne ! Parlons maintenant de ce que vous devez faire lorsque vous présentez votre analyse. Restons-en à l’exemple de nos combinaisons. Si je voulais écrire ce résultat pour un article ou quelque chose comme ça, alors la façon conventionnelle de le rapporter serait d’écrire quelque chose comme ceci :

Sur les 200 participants à l’expérience, 64 ont sélectionné des cœurs pour leur premier choix, 51 ont sélectionné des carreaux, 50 des piques et 35 des trèfles. Un test d’ajustement du chi carré a été effectué pour vérifier si les probabilités de choix étaient identiques pour les quatre couleurs. Les résultats ont été significatifs (\(\chi^{2}(3)=8.44, p<.05\)), ce qui suggère que les gens n’ont pas choisi les couleurs au hasard.

C’est assez simple et, espérons-le, cela semble assez banal. Cela dit, il y a certaines choses que vous devriez noter au sujet de cette description :

• Le test statistique est précédé des statistiques descriptives. C’est-à-dire, j’ai dit au lecteur à quoi ressemblaient les données avant de faire le test. En général, il s’agit d’une bonne pratique. Rappelez-vous toujours que votre lecteur ne connaît pas vos données aussi bien que vous. Donc, à moins que vous ne le leur décriviez correctement, les tests statistiques n’auront aucun sens pour eux et ils en seront frustrés et tristes.
• La description vous indique quelle est l’hypothèse nulle testée. Pour être honnête, les rédacteurs ne le font pas toujours, mais c’est souvent une bonne idée dans les situations où il existe une certaine ambiguïté ou lorsque vous ne pouvez pas compter sur le fait que vos lecteurs connaissent bien les outils statistiques que vous utilisez. Très souvent, le lecteur ne connaît pas (ou ne se souvient pas) de tous les détails du test que vous utilisez, c’est donc une sorte de politesse de leur « rappeler » ! En ce qui concerne le test d’adéquation, vous pouvez généralement compter sur un public scientifique qui sait comment il fonctionne (puisqu’il est couvert dans la plupart des cours d’introduction aux statistiques). Cependant, c’est quand même une bonne idée d’être explicite sur l’énoncé de l’hypothèse nulle (brièvement !) parce que l’hypothèse nulle peut être différente en fonction de l’objectif vous conduisant à utiliser le test. Dans l’exemple des cartes, mon hypothèse nulle était que les quatre probabilités des couleurs étaient identiques (c.-à-d. P₁=P₂=P₄=P₄=0,25), mais il n’y a rien de spécial dans cette hypothèse. J’aurais tout aussi bien pu tester l’hypothèse nulle que P₁=0,7 et P₂=P₃=P₄= 0,1 en utilisant un test d’adéquation. Il est donc utile pour le lecteur que vous lui expliquiez quelle était votre hypothèse nulle. Notez aussi que j’ai décrit l’hypothèse nulle avec des mots, pas avec des maths. C’est parfaitement acceptable. Vous pouvez la décrire en termes mathématiques si vous le souhaitez, mais comme la plupart des lecteurs trouvent les mots plus faciles à lire que les symboles, la plupart des auteurs ont tendance à décrire l’hypothèse nulle en utilisant des mots s’ils le peuvent.
• Un « bloc statistique » est inclus. En rapportant les résultats du test lui-même, je n’ai pas seulement dit que le résultat était significatif, j’ai inclus un « bloc statistique » (c’est-à-dire la partie mathématique dense entre parenthèses) qui rapporte toutes les informations statistiques « clés ». Pour le test d’ajustement du chi carré, l’information qui est rapportée est la statistique de test (que la statistique d’ajustement était de 8,44), l’information sur la distribution utilisée dans le test (\(\chi^{2}\) avec 3 degrés de liberté qui est habituellement raccourci à \(\chi_{(3)}^{2}\), et ensuite la décision à savoir si le résultat est significatif (dans ce cas p<.05). L’information particulière qui doit entrer dans le bloc statistique est différente pour chaque test, et chaque fois que je présente un nouveau test, je vous montre à quoi doit ressembler le bloc statistique.⁷² Cependant, le principe général est que vous devriez toujours fournir suffisamment d’informations pour que le lecteur puisse vérifier lui-même les résultats du test s’il le souhaite vraiment.
• Les résultats sont interprétés. En plus d’indiquer que le résultat était significatif, j’ai fourni une interprétation du résultat (c.-à-d. que les gens n’ont pas choisi au hasard). C’est aussi une politesse envers le lecteur, parce que cela lui dit quelque chose sur ce qu’il doit croire de ce qui se passe dans vos données. Si vous n’incluez pas quelque chose comme ça, c’est vraiment difficile pour votre lecteur de comprendre ce qui se passe.⁷³

Comme pour tout le reste, votre souci premier devrait être d’expliquer les choses à votre lecteur. Rappelez-vous toujours que le but de rapporter vos résultats est de communiquer à un autre être humain. Je ne peux pas vous dire combien de fois j’ai vu la section des résultats d’un rapport, d’une thèse ou même d’un article scientifique qui n’est que du charabia, parce que l’auteur s’est concentré uniquement sur le fait d’avoir inclus tous les chiffres et oublié de communiquer avec le lecteur humain.

10.1.10 Un commentaire sur la notation statistique

Satan se plaît aussi bien dans les statistiques que dans la citation des Écritures. - H.G. Wells

Si vous avez lu très attentivement, et que vous êtes autant un pédant mathématique que moi, il y a une chose dans la façon dont j’ai écrit le test du chi carré dans la dernière section qui pourrait vous déranger un peu. vous vous dites peut-être : il y a quelque chose qui ne va pas du tout avec le fait d’écrire « \(\chi^{2}(3)=8.44\),. Après tout, c’est la statistique de la qualité de l’ajustement qui est égale à 8,44, alors n’aurais-je pas dû écrire \(X^{2}=8.44\) ou peut-être \(\text{GOF}=8.44\) ? Cela semble confondre la distribution d’échantillonnage (c.-à-d. \(\chi^{2}\) avec df = 3) avec la statistique du test (c.-à-d. \(X^{2}\)). Il y a fort à parier que vous pensiez qu’il s’agissait d’une faute de frappe, puisque \(\chi\) et X se ressemblent beaucoup. Curieusement, ça ne l’est pas. Ecrire \(\chi^{2}(3)=8.44\) est essentiellement une façon très condensée d’écrire «la distribution d’échantillonnage de la statistique du test est \(\chi^{2}(3)\), et la valeur de la statistique du test est 8,44».

Dans un sens, c’est un peu stupide. Il existe de nombreuses statistiques de test différentes qui s’avèrent avoir une distribution d’échantillonnage du chi carré. La statistique \(\chi^{2}\) que nous avons utilisée pour notre test d’ajustement n’est qu’une statistique parmi tant d’autres (bien qu’elle soit l’une des plus fréquemment rencontrées). Dans un monde sensible et parfaitement organisé, nous aurions toujours un nom distinct pour la statistique du test et la distribution d’échantillonnage. De cette façon, le bloc de statistiques lui-même vous dirait exactement ce que le chercheur a calculé. Parfois, ça arrive. Par exemple, la statistique de test utilisée dans le test d’ajustement de Pearson s’écrit \(\chi^{2}\), mais il existe un test étroitement lié connu sous le nom de test G⁷⁴ (Sokal et Rohlf 1994), dans lequel la statistique de test s’écrit G. En l’occurrence, le test d’ajustement de Pearson et le test G testent la même hypothèse nulle et la distribution de l’échantillonnage est exactement la même (c’est-à-dire chi carré avec k -1 degrés de liberté). Si j’avais fait un test G pour les données des cartes plutôt qu’un test d’ajustement, alors j’aurais obtenu une statistique de test de G = 8.65, qui est légèrement différente de la valeur \(\chi^{2}=8,44\) que j’ai obtenue plus tôt et qui produit une valeur p légèrement inférieure de p=.034. Supposons que la convention consiste à déclarer la statistique du test, puis la distribution d’échantillonnage, et enfin la valeur p. Si c’était vrai, alors ces deux situations produiraient des blocs statistiques différents : mon résultat original serait écrit \(X^{2}=8.44, \chi^{2}(3), p=.038\), alors que la nouvelle version utilisant le test G serait écrite \(G=8.65, \chi^{2}(3), p=.034\). Cependant, en utilisant la norme d’écriture condensée, le résultat original est écrit \(\chi^{2}(3)=8.44, p=.038\), et le nouveau est écrit \(\chi^{2}(3)=8.65, p=.034\), et savoir quel test j’ai fait n’est pas clair.

Alors pourquoi ne vivons-nous pas dans un monde dans lequel le contenu du bloc de statistiques spécifie de façon unique quels tests ont été effectués ? La raison profonde est que la vie est désordonnée. Nous (en tant qu’utilisateurs d’outils statistiques) voulons qu’il soit agréable, propre et organisé. Nous voulons qu’il soit conçu comme s’il s’agissait d’un produit, mais ce n’est pas ainsi que la vie fonctionne. La statistique est une discipline intellectuelle comme une autre, et en tant que telle, c’est un projet massivement distribué, partiellement collaboratif et partiellement compétitif que personne ne comprend vraiment complètement. Les choses que vous et moi utilisons comme outils d’analyse de données n’ont pas été créées par une loi des dieux de la statistique. Ils ont été inventés par beaucoup de personnes différentes, publiés sous forme d’articles dans des revues universitaires, mis en œuvre, corrigés et modifiés par beaucoup d’autres personnes, puis expliqués aux étudiants dans des manuels scolaires par quelqu’un d’autre. Par conséquent, il y a beaucoup de statistiques de test qui n’ont même pas de noms, et par conséquent, on leur donne juste le même nom que la distribution d’échantillonnage correspondante. Comme nous le verrons plus loin, toute statistique de test qui suit une distribution \(\chi^{2}\) est communément appelée « statistique du chi carré », tout ce qui suit une distribution t est appelé « statistique t », et ainsi de suite. Mais, comme l’illustre l’exemple de \(\chi^{2}\) par rapport à G, deux choses différentes avec la même distribution d’échantillonnage sont toujours … différentes.

Par conséquent, c’est parfois une bonne idée d’être clair sur le test que vous avez effectué, surtout si vous faites quelque chose d’inhabituel. Si vous dites simplement « test du chi carré », on ne sait pas vraiment de quel test vous parlez. Bien que, puisque les deux tests du chi carré les plus courants sont le test d’ajustement et le test d’indépendance (section 10.2), la plupart des lecteurs ayant une formation en statistiques peuvent probablement deviner. Néanmoins, c’est quelque chose dont il faut être conscient.

10.2 Le test d’indépendance (ou d’association) \(\chi^{2}\)

GUARDBOT 1 : Halte ! GUARDBOT 2 : Etes-vous robot ou humain ? LEELA : Nous sommes robot. FRY : Euh, ouais ! Juste deux robots en train de le voler ! Hein ? GUARDBOT 1: Administrer le test. GUARDBOT 2: Lequel des énoncés suivants préféreriez-vous le plus ?

A : Un chiot, B : Une jolie fleur pour votre chéri, ou C : Un gros fichier de données correctement formaté ?

GUARDBOT 1 : Choisissez ! /- Futurama, «Fear of a Bot Planet»

L’autre jour, je regardais un documentaire animé examinant les coutumes pittoresques des indigènes de la planète Chapek 9. Apparemment, pour avoir accès à leur capitale, un visiteur doit prouver qu’il est un robot, pas un humain. Afin de déterminer si un visiteur est humain ou non, les autochtones lui demandent s’il préfère des chiots, des fleurs ou de gros fichiers de données correctement formatés. « Plutôt malin, me suis-je dit, et si les humains et les robots avaient les mêmes préférences ? Ce ne serait alors probablement pas un très bon test » Il se trouve que j’ai mis la main sur les données de test que les autorités civiles de Chapek 9 utilisaient pour vérifier cela. Il s’avère que ce qu’ils ont fait était très simple. Ils ont trouvé un tas de robots et un tas d’humains et leur ont demandé ce qu’ils préféraient. J’ai sauvegardé leurs données dans un fichier appelé chapek9.omv, que nous pouvons maintenant charger dans Jamovi. En plus de la variable ID qui identifie les individus, il y a deux variables nominales, l’espèce et le choix. Au total, il y a 180 entrées dans l’ensemble de données, une pour chaque personne (en comptant à la fois les robots et les humains comme « personnes ») à qui on a demandé de faire un choix. Plus précisément, il y a 93 humains et 87 robots, et le fichier de données est de loin le meilleur choix. Vous pouvez le vérifier vous-même en demandant à Jamovi des tableaux de fréquences, sous le bouton « Exploration » - « Descriptives ». Cependant, ce résumé ne répond pas à la question qui nous intéresse. Pour ce faire, nous avons besoin d’une description plus détaillée des données. Ce que nous voulons faire, c’est examiner les choix ventilés par espèce. En d’autres termes, nous devons croiser les données (voir la section 6.1). Dans Jamovi, nous le faisons en utilisant l’analyse « Fréquencies » - « Contingency Tables » - « Independants Samples », et nous devrions obtenir un tableau comme celui-ci :

	Robot	Humain	Total
Chiot	13	15	28
Fleur	30	13	43
Données	44	65	109
Total	87	93	180

Il en ressort clairement que la grande majorité des humains ont choisi le fichier de données, alors que les robots avaient tendance à être beaucoup plus équilibrés dans leurs préférences. En laissant de côté la question de savoir pourquoi les humains seraient plus susceptibles de choisir le fichier de données pour le moment (ce qui semble assez étrange, il est vrai), notre première tâche consiste à déterminer si l’écart entre les choix humains et les choix robotiques dans l’ensemble de données est statistiquement significatif.

10.2.1 Construire notre test d’hypothèse

Comment analyser ces données ? Plus précisément, puisque mon hypothèse de recherche est que « les humains et les robots répondent à la question de façon différente », comment puis-je construire un test de l’hypothèse nulle selon laquelle « les humains et les robots répondent à la question de la même façon » ? Comme précédemment, nous commençons par établir une notation pour décrire les données :

	Robot	Humain	Total
Chiot	O11	O12	R1
Fleur	O21	O22	R2
Données	O31	O32	R3
Total	C1	C2	N

Dans cette notation, nous disons que O_i est un comptage (fréquence observée) du nombre de répondants de l’espèce j (robots ou humains) qui ont donné la réponse i (chiot, fleur ou données) quand on leur a demandé de faire un choix. Le nombre total d’observations est écrit N, comme d’habitude. Enfin, j’ai utilisé R_i pour indiquer les totaux des lignes (par exemple, R₁ est le nombre total de personnes qui ont choisi la fleur), et C_j pour indiquer les totaux des colonnes (par exemple, C₁ est le nombre total de robots).⁷⁵

Réfléchissons maintenant à ce que dit l’hypothèse nulle. Si les robots et les humains répondent de la même manière à la question, cela signifie que la probabilité « qu’un robot choisisse chiot » est la même que la probabilité « qu’un humain choisisse chiot », et ainsi de suite pour les deux autres possibilités. Donc, si nous utilisons P_ij pour indiquer « la probabilité qu’un membre de l’espèce j donne la réponse i» alors notre hypothèse nulle est que : H₀: Toutes les affirmations suivantes sont vraies : P₁₁=P₁₂(même probabilité de dire «chiot») P₂₁=P₂₂ (même probabilité de dire «fleur») et P₃₁=P₃₂(même probabilité de dire «données»)

En fait, puisque l’hypothèse nulle prétend que les probabilités de choix réelles ne dépendent pas de l’espèce de la personne qui fait le choix, nous pouvons laisser P_i se référer à cette probabilité, par exemple, P₁ est la probabilité réelle de choisir le chiot.

Ensuite, de la même façon que nous l’avons fait avec le test de la qualité d’ajustement, nous devons calculer les fréquences attendues. En d’autres termes, pour chacun des effectifs O_ij observés, nous devons déterminer ce à quoi nous attendre avec l’hypothèse nulle. Notons cette fréquence attendue par E_ij. Cette fois, c’est un peu plus délicat. S’il y a un total de personnes C_j qui appartiennent à l’espèce j, et que la vraie probabilité pour quiconque (indépendamment de l’espèce) de choisir l’option i est P_i, alors la fréquence prévue est juste :

\[ E_{ij} = C_{j}\times P_{i} \]

Tout cela est très bien, mais nous avons un problème. Contrairement à la situation que nous avons eue avec le test d’adéquation, l’hypothèse nulle ne spécifie pas réellement une valeur particulière pour P_i. C’est quelque chose que nous devons estimer (chapitre 8) à partir des données ! Heureusement, c’est assez facile à faire. Si 28 personnes sur 180 ont sélectionné les fleurs, alors une estimation naturelle de la probabilité de choisir des fleurs est 28/180, ce qui représente environ .16. Si nous formulons cela en termes mathématiques, ce que nous disons, c’est que notre estimation de la probabilité de choisir l’option i n’est que le total des lignes divisé par la taille totale de l’échantillon :

\[ \hat{P_{i}} = \frac{R_{i}}{N} \]

Par conséquent, notre fréquence prévue peut s’écrire comme le produit (c.-à-d. la multiplication) du total des lignes et du total des colonnes, divisé par le nombre total d’observations :⁷⁶

\[ E_{{ij}} = \frac{R_{i}\times C_{j}}{N} \]

Maintenant que nous avons trouvé comment calculer les fréquences attendues, il est simple de définir une statistique de test, suivant exactement la même stratégie que celle que nous avons utilisée dans le test d’ajustement. En fait, c’est à peu près la même statistique.

Pour un tableau de contingence avec r lignes et c colonnes, l’équation qui définit notre statistique \(\chi^{2}\) est la suivante

\[ \chi^{2} = \sum_{i = 1}^{r}{\sum_{j = 1}^{c}\frac{\left( E_{{ij}} - O_{{ij}} \right)^{2}}{E_{{ij}}}} \]

La seule différence est que je dois inclure deux signes de sommation (i.e., \(\sum\)) pour indiquer que nous faisons la somme sur les lignes et colonnes.

Comme précédemment, les grandes valeurs de \(\chi^{2}\) indiquent que l’hypothèse nulle fournit une mauvaise description des données, alors que les petites valeurs de \(\chi^{2}\) suggèrent qu’elle rend bien compte des données. Par conséquent, comme la dernière fois, nous cherchons à rejeter l’hypothèse nulle si \(\chi^{2}\) est trop grand.

Comme on pouvait s’y attendre, cette statistique est distribuée comme \(\chi^{2}\) Tout ce que nous avons à faire est de déterminer combien de degrés de liberté sont impliqués, ce qui n’est pas trop difficile. Comme je l’ai déjà mentionné, vous pouvez (habituellement) penser que les degrés de liberté sont égaux au nombre de données que vous analysez, moins le nombre de contraintes. Un tableau de contingence avec r lignes et c colonnes contient un total de \(r \times c\) fréquences observées, donc c’est le nombre total d’observations. Qu’en est-il des contraintes ? Ici, c’est un peu plus délicat. La réponse est toujours la même mais l’explication de la raison pour laquelle les degrés de liberté prennent cette valeur est différente selon le plan expérimental.

\[ df = \left( C - 1 \right)\times(R - 1) \]

Supposons que nous avions honnêtement l’intention de sonder exactement 87 robots et 93 humains (totaux de colonnes fixés par l’expérimentateur), mais que nous avons laissé les totaux de lignes libres de varier (les totaux de lignes sont des variables aléatoires). Pensons aux contraintes qui s’appliquent ici. Eh bien, puisque nous avons délibérément fixé les totaux des colonnes par action de l’expérimentateur, nous avons c contraintes dans ce cas-là. Mais, en fait, il y a plus que ça. Rappelez-vous comment notre hypothèse nulle avait des paramètres libres (c.-à-d. que nous devions estimer les valeurs P_i) ? Celles-ci comptent aussi. Je n’expliquerai pas pourquoi dans ce livre, mais chaque paramètre libre dans l’hypothèse nulle est un peu comme une contrainte supplémentaire. Alors, combien sont-ils ? Eh bien, puisque ces probabilités doivent s’additionner à 1, il n’y en a que r-1. Donc notre degré total de liberté est :

\[ \begin{aligned} df & = (\text{nombre d'observations}- \text{nombre de contraintes})\\ & =(rc)-(c+r-1))\\ & = rc-c-r+1\\ & = (r-1)(c-1) \end{aligned} \]

Autrement dit, nous avons interrogé les 180 premières personnes que nous avons vues et il s’est avéré que 87 étaient des robots et 93 étaient des humains. Cette fois-ci, notre raisonnement serait légèrement différent, mais nous conduirait quand même à la même réponse. Notre hypothèse nulle a toujours r-1 paramètres libres correspondant aux probabilités de choix, mais elle a maintenant c - 1 paramètres libres correspondant aux probabilités d’espèces, car il faudrait aussi estimer la probabilité qu’une personne échantillonnée au hasard se révèle être un robot.⁷⁷ Enfin, puisque nous avons effectivement fixé le nombre total d’observations N, c’est une contrainte de plus. Nous avons donc maintenant des observations rc et des contraintes (c-1)+(r-1)+1. Qu’est-ce que ça donne ?

\[ \begin{aligned} df & = (\text{nombre d'observations}- \text{nombre de contraintes})\\ & =rc-((c-1)+(r-1)+1\\ & = rc-c-r+1\\ & = (r-1)(c-1) \end{aligned} \]

Incroyable !

10.2.2 Faire le test avec Jamovi

Maintenant qu’on sait comment fonctionne le test, voyons comment ça se passe en Jamovi. Aussi tentant que cela puisse paraître de vous guider à travers les calculs fastidieux pour que vous soyez forcé de l’apprendre sur le long terme, je me dis que cela n’a pas de sens. Je vous ai déjà montré comment le faire sur le long chemin pour le test d’adéquation dans la dernière section, et comme le test d’indépendance n’est pas différent sur le plan conceptuel, vous n’apprendrez rien de nouveau en le faisant à la main. Alors à la place, je vais vous montrer le chemin le plus facile. Après avoir effectué le test dans Jamovi (« Frequencies » -« Contingency Tables » -« Independent Samples »), tout ce que vous avez à faire est de regarder sous le tableau de contingence dans la fenêtre de résultats Jamovi, il y a la statistique \(\chi^{2}\) pour vous. Ceci montre une valeur statistique de \(\chi^{2}\) de 10.72, avec 2 df. et p-value = 0,005.

C’était facile, n’est-ce pas ? Vous pouvez également demander à Jamovi de vous montrer les effectifs attendus - il vous suffit de cliquer sur la case à cocher « Counts » - « Expected » dans les options « cells » et les effectifs attendus apparaîtront dans le tableau de contingence. Pendant que vous faites cela, une mesure de la taille de l’effet serait utile. Nous choisirons Cramer’s V, et vous pouvez le spécifier à partir d’une case à cocher dans les options « Statistiques », et cela donne une valeur pour Cramer’s V de 0,24. Nous en reparlerons dans un instant.

Ce résultat nous donne suffisamment d’informations pour rédiger le résultat :

Le \(\chi^{2}\) de Pearson révèle une association significative entre les espèces et le choix \(\chi^{2}(2) = 10,7, p<.01\)). Les robots semblaient plus portés à dire qu’ils préféraient les fleurs, alors que les humains étaient plus portés à dire qu’ils préféraient les données.

Remarquez qu’une fois de plus, j’ai fourni un peu d’interprétation pour aider le lecteur humain à comprendre ce qui se passe avec les données. Plus tard dans ma section de discussion, je préciserai un peu plus le contexte. Pour illustrer la différence, voici ce que je dirai probablement plus tard :

Le fait que les humains semblaient avoir une préférence plus marquée pour les fichiers de données brutes que les robots est quelque peu contre-intuitif. Cependant, dans le contexte, cela a un certain sens, car l’autorité civile sur Chapek 9 a une tendance malheureuse à tuer et à disséquer les humains lorsqu’ils sont identifiés. Il semble donc très probable que les participants humains n’aient pas répondu honnêtement à la question, afin d’éviter des conséquences potentiellement indésirables. Il s’agit là d’une faiblesse méthodologique importante.

Je suppose que cela pourrait être considéré comme un exemple assez extrême d’effet de réactivité. De toute évidence, dans ce cas, le problème est suffisamment grave pour que l’étude soit plus ou moins inutile en tant qu’outil permettant de comprendre la différence entre les préférences des humains et des robots. Cependant, j’espère que cela illustre la différence entre obtenir un résultat statistiquement significatif (notre hypothèse nulle est rejetée en faveur de l’alternative), et trouver quelque chose de valeur scientifique (les données ne nous disent rien d’intéressant sur notre hypothèse de recherche en raison d’un grand défaut méthodologique).

10.2.3 Postscript

Plus tard, j’ai découvert que les données avaient été inventées et que j’avais regardé des dessins animés au lieu de travailler.

10.3 La correction de continuité

Bien, c’est l’heure d’une petite digression. Je vous ai un peu menti jusqu’ici. Il y a un petit changement que vous devez apporter à vos calculs lorsque vous n’avez qu’un seul degré de liberté. C’est ce qu’on appelle la « correction de continuité », ou parfois la correction de Yates. Souvenez-vous de ce j’ai souligné plus tôt : le test \(\chi^{2}\) est basé sur une approximation, en particulier sur l’hypothèse que la distribution binomiale commence à ressembler à une distribution normale lorsque N est grand. Le problème avec cela est qu’il ne fonctionne souvent pas bien, surtout quand vous avez seulement 1 degré de liberté (par exemple, lorsque vous faites un test d’indépendance sur une table de contingence 2 x 2). La raison principale est que la vraie distribution d’échantillonnage pour la statistique \(X^{2}\) est en fait discrète (parce qu’il s’agit de données catégorielles !) mais la distribution \(\chi^{2}\) est continue. Cela peut introduire des problèmes systématiques. Plus précisément, lorsque \(N\) est petit et que df = 1, la statistique de la qualité de l’ajustement tend à être « trop grande », ce qui signifie que vous avez en fait une valeur \(\alpha\) plus grande que vous ne le pensez (ou, de manière équivalente, les valeurs p sont un peu trop petites).

Yates (1934) a suggéré une solution simple, dans laquelle vous redéfinissez la statistique de la qualité de l’ajustement comme :

\[ \chi^{2} = \sum_{i}^{}\frac{\left( \mid E_{i} - O_{i} \mid - 0,5 \right)^{2}}{E_{i}} \]

En gros, il soustrait juste 0,5 partout.

D’après ce que j’en sais d’après l’article de Yates, la correction est essentiellement un bricolage. Elle ne découle d’aucune théorie fondée sur des principes. Elle repose plutôt sur un examen du comportement du test et sur l’observation que la version corrigée semble mieux fonctionner. Vous pouvez spécifier cette correction dans Jamovi à partir d’une case à cocher dans les options « Statistics », où elle est appelée « \(\chi^{2}\) continuity correction ».

10.4 Taille de l’effet

Comme nous l’avons mentionné précédemment (section 9.8), il est de plus en plus courant de demander aux chercheurs de déclarer une certaine mesure de la taille de l’effet. Supposons donc que vous ayez effectué votre test du chi carré, qui s’avère important. Vous savez donc maintenant qu’il y a une certaine association entre vos variables (test d’indépendance) ou un certain écart par rapport aux probabilités spécifiées (test d’ajustement). Vous voulez maintenant déclarer une mesure de l’ampleur de l’effet. Autrement dit, étant donné qu’il y a une association ou une déviation, quelle est sa force ?

Il existe différentes mesures que vous pouvez choisir de déclarer et plusieurs outils différents que vous pouvez utiliser pour les calculer. Je ne les aborderai pas tous, mais je me concentrerai plutôt sur les mesures de la taille de l’effet les plus couramment utilisés.

Par défaut, les deux mesures que les gens ont tendance à déclarer le plus souvent sont la statistique \(\phi\) et la version supérieure, connue sous le nom de V.

Mathématiquement, ils sont très simples. Pour calculer la statistique \(\phi\), il suffit de diviser votre valeur \(\chi^{2}\) par la taille de l’échantillon et de prendre la racine carrée :

\[ \phi = \sqrt{\frac{X^{2}}{N}} \]

L’idée ici est que la statistique de \(\phi\) est supposée se situer entre 0 (aucune association du tout) et 1 (association parfaite), mais elle ne le fait pas toujours quand votre tableau de contingence est plus grand que 2x2, ce qui est une vraie difficulté. Pour des tables plus grandes, il est en fait possible d’obtenir \(\phi< 1\), ce qui est plutôt insatisfaisant. Ainsi, pour corriger cela, les gens préfèrent généralement rapporter la statistique V proposée par Cramer (1999). C’est un ajustement assez simple à \(\phi\). Si vous avez un tableau de contingence avec r lignes et c colonnes, alors définissez \(k = min(r, c)\) comme étant la plus petite des deux valeurs. Si c’est le cas, la statistique V de Cramer est la suivante

\[ V = \sqrt{\frac{\chi^{2}}{N(k - 1)}} \]

Et c’est fini. Cela semble être une mesure assez populaire, probablement parce qu’elle est facile à calculer et qu’elle donne des réponses qui ne sont pas complètement idiotes. Avec le V de Crame, vous savez que la valeur varie vraiment de 0 (aucune association du tout) à 1 (association parfaite).

10.5 Hypothèses relatives au(x) test(s)

Tous les tests statistiques font des hypothèses, et c’est généralement une bonne idée de vérifier que ces hypothèses sont respectées. Pour les tests du chi carré dont il a été question jusqu’à présent dans ce chapitre, les hypothèses sont les suivantes :

• Les fréquences attendues sont suffisamment élevées. Rappelez-vous comment dans la section précédente nous avons vu que la distribution d’échantillonnage de \(\chi^{2}\) émerge parce que la distribution binomiale est assez similaire à une distribution normale ? Eh bien, comme nous l’avons vu au chapitre 7, cela n’est vrai que lorsque le nombre d’observations est suffisamment important. En pratique, cela signifie que toutes les fréquences attendues doivent être raisonnablement grandes. Quelle est la taille de raisonnablement grand ? Les opinions divergent, mais l’hypothèse par défaut semble être que vous aimeriez généralement voir toutes vos fréquences attendues supérieures à environ 5, bien que pour des tables plus grandes, vous seriez probablement d’accord si au moins 80% des fréquences attendues sont supérieures à 5 et aucune d’entre elles n’est inférieure à 1. Cependant, de ce que j’ai pu découvrir (par exemple,Cochran (1952)) cela semble avoir été proposé comme des lignes directrices générales, non des règles strictes, et elles semblent être assez prudentes (Larntz 1978).

• Les données sont indépendantes les unes des autres. Une hypothèse quelque peu cachée du test du chi carré est qu’il faut vraiment croire que les observations sont indépendantes. Précisons ce que je veux dire. Supposons que je m’intéresse à la proportion de bébés nés dans un hôpital donné qui sont des garçons. Je me promène dans les maternités et j’observe 20 filles et seulement 10 garçons. C’est une différence assez convaincante, non ? Mais plus tard, il s’est avéré que j’étais entré 10 fois dans la même salle et que je n’avais vu que 2 filles et 1 garçon. Ce n’est pas aussi convaincant, n’est-ce pas ? Mes 30 observations initiales étaient massivement non indépendantes, et n’équivalaient en fait qu’à 3 observations indépendantes. C’est évidemment un exemple extrême (et extrêmement stupide), mais il illustre la question fondamentale. La non-indépendance « empoisonne les données ». Parfois, cela vous pousse à rejeter faussement l’hypothèse nulle, comme l’illustre l’exemple stupide de l’hôpital, mais cela peut aussi aller dans l’autre sens. Pour donner un exemple un peu moins stupide, considérons ce qui se passerait si j’avais fait l’expérience des cartes un peu différemment au lieu de demander à 200 personnes d’essayer d’imaginer d’échantillonner une carte au hasard, supposons que je demande à 50 personnes de choisir 4 cartes. Une possibilité serait que chacun choisisse un coeur, un trèfle, un carreau et un pique (en accord avec l’heuristique de la représentativité ;Tversky & Kahneman (1973). C’est un comportement particulièrement non aléatoire de la part des gens, mais dans ce cas, j’obtiendrais une fréquence observée de 50 pour les quatre couleurs. Pour cet exemple, le fait que les observations ne soient pas indépendantes (parce que les quatre cartes que vous choisirez seront liées les unes aux autres) conduit en fait à l’effet inverse, conserver faussement l’hypothèse nulle.

Si vous vous trouvez dans une situation où l’indépendance est violée, il est possible d’utiliser le test de McNemar (dont nous parlerons) ou le test de Cochran (dont nous ne parlerons pas). De même, si le nombre de cellules attendu est trop faible, vérifiez le test exact de Fisher. C’est à ces sujets que nous nous intéressons maintenant.

10.6 Le test exact de Fisher

Que faire si votre nombre de cellules est trop faible, mais que vous souhaitez quand même tester l’hypothèse nulle que les deux variables sont indépendantes ? L’une des réponses serait de « recueillir plus de données », mais c’est beaucoup trop désinvolte. Il y a beaucoup de situations dans lesquelles il serait impossible ou contraire à l’éthique de le faire. Si c’est le cas, les statisticiens ont une sorte d’obligation morale de fournir aux scientifiques de meilleurs tests. En l’occurrence, Fisher (1922) a aimablement fourni la bonne réponse à la question. Pour illustrer l’idée de base, supposons que nous analysons les données d’une expérience sur le terrain portant sur l’état émotionnel de personnes qui ont été accusées de sorcellerie, dont certaines sont actuellement brûlées sur le bûcher.[Cet exemple est basé sur une plaisanterie publiée dans un article du Journal of Irreproducible Results.] Malheureusement pour le scientifique (mais heureusement pour la population en général), il est en fait très difficile de trouver des personnes en train d’être brûlées, de sorte que le nombre de d’observations est très faible dans certains cas. Un tableau de contingence des données salem.csv illustre ce point :

	Brûlée
Heureuse	FAUX	VRAI
FAUX	3	3
VRAI	10	0

En regardant ces données, il serait difficile de ne pas soupçonner que les gens qui ne sont pas brulés sont plus susceptibles d’être heureux que ceux qui sont brûlés. Cependant, le test du khi-carré le rend très difficile à tester en raison de la petite taille de l’échantillon. Donc, en tant que personne qui ne veut pas être brûlée, j’aimerais vraiment obtenir une meilleure réponse que celle-ci. C’est là que le test exact de Fisher (Fisher 1922) est très utile.

Le test exact de Fisher fonctionne un peu différemment du test du chi carré (ou en fait de tout autre test d’hypothèse dont je parle dans ce livre) dans la mesure où il n’a pas de statistique de test, mais il calcule « directement » la valeur p. J’expliquerai les bases du fonctionnement du test pour un tableau de contingence 2X2. Comme avant, voyons la notation:

	Heureuse	Triste	Total
Brûlée	O11	O12	R1
Non brûlée	O21	O22	R2
Total	C1	C1	N

Pour construire le test, Fisher traite les totaux des lignes et des colonnes (R₁, R₂, C₁ et C₂) comme des quantités fixes connues, puis calcule la probabilité que nous aurions obtenu les fréquences observées (O₁₁, O₁₂, O₂₁ et O₂₂) avec ces totaux. Dans la notation que nous avons développée au chapitre 7, ceci est écrit :

\[P(O_{11}, O_{12}, O_{21}, O_{22} \mid R_{1}, R_{2}, C_{1}, C_{2})\]

et comme vous pouvez l’imaginer, c’est un exercice un peu délicat de savoir quelle est cette probabilité. Mais il s’avère que cette probabilité est décrite par une distribution connue sous le nom de distribution hypergéométrique. Ce que nous devons faire pour calculer notre valeur p est de calculer la probabilité d’observer ce tableau particulier ou un tableau qui est « plus extrême »⁷⁸. Dans les années 1920, le calcul de cette somme était décourageant même dans les situations les plus simples, mais de nos jours, c’est assez facile tant que les tables ne sont pas trop grandes et que l’échantillon n’est pas trop grand. La question conceptuellement délicate est de savoir ce que cela signifie de dire qu’une table de contingence est plus « extrême » qu’une autre. La solution la plus simple est de dire que la table avec la probabilité la plus faible est la plus extrême. Ceci nous donne alors la valeur p.

Vous pouvez spécifier ce test dans Jamovi à partir d’une case à cocher dans les options « Statistics » de l’analyse « Contingency Tables ». Lorsque vous le faites avec les données du fichier salem.csv, la statistique exacte du test de Fisher est affichée dans les résultats. La principale chose qui nous intéresse ici est la valeur de p (p-value), qui dans ce cas est suffisamment petite (p<.036) pour justifier le rejet de l’hypothèse nulle que les personnes brûlées sont aussi heureuses que celles qui ne le sont pas. Voir la Figure 11‑6.

Figure 10‑6 :Sortie du test exact de Fisher dans Jamovi. Ignorez la « Valeur » et référez-vous simplement à la valeur p.

10.7 Le test McNemar

Supposons que vous ayez été embauché pour travailler pour le Parti politique générique australien (AGPP) et qu’une partie de votre travail consiste à déterminer l’efficacité des publicités politiques de l’AGPP. Vous décidez donc de constituer un échantillon de N = 100 personnes et de leur demander de regarder les publicités de l’AGPP. Avant qu’ils répondent, vous leur demandez s’il a l’intention de voter pour l’AGPP, puis après avoir montré les annonces, vous leur demandez à nouveau s’il a changé d’avis. Évidemment, si vous êtes bon dans votre travail, vous feriez aussi beaucoup d’autres choses, mais considérons juste cette simple expérience. Une façon de décrire vos données est d’utiliser le tableau de contingence suivant :

	Avant	Après	Total
Oui	30	10	40
Non	70	90	160
Total	100	100	200

Au premier abord, vous pourriez penser que cette situation se prête au test d’indépendance de Pearson \(\chi^{2}\) (voir la section 10.2). Cependant, un peu de réflexion révèle que nous avons un problème. Nous avons 100 participants mais 200 observations. C’est parce que chaque personne nous a fourni une réponse à la fois dans la colonne avant et dans la colonne après. Cela signifie que les 200 observations ne sont pas indépendantes les unes des autres. Si l’électeur A dit « oui » la première fois et que l’électeur B dit « non », on s’attendrait à ce que l’électeur A dise « oui » la deuxième fois plutôt que l’électeur B ! La conséquence en est que le test habituel de \(\chi^{2}\) ne donnera pas de réponses fiables en raison de la violation de l’hypothèse d’indépendance. Si c’était vraiment une situation rare, je ne perdrais pas mon temps à vous en parler. Mais ce n’est pas rare du tout. Il s’agit d’un plan standard à mesures répétées, et aucun des tests que nous avons considérés jusqu’à présent ne peut y faire face.

La solution au problème a été publiée par McNemar (1947). L’astuce consiste à commencer par organiser vos données d’une manière légèrement différente :

	Avant : Oui	Avant : Non	Total
Après : Oui	5	5	10
Après : Non	25	65	90
Total	30	70	100

Ce sont exactement les mêmes données, mais elles ont été réécrites de sorte que chacun de nos 100 participants apparaissent dans une seule cellule. Grâce à cette réécriture, l’hypothèse d’indépendance est maintenant satisfaite, et il s’agit d’un tableau de contingence que nous pouvons utiliser pour construire une statistique d’ajustement \(\chi^{2}\) Cependant, comme nous le verrons, nous devons le faire d’une manière légèrement non standard. Pour voir ce qui se passe, il est utile d’étiqueter les entrées de notre tableau un peu différemment :

	Avant : Oui	Avant : Non	Total
Après : Oui	a	b	a + b
Après : Non	c	d	c + d
Total	a + c	b + d	n

Pensons ensuite à notre hypothèse nulle : elle pose que le test « avant » et le test « après » ont la même proportion de personnes qui disent « Oui, je voterai pour AGPP ». En raison de la façon dont nous avons réécrit les données, cela signifie que nous vérifions maintenant l’hypothèse que les totaux des lignes et des colonnes proviennent de la même distribution. Ainsi, l’hypothèse nulle du test de McNemar est que nous avons une « homogénéité marginale ». En d’autres termes, les totaux de ligne et les totaux de colonne ont la même répartition : Pa + Pb = Pa + Pc, de même que Pc + Pd = Pb + Pd. Notez que cela signifie que l’hypothèse nulle se simplifie en fait à P_b=P_c. En d’autres termes, en ce qui concerne le test McNemar, seules les entrées hors diagonale de ce tableau (c.-à-d. b et c) comptent ! Après l’avoir remarqué, le test de McNemar de l’homogénéité marginale n’est pas différent d’un test \(\chi^{2}\) habituel. Après avoir appliqué la correction de Yates, notre statistique de test devient :

\[ \chi^{2} = \frac{\left( \mid b - c \mid - 0,5 \right)^{2}}{b + c} \]

ou, pour revenir à la notation que nous avons utilisée plus tôt dans ce chapitre :

\[ \chi^{2} = \frac{\left( \mid O_{12} - O_{21} \mid - 0,5 \right)^{2}}{O_{12} + O_{21}} \]

et cette statistique a une distribution \(\chi^{2}\) (approximativement) avec df = 1. Cependant, rappelez-vous que, comme les autres tests \(\chi^{2}\), il ne s’agit que d’une approximation, vous devez donc avoir un nombre de d’observations raisonnablement élevé pour que cela fonctionne.

10.7.1 Faire le test McNemar dans Jamovi

Maintenant que vous savez ce qu’est le test McNemar, faisons-en un. Le fichier agpp.csv contient les données brutes dont j’ai parlé précédemment. L’ensemble de données de l’agpp contient trois variables, une variable id qui identifie chaque participant dans l’ensemble de données (nous verrons pourquoi c’est utile dans un instant), une variable response_before qui enregistre la réponse de la personne quand on lui a posé la question la première fois, et une variable response_after qui montre la réponse qu’elle a donnée quand on a posé la même question une deuxième fois. Notez que chaque participant n’apparaît qu’une seule fois dans cet ensemble de données. Allez dans l’analyse « Analyses » - « Frequencies » - « Contingency Tables » -Paired Samples’ dans Jamovi, et déplacez response_before dans la case « Rows », et response_after dans la case « Column ». Vous obtiendrez alors un tableau de contingence dans la fenêtre des résultats, avec la statistique pour le test McNemar juste en dessous, voir Figure 10‑7.

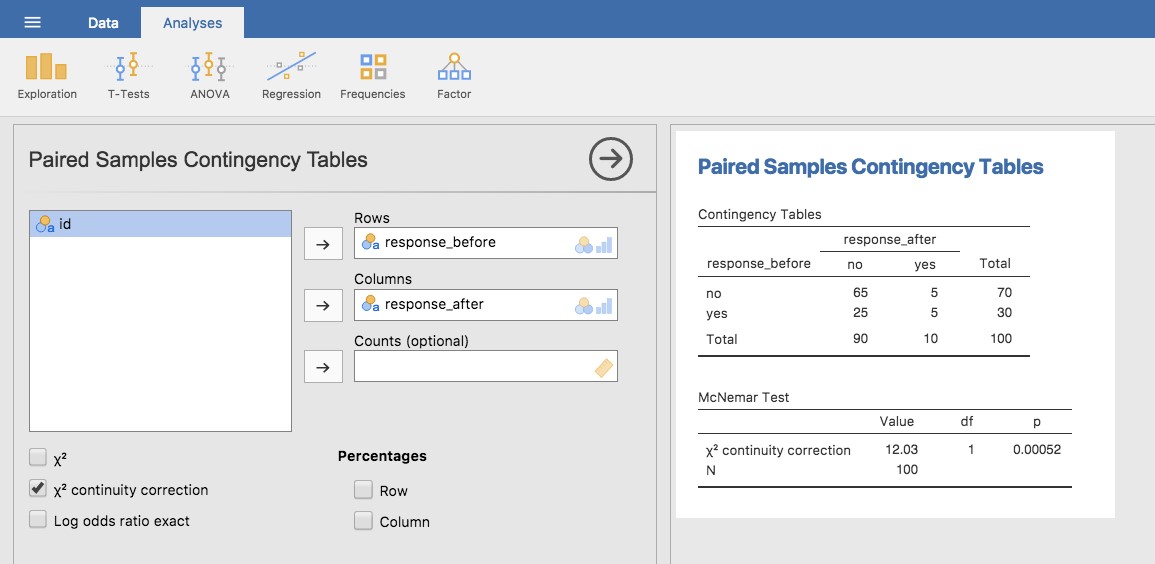
Figure 10‑7 : McNemar test de sortie dans Jamovi

Et c’est fini ! Nous venons de faire un test de McNemar pour déterminer si les gens étaient tout aussi susceptibles de voter pour l’AGPP après les annonces qu’ils ne l’étaient avant. Le test était significatif (\(\chi^{2}(1) = 12,03, p< .001\)), suggérant qu’ils ne l’étaient pas. Et, en fait, il semble que les publicités aient eu un effet négatif : les gens étaient moins enclins à voter pour AGPP après avoir vu les publicités. Ce qui est tout à fait logique si l’on considère la qualité d’une publicité politique typique.

10.8 Quelle est la différence entre McNemar et l’indépendance ?

Revenons au début du chapitre et regardons à nouveau l’ensemble des données des cartes. Si vous vous souvenez bien, le plan expérimental que j’ai décrit impliquait que les gens faisaient deux choix. Comme nous disposons d’informations sur le premier et le second choix que chacun a fait, nous pouvons construire le tableau de contingence suivant qui croise le premier choix et le second choix.

	choix_2
choix_1	Trèfles	Carreaux	Cœurs	Piques
Trèfles	10	9	10	6
Carreaux	20	4	13	14
Coeur	20	18	3	23
Piques	18	13	15	4

Supposons que je voulais savoir si le choix que vous faites la deuxième fois dépend du choix que vous avez fait la première fois. C’est là qu’un test d’indépendance est utile, et ce que nous essayons de faire est de voir s’il y a une relation entre les lignes et les colonnes de ce tableau.

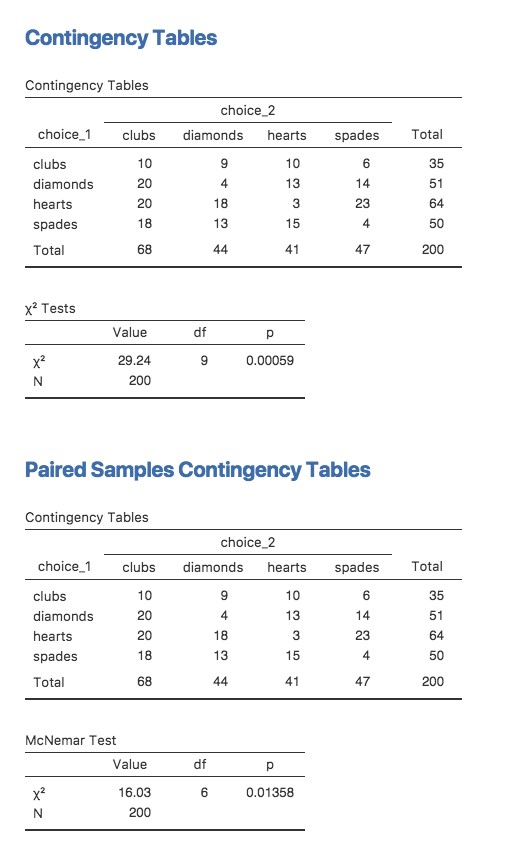
Figure 10‑8 : Sortie d’un test d’indépendance ou apparié (McNemar) dans Jamovi

Sinon, supposons que je veuille savoir si, en moyenne, les fréquences des choix de cartes sont différentes la deuxième fois que la première fois. Dans cette situation, ce que j’essaie vraiment de voir, c’est si les totaux des lignes sont différents des totaux des colonnes. Pour cela, vous utilisez le test McNemar.

Les différentes statistiques produites par ces différentes analyses sont présentées à la Figure 10‑8. Notez que les résultats sont différents ! Ce n’est pas le même test.

10.9 Résumé

Les idées clés discutées dans ce chapitre sont :

• Le test d’adéquation \(\chi^{2}\) (chi carré) (section 10.1) est utilisé lorsque vous avez un tableau des fréquences observées de différentes catégories, et l’hypothèse nulle vous donne un ensemble de probabilités « connues » pour les comparer.

• Le test d’indépendance \(\chi^{2}\) (chi carré) (section 10.2) est utilisé lorsque vous disposez d’un tableau de contingence (tableau croisé) de deux variables catégorielles. L’hypothèse nulle est qu’il n’y a aucune relation ou association entre les variables.

• La taille de l’effet d’un tableau de contingence peut être mesurée de plusieurs façons (section 10.4). En particulier, nous avons vu la statistique V de Cramer.

• Les deux versions du test de Pearson reposent sur deux hypothèses : que les fréquences attendues sont suffisamment élevées et que les observations sont indépendantes (section 10.5). Le test exact de Fisher (section 10.6) peut être utilisé lorsque les fréquences attendues sont faibles. Le test de McNemar (section 10.7) peut être utilisé pour certains types de violations de l’indépendance.

Si vous souhaitez en savoir plus sur l’analyse des données catégorielles, Agresti (1996), qui, comme son titre l’indique, fournit une introduction à l’analyse des données catégorielles, est un bon premier choix. Si le livre d’introduction ne vous suffit pas (ou ne peut pas résoudre le problème sur lequel vous travaillez), vous pouvez consulter Agresti (2013), Categorical Data Analysis. Ce dernier est un texte plus avancé, il n’est donc probablement pas sage de sauter directement de ce livre à celui-là.

References

Agresti, Alan. 1996. An Introduction to Categorical Data Analysis. New York: John Wiley & Sons.

Agresti, Alan. 2013. Categorical Data Analysis. Third. Wiley.

Cochran, William G. 1952. “The \(X\)2 Test of Goodness of Fit.” The Annals of Mathematical Statistics 23 (3): 315–45.

Cramer, Harald. 1999. Mathematical Methods of Statistics. 19. printing. Princeton Landmarks in Mathematics and Physics. Princeton: Princeton Univ. Press.

Fisher, R. A. 1922. “On the Interpretation of \(X\)2 from Contingency Tables, and the Calculation of P.” Journal of the Royal Statistical Society 85 (1): 87–94. https://doi.org/10.2307/2340521.

Kahneman, Daniel, and Amos Tversky. 1973. “On the Psychology of Prediction.” Psychological Review 80 (4): 237–51. https://doi.org/10.1037/h0034747.

Larntz, Kinley. 1978. “Small-Sample Comparisons of Exact Levels for Chi-Squared Goodness-of-Fit Statistics.” Journal of the American Statistical Association 73 (362): 253–63. https://doi.org/10.2307/2286650.

McNEMAR, Q. 1947. “Note on the Sampling Error of the Difference Between Correlated Proportions or Percentages.” Psychometrika 12 (2): 153–57. https://doi.org/10.1007/bf02295996.

Pearson, Karl. 1900. “X. On the Criterion That a Given System of Deviations from the Probable in the Case of a Correlated System of Variables Is Such That It Can Be Reasonably Supposed to Have Arisen from Random Sampling.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 50 (302): 157–75. https://doi.org/10.1080/14786440009463897.

Yates, F. 1934. “Contingency Tables Involving Small Numbers and the \(X\)2 Test.” Supplement to the Journal of the Royal Statistical Society 1 (2): 217–35. https://doi.org/10.2307/2983604.

---

66. Parfois aussi appelé “chi-carré”.↩︎

67. Un vecteur est une séquence d’éléments de données du même type basique↩︎

68. Si vous réécrivez l’équation pour la statistique d’ajustement comme une somme sur k -1 valeurs indépendantes, vous obtenez la distribution d’échantillonnage « correcte », qui est le chi carré avec k - 1 degrés de liberté. C’est au-delà de la portée d’un livre d’introduction que de montrer les développements mathématiques avec autant de détails. Tout ce que je voulais faire, c’est vous donner une idée de la raison pour laquelle la statistique d’ajustement est associée à la distribution du chi carré.↩︎

69. Je me sens obligé de souligner qu’il s’agit d’une simplification excessive. Cela fonctionne très bien dans de nombreuses situations, mais de temps en temps, nous rencontrons des valeurs de degrés de liberté qui ne sont pas des nombres entiers. Ne vous inquiétez pas trop ; quand vous rencontrez cela, rappelez-vous simplement que “degrés de liberté” est en fait un concept un peu foullis, et que la belle présentation simple que je vous fais ici n’est pas la présentation entière. Pour un cours d’introduction, il est généralement préférable de s’en tenir à la présentation simple, mais je pense qu’il est préférable de vous avertir que cette présentation simple va s’effondrer. Si je ne vous avais pas donné cet avertissement, vous pourriez commencer à vous tromper en voyant df = 3,4 ou quelque chose comme ça, pensant (à tort) que vous aviez mal compris ce que je vous ai appris plutôt que de réaliser (correctement) qu’il y a quelque chose que je ne vous ai jamais dit.↩︎

70. Dans la pratique, la taille de l’échantillon n’est pas toujours fixe. Par exemple, nous pourrions mener l’expérience sur une période de temps fixe et le nombre de participants dépend du nombre de personnes qui se présentent. Cela n’a pas d’importance pour les objectifs actuels.↩︎

71. NdT : l’abréviation française de degré de liberté est ddl, mais nous conservons l’abréviation anglaise df (degree of freedom) qui est utilisée dans les sorties Jamovi.↩︎

72. Les conventions relatives à la façon dont les statistiques doivent être présentées ont tendance à différer quelque peu d’une discipline à l’autre. J’ai tendance à m’en tenir à la façon dont les choses se font en psychologie, puisque c’est ce que je fais. Mais le principe général de fournir suffisamment d’informations au lecteur pour lui permettre de vérifier vos résultats est assez universel, je pense.↩︎

73. Pour certains, ce conseil peut sembler étrange, ou du moins en contradiction avec les conseils « habituels » sur la façon de rédiger un rapport technique. En règle générale, on dit aux élèves que la section « résultats » d’un rapport sert à décrire les données et à présenter une analyse statistique, tandis que la section « discussion » sert à fournir une interprétation. C’est vrai jusqu’à un certain point, mais je pense que les gens l’interprètent souvent beaucoup trop littéralement. La façon dont je l’aborde habituellement est de fournir une interprétation rapide et simple des données dans la section des résultats, afin que mon lecteur comprenne ce que les données nous disent. Puis, au cours de la discussion, j’essaie de tenir un discours plus générale sur la façon dont mes résultats s’intègrent au reste de la littérature scientifique. Bref, ne laissez pas le conseil « l’interprétation va dans la discussion » transformer votre section de résultats en un fouillis incompréhensible. Il est beaucoup plus important d’être compris par votre lecteur.↩︎

74. Pour compliquer les choses, le test d’ajustement est un cas particulier de toute une classe de tests connus sous le nom de tests du rapport de vraisemblance (Likehood ratio test ; LRT). Je ne traite pas des LRT dans ce livre, mais ce sont des choses très pratiques à savoir.↩︎

75. Note technique. La façon dont j’ai décrit le test prétend que les totaux des colonnes sont fixes (c.-à-d. que le chercheur avait l’intention de sonder 87 robots et 93 humains) et que les totaux des rangées sont aléatoires (c.-à-d. qu’il s’avère que 28 personnes ont choisi le chiot). Pour reprendre la terminologie de mon manuel de statistiques mathématiques (Hogg and Craig 2005), je devrais techniquement qualifier cette situation de test du Khi-deux d’homogénéité et réserver le terme test du Khi-carré d’indépendance à la situation où les totaux des lignes et des colonnes sont des résultats aléatoires de l’expérience. Dans les premières ébauches de ce livre, c’est exactement ce que j’ai fait. Cependant, il s’avère que ces deux tests sont identiques, et je les ai donc regroupés.↩︎

76. Techniquement, E_ij ici est une estimation, donc je devrais probablement l’écrire \(\hat{E}_{ij}\). Mais comme personne d’autre ne le fait, moi non plus.↩︎

77. Un problème dont beaucoup d’entre nous s’inquiètent dans la vraie vie.↩︎

78. Il n’est pas surprenant que le test exact de Fisher soit motivé par l’interprétation de Fisher d’une valeur p, et non par celle de Neyman ! Voir la section 9.5.↩︎