Chapitre 14 ANOVA Factorielle

Au cours des derniers chapitres, nous avons fait pas mal de choses. Nous avons examiné les tests statistiques que vous pouvez utiliser lorsque vous avez une variable prédictive nominale à deux groupes (c.-à-d. le test t, chapitre 11) ou à trois groupes ou plus (p. ex. ANOVA à un facteur, chapitre 13). Le chapitre sur la régression (chapitre 12) a introduit une nouvelle idée puissante, à savoir la construction de modèles statistiques avec de multiples variables prédicteurs continues utilisées pour expliquer une seule variable résultat. Par exemple, un modèle de régression pourrait être utilisé pour prédire le nombre d’erreurs qu’un élève commet dans un test de compréhension de la lecture en fonction du nombre d’heures qu’il a étudiées pour le test et de son résultat à un test de QI normalisé.

Le but de ce chapitre est d’étendre l’idée d’utiliser plusieurs variables prédictrices dans le cadre de l’analyse de variance. Supposons, par exemple, que nous voulions utiliser le test de compréhension de la lecture pour mesurer le rendement des élèves dans trois écoles différentes, et que nous soupçonnons que les filles et les garçons se développent à des rythmes différents (et que l’on s’attendrait donc à ce qu’ils aient en moyenne des performances différentes). Chaque élève est classé de deux façons différentes : en fonction de son sexe et en fonction de son école. Ce que nous aimerions faire, c’est d’analyser les résultats de compréhension de la lecture en fonction de ces deux variables de regroupement. L’outil pour ce faire est appelé ANOVA factorielle. Toutefois, comme nous avons deux variables de regroupement, nous l’appelons parfois analyse de variance bifactorielle, contrairement aux analyses de variance à un facteur que nous avons effectuées au chapitre 13.

14.1 ANOVA Factorielle 1 : des plans équilibrés, pas d’interactions

Lorsque nous avons discuté de l’analyse de la variance au chapitre 13, nous avons supposé un plan expérimental assez simple. Chaque personne fait partie d’un groupe parmi d’autres et nous voulons savoir si ces groupes ont des scores moyens différents pour une variable résultats. Dans la présente section, je traiterai d’une catégorie plus large de plans expérimentaux appelés plans factoriels, dans lesquels nous avons plus d’une variable de groupement. J’ai donné ci-dessus un exemple de la façon dont ce genre de plan pourrait être réalisé. Nous avons vu un autre cas de figure au chapitre 13, dans lequel nous examinions l’effet de différents médicaments sur le l’amélioration de l’humeur ressenti par chaque personne. Dans ce chapitre, nous avons trouvé un effet important du médicament, mais à la fin du chapitre, nous avons également effectué une analyse pour voir s’il y avait un effet de la thérapie. Nous n’en avons pas trouvé, mais il y a quelque chose d’un peu inquiétant à essayer d’effectuer deux analyses distinctes pour prédire la même variable résultat. Peut-être qu’il y a un effet de la thérapie sur le gain d’humeur, mais nous n’avons pas pu le trouver parce qu’il était « caché » par l’effet du médicament? En d’autres termes, nous voulons effectuer une analyse unique qui inclut à la fois le médicament et la thérapie comme prédicteurs. Pour cette analyse, chaque personne est classée selon le médicament qu’on lui a administré (un facteur à 3 niveaux) et la thérapie qu’elle a reçue (un facteur à 2 niveaux). C’est ce que nous appelons un plan factoriel 3 x 2.

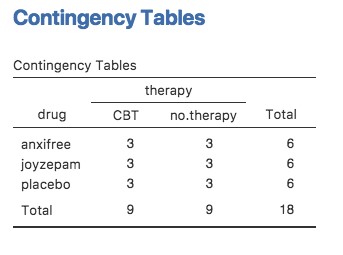
Si l’on croise les données sur les médicaments par traitement, en utilisant l’analyse « Frequencies » - « Contingency Tables » de Jamovi (voir la section 6.1), on obtient le tableau présenté à la Figure 14‑1.

Figure 14‑1 : Tableau de contingence Jamovi du drug par therapy

Comme vous pouvez le constater, non seulement nous avons des participants correspondant à toutes les combinaisons possibles des deux facteurs, ce qui indique que notre plan est complètement croisé¹²¹, mais il s’avère qu’il y a un nombre égal de personnes dans chaque groupe. En d’autres termes, nous avons un plan équilibré. Dans cette section, je parlerai de la façon d’analyser les données à partir de plans équilibrés, puisque c’est le cas le plus simple. L’histoire des plans déséquilibrées est assez fastidieuse, nous allons donc la mettre de côté pour l’instant.

14.1.1 Quelles hypothèses vérifions-nous ?

Comme l’analyse de variance à un facteur, l’analyse de variance factorielle est un outil permettant de tester certains types d’hypothèses sur les moyennes de population. Un bon point de départ serait donc d’être explicite sur ce que sont réellement nos hypothèses. Cependant, avant même d’en arriver là, il est vraiment utile d’avoir une notation claire et simple pour décrire les moyennes de la population. Étant donné que les observations sont classées selon deux facteurs différents, il existe un grand nombre de moyennes auxquels on peut s’intéresser. Pour voir cela, commençons par penser à tous les échantillons que l’on peut calculer pour ce type de plan. Tout d’abord, il y a l’idée évidente que nous pourrions nous intéresser à cette liste de moyennes de groupe :

Ce tableau présente une liste des moyennes de groupe pour toutes les combinaisons possibles des deux facteurs (p. ex. les personnes qui ont reçu le placebo et aucune thérapie, les personnes qui ont reçu le placebo en recevant la TCC (=CBT), etc.) Il est utile d’organiser tous ces chiffres, ainsi que les moyennes marginales et générales, dans un tableau unique qui ressemble à celui-ci :

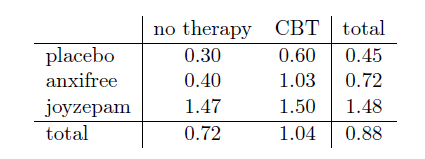
Chacune de ces moyennes correspond bien sûr à un échantillon de statistiques. C’est une quantité qui se rapporte aux observations précises que nous avons faites dans notre étude. Ce que nous voulons déduire, ce sont les paramètres correspondants de la population. C’est-à-dire, les vraies moyennes telles qu’elles existent au sein d’une population plus large. Ces moyennes de population peuvent aussi être organisées dans un tableau similaire, mais nous aurons besoin d’une petite notation mathématique pour le faire. Comme d’habitude, j’utiliserai le symbole µ pour désigner une moyenne de population. Cependant, parce qu’il y a beaucoup de moyennes différentes, j’utiliserai des indices pour les distinguer.

Voici comment fonctionne la notation. Notre tableau est défini en fonction de deux facteurs. Chaque ligne correspond à un niveau différent de facteur A (dans ce cas-ci, drug) et chaque colonne correspond à un niveau différent de facteur B (dans ce cas, therapy). Si nous indiquons par R, le nombre de lignes dans le tableau, et C, le nombre de colonnes, nous pouvons nous référer à cela comme une ANOVA factorielle RxC. Dans ce cas, R = 3 et C = 2. Nous utiliserons des lettres minuscules pour faire référence à des lignes et colonnes spécifiques, de sorte que µrc se réfère à la moyenne de population associée au r-ième niveau du facteur A (c’est-à-dire le numéro de ligne r) et au c-ième niveau du facteur B (numéro de colonne c).¹²² Ainsi, les moyennes de la population sont maintenant écrites comme ceci :

Bien, qu’en est-il des cases restantes ? Par exemple, comment décrire le gain d’humeur moyen dans l’ensemble de la population (hypothétique) qui pourraient recevoir du Joyzepam dans le cadre d’une expérience comme celle-ci, qu’elles aient été ou non en thérapie ? Nous utilisons la notation « point » pour l’exprimer. Dans le cas de Joyzepam, notez qu’il s’agit de la moyenne associée à la troisième ligne du tableau. C’est-à-dire que nous calculons la moyenne sur deux moyennes cellules (c.-à-d. µ31 et µ32). Le résultat de ce calcul de la moyenne est appelé moyenne marginale et, dans ce cas, il s’agit de µ3.. La moyenne marginale de la TCC correspond à la moyenne de la population associée à la deuxième colonne du tableau ; nous utilisons donc la notation µ.2 pour la désigner. La moyenne générale est désignée par µ.. parce qu’il s’agit de la moyenne obtenue en moyennant (en marginalisant¹²³) sur les deux. Ainsi, notre tableau complet des moyennes de population peut être écrit de la façon suivante :

Maintenant que nous avons cette notation, il est facile de formuler et d’exprimer certaines hypothèses. Supposons que le but est de découvrir deux choses. Premièrement, le choix du médicament a-t-il un effet sur l’humeur ? Deuxièmement, la TCC a-t-elle un effet sur l’humeur ? Ce ne sont pas les seules hypothèses que nous pourrions formuler, bien sûr, et nous verrons un exemple très important d’un autre type d’hypothèse à la section 14.2, mais ce sont les deux hypothèses les plus simples à vérifier, et nous allons donc commencer par là. Considérez le premier test. Si le médicament n’a pas d’effet, on s’attendrait à ce que tous les moyennes de la rangée soient identiques, n’est-ce pas ? Voilà donc notre hypothèse nulle. D’un autre côté, si le médicament a de l’importance, il faut s’attendre à ce que les moyens de cette rangée soient différents. Formellement, nous écrivons nos hypothèses nulles et alternatives en termes d’égalité des moyennes marginales :

Hypothèse nulle, H₀: Les moyennes en ligne sont les mêmes, c.-à-d. \(\mu_{1}=\mu_{2}=\mu_{3}\) Hypothèse alternative, H₁ : La moyenne d’au moins une ligne est différente.

Il convient de noter qu’il s’agit exactement des mêmes hypothèses statistiques que celles que nous avons formulées lorsque nous avons effectué une analyse de variance à un facteur sur ces données au chapitre 13. A l’époque, j’utilisais la notation \(\mu_P\) pour faire référence au gain d’humeur moyen pour le groupe placebo, \(\mu_{A}\) et \(\mu_{J}\) correspondant à la moyenne du groupe pour les deux médicaments, et l’hypothèse nulle était \(\mu_{P} =\mu_{A} =\mu_{J}\). Nous parlons donc en fait de la même hypothèse, c’est juste que l’analyse de variance plus compliquée exige une notation plus prudente en raison de la présence de multiples variables de groupement, c’est pourquoi nous parlons maintenant de cette hypothèse comme de\(\mu_{.1}=\mu_{.2}=\mu_{.3}\). Cependant, comme nous le verrons plus loin, bien que l’hypothèse soit identique, le test de cette hypothèse est subtilement différent du fait que nous reconnaissons maintenant l’existence de la deuxième variable de groupement.

En parlant de l’autre variable de groupement, vous ne serez pas surpris de découvrir que notre deuxième test d’hypothèse est formulé de la même façon. Cependant, puisqu’il s’agit de la thérapie psychologique plutôt que du médicament, notre hypothèse nulle correspond maintenant à l’égalité des moyennes en colonne :

Hypothèse nulle, H₀: Les moyennes en colonne sont les mêmes, c.-à-d. \(\mu_{.1}=\mu_{.2}\)
Hypothèse alternative, H₁: Les moyennes des colonnes sont différentes, c-à-d. \(\mu_{.1}\neq\mu_{.2}\)

14.1.2 Réalisation de l’analyse dans Jamovi

Les hypothèses nulles et alternatives que j’ai décrites dans la dernière section devraient vous sembler terriblement familières. Il s’agit essentiellement des mêmes hypothèses que celles que nous avons testées dans nos analyses de variance à un facteur plus simples au chapitre 13. Vous vous attendez donc probablement à ce que les tests d’hypothèse utilisés dans l’analyse de variance factorielle soient essentiellement les mêmes que le test F du chapitre 13. Vous vous attendez à voir des références à des sommes de carrés (SS), des carrés moyens (MS), des degrés de liberté (df), et finalement une statistique F que nous pouvons convertir en une valeur p, n’est-ce pas ? Eh bien, vous avez tout à fait raison. A tel point que je vais m’écarter de mon approche habituelle. Tout au long de ce livre, j’ai généralement pris l’approche de décrire la logique (et dans une certaine mesure les aspects mathématiques) qui sous-tend une analyse particulière d’abord et seulement ensuite introduire l’analyse dans Jamovi. Cette fois, je vais le faire dans l’autre sens et vous montrer comment le faire en Jamovi d’abord. La raison en est que je veux souligner les similitudes entre le simple outil ANOVA à un facteur dont nous avons parlé au chapitre 13, et l’approche plus complexe que nous allons utiliser dans ce chapitre.

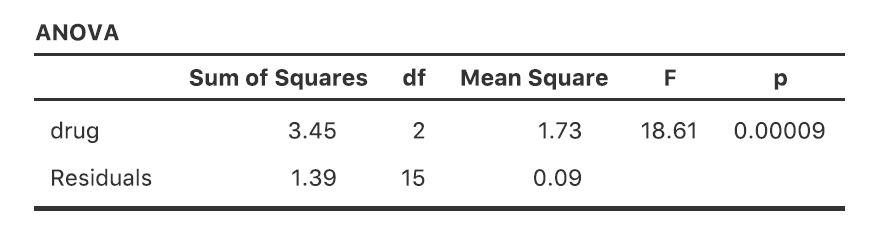
Si les données que vous essayez d’analyser correspondent à un plan factoriel équilibré, l’analyse de la variance est facile. Pour voir à quel point c’est facile, commençons par reproduire l’analyse originale du chapitre 13.Au cas où vous l’auriez oublié, pour cette analyse, nous n’utilisions qu’un seul facteur (c.-à-d. drug) pour prédire notre variable de résultat (c.-à-d. mood.gain), et nous avons obtenu les résultats présentés à la Figure 14‑2.

Figure 14‑2 : ANOVA à un facteur de mood.gain par drug avec Jamovi

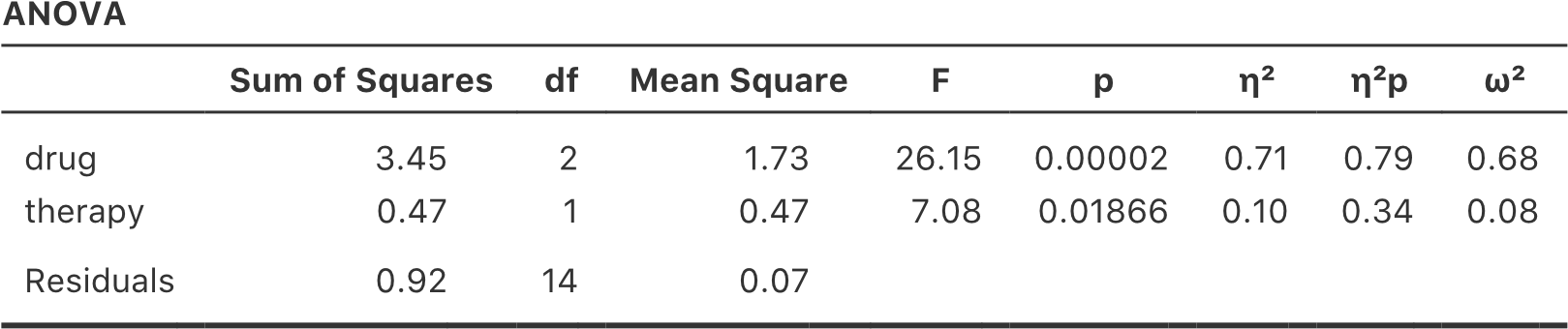
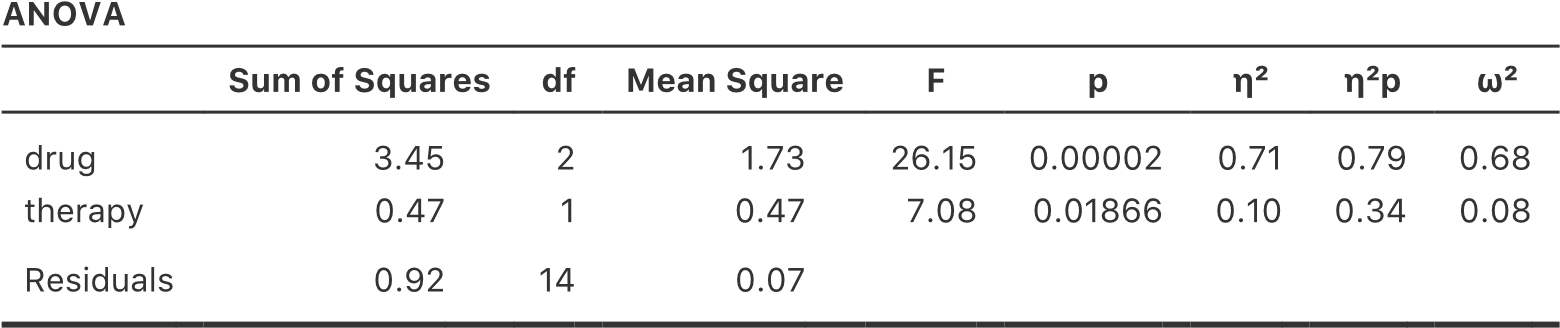
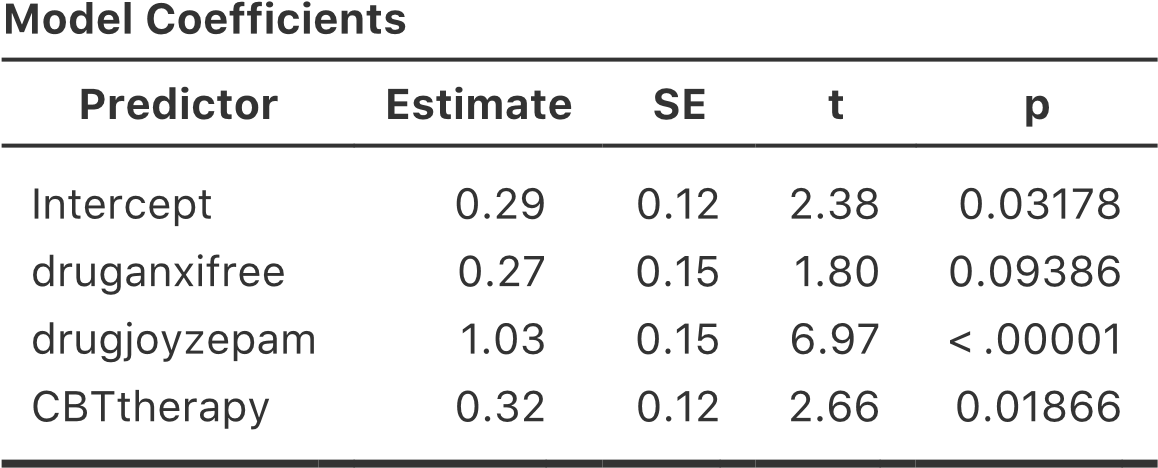
Maintenant, supposons que je sois aussi curieux de savoir si la therapy a une relation avec le mood.gain. A la lumière de ce que nous avons vu dans notre discussion sur la régression multiple au chapitre 12, vous ne serez probablement pas surpris qu’il nous suffise d’ajouter la therapy comme deuxième « Fixed Factor » dans l’analyse, voir la Figure 14‑3.

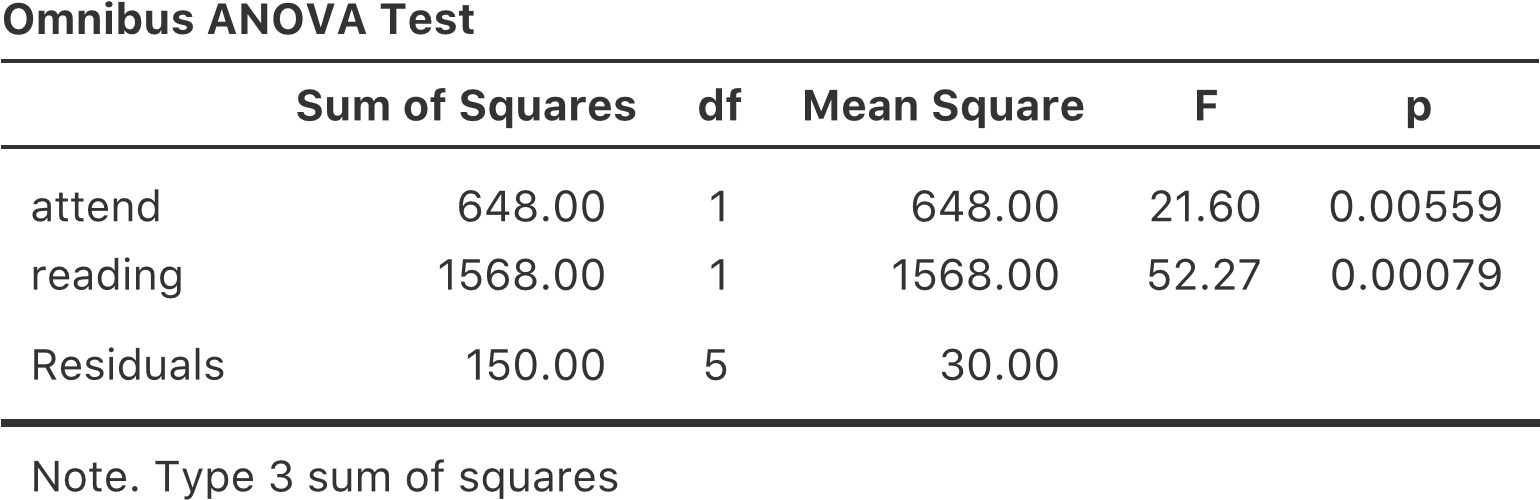
Cette sortie est assez simple à lire aussi. La première ligne du tableau indique la somme des carrés (SS) entre les groupes associés au facteur drug, ainsi que la valeur correspondante aux df inter groupes. Il calcule également un carré moyen (MS), une statistique F et une valeur p.

Figure 14‑3 Anova à deux facteurs dans Jamovi pour mood.gain par drug et therapy

Nous avons également une ligne correspondant au facteur therapy et une ligne correspondant aux résidus (c.-à-d. la variation intragroupe).

Non seulement toutes les quantités individuelles sont assez familières, mais les relations entre ces différentes quantités sont restées inchangées, tout comme nous l’avons vu avec l’ANOVA à un facteur. Notez que le carré moyen est calculée en divisant SS par le df correspondant. C’est-à-dire qu’il est toujours vrai que qu’il s’agisse de drug, de therapy ou des résidus.

\[ MS = \frac{\text{SS}}{\text{df}} \]

Pour le voir, ne nous inquiétons pas de la façon dont les sommes des carrés sont calculées. Au lieu de cela, prenons pour acquis que Jamovi a calculé correctement les valeurs SS, et essayons de vérifier que tous les autres nombres ont un sens. Tout d’abord, notons que pour le facteur drug, si on divise 3,45 par 2 et on obtient un carré moyen de 1,73. Pour le facteur therapy, il n’y a qu’un seul degré de liberté, donc nos calculs sont encore plus simples : diviser 0,47 (la valeur SS) par 1 nous donne un résultat de 0,47 (la valeur de MS).

En ce qui concerne les statistiques F et les valeurs p, notons que nous en avons deux de chaque, l’une correspondant au facteur drug et l’autre au facteur therapy. Peu importe de laquelle il s’agit, la statistique F est calculée en divisant le carrée moyen associé au facteur par le valeur carré moyen associé aux résidus. Si nous utilisons « A » comme notation abrégée pour désigner le premier facteur (facteur A ; dans ce cas, drug) et « R » comme notation abrégée pour désigner les résidus, alors la statistique F associée au facteur A est appelée F_A, et est calculée comme suit :

\[ F_{A} = \frac{\text{MS}_{A}}{\text{MS}_{R}} \]

et une formule équivalente existe pour le facteur B (c.-à-d. therapy). Notez que cette utilisation de « R » pour parler des résidus est un peu gênante, puisque nous avons également utilisé la lettre R pour faire référence au nombre de lignes dans le tableau, mais j’utiliserai « R » seulement pour désigner les résidus dans le contexte de SSR et MSR, donc j’espère que cela ne sera pas trop confus. Quoi qu’il en soit, pour appliquer cette formule au facteur drug, on prend le carré moyen de 1,73 et on le divise par le carré moyen résiduel de 0,07, ce qui nous donne une statistique F de 26,15. Le calcul correspondant pour la variable therapy serait de diviser 0,47 par 0,07, ce qui donne 7,08 pour la statistique F. Il n’est pas surprenant, bien sûr, que ces valeurs soient les mêmes que celles que Jamovi a rapportées dans le tableau ANOVA ci-dessus.

Le tableau ANOVA contient également le calcul des valeurs p. Encore une fois, il n’y a rien de nouveau ici. Pour chacun de nos deux facteurs, nous essayons de tester l’hypothèse nulle qu’il n’y a pas de relation entre le facteur et la variable résultat (je serai un peu plus précis à ce sujet plus loin). Pour ce faire, nous avons (apparemment) suivi une stratégie similaire à ce que nous avons fait dans le cadre d’ANOVA et nous avons calculé une statistique F pour chacune de ces hypothèses. Pour convertir ces valeurs en p, il suffit de noter que la distribution d’échantillonnage pour la statistique F sous l’hypothèse nulle (que le facteur en question n’est pas pertinent) est une distribution F. Notez également que les deux degrés de liberté sont ceux correspondant au facteur et aux résidus. Pour le facteur drug, il s’agit d’une distribution F avec 2 et 14 degrés de liberté (je reviendrai sur les degrés de liberté plus en détail plus loin). En revanche, pour le facteur therapy, la distribution d’échantillonnage est F avec 1 et 14 degrés de liberté.

À ce stade, j’espère que vous pouvez voir que le tableau ANOVA pour cette analyse factorielle plus complexe devrait être lu de la même façon que le tableau ANOVA pour l’analyse à un facteur plus simple. Bref, il nous dit que l’analyse de variance factorielle pour notre plan 3x2 a permis de trouver un effet significatif du médicament (F(2,14) = 26,15, p< .001) ainsi qu’un effet significatif du traitement (F(1,14) = 7,08, p =.02). Ou, pour utiliser la terminologie techniquement plus correcte, nous dirions qu’il y a deux effets principaux du médicament et de la thérapie. Pour l’instant, il semble probablement un peu redondant de parler d’effets « principaux », mais cela a du sens. Plus tard, nous parlerons de la possibilité « d’interactions » entre les deux facteurs, et nous ferons donc généralement une distinction entre les effets principaux et les effets d’interaction.

14.1.3 Comment la somme des carrés est-elle calculée ?

Dans la section précédente, j’avais deux objectifs. Tout d’abord, pour vous montrer que la méthode Jamovi nécessaire pour faire l’ANOVA factorielle est à peu près la même que celle que nous avons utilisée pour une ANOVA à un facteur. La seule différence est l’ajout d’un deuxième facteur. Deuxièmement, je voulais vous montrer à quoi ressemble le tableau ANOVA dans ce cas, afin que vous puissiez voir d’emblée que la logique et la structure de base de l’ANOVA factorielle sont les mêmes que celles qui sous-tendent l’ANOVA à un facteur. Essayez de vous accrocher à cette idée. C’est tout à fait vrai, dans la mesure où l’ANOVA factorielle est construite plus ou moins de la même manière que le modèle ANOVA à un facteur plus simple. C’est juste que ce sentiment de familiarité commence à s’évaporer une fois que vous commencez à creuser les détails. Traditionnellement, cette sensation réconfortante est remplacée par un besoin irrépressible de maltraiter les auteurs des manuels de statistiques.

Bien, commençons par examiner certains de ces détails. L’explication que j’ai donnée dans la dernière section illustre le fait que les tests d’hypothèse pour les principaux effets (du médicament et de la thérapie dans ce cas) sont des tests F, mais ce qu’il ne fait pas, c’est vous montrer comment la somme des valeurs des carrés (SS) est calculée. Il ne vous dit pas non plus explicitement comment calculer les degrés de liberté (valeurs df) bien que ce soit une chose simple en comparaison. Supposons pour l’instant que nous n’ayons que deux variables prédictrices, le facteur A et le facteur B. Si nous utilisons Y pour nous désigner la variable de résultat, nous utiliserions Y_rci pour nous parler du résultat associé au i-ième membre du groupe rc (c.-à-d. niveau/ligne r pour le facteur A et niveau/colonne c pour le facteur B). Ainsi, si l’on utilise \(\bar{Y}\) pour se référer à une moyenne d’échantillon, on peut utiliser la même notation que précédemment pour se référer aux moyennes de groupe, aux moyennes marginales et aux grandes moyennes. C’est-à-dire que \({\bar{Y}}_{rc}\) est la moyenne de l’échantillon associée au r-ième niveau du facteur A et le c-ième niveau du facteur B, \({\bar{Y}}_{r.}\) serait la moyenne marginale du r-ième niveau du facteur A, \({\bar{Y}}_{.c}\) serait la moyenne marginale du c-ième niveau du facteur B, et \({\bar{Y}}_{..}\) est la moyenne générale. En d’autres termes, les moyennes de notre échantillon peuvent être organisées dans le même tableau que les moyennes de population. Pour les données de nos essais cliniques, ce tableau ressemble à ceci :

Et si nous regardons les moyennes de l’échantillon que j’ai montré plus tôt, nous avons \({\bar{Y}}_{11} = 0,30\),\({\bar{Y}}_{12} = 0,60\) etc. Dans notre exemple d’essai clinique, le facteur drug a 3 niveaux et le facteur therapy a 2 niveaux, et ce que nous essayons d’exécuter est une ANOVA factorielle 3 x 2. Cependant, pour être un peu plus général, disons que le Facteur A (le facteur de ligne) a R niveaux et que le Facteur B (le facteur de colonne) a C niveaux , et donc ce que nous faisons ici est une ANOVA factorielle R x C.

Maintenant que nous avons rectifié notre notation, nous pouvons calculer la somme des carrés pour chacun des deux facteurs d’une manière relativement familière. Pour le facteur A, la somme des carrés entre les groupes est calculée en évaluant dans quelle mesure les moyennes marginales (ligne) \({\bar{Y}}_{1.},\ {\bar{Y}}_{2.}\) etc., sont différentes de la moyenne générale\({\bar{Y}}_{\text{..}}\). Nous procédons de la même manière que pour l’analyse de variance à sens unique : nous calculons la somme de la différence au carré entre les valeurs de \({\bar{Y}}_{i.}\) et de \({\bar{Y}}_{..}\). Plus précisément, s’il y a N personnes dans chaque groupe, alors nous calculons ceci

\[ \text{SS}_{A} = (N \times C)\sum_{r = 1}^{R}\left( {\bar{Y}}_{\text{r.}} - {\bar{Y}}_{\text{..}} \right)^{2} \]

Comme pour l’ANOVA à un facteur, la partie la plus intéressante¹²⁴ de cette formule est \(\left( {\bar{Y}}_{r.} - {\bar{Y}}_{..} \right)^{2}\), qui correspond à l’écart quadratique associé au niveau r. Tout ce que fait cette formule est de calculer cet écart au carré pour tous les niveaux R du facteur, de les additionner, puis de multiplier le résultat par N x C. La raison de cette dernière partie est qu’il y a plusieurs cellules dans notre plan qui ont le niveau r du facteur A. En fait, il y en a C, une pour chaque niveau possible du facteur B ! Ainsi, dans notre exemple, il y a deux cellules différentes dans le plan correspondant au médicament anxifree : une pour les personnes no therapy et une pour le groupe CBT. De plus, à l’intérieur de chacune de ces cellules, il y a N observations. Ainsi, si nous voulons convertir notre valeur SS en une quantité qui détermine la somme des carrés entre les groupes pour « chaque observation », nous devons multiplier par N x C. La formule pour le facteur B est bien sûr la même, mais avec des indices remplacés.

\[ \text{SS}_{B} = (N \times R)\sum_{c = 1}^{C}\left( {\bar{Y}}_{\text{.c}} - {\bar{Y}}_{\text{..}} \right)^{2} \]

Maintenant que nous disposons de ces formules, nous pouvons les comparer à la sortie Jamovi du fichier section précédente. Une fois de plus, un tableur est utile pour ce genre de calculs, alors n’hésitez pas à vous lancer. Vous pouvez également consulter la version que j’ai faite dans Excel dans le fichier clinicaltrial_factorialanova.xls.

Tout d’abord, calculons la somme des carrés associés à l’effet principal de la variable drug. Il y a un total de N = 3 personnes dans chaque groupe et C = 2 types de thérapie différents. Ou, pour le dire autrement, il y a 3 x 2 = 6 personnes qui ont reçu un médicament en particulier. Lorsque nous faisons ces calculs dans un tableur, nous obtenons une valeur de 3,45 pour la somme des carrés associés à l’effet principal de drug. Il n’est donc pas surprenant que ce chiffre soit le même que celui que vous obtenez lorsque vous recherchez la valeur SS pour le facteur drug dans le tableau ANOVA que j’ai présenté plus tôt, à la Figure 14‑3.

Nous pouvons répéter le même type de calcul pour l’effet de la thérapie. Encore une fois il y a N = 3 personnes dans chaque groupe, mais puisqu’il y a R = 3 médicaments différents, cette fois-ci on note qu’il y a 3 X 3 = 9 personnes qui ont reçu la CBT et 9 autres personnes qui ont reçu le placebo. Ainsi, notre calcul dans ce cas nous donne une valeur de 0,47 pour la somme des carrés associés à l’effet principal de therapy. Encore une fois, nous ne sommes pas surpris de constater que nos calculs sont identiques à ceux de l’analyse de variance dans la Figure 14‑3.

C’est donc ainsi que vous calculez les valeurs SS pour les deux effets principaux. Ces valeurs SS sont analogues à la somme des valeurs des carrés entre les groupes que nous avons calculées lors de l’analyse de variance à sens unique au chapitre 13. Cependant, ce n’est plus une bonne idée de les considérer comme des valeurs SS inter groupes, simplement parce que nous avons deux variables de groupement différentes et qu’il est facile de se tromper. Cependant, pour construire un test F, nous devons également calculer la somme des carrés à l’intérieur d’un groupe. Conformément à la terminologie que nous avons utilisée dans le chapitre sur la régression (chapitre 12) et à la terminologie utilisée par Jamovi lors de création du tableau ANOVA, je commencerai par faire référence à la valeur SS à l’intérieur des groupes comme la somme résiduelle des carrés SSR.

La façon la plus simple de comprendre les valeurs résiduelles de la SS dans ce contexte, je pense, est de d’imaginer qu’il s’agit de la variation résiduelle de la variable résultats après avoir pris en compte les différences dans les moyennes marginales (c.-à-d. après avoir enlevé le SSA et le SSB). Ce que je veux dire par là, c’est que nous pouvons commencer par calculer la somme totale des carrés, que j’appellerai SST. La formule est à peu près la même que pour l’ANOVA à un facteur. Nous prenons la différence entre chaque observation Yrci et la grande moyenne \[{\bar{Y}}_{\text{..}}\] .Elevez au carré les différences et additionnez-les toutes.

\[ \text{SS}_{T} = \sum_{r = 1}^{R}{\sum_{c = 1}^{C}{\sum_{i = 1}^{N}{(Y_{\text{rci}} - {\bar{Y}}_{\text{..}})}^{2}}} \]

La « triple sommation » semble ici plus compliquée qu’elle ne l’est. Dans les deux premières sommations, nous additionnons tous les niveaux du facteur A (c.-à-d. toutes les lignes r possibles de notre tableau) et tous les niveaux du facteur B (c.-à-d. toutes les colonnes c possibles). Chaque combinaison rc correspond à un seul groupe et chaque groupe contient N personnes, nous devons donc faire la somme de toutes ces personnes (c’est-à-dire toutes les valeurs i) également. En d’autres termes, tout ce que nous faisons ici est de faire la somme pour toutes les observations de l’ensemble de données (c.-à-d. toutes les combinaisons rci possibles).

A ce stade, nous connaissons la variabilité totale de la variable de résultat SST, et nous savons quelle part de cette variabilité peut être attribuée au facteur A (SSA) et quelle part peut être attribuée au facteur B (SSB). La somme résiduelle des carrés est donc définie comme étant la variabilité en Y qui ne peut être attribuée à aucun de nos deux facteurs. En d’autres termes

\[ \text{SS}_{R} = \text{SS}_{T} - (\text{SS}_{A} + \text{SS}_{B}) \]

Bien sûr, il existe une formule que vous pouvez utiliser pour calculer directement la SS résiduelle, mais je pense qu’il est plus conceptuel de la considérer comme ceci. L’intérêt d’appeler cela un résidu, c’est qu’il s’agit d’une variation résiduelle, et la formule ci-dessus l’indique clairement. Il convient également de noter que, conformément à la terminologie utilisée dans le chapitre sur la régression, il est courant de parler de SS_A + SS_B comme étant la variance attribuable au « modèle d’ANOVA », noté SS_M, on peut ainsi dire que la somme des carrés totale est égale à la somme des carrés du modèle plus la somme des carrés résiduelle. Plus loin dans ce chapitre, nous verrons qu’il ne s’agit pas seulement d’une similitude de surface : ANOVA et régression sont au fond la même chose.

Quoi qu’il en soit, il vaut probablement la peine de prendre un moment pour vérifier que nous pouvons calculer le SSR à l’aide de cette formule et vérifier que nous obtenons la même réponse que celle produite par Jamovi dans son tableau d’ANOVA. Les calculs sont assez simples lorsqu’ils sont effectués dans un tableur (voir le fichier clinicaltrial_factorialanova.xls). Nous pouvons calculer la SS totale à l’aide des formules ci-dessus (pour obtenir une SS totale = 4,85) et ensuite la SS résiduelle (= 0,92). Encore une fois, nous obtenons la même réponse.

14.1.4 Quels sont nos degrés de liberté ?

Les degrés de liberté sont calculés de la même manière que pour l’ANOVA à un facteur. Pour un facteur donné, les degrés de liberté sont égaux au nombre de niveaux moins 1 (c.-à-d. R - 1 pour la variable de ligne Facteur A et C - 1 pour la variable de colonne Facteur B). Ainsi, pour le facteur drug on obtient df = 2, et pour le facteur thérapeutique on obtient df = 1. Plus loin, lorsque nous discuterons de l’interprétation d’ANOVA comme modèle de régression (voir la section 14.6), je donnerai un énoncé plus clair de la façon dont nous en arrivons à ce chiffre. Mais pour l’instant, nous pouvons utiliser la simple définition des degrés de liberté, à savoir que les degrés de liberté sont égaux au nombre de quantités observées, moins le nombre de contraintes. Ainsi, pour le facteur drug, nous observons 3 moyennes de groupe distinctes, mais celles-ci sont limitées par 1 grande moyenne, et donc les degrés de liberté sont de 2. Pour les résidus, la logique est similaire, mais pas tout à fait la même. Le nombre total d’observations dans notre expérience est de 18. Les contraintes correspondent à 1 grande moyenne, les 2 moyennes de groupes supplémentaires que le facteur drug introduit, et 1 moyenne de groupe supplémentaire pour le facteur therapy, donc notre nombre de degrés de liberté est de 14. Nous avons comme formule N-1-(R-1)-(C-1), qui se simplifie en N-R-C+1.

14.1.5 ANOVA factorielle par opposition aux ANOVA à un facteur

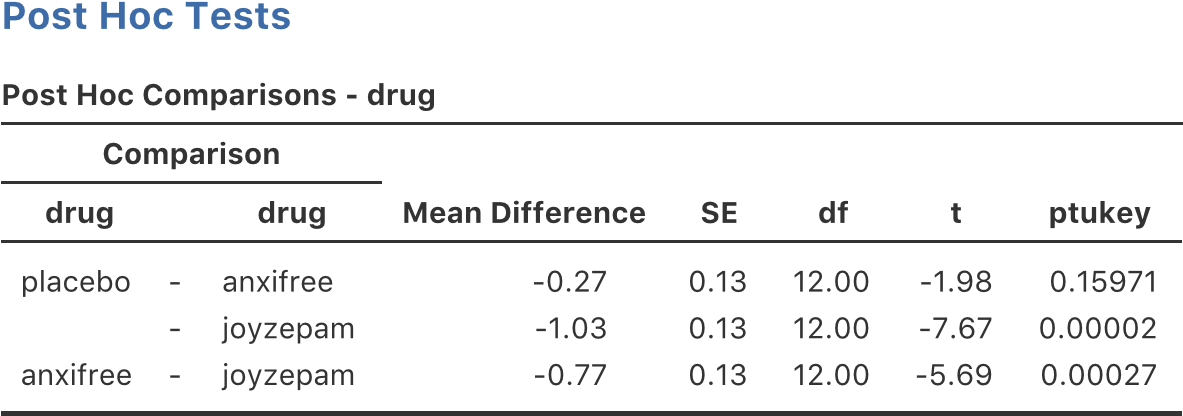
Maintenant que nous avons vu comment fonctionne une ANOVA factorielle, il vaut la peine de prendre un moment pour la comparer aux résultats des analyses à un facteur, car cela nous donnera une très bonne idée de la raison pour laquelle l’ANOVA factorielle est intéressante. Au chapitre 13, j’ai effectué une analyse de variance à un facteur pour voir s’il y avait des différences entre les médicaments, et une deuxième analyse de variance à un facteur pour voir s’il y avait des différences entre les traitements. Comme nous l’avons vu à la section 14.1.1, les hypothèses nulles et alternatives testées par les ANOVA à un facteur sont en fait identiques aux hypothèses testées par l’ANOVA factorielle. En regardant encore plus attentivement les tableaux ANOVA, on constate que la somme des carrés associés aux facteurs est identique dans les deux analyses (3,45 pour drug et 0,92 pour therapy), tout comme les degrés de liberté (2 pour drug, 1 pour therapy). Mais ils ne donnent pas les mêmes réponses ! Plus particulièrement, lorsque nous avons utilisé l’analyse de variance à un facteur pour therapy à la section 13.10, nous n’avons pas trouvé d’effet significatif (la valeur p était de .21). Cependant, quand on regarde l’effet principal de therapy dans le contexte de l’ANOVA bifactorielle, on obtient un effet significatif (p=.019). Les deux analyses ne sont manifestement pas les mêmes.

Pourquoi cela se produit-il ? Pour répondre, il faut comprendre comment les résidus sont calculés. Rappelons que l’idée derrière un test F est de comparer la variabilité qui peut être attribuée à un facteur particulier avec la variabilité qui ne peut être prise en compte (les résidus). Si vous utilisez une ANOVA à un facteur pour therapy, et que vous ignorez donc l’effet de drug, l’ANOVA comptabilisera toute la variabilité induite par drug dans les résidus ! Cela a pour effet de d’introduire plus de bruit dans les données qu’il n’y en a en réalité, et l’effet de therapy qui s’avère à juste titre significatif dans l’ANOVA bifactorielle devient maintenant non significatif. Si nous ignorons quelque chose qui compte vraiment (p. ex., le facteur drug) lorsque nous essayons d’évaluer la contribution d’autre chose (p. ex., le facteur therapy), notre analyse sera faussée. Bien sûr, il est tout à fait normal d’ignorer les variables qui ne sont pas vraiment pertinentes pour le phénomène d’intérêt. Si nous avions enregistré la couleur des murs et que cela se soit avéré être un facteur non important dans une analyse de variance à trois facteurs, il serait tout à fait acceptable de ne pas en tenir compte et de signaler simplement l’analyse de variance à deux facteurs plus simple qui ne comprend pas ce facteur non pertinent. Ce que vous ne devriez pas faire, c’est laisser tomber les variables qui font vraiment une différence !

14.1.6 Quels types de résultats cette analyse saisit-elle ?

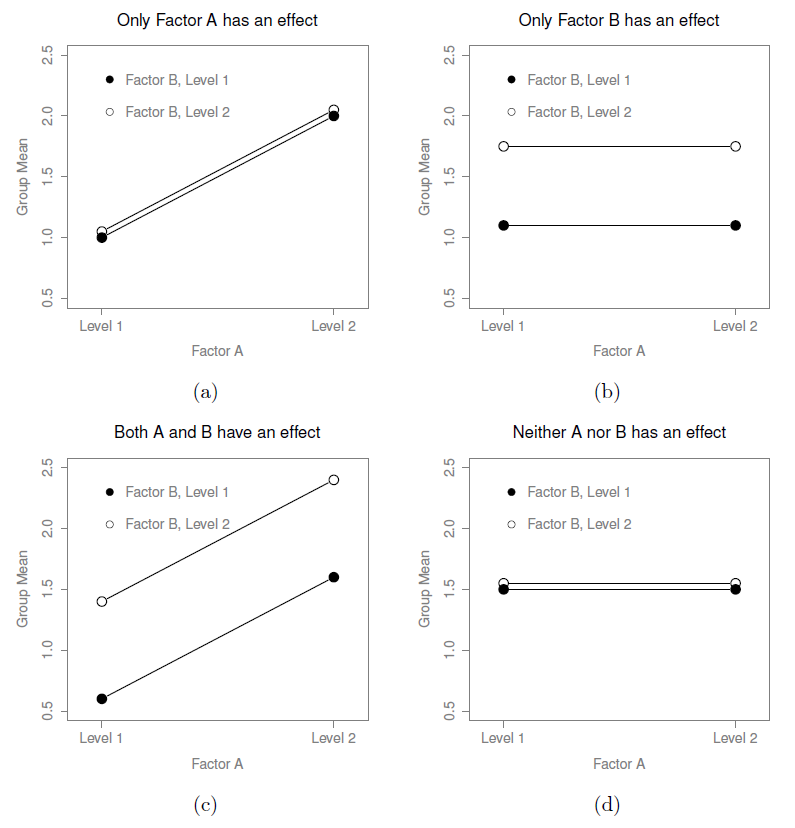
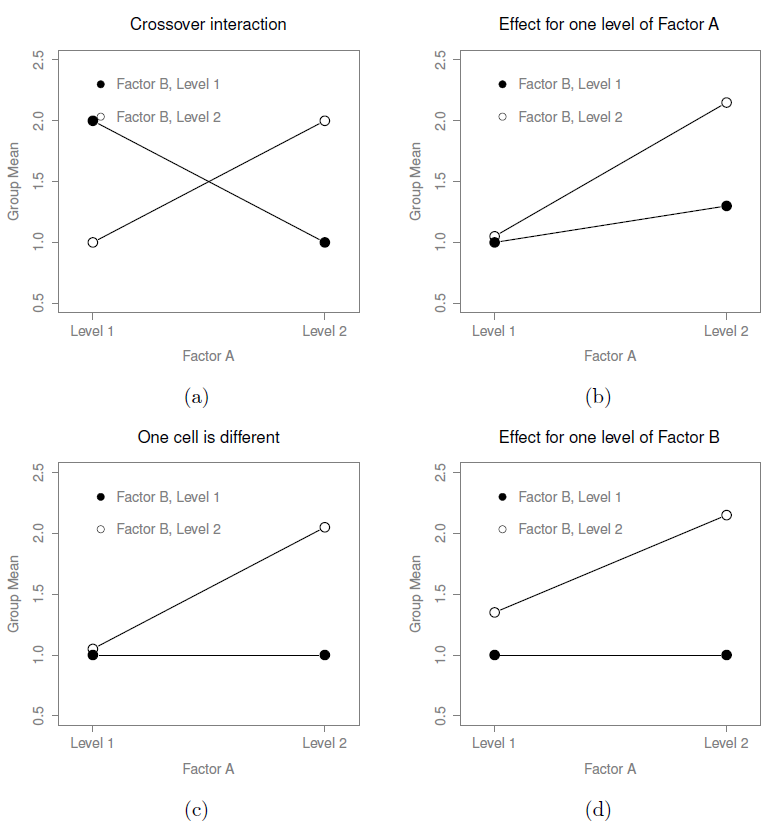
Le modèle ANOVA dont nous avons parlé jusqu’à présent couvre une gamme de modèles différents que nous pourrions observer dans nos données. Par exemple, dans une conception ANOVA bifactorielle, il y a quatre possibilités : (a) seul le facteur A compte, (b) seul le facteur B compte, (c) à la fois le facteur A et le facteur B compte, et (d) ni A ni B ne comptent. Un exemple de chacune de ces quatre possibilités est présenté à la Figure 14‑4.

14.2 ANOVA Factorielle 2 : conceptions équilibrées, interactions permises

Les quatre modèles de données présentés à la Figure 14‑4 sont tous très réalistes. Il existe un grand nombre d’ensembles de données qui produisent exactement ces tendances. Cependant, ils ne représentent pas toute l’histoire et le modèle ANOVA dont nous avons parlé jusqu’à présent ne suffit pas à rendre pleinement compte d’un tableau des moyennes de groupe. Pourquoi pas ? Pourquoi pas ? Eh bien, jusqu’à présent, nous avons la possibilité de parler de l’idée que les drogues peuvent influencer l’humeur, et la thérapie peut influencer l’humeur, mais pas la possibilité d’une interaction entre les deux. On dit qu’une interaction entre A et B se produit lorsque l’effet du facteur A est différent, selon le niveau du facteur B dont il est question. Plusieurs exemples d’un effet d’interaction avec le contexte d’une ANOVA 2ˆ2 sont présentés à la Figure 14‑5. Pour donner un exemple plus concret, supposons que le fonctionnement d’Anxifree et Joyzepam est régi par des mécanismes physiologiques très différents. L’une des conséquences de cette situation est que bien que Joyzepam ait plus ou moins le même effet sur l’humeur, que l’on soit en thérapie ou non, Anxifree est en fait beaucoup plus efficace lorsqu’il est administré conjointement avec la TCC.

Figure 14‑4 : Les quatre résultats différents d’une 2 x 2 ANOVA en l’absence d’interaction. Dans la figure (a), nous voyons un effet principal du facteur A et aucun effet du facteur B. La figure (b) montre un effet principal du facteur B mais aucun effet du facteur A. La figure (c) montre des effets principaux du facteur A et du facteur B. Enfin, la figure (d) ne montre aucun effet des deux facteurs.

Figure 14‑5 : Des interactions qualitativement différentes pour une 2 x 2 ANOVA

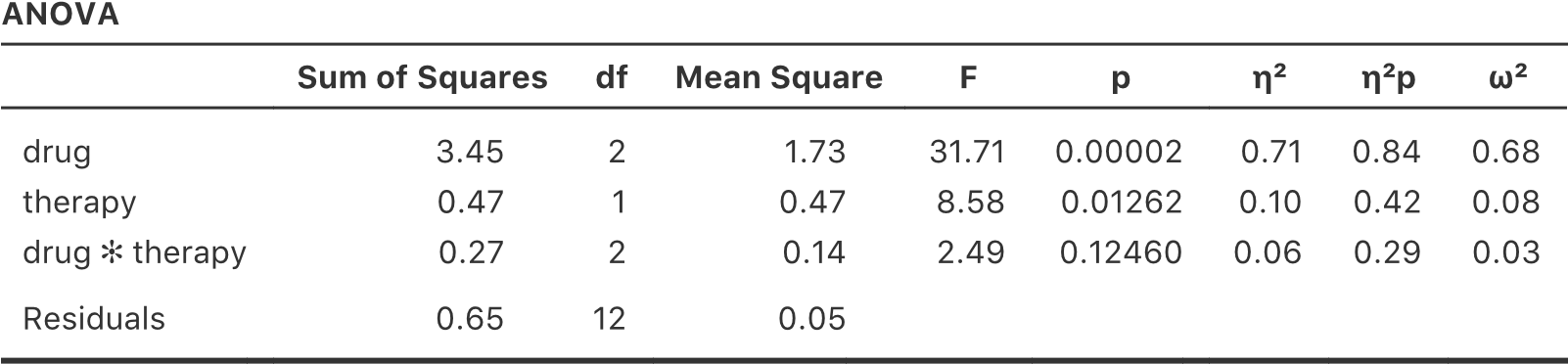
L’analyse de variance que nous avons élaborée dans la section précédente ne tient pas compte de cette idée. Pour se faire une idée de la réalité d’une interaction ici, il est utile de tracer les différentes moyennes de groupe. Dans le Jamovi, cela se fait via l’option « Descriptive Plots » de l’ANOVA - il suffit de déplacer le facteur drug dans la case « Horizontal axis », et de déplacer therapy dans la case « Separate Lines ». Ceci devrait ressembler à la Figure 14‑6. Notre principale préoccupation concerne le fait que les deux lignes ne sont pas parallèles. L’effet de la CBT (différence entre la ligne pleine et la ligne pointillée) lorsque le médicament est le Joyzepam (côté droit) semble être près de zéro, encore plus petit que l’effet de la CBT lorsqu’un placebo est utilisé (côté gauche). Cependant, lorsqu’Anxifree est administré, l’effet de la CBT est plus important que celui du placebo (milieu). Cet effet est-il réel ou s’agit-il d’une variation aléatoire due au hasard ? Notre analyse de variance originale ne peut pas répondre à cette question, car nous ne tenons pas compte de l’idée que les interactions existent même ! Dans cette section, nous allons régler ce problème.

Figure 14‑6 : copie d’écran Jamovi montrant comment générer un diagramme d’interaction descriptif dans ANOVA en utilisant les données des essais cliniques

14.2.1 Qu’est-ce qu’un effet d’interaction ?

L’idée clé que nous allons introduire dans cette section est celle d’un effet d’interaction. Dans le modèle ANOVA que nous avons examiné jusqu’à présent, il n’y a que deux facteurs en cause dans notre modèle (c.-à-d. drug et la therapy). Mais lorsque nous ajoutons une interaction, nous ajoutons une nouvelle composante au modèle : la combinaison de drug et de therapy. Intuitivement, l’idée derrière un effet d’interaction est assez simple. Cela signifie simplement que l’effet du facteur A est différent selon le niveau du facteur B dont nous parlons. Mais qu’est-ce que cela signifie réellement en termes de données ? Le graphique de la Figure 14‑5 illustre plusieurs modèles qui, bien que très différents les uns des autres, seraient tous considérés comme un effet d’interaction. Il n’est donc pas tout à fait simple de traduire cette idée qualitative en une notion mathématique avec laquelle un statisticien peut travailler.

Par conséquent, la façon dont l’idée d’un effet d’interaction est formalisée en termes d’hypothèses nulles et alternatives est un peu difficile, et je suppose que beaucoup de lecteurs de ce livre ne seront probablement pas très intéressés. Néanmoins, je vais essayer de donner l’idée de base ici.

Pour commencer, nous devons être un peu plus explicites sur nos principaux effets. Considérons l’effet principal du facteur A (drug dans notre exemple courant). Nous avons initialement formulé cette hypothèse en fonction de l’hypothèse nulle que les deux moyennes marginales \(\mu_{r.}\) sont égales l’une à l’autre. Évidemment, si toutes ces valeurs sont égales les unes aux autres, alors elles doivent aussi être égales à la grande moyenne \(\mu_{..}\) On peut donc définir l’effet du facteur A au niveau r comme étant égal à la différence entre la moyenne marginale \(\mu_{r}\) et la moyenne générale \(\mu_{..}\). Signalons cet effet par \(\alpha_{r}\), et notons que

\[ \alpha_{r} = \mu_{r.} - \mu_{..} \]

Maintenant, par définition, la somme de toutes les valeurs de \(\alpha_{r}\) doivent être égales à zéro, pour la même raison que la moyenne des moyennes marginales \(\mu_{r.}\) doit être égale à la grande moyenne \(\mu_{..}\). De même, nous pouvons définir l’effet du facteur B au niveau i comme étant la différence entre la moyenne marginale de la colonne \(\mu_{.c}\) et la moyenne générale \(\mu_{..}\)

\[ \beta_{c} = \mu_{.c} - \mu_{..} \]

et une fois de plus, la somme de ces valeurs de \(\beta_{c}\) doit être égale à zéro. Les statisticiens aiment parfois parler des principaux effets avec ces valeurs \(\alpha_{r}\) et \(\beta_{c}\) car cela leur permet d’être précis sur ce que signifie il n’y a aucun effet d’interaction. S’il n’y a aucune interaction, alors ces valeurs \(\alpha_{r}\) et \(\beta_{c}\) décrivent parfaitement le la moyenne de groupe \(\mu_{rc}\). Plus précisément, cela signifie que

\[ u_{rc} = u_{..} + \alpha_{r} + \beta_{c} \]

En d’autres termes, il n’y a rien de particulier pour à propos des moyennes de groupe que vous ne pourriez pas prédire parfaitement en connaissant tous les moyennes marginales. Et c’est notre hypothèse nulle, justement. L’hypothèse alternative est que

\[ u_{rc} \neq u_{..} + \alpha_{r} + \beta_{c} \]

pour au moins un groupe rc dans notre tableau. Cependant, les statisticiens aiment souvent écrire cela un peu différemment. Ils définiront habituellement l’interaction spécifique associée au groupe rc comme étant un certain nombre, maladroitement appelé \(\left( \alpha\beta \right)_{rc}\), puis ils diront que l’hypothèse alternative est que

\[ u_{rc} = u_{..} + \alpha_{r} + \beta_{c} + \left( \alpha\beta \right)_{rc} \]

où \(\left( \alpha\beta \right)_{rc}\) est différent de zéro pour au moins un groupe. Cette notation est plutôt moche à regarder, mais elle est pratique comme nous le verrons dans la prochaine section lorsque nous discuterons de la façon de calculer la somme des carrés.

14.2.2 Calcul des sommes de carrés pour l’interaction

Comment calculer la somme des carrés des termes d’interaction, SS_A:B ? Eh bien, tout d’abord, il est utile de noter comment la section précédente a défini l’effet d’interaction en fonction de la mesure de la différence entre les moyennes réelles du groupe et ce à quoi on pourrait s’attendre en regardant simplement les moyennes marginales. Bien sûr, toutes ces formules font référence à des paramètres de population plutôt qu’à des statistiques d’échantillonnage, de sorte que nous ne savons pas vraiment ce qu’elles sont. Cependant, nous pouvons les estimer en utilisant des moyennes d’échantillonnage au lieu des moyennes de population. Ainsi, pour le facteur A, une bonne façon d’estimer l’effet principal au niveau r est la différence entre la moyenne marginale \({\bar{Y}}_{rc}\) de l’échantillon et la moyenne générale \({\bar{Y}}_{..}\) . En d’autres termes, nous utiliserions ceci comme notre estimation de l’effet

\[ {\hat{\alpha}}_{r} = {\bar{Y}}_{r.} - {\bar{Y}}_{..} \]

De la même façon, notre estimation de l’effet principal du facteur B au niveau c peut être définie comme suit

\[ {\hat{\beta}}_{c} = {\bar{Y}}_{.c} - {\bar{Y}}_{..} \]

Maintenant, si vous revenez aux formules que j’ai utilisées pour décrire les valeurs SS pour les deux effets principaux, vous remarquerez que ces termes d’effets sont exactement les quantités que nous avons élevées au carré et additionnées ! Alors, quel est l’analogie de ceci pour les termes d’interaction ? La réponse à cette question peut être trouvée en réarrangeant d’abord la formule de ma moyenne \(\mu_{rc}\) pour le groupe sous l’hypothèse alternative, donc

\[\begin{aligned} \left( \alpha\beta \right)_{rc} &= \mu_{rc} - \mu_{..} - \alpha_{.r} - \beta_{c}\\ &= \mu_{rc} - \mu_{..} - \left( \mu_{r.} - \mu_{..} \right) - \left( \mu_{.c} - \mu_{..} \right)\\ &= \mu_{rc} - \mu_{r.} - \mu_{.c} + \mu_{..} \end{aligned} \]

Donc, encore une fois, si nous substituons nos statistiques d’échantillon à la moyenne de la population, nous obtenons ce qui suit comme estimation de l’effet d’interaction pour le groupe rc,

\[ \left( \hat{\alpha\beta} \right)_{\text{rc}} = {\bar{Y}}_{\text{rc}} - {\bar{Y}}_{\text{r.}} - {\bar{Y}}_{\text{.c}} + {\bar{Y}}_{\text{..}} \]

Il ne nous reste plus qu’à additionner toutes ces estimations pour tous les niveaux R du facteur A et tous les niveaux C du facteur B, et nous obtenons la formule suivante pour la somme des carrés associés à l’interaction dans son ensemble

\[ \text{SS}_{A:B} = N\sum_{r = 1}^{R}{\sum_{c = 1}^{C}\left( {\bar{Y}}_{\text{rc}} - {\bar{Y}}_{\text{r.}} - {\bar{Y}}_{\text{.c}} + {\bar{Y}}_{\text{..}} \right)^{2}} \]

où nous multiplions par N parce qu’il y a N observations dans chacun des groupes, et nous voulons que nos valeurs SS reflètent la variation entre les observations expliquées par l’interaction, et non la variation entre groupes.

Maintenant que nous avons une formule pour calculer SS_A:B, il est important de reconnaître que le terme d’interaction fait partie du modèle (bien sûr), donc la somme totale des carrés associés au modèle, SS_M, est maintenant égale à la somme des trois valeurs SS pertinentes, SS_A + SS_B + SS_A:B. La somme résiduelle des carrés SSR est toujours définie comme la variation restante, à savoir SS_T-SS_M, mais maintenant que nous avons le terme d’interaction cela devient

\[ \text{SS}_{R} = \text{SS}_{T} - \left( \text{SS}_{A} + \text{SS}_{B} + \text{SS}_{A:B} \right) \]

Par conséquent, la somme résiduelle des carrés SSR sera plus petite que dans notre ANOVA originale qui ne comprenait pas les interactions

14.2.3 Degrés de liberté pour l’interaction

Le calcul des degrés de liberté pour l’interaction est, une fois de plus, légèrement plus délicat que le calcul correspondant pour les effets principaux. Pour commencer, pensons au modèle ANOVA dans son ensemble. Une fois que nous incluons les effets d’interaction dans le modèle, nous permettons à chaque groupe d’avoir une moyenne unique, \(\mu_{rc}\). Pour une ANOVA factorielle R x C, cela signifie qu’il y a R x C quantités d’intérêt dans le modèle et qu’il n’y a qu’une seule contrainte : toutes les moyennes du groupe doivent être égales à la moyenne générale. Ainsi, le modèle dans son ensemble doit avoir (R x C)-1 degrés de liberté. Mais l’effet principal du facteur A a R-1 degrés de liberté, et l’effet principal du facteur B a C-1 degrés de liberté. Cela signifie que les degrés de liberté associés à l’interaction sont les suivants

\[\begin{aligned} df_{A:B} &= \left( R \times C - 1 \right) - \left( R - 1 \right) - \left( C - 1 \right)\\ &= RC - C + 1\\ &= (R - C)(C - 1) \end{aligned} \]

qui n’est que le produit des degrés de liberté associés au facteur de ligne et au facteur de colonne.

Qu’en est-il des degrés de liberté résiduels ? Parce que nous avons ajouté des termes d’interaction qui absorbent certains degrés de liberté, il reste moins de degrés de liberté résiduels. Plus précisément, notez que si le modèle avec interaction a un total de (R x C)-1, et qu’il y a N observations dans votre ensemble de données qui sont contraintes de satisfaire 1 grande moyenne, vos degrés de liberté résiduels deviennent maintenant N-(R x C)-1+1, ou seulement N-(R x C).

14.2.4 Exécuter l’ANOVA dans Jamovi

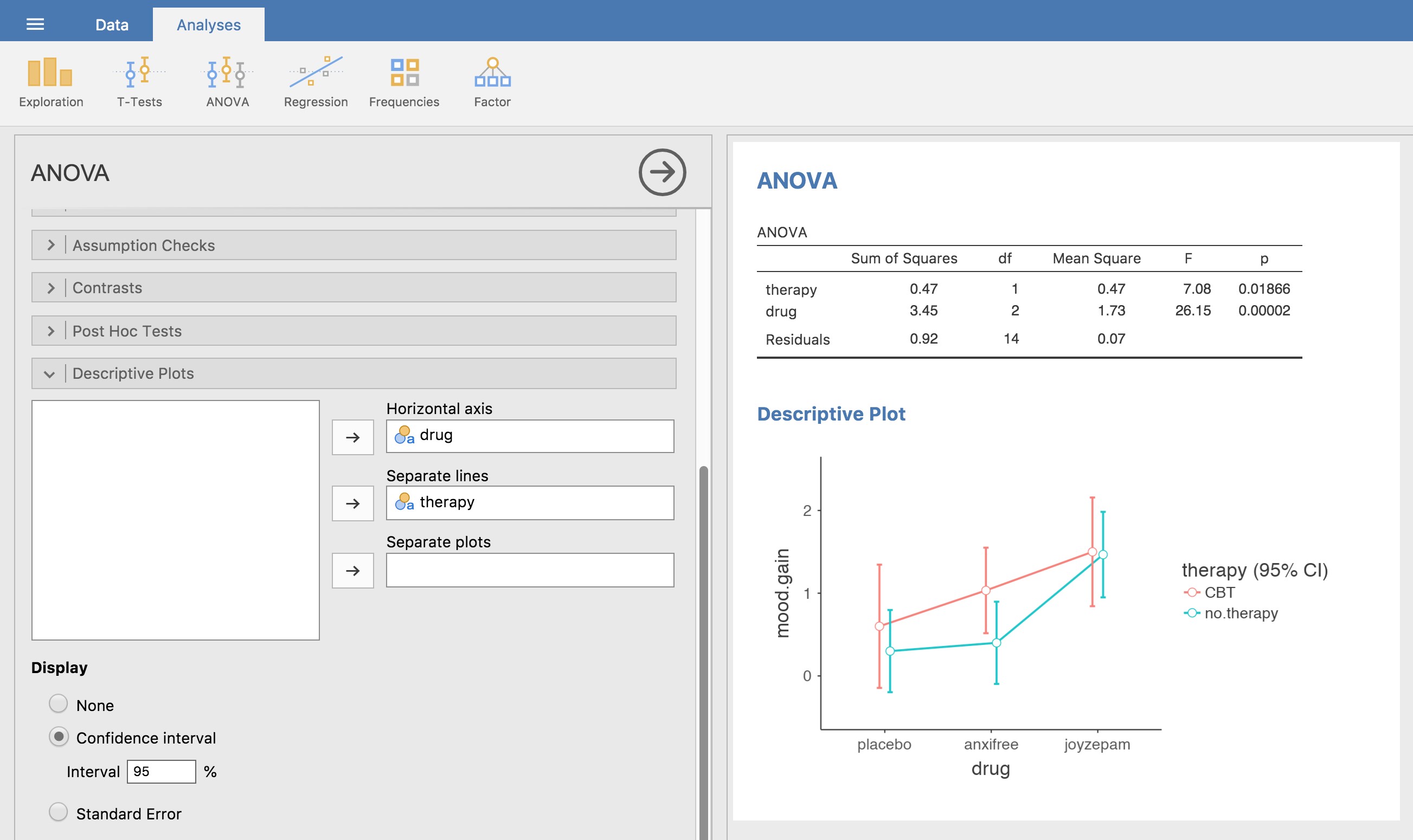
L’ajout de termes d’interaction au modèle ANOVA dans Jamovi est simple. En fait, c’est plus que simple parce que c’est l’option par défaut pour ANOVA. Cela signifie que lorsque vous spécifiez une ANOVA avec deux facteurs, par exemple drug et therapy, la composante d’interaction - drug*therapy - est automatiquement ajoutée au modèle¹²⁵. Lorsque nous exécutons l’analyse de variance avec le terme d’interaction inclus, nous obtenons les résultats présentés à la Figure 14‑7.

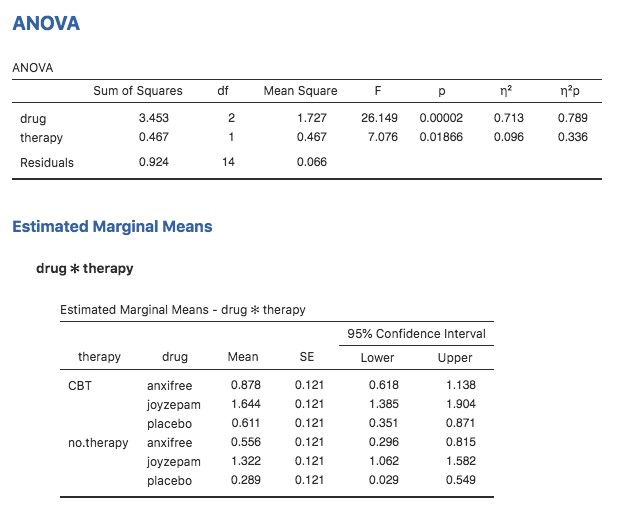
Il s’avère que, bien que nous ayons un effet principal significatif du médicament (F(2,12) = 31,7, p<.001) et le type de thérapie (F(1,12) = 8,6, p=.013), il n’y a aucune interaction significative entre les deux (F(2,12) = 2,5, p=0.125).

Figure 14‑7 : Résultats pour le modèle factoriel complet, y compris la composante d’interaction drug*therapy

14.2.5 Interprétation des résultats

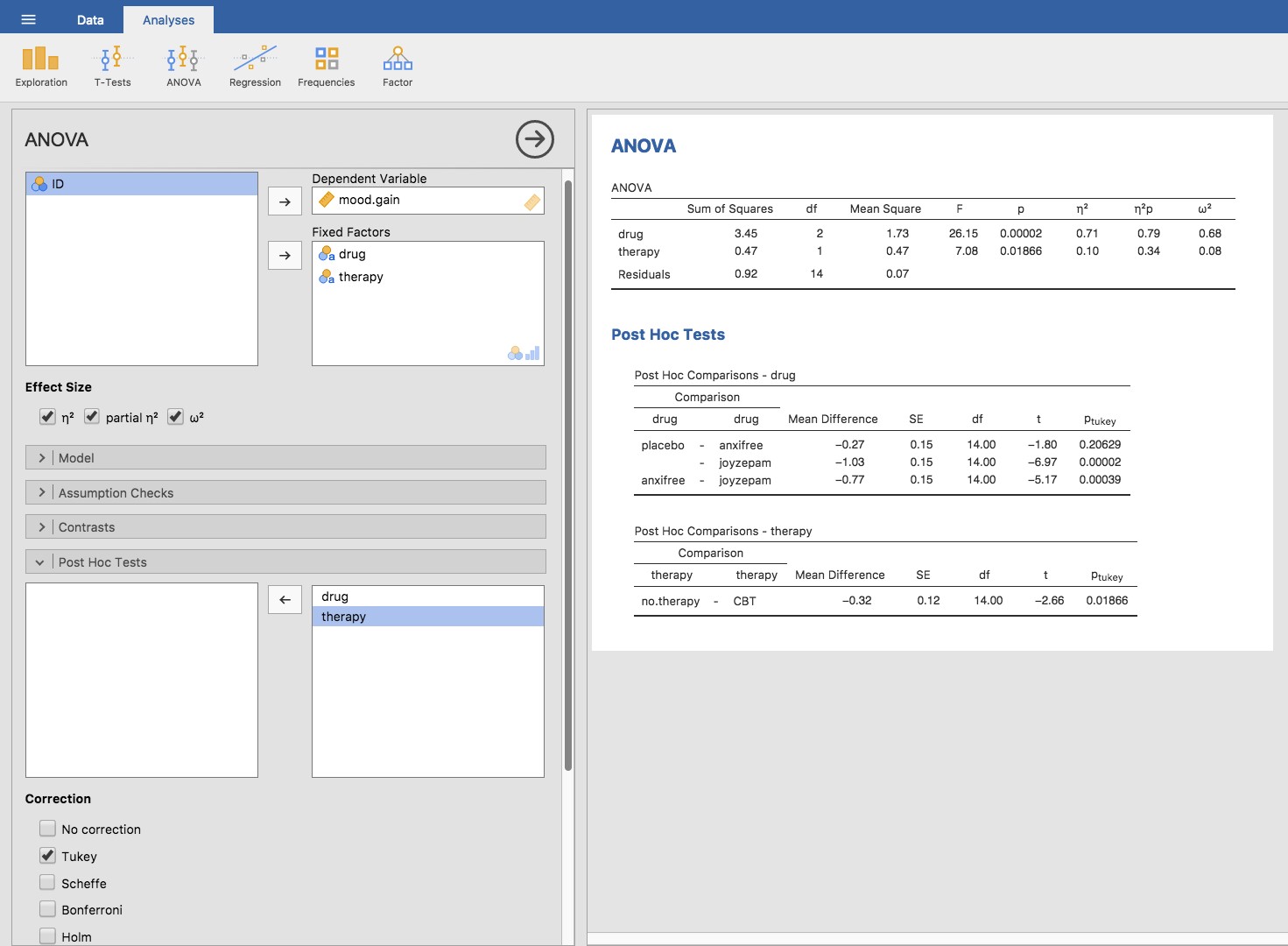
Il y a quelques éléments très importants à prendre en considération lors de l’interprétation des résultats de l’analyse de variance factorielle. Tout d’abord, il y a le même problème que nous avions avec l’analyse de variance à un facteur, si vous obtenez un effet principal important d’un facteur (disons) drug, cela ne vous dit rien sur les différences entre médicaments. Pour le savoir, vous devez exécuter des analyses supplémentaires. Nous parlerons de certaines analyses que vous pouvez exécuter dans les sections 14.7 et 14.8. Il en va de même pour les effets d’interaction. Savoir qu’il y a une interaction importante ne vous dit rien sur le type d’interaction qui existe. Encore une fois, vous devrez effectuer des analyses supplémentaires.

Deuxièmement, il y a un problème d’interprétation très particulier qui se pose lorsque vous obtenez un effet d’interaction significatif mais aucun effet principal correspondant. Cela arrive parfois. Par exemple, dans l’interaction croisée illustrée à la Figure 14‑5a, c’est exactement ce que vous trouverez. Dans ce cas, ni l’un ni l’autre des principaux effets ne serait significatif, mais l’effet d’interaction le serait. C’est une situation difficile à interpréter, et les gens sont souvent un peu confus. Le conseil général que les statisticiens aiment donner dans cette situation est que vous ne devriez pas accorder beaucoup d’attention aux effets principaux quand une interaction est présente. La raison en est que, bien que les tests des effets principaux soient parfaitement valables d’un point de vue mathématique, lorsqu’il y a un effet d’interaction significatif, les effets principaux testent rarement des hypothèses intéressantes. Rappelons, à la section 14.1.1, que l’hypothèse nulle pour un effet principal est que les moyennes marginales sont égales les unes aux autres et qu’une moyenne marginale est formée en faisant la moyenne de plusieurs groupes différents. Mais si vous avez un effet d’interaction significatif, vous savez que les groupes qui composent la moyenne marginale ne sont pas homogènes, alors le motif de l’intérêt pour ces moyennes marginales n’est pas vraiment évident.

Je tenais à le préciser. Encore une fois, restons-en à un exemple clinique. Supposons que nous ayons un plan 2x2 comparant deux thérapies différentes pour les phobies (p. ex. désensibilisation systématique vs exposition in vivo) et deux médicaments anti-anxiété différents (p. ex. Anxifree vs Joyzepam). Supposons maintenant que ce que nous avons découvert, c’est qu’Anxifree n’avait aucun effet lorsque la thérapie est la désensibilisation, et que Joyzepam n’avait aucun effet avec l’exposition in vivo. Mais les deux ont été assez efficaces pour l’autre thérapie. Il s’agit d’une interaction croisée classique, et ce que nous constatons en exécutant l’analyse de variance, c’est qu’il n’y a pas d’effet principal du médicament, mais une interaction significative. Maintenant, qu’est-ce que cela signifie de dire qu’il n’y a pas d’effet principal ? Eh bien, cela signifie que si nous faisons la moyenne sur les deux traitements psychologiques, alors l’effet moyen d’Anxifree et de Joyzepam est le même. Mais qui cela intéresse-t-il ? Lorsqu’on traite quelqu’un pour des phobies, il n’est jamais possible de traiter une personne en utilisant une « moyenne » d’exposition et de désensibilisation. Ça n’a pas beaucoup de sens. Soit vous avez l’un, soit l’autre. Pour un traitement, un médicament est efficace, et pour l’autre, c’est l’autre médicament qui est efficace. Ce qui importe, c’est l’interaction et l’effet principal n’a pas d’importance.

Ce genre de choses arrive souvent. Les principaux effets sont des tests de moyennes marginales, et lorsqu’une interaction est présente, nous trouvons souvent les moyennes marginales sans grand intérêt parce qu’elles impliquent de faire la moyenne des choses dont l’interaction nous dit de ne pas en faire la moyenne ! Bien sûr, il n’est pas toujours vrai qu’un effet principal n’a pas de sens lorsqu’une interaction est présente. Souvent, on peut obtenir un grand effet principal et une très petite interaction, auquel cas on peut encore dire des choses comme « le médicament A est généralement plus efficace que le médicament B » (parce qu’il y avait un grand effet du médicament), mais il faudrait le modifier un peu en ajoutant que « la différence d’efficacité était différente en fonction des différents traitements psychologiques ». Quoi qu’il en soit, le point principal ici est que chaque fois que vous obtenez une interaction significative, vous devriez vous arrêter et réfléchir à ce que l’effet principal signifie réellement dans ce contexte. Ne supposez pas automatiquement que l’effet principal est intéressant.

14.3 Taille de l’effet

Le calcul de la valeur de l’effet d’une ANOVA factorielle est assez semblable à celui d’une ANOVA à un facteur (voir section 13.4). Plus précisément, nous pouvons utiliser \(\eta^{2}\) (eta-carré) comme un moyen simple de mesurer la taille de l’effet global pour un terme donné. Comme précédemment, \(\eta^{2}\) est défini en divisant la somme des carrés associés à ce terme par la somme totale des carrés. Par exemple, pour déterminer l’ampleur de l’effet principal du facteur A, nous utiliserions la formule suivante :

\[ \eta^{2} = \frac{\text{SS}_{A}}{\text{SS}_{T}} \]

Comme précédemment, ceci peut être interprété de la même manière que R2 en régression.¹²⁶ Il vous indique la proportion de variance de la variable résultat qui peut être expliquée par l’effet principal du facteur A. Il s’agit donc d’un nombre qui varie de 0 (aucun effet du tout) à 1 (qui explique toute la variabilité du résultat). De plus, la somme des valeurs de \(\eta^{2}\) pour tous les termes du modèle est égale au R² total pour le modèle d’ANOVA. Si, par exemple, le modèle ANOVA est parfaitement adapté (c’est-à-dire qu’il n’y a aucune variabilité à l’intérieur des groupes !), la somme des valeurs \(\eta^{2}\) sera égale à 1. Bien sûr, cela arrive rarement, voire jamais, dans la vraie vie.

Cependant, lorsqu’on effectue une analyse de variance factorielle, il existe une deuxième mesure de la taille de l’effet que les gens aiment signaler, connue sous le nom de \(\eta^{2}\) partiel. L’idée qui sous-tend le \(\eta^{2}\) partiel (noté parfois \(_{p}^{}\eta^{2}\) ou \(\eta_{p}^{2}\)) est que, lorsqu’on mesure l’ampleur de l’effet pour un terme particulier (disons, l’effet principal du facteur A), on veut délibérément ignorer les autres effets du modèle (p. ex., l’effet principal du facteur B). C’est-à-dire, vous souhaiteriez faire semblant que l’effet de tous ces autres termes est nul afin de calculer ce que la valeur de \(\eta^{2}\) aurait été. C’est en fait assez facile à calculer. Tout ce que vous avez à faire est d’enlever la somme des carrés associés aux autres termes du dénominateur. En d’autres termes, si vous voulez l’effet principal du Facteur A sur \(\eta^{2}\), le dénominateur est juste la somme des carrés du Facteur A et des résidus.

\[ \text{partial }\eta_{A}^{2} = \frac{\text{SS}_{A}}{\text{SS}_{A} + \text{SS}_{R}} \]

Cela vous donnera toujours un nombre plus grand que \(\eta^{2}\), ce que le cynique que je suis soupçonne d’expliquer la popularité de \(\eta^{2}\) partiel. Et encore une fois, vous obtenez un nombre entre 0 et 1, où 0 représente aucun effet. Cependant, il est un peu plus difficile d’interpréter ce que signifie une grande valeur partielle de \(\eta^{2}\). En particulier, vous ne pouvez pas comparer les valeurs partielles de \(\eta^{2}\) d’un terme à l’autre ! Supposons, par exemple, qu’il n’y ait aucune variabilité à l’intérieur des groupes, dans ce cas, SSR = 0. Cela signifie que chaque terme a une valeur partielle \(\eta^{2}\) de 1. Mais cela ne signifie pas que tous les termes dans votre modèle sont également importants, ou même qu’ils sont aussi grands. Tout ce que cela signifie, c’est que tous les termes de votre modèle ont des valeurs d’effet qui sont importantes par rapport à la variation résiduelle. Elle n’est pas comparable d’un terme à l’autre.

Pour voir ce que j’entends par là, il est utile de voir un exemple concret. Examinons d’abord la taille de l’effet de l’analyse de variance originale sans le terme d’interaction, à la Figure 14‑3 :

	Eta.sq	Partial.eta.sq
drug	0,71	0,79
therapy	0,10	0,34

En regardant d’abord les valeurs de \(\eta^{2}\), on constate que drug représente 71 % de la variance (c.-à-d. \(\eta^{2}=0,71\)) pour la variable mood.gain, alors que le facteur therapy ne représente que 10 %. Cela laisse un total de 19 % de la variation non prise en compte (c.-à-d. que les résidus constituent 19 % de la variation du résultat). Dans l’ensemble, cela implique que nous avons un très grand effet de¹²⁷ drug et un effet modeste de therapy.

Regardons maintenant les valeurs partielles de \(\eta^{2}\), illustrées à la Figure 14‑3. Parce que l’effet de therapy n’est pas si important, le contrôle de l’effet ne fait pas beaucoup de différence, donc la valeur partielle \(\eta^{2}\) pour la variable drug n’augmente pas beaucoup, et on obtient une valeur de \(_{p}\eta^{2} = 0,79\). En revanche, parce que l’effet de drug était très important, la prise en compte de l’effet de drug fait une grande différence, et donc lorsque nous calculons la valeur partielle de \(\eta^{2}\) pour la variable therapy, vous pouvez voir qu’elle s’élève à \(_{p}\eta^{2}=0,34\). La question que nous devons nous poser est la suivante : que signifient réellement ces valeurs partielles de \(\eta^{2}\) ? La façon dont j’interprète généralement le \(\eta^{2}\) partiel pour l’effet principal du facteur A est de l’interpréter comme un énoncé au sujet d’une expérience hypothétique dans laquelle seul le facteur A était modifié. Ainsi, même si, dans cette expérience, nous avons deux facteurs A et B, nous pouvons facilement imaginer une expérience dans laquelle seul le facteur A utilisé, et la statistique partielle \(\eta^{2}\) vous indique quelle part de la variance de la variable résultat que vous vous attendriez à voir prise en compte dans cette expérience. Cependant, il faut noter que cette interprétation, comme beaucoup de choses associées aux effets principaux, n’a pas beaucoup de sens lorsqu’il y a un effet d’interaction important et significatif.

En parlant d’effets d’interaction, voici ce que nous obtenons lorsque nous calculons la taille de l’effet pour le modèle qui inclut le terme d’interaction, comme dans la Figure 14‑7. Comme vous pouvez le voir, les valeurs de \(\eta^{2}\) pour les effets principaux ne changent pas, contrairement aux valeurs partielles de \(\eta^{2}\) :

14.3.1 Moyenne estimée du groupe

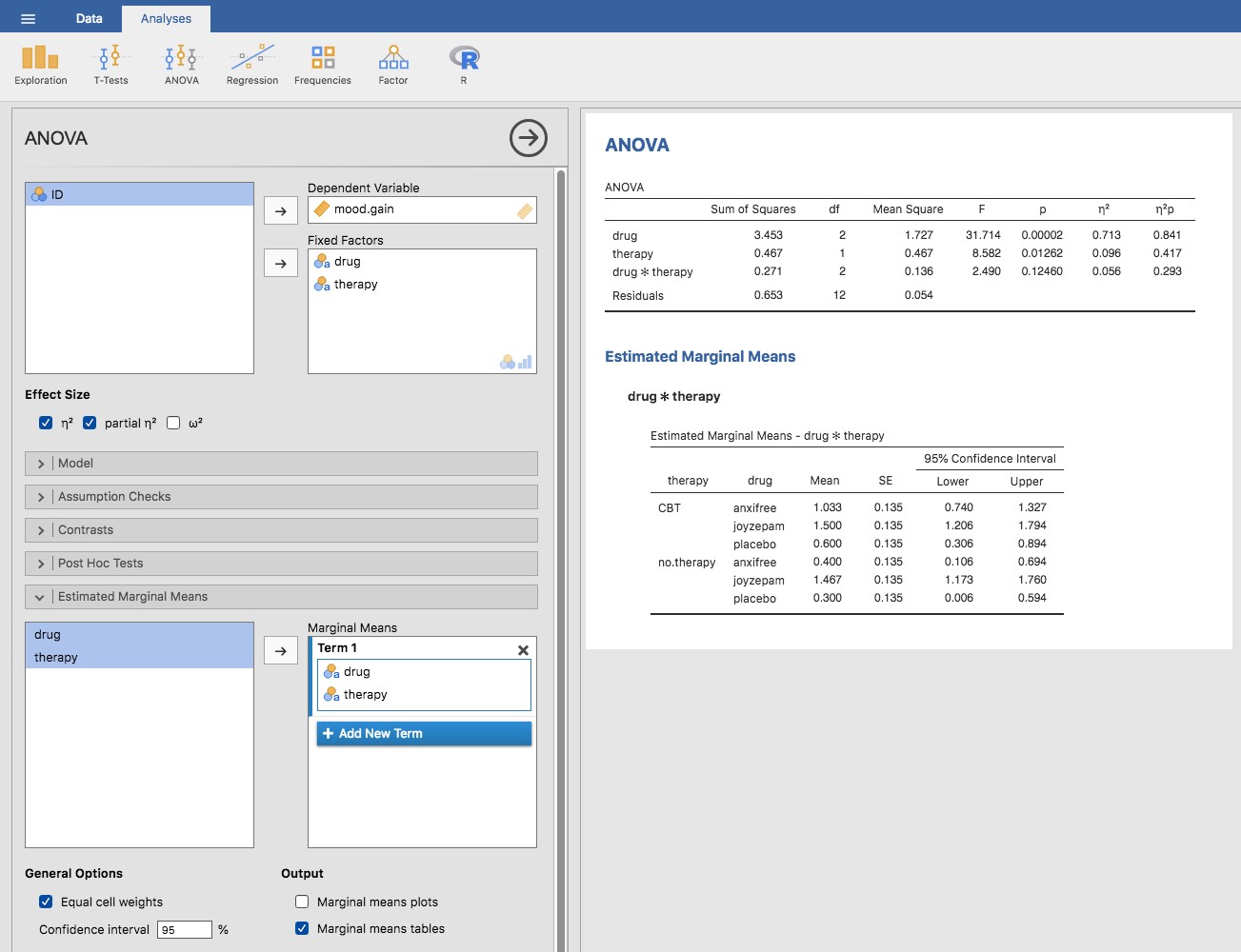
Dans de nombreuses situations, vous voudrez déclarer des estimations de toutes les moyennes de groupe en fonction des résultats de votre analyse de variance, ainsi que des intervalles de confiance qui y sont associés. Pour ce faire, vous pouvez utiliser l’option « Estimated Marginal Means » dans l’analyse ANOVA de Jamovi, comme dans la Figure 14‑8. Si l’analyse de variance que vous avez exécutée est un modèle saturé (c.-à-d. qu’elle contient tous les effets principaux possibles et tous les effets d’interaction possibles), les estimations des moyennes des groupes sont en fait identiques aux moyennes de l’échantillon, bien que les intervalles de confiance utilisent une estimation globale des erreurs types plutôt que des estimations distinctes pour chaque groupe.

Figure 14‑8 : capture d’écran de Jamovi montrant les moyennes marginales du modèle saturé, c’est-à-dire incluant la composante d’interaction, avec l’ensemble des données clinicaltrial

Les résultats montrent que le gain d’humeur moyen estimé pour le groupe placebo sans traitement était de 0,300, avec un intervalle de confiance à 95 % allant de 0,006 à 0,594. Il est à noter qu’il ne s’agit pas des mêmes intervalles de confiance que ceux que vous obtiendriez si vous les calculiez séparément pour chaque groupe, parce que le modèle ANOVA suppose l’homogénéité de la variance et utilise donc une estimation globale de l’écart type.

Lorsque le modèle ne contient pas le terme d’interaction, la moyenne estimée du groupe sera différente de la moyenne de l’échantillon. Au lieu de déclarer la moyenne de l’échantillon, Jamovi calculera la valeur de la moyenne du groupe à partir de la moyenne marginale (c.-à-d. en supposant qu’il n’y a aucune interaction). En utilisant la notation que nous avons développée précédemment, l’estimation rapportée pour\(\mu_{rc}\), la moyenne pour le niveau r sur le facteur A (ligne) et le niveau c sur le facteur B (colonne) serait \(u_{\text{..}} + \alpha_{r} + \beta_{c}\). S’il n’y a vraiment aucune interaction entre les deux facteurs, il s’agit en fait d’une meilleure estimation de la moyenne de la population que la moyenne brute de l’échantillon. La suppression du terme d’interaction du modèle, via les options « Model » de l’analyse ANOVA de Jamovi, fournit les moyennes marginales pour l’analyse présentée à la Figure 14‑9.

Figure 14‑9 : capture d’écran de Jamovi montrant les moyennes marginales du modèle insaturé, c’est-à-dire sans la composante interaction, avec l’ensemble des données clinicaltrial

14.4 Vérification des hypothèses

Comme pour l’analyse de variance à un facteur, les hypothèses clés de l’analyse de variance factorielle sont l’homogénéité de la variance (tous les groupes ont le même écart-type), la normalité des résidus et l’indépendance des observations. Les deux premiers sont des choses qu’on peut vérifier. La troisième est quelque chose que vous devez évaluer vous-même en vous demandant s’il y a des relations spéciales entre les différentes observations, par exemple des mesures répétées où la variable indépendante est le temps, de sorte qu’il y a une relation entre les observations au temps un et au temps deux : les observations à différents moments proviennent des mêmes personnes. De plus, si vous n’utilisez pas un modèle saturé (par exemple, si vous avez omis les termes d’interaction), vous supposez également que les termes omis ne sont pas importants. Bien sûr, vous pouvez vérifier cette dernière en exécutant une ANOVA avec les termes omis inclus et voir s’ils sont significatifs, c’est assez donc facile. Qu’en est-il de l’homogénéité de la variance et de la normalité des résidus ? Il s’avère que c’est assez facile à vérifier. Ce n’est pas différent des contrôles que nous avons effectués pour une ANOVA à un facteur.

14.4.1 Homogénéité de la variance

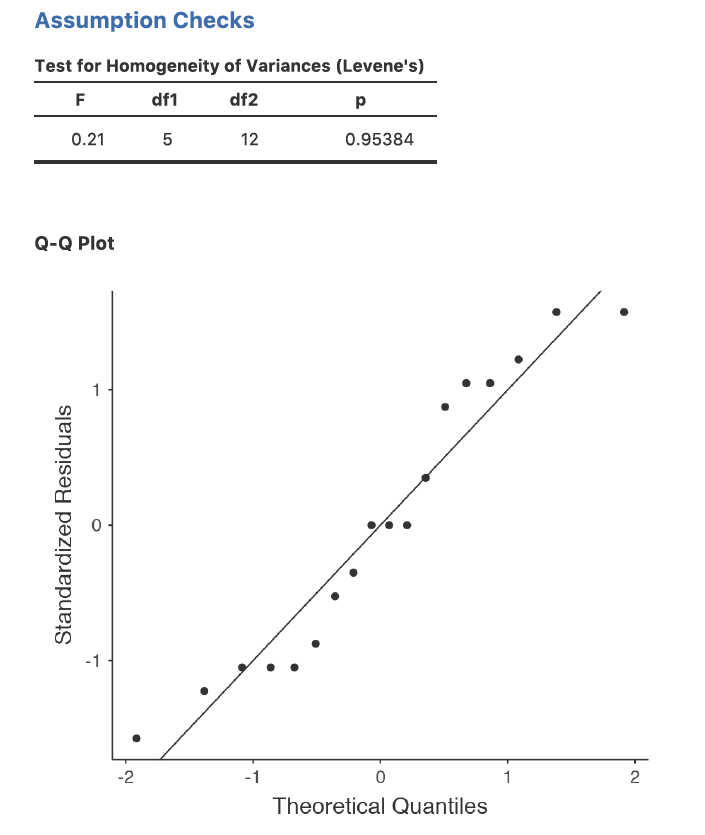
Comme nous l’avons mentionné à la section 13.6.1, il est bon d’inspecter visuellement un graphique des écarts-types comparés entre différents groupes ou catégories, et de voir si le test de Levene est conforme à l’inspection visuelle. La théorie qui sous-tend le test de Levene a été abordée à la section 13.6.1, de sorte que je n’en parlerai plus. Ce test s’attend à ce que vous ayez un modèle saturé (c.-à-d., incluant tous les éléments suivants les termes pertinents), parce que le test porte principalement sur la variance intra-groupe et qu’il n’est pas vraiment logique de calculer cela autrement que par rapport au modèle complet. Le test de Levene peut être spécifié dans le cadre de l’option de l’ANOVA « Assumption Checks » - « Homogeneity Tests » dans Jamovi, avec le résultat indiqué à la Figure 14‑10. Le fait que le test de Levene ne soit pas significatif signifie que, à condition qu’il soit cohérent avec une inspection visuelle du graphique des écarts-types, nous pouvons supposer avec certitude que l’hypothèse d’homogénéité de la variance n’est pas violée.

14.4.2 Normalité des résidus

Comme pour l’analyse de variance à sens unique, nous pouvons tester la normalité des résidus d’une manière simple et directe (voir la section 13.6.4). Cependant, c’est généralement une bonne idée d’examiner les résidus graphiquement à l’aide d’un graphe QQ. Voir la Figure 14‑10.

Figure 14‑10 : Vérification des présupposés dans un modèle d’ANOVA

14.5 Analyse de la covariance (ANCOVA)

Une variation de l’analyse de variance se produit lorsqu’il y a une variable continue supplémentaire qui, à votre avis, pourrait être liée à la variable dépendante. Cette variable supplémentaire peut être ajoutée à l’analyse en tant que covariable, dans l’analyse de covariance bien nommée (ANCOVA).

Dans ANCOVA, les valeurs de la variable dépendante sont « ajustées » pour tenir compte de l’influence de la covariable, puis les moyennes de score « ajustées » sont testées entre groupes de la manière habituelle. Cette technique peut augmenter la précision d’une expérience, et donc fournir un test plus « puissant » de l’égalité des moyennes de groupe pour la variable dépendante. Comment ANCOVA s’y prend-elle ? Bien que la covariable elle-même ne présente généralement aucun intérêt expérimental, l’ajustement pour la covariable peut diminuer l’estimation de l’erreur expérimentale et donc, en réduisant la variance de l’erreur, la précision est accrue. Cela signifie que rejeter l’hypothèse nulle de façon inappropriée (faux négatif ou erreur de type II) est moins probable.

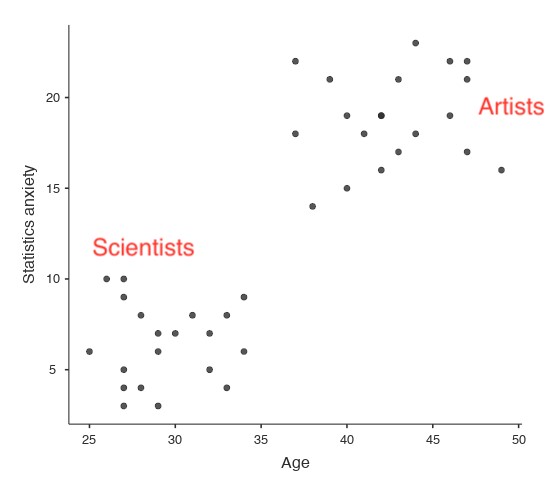
Malgré cet avantage, ANCOVA court le risque d’aplanir les différences réelles entre les groupes, ce qu’il faut éviter. Par exemple, regardez la Figure 14‑11, qui montre un graphique de l’aversion pour les statistiques par rapport à l’âge et dans deux groupes distincts - les élèves qui ont une formation ou une préférence en arts ou en sciences. ANCOVA avec l’âge comme covariable pourrait mener à la conclusion que l’anxiété statistique ne diffère pas entre les deux groupes. Cette conclusion serait-elle raisonnable - probablement pas parce que les âges des deux groupes ne se chevauchent pas et que l’analyse de la variance a essentiellement « extrapolé à une région sans données » (Everitt (1996), p. 68).

Figure 14‑11 : Représentation graphique de l’aversion aux statistiques par rapport à l’âge pour deux groupes distincts

De toute évidence, il faut réfléchir soigneusement à l’analyse de la covariance avec des groupes distincts. Ceci s’applique à la fois aux plans à un facteur et factorielles, car ANCOVA peut être utilisé avec les deux.

14.5.1 Exécuter ANCOVA en Jamovi

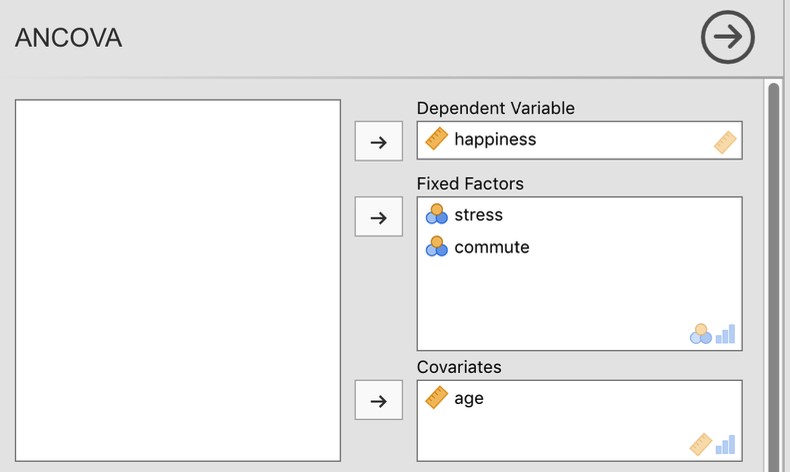
Un psychologue de la santé s’est intéressé à l’effet de l’utilisation habituelle du vélo et du stress sur les niveaux de bonheur, avec l’âge comme covariable. Vous pouvez trouver l’ensemble de données dans le fichier ancova.csv. Ouvrez ce fichier dans Jamovi et ensuite, pour entreprendre une ANCOVA, sélectionnez Analyses - ANOVA - ANCOVA pour ouvrir la fenêtre ANCOVA analysis (Figure 14‑12). Sélectionnez la variable dépendante « bonheur » et transférez-la dans la zone de texte « Dependant Variable ». Sélectionnez les variables indépendantes « stress » et « commute » et transférez-les dans la zone de texte « Fixed Factors ». Mettez en surbrillance la covariable « âge » et transférez-la dans la zone de texte « Covariables ». Cliquez ensuite sur Moyennes marginales estimées… pour afficher les options des graphiques et des tableaux.

Figure 14‑12 : La fenêtre d’analyse ANCOVA de Jamovi

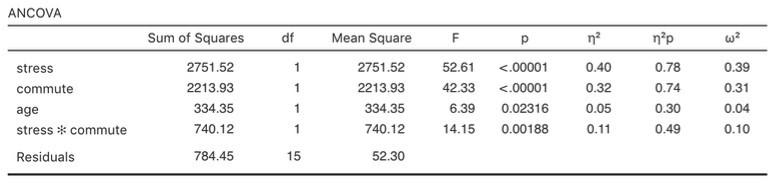
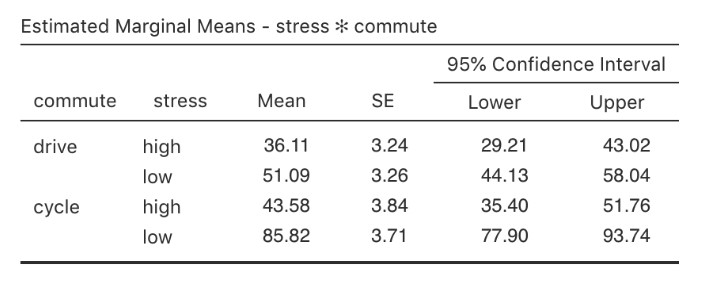
Un tableau ANCOVA montrant les tests sur les effets inter sujet est produit dans la fenêtre de résultats Jamovi (Figure 14‑13). La valeur F de la covariable « âge » est significative à p=.023, ce qui suggère que l’âge est un prédicteur important de la variable dépendante, le bonheur. Lorsque nous examinons les scores marginaux moyens estimés (Figure 14‑14), des ajustements ont été faits (par rapport à une analyse sans covariable) en raison de l’inclusion de la covariable « âge » dans cet ANCOVA. Un graphique (Figure 14‑15) est un bon moyen de visualiser et d’interpréter les effets significatifs.

La valeur F de l’effet principal « contrainte » (52,61) est associée à une probabilité de p<.001. La valeur F de l’effet principal « commute » (42,33) est associée à une probabilité de p<.001. Comme ces deux valeurs sont inférieures à la probabilité habituellement utilisée pour décider si un résultat statistique est significatif (p<.05), nous pouvons conclure qu’il y a eu un effet principal significatif du stress (F(1,15) = 52,61, p<.001) et un effet principal significatif de la méthode du transport quotidien (F(1,15) = 42,33, p<.001). Une interaction significative entre le stress et la mode de déplacement a également été trouvée (F(1,15) = 14,15, p=.002).

Figure 14‑13 : Résultats de l’ANCOVA dans Jamovi pour la variable bonheur (hapiness) en fonction du stress et du mode de déplacement (commute), avec l’âge comme covariable.

Figure 14‑14 : Tableau du niveau de bonheur moyen en fonction du stress et de la mode de déplacement (ajusté pour l’âge covarié) avec des intervalles de confiance à 95 %.

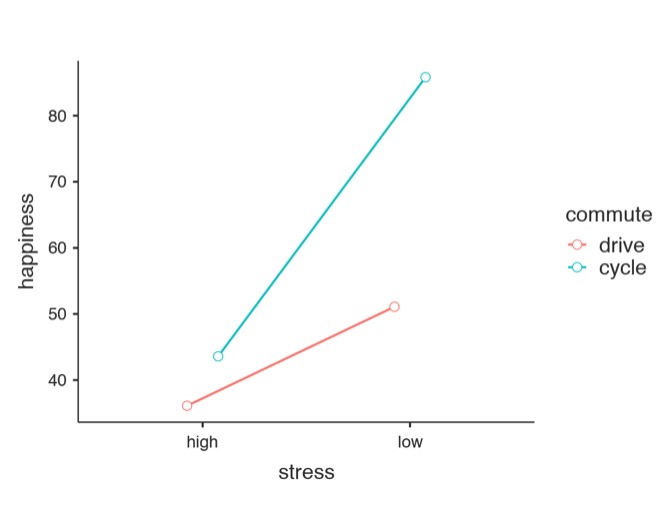
Dans la Figure 14‑15, nous pouvons voir les scores de bonheur ajustés, marginaux et moyens lorsque l’âge est une covariable dans une ANCOVA. Dans cette analyse, il existe un effet d’interaction significatif, selon lequel les personnes peu stressées qui se rendent au travail à vélo sont plus heureuses que les personnes peu stressées qui y vont en voiture et les personnes très stressées, qu’elles se rendent au travail à vélo ou en voiture. Il y a aussi un effet principal important du stress - les personnes peu stressées sont plus heureuses que celles qui sont très stressées. Et il y a aussi un effet principal important du comportement de déplacement domicile-travail - les gens qui font du vélo sont en moyenne plus heureux que ceux qui se rendent au travail en voiture.

Figure 14‑15 : Diagramme du niveau de bonheur moyen en fonction du stress et de la méthode de déplacement

Vous devez être attentif au fait que, si vous songez à inclure une covariable dans votre analyse de variance, il y a une hypothèse supplémentaire : la relation entre la covariable et la variable dépendante doit être semblable pour tous les niveaux de la variable indépendante. Ceci peut être vérifié par l’ajout d’un terme d’interaction entre la covariable et chaque variable indépendante dans les options de Jamovi « Model - Model terms ». Si l’effet d’interaction n’est pas significatif, il peut être supprimé. S’il est significatif, alors une technique statistique différente et plus avancée pourrait être appropriée (ce qui dépasse le cadre de ce livre et vous voudrez peut-être consulter un statisticien amical).

14.6 ANOVA comme modèle linéaire

L’une des choses les plus importantes à comprendre au sujet de l’analyse de variance et de la régression est qu’il s’agit essentiellement de la même chose. À première vue, on ne le croirait peut-être pas. Après tout, la façon dont je les ai décrites jusqu’à présent suggère que l’analyse de variance vise principalement à vérifier les différences entre les groupes et que la régression vise principalement à comprendre les corrélations entre les variables. Et, pour autant que je sache, c’est tout à fait vrai. Mais quand on regarde dans le moteur, pour ainsi dire, les mécanismes sous-jacents de l’analyse de variance et de la régression sont terriblement semblables. En fait, si vous y pensez, vous en avez déjà vu la preuve. L’analyse de variance et la régression reposent toutes deux fortement sur des sommes de carrés (SS), toutes deux font appel à des tests F, et ainsi de suite. Rétrospectivement, il est difficile d’échapper au sentiment que les chapitres 12 et 13 étaient un peu répétitifs.

La raison en est que l’analyse de variance et la régression sont deux types de modèles linéaires. Dans le cas de la régression, c’est un peu évident. L’équation de régression que nous utilisons pour définir la relation entre les prédicteurs et les résultats est l’équation d’une droite, donc c’est de toute évidence un modèle linéaire, avec l’équation suivante

\[ Y_{p} = b_{0} + b_{1}X_{1p} + b_{2}X_{2p} + \epsilon_{p} \]

où Y_p est la valeur finale de la p-ième observation (c.-à-d., p-ième personne), X_1p est la valeur du premier prédicteur de la p-ième observation, X_2p est la valeur du deuxième prédicteur de la p-ième observation, les termes b₀, b₁ et b₂ sont nos coefficients de régression, et \(\epsilon_{p}\) est le p-ième résidu. Si nous ignorons les résidus \(\epsilon_{p}\) et que nous nous concentrons sur la ligne de régression elle-même, nous obtenons la formule suivante :

\[ {\hat{Y}}_{p} = b_{0} + b_{1}X_{1p} + b_{2}X_{2p} \]

où \({\hat{Y}}_{p}\) est la valeur de Y que la ligne de régression prédit pour la personne p, par opposition à la valeur Y_p réellement observée. Ce qui n’est pas immédiatement évident, c’est que nous pouvons aussi écrire ANOVA comme modèle linéaire. C’est en fait assez simple à faire. Commençons par un exemple très simple, en réécrivant une ANOVA factorielle 2 x 2 comme modèle linéaire.

14.6.1 Quelques données

Pour concrétiser les choses, supposons que notre variable de résultat est la grade (note) qu’un élève reçoit dans mon cours, une variable sur une échelle de rapport correspondant à une note de 0% à 100%. Il y a deux variables prédictrices d’intérêt : si l’étudiant s’est présenté aux cours (la variable attend (fréquentation)) et si l’étudiant a lu ou non le manuel (la variable reading (lecture)). Nous dirons que attend=1 si l’élève a assisté au cours, et de 0 s’il n’y a pas assisté. De même, nous dirons que reading = 1 si l’élève a lu le manuel, et reading = 0 s’il ne l’a pas lu.

Bien, pour l’instant c’est assez simple. La prochaine chose que nous devons faire est d’enrober cela d’un peu de maths (désolé !). Pour les besoins de cet exemple, supposons que Y_p indique la note du cinquième élève de la classe. Ce n’est pas tout à fait la même notation que celle que nous avons utilisée plus tôt dans ce chapitre. Auparavant, nous avons utilisé la notation Y_rci pour désigner la i-ème personne du r-ème groupe pour le prédicteur 1 (le facteur de ligne) et le c-ème groupe pour le prédicteur 2 (le facteur de colonne). Cette notation générale était vraiment pratique pour décrire le calcul des SS, mais c’est une souffrance dans le contexte actuel, alors je vais changer de notation ici. Maintenant, la notation Y_p est visuellement plus simple que Y_rci, mais elle a le défaut de ne pas garder la trace des membres du groupe ! C’est-à-dire, si je vous disais que Y_0,0,3=35, vous sauriez immédiatement qu’il s’agit d’un étudiant (le 3e de ce type, en fait) qui n’a pas assisté aux cours (c.-à-d., attend=0) et n’a pas lu le manuel (c.-à-d., reading=0), et qui a échoué en cours (Grade=35). Mais si je vous dis que Y_p=35, tout ce que vous savez, c’est que le p-ième étudiant n’a pas eu une bonne note. Nous avons perdu des informations clés. Bien sûr, il ne faut pas beaucoup de réflexion pour comprendre comment régler ce problème. Ce que nous allons faire à la place est d’introduire deux nouvelles variables X_1p et X_2p qui gardent la trace de ces informations. Dans le cas de notre étudiant hypothétique, nous savons que X_1p=0 (c.-à-d., attend = 0) et X_2p=0 (c.-à-d., reading=0). Les données pourraient donc ressembler à ceci :

personne, p	grade, Yp	attendance, *X~1p	~* | lecture, X2p
1	90	1	1
2	87	1	1
3	75	0	1
4	60	1	0
5	35	0	0
6	50	0	0
7	65	1	0
8	70	0	1

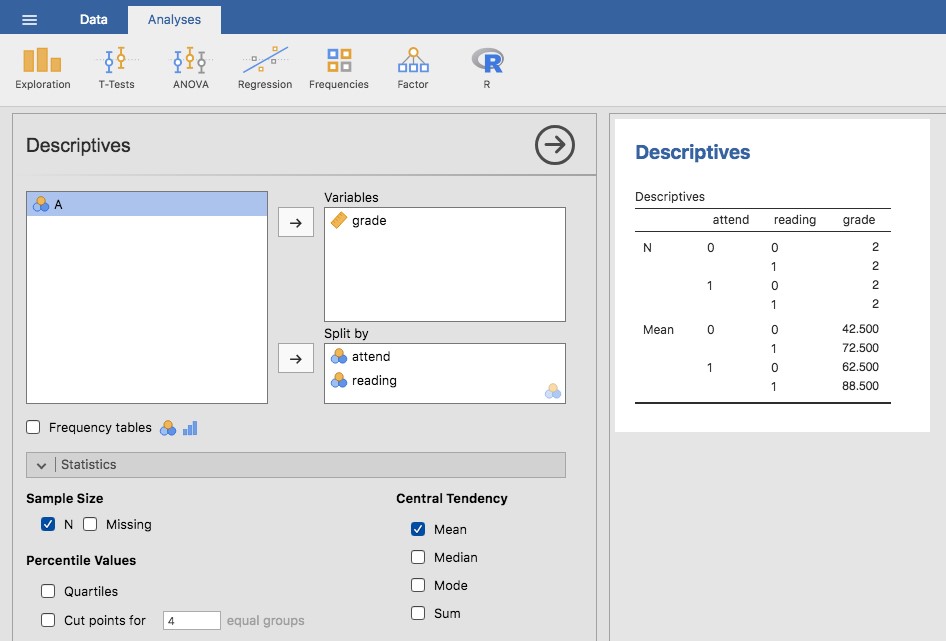
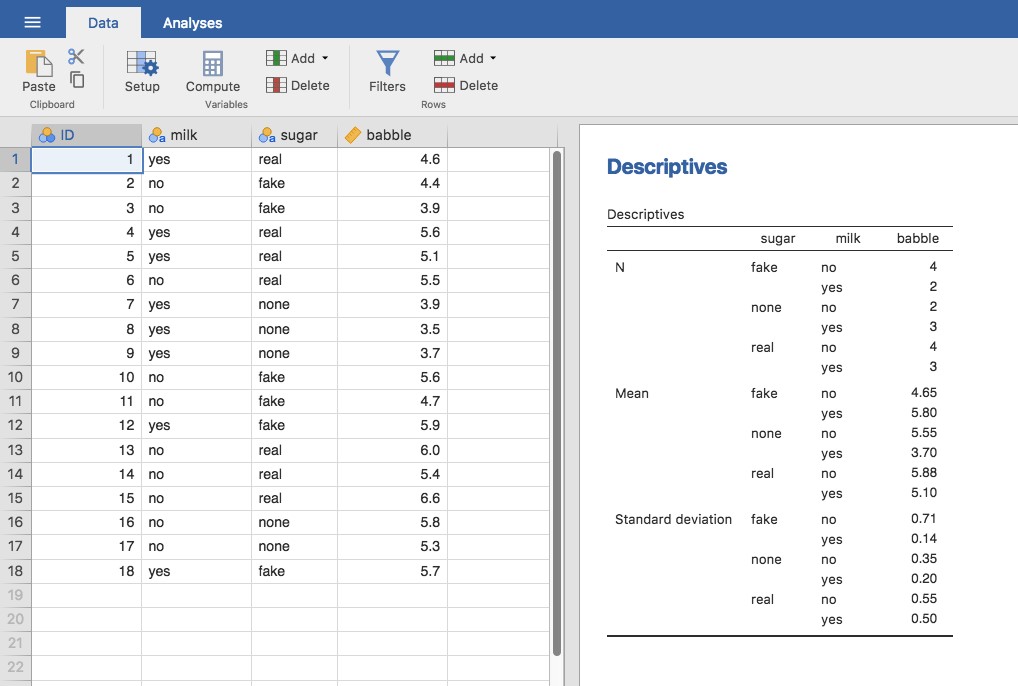
Il n’y a rien de particulier, bien sûr. C’est exactement le format dans lequel nous nous attendons à voir nos données ! Voir le fichier rtfm.csv. Nous pouvons utiliser l’analyse « Descriptives » de Jamovi pour confirmer que cet ensemble de données correspond à un plan équilibré, avec 2 observations pour chaque combinaison de attend et de read. De la même manière, nous pouvons également calculer la note moyenne pour chaque combinaison. C’est ce que montre la Figure 14‑16. En regardant les notes moyennes, on a la forte impression que la lecture du texte et le fait d’assister aux cours sont très importants.

Figure 14‑16: Statistiques descriptives dans Jamovi pour l’ensemble de données rtfm.csv

14.6.2 ANOVA avec des facteurs binaires comme modèle de régression

Bien, revenons aux mathématiques. Nous avons maintenant nos données exprimées avec trois variables numériques : la variable continue Y et les deux variables binaires X₁ et X₂. Ce que je veux que vous reconnaissiez, c’est que notre ANOVA factorielle 2x2 est strictement équivalente au modèle de régression.

\[ Y_{p} = b_{0} + b_{1}X_{1p} + b_{2}X_{2p} + \epsilon_{p} \]

Bien sûr, c’est exactement la même équation que celle que j’ai utilisée plus tôt pour décrire un modèle de régression à deux prédicteurs ! La seule différence est que X₁ et X₂ sont maintenant des variables binaires (c.-à-d. que les valeurs ne peuvent être que 0 ou 1), alors que dans une analyse de régression, nous prévoyons que X₁ et X₂ seront continues. Il y a deux ou trois façons dont je pourrais essayer de vous en convaincre. Une possibilité serait de faire un long exercice mathématique pour prouver que les deux sont identiques. Cependant, je vais anticiper et deviner que la plupart des lecteurs de ce livre trouveront cela ennuyeux plutôt qu’utile. Au lieu de cela, j’expliquerai les idées de base et je m’appuierai sur Jamovi pour montrer que les analyses ANOVA et les analyses de régression ne sont pas seulement similaires, elles sont identiques. Commençons par faire une analyse de variance. Pour ce faire, nous utiliserons l’ensemble de données rtfm.csv, et regardons la Figure 14‑17 qui montre ce qu’on obtient quand on fait l’analyse à Jamovi.

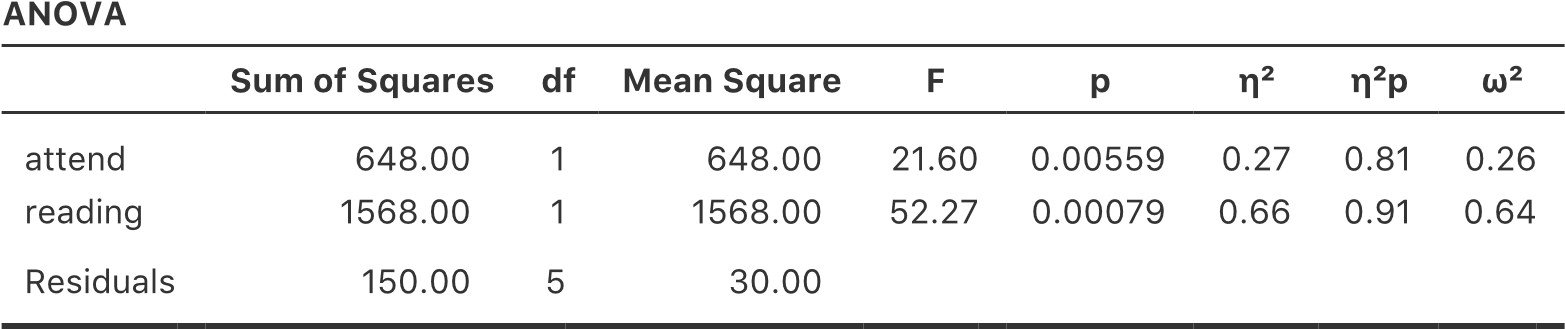
Figure 14‑17 : ANOVA de l’ensemble de données rtfm.csv dans Jamovi, sans le terme d’interaction

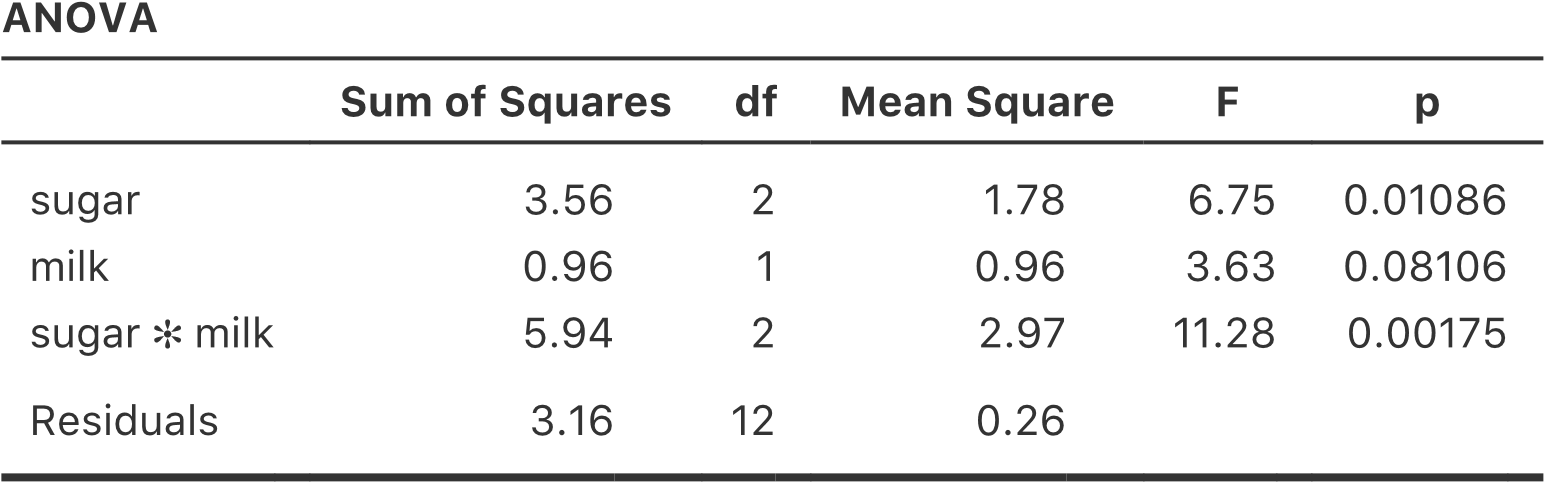
En lisant les chiffres clés du tableau de l’ANOVA et les scores moyens que nous avons présentés plus haut, nous pouvons voir que les élèves ont obtenu une meilleure note s’ils ont suivi la classe (F(1,5)=21,6, p=.0056) et s’ils lisent le manuel (F(1,5)=52.3, p=.0008). Notons ces valeurs p et ces statistiques F.

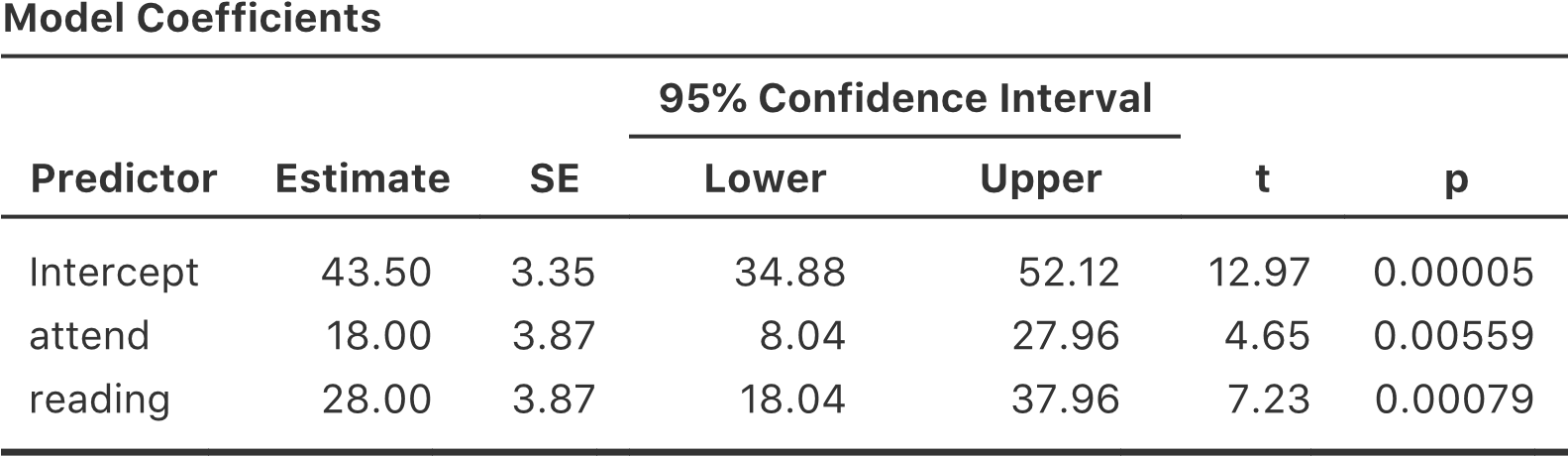
Pensons maintenant à la même analyse dans une perspective de régression linéaire. Dans l’ensemble de données rtfm.csv, nous avons encodé attend et la read comme s’il s’agissait de prédicteurs numériques. Dans ce cas, c’est tout à fait acceptable. Il y a vraiment un sens au fait qu’un étudiant qui se présente en classe (c.-à-d. attend = 1) a en fait « plus de présence » qu’un étudiant qui ne le fait pas (c.-à-d. attend = 0). Il n’est donc pas du tout déraisonnable de l’inclure comme prédicteur dans un modèle de régression. C’est un peu inhabituel, car le prédicteur ne prend que deux valeurs possibles, mais il ne viole aucune des hypothèses de la régression linéaire. Et c’est facile à interpréter. Si le coefficient de régression est supérieur à 0, cela signifie que les étudiants qui assistent à des cours ont des notes plus élevées. Si elle est inférieure à zéro, les étudiants qui assistent à des cours magistraux obtiennent des notes moins élevées. Il en va de même pour notre variable de read.

Attendez une seconde. Pourquoi est-ce vrai ? C’est quelque chose qui est intuitivement évident pour tous ceux qui ont suivi quelques cours de statistiques et qui sont à l’aise avec les mathématiques, mais ce n’est pas clair pour tout le monde au premier abord. Pour comprendre pourquoi c’est vrai, il est utile d’examiner de près quelques élèves en particulier. Commençons par considérer les 6e et 7e élèves de notre ensemble de données (c.-à-d. p = 6 et p = 7). Ni l’un ni l’autre n’a lu le manuel, de sorte que dans les deux cas, nous pouvons fixer read à 0, ou, pour dire la même chose dans notre notation mathématique, nous observons X_2,6=0 et X_2,7=0, mais l’étudiant numéro 7 est venu aux cours (c’est à dire attend = 1, X_1,7=1) tandis que l’étudiant numéro 6 ne l’est pas (c’est-à-dire attend=0, *X_1,6=0). Voyons maintenant ce qui se passe lorsque nous insérons ces nombres dans la formule générale de notre ligne de régression. Pour l’élève numéro 6, la régression prédit que

\[\begin{aligned} \hat{Y}_{6} &= b_{0} + b_{1}X_{1,6} + b_{2}X_{2,6}\\ &= b_{0}+\left( b_{1} \times 0 \right) + \left( b_{2} \times 0 \right)\\ &= b_{0} \end{aligned} \]

On s’attend donc à ce que cet élève obtienne une note correspondant à la valeur du terme d’intersection b₀. Et l’élève 7 ? Cette fois, lorsque nous insérons les nombres dans la formule de la ligne de régression, nous obtenons ce qui suit

\[\begin{aligned} \hat{Y}_{7} &= b_{0} + b_{1}X_{1,7} + b_{2}X_{2,7}\\ &= b_{0}+\left( b_{1} \times 1 \right) + \left( b_{2} \times 0 \right)\\ &= b_{0} + b_{1} \end{aligned} \]

Étant donné que cet élève a fréquenté la classe, la note prévue est égale au terme d’intersection b₀ plus le coefficient associé à la variable attend, b₁. Donc, si b₁ est supérieur à zéro, nous nous attendons à ce que les étudiants qui se présentent aux cours magistraux obtiennent de meilleures notes que ceux qui ne le font pas. Si ce coefficient est négatif, on s’attend à l’inverse : les élèves qui se présentent en classe obtiennent de bien pires résultats. En fait, nous pouvons aller un peu plus loin. Qu’en est-il de l’élève numéro 1, qui s’est présenté en classe (X_1,1=1) et a lu le manuel (X_2,1=1) ? Si nous connectons ces chiffres à la régression, nous obtenons

\[\begin{aligned} \hat{Y}_{1} &= b_{0} + b_{1}X_{1,1} + b_{2}X_{2,2}\\ &= b_{0}+\left( b_{1} \times 1 \right) + \left( b_{2} \times 1 \right)\\ &= b_{0} + b_{1} + b_{2} \end{aligned} \]

Donc, si nous supposons que le fait d’aller en classe vous aide à obtenir une bonne note (c.-à-d. b₁>0) et si nous supposons que la lecture du manuel vous aide également à obtenir une bonne note (c.-à-d. b2 > 0), nous nous attendons à ce que l’élève 1 obtienne une note supérieure à celle des élèves 6 et 7.

Et à ce stade, vous ne serez pas du tout surpris d’apprendre que le modèle de régression prédit que l’étudiant 3, qui a lu le livre mais n’a pas assisté aux cours, obtiendra une note b₂>b₀. Je ne vous ennuierai pas avec une autre formule de régression. Je vais plutôt vous montrer le tableau suivant des notes attendues :

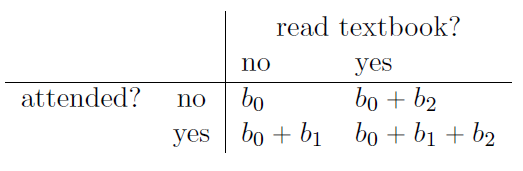
Comme vous pouvez le constater, le terme d’interception b₀ agit comme une sorte de note de base à laquelle on s’attendrait de la part des élèves qui ne prennent pas le temps d’aller en classe ou de lire le manuel scolaire. De même, b₁ représente l’augmentation que l’on s’attend à recevoir si vous venez en classe, et b₂ représente l’augmentation qui vient de la lecture du manuel scolaire. En fait, s’il s’agissait d’une ANOVA, vous pourriez très bien vouloir caractériser b₁ comme l’effet principal de la fréquentation, et b₂ comme l’effet principal de la lecture ! En fait, pour un simple 2 x 2 ANOVA, c’est exactement comme ça que ça se passe.

Ok, maintenant que nous commençons vraiment à voir pourquoi ANOVA et la régression sont fondamentalement la même chose, exécutons notre régression en utilisant les données rtfm.csv et l’analyse de régression de Jamovi pour nous convaincre que cela est vraiment vrai. L’exécution de la régression de la manière habituelle donne les résultats présentés à la Figure 14‑18.

Figure 14‑18 : Analyse de régression de l’ensemble de donnéesrtfm.csv dans Jamovi, sans le terme d’interaction

Il y a quelques choses intéressantes à noter ici. Notons d’abord que le terme d’intersection est 43,5, ce qui est proche de la moyenne de 42,5 observée pour les deux élèves qui n’ont pas lu le texte ou qui n’ont pas assisté aux cours. Deuxièmement, nous avons le coefficient de régression b₁=18,0 pour la variable attend, ce qui suggère que les élèves qui ont assisté aux cours ont obtenu 18 % de plus que ceux qui ne l’ont pas fait. Nous nous attendions donc à ce que les élèves qui se présentaient en classe mais qui ne lisaient pas le manuel obtiennent une note de b₀ + b₁, ce qui est égal à 43,5 + 18,0 = 61,5. Vous pouvez vérifier par vous-même que la même chose se produit lorsque nous regardons les élèves qui lisent le manuel.

En fait, nous pouvons aller un peu plus loin dans l’établissement de l’équivalence de notre analyse de variance et de notre régression. Examinez les valeurs p associées à la variable attend et à la variable read dans la sortie de régression. Elles sont identiques à celles que nous avons rencontrées plus tôt lors de l’exécution de l’ANOVA. Cela peut paraître un peu surprenant, puisque le test utilisé lors de l’exécution de notre modèle de régression calcule une statistique t et que l’ANOVA calcule une statistique F. Cependant, si vous vous rappelez tout au long du chapitre 7, j’ai mentionné qu’il y a une relation entre la distribution t et la distribution F. Si vous avez une certaine quantité qui est distribuée selon une distribution t avec k degrés de liberté et que vous l’élevez au carré, alors cette nouvelle quantité au carré suit une distribution F dont les degrés de liberté sont 1 et k. Nous pouvons vérifier ceci par rapport aux statistiques t dans notre modèle de régression. Pour la variable attend, nous obtenons une valeur t de 4,65. Si nous élevons au carré ce nombre, nous obtenons 21,6, ce qui correspond à la statistique F correspondante dans notre analyse de variance.

Enfin, une dernière chose que vous devriez savoir. Parce que Jamovi intègre le fait que ANOVA et la régression sont deux exemples de modèles linéaires, il vous permet d’extraire la table ANOVA classique de votre modèle de régression en utilisant la « Linear Regression » - « Model Coefficients » - « Omnibus Test » - « ANOVA Test », et ceci vous donnera le tableau présenté dans la Figure 14‑19.

Figure 14‑19 : Résultats du test Omnibus ANOVA de l’analyse de régression de Jamovi

14.6.3 Comment coder les facteurs non binaires en tant que contrastes

A ce stade, je vous ai montré comment nous pouvons visualiser un 2x2 ANOVA dans un modèle linéaire. Et il est assez facile de voir comment cela se généralise à une ANOVA 2 x 2 x 2 x 2 ou ANOVA une 2 x 2 x 2 x 2 x 2. C’est la même chose, vraiment. Vous ajoutez simplement une nouvelle variable binaire pour chacun de vos facteurs. Ce qui commence à se compliquer, c’est quand on considère les facteurs qui ont plus de deux niveaux. Prenons, par exemple, l’analyse de variance 3 x 2 que nous avons effectuée plus tôt dans ce chapitre à l’aide des données de clinicaltrial.csv. Comment pouvons-nous convertir le facteur médicament à trois niveaux en une forme numérique qui convient à une régression ?

La réponse à cette question est assez simple, en fait. Tout ce que nous avons à faire est de réaliser qu’un facteur à trois niveaux peut être réécrit comme deux variables binaires. Supposons, par exemple, que je crée une nouvelle variable binaire appelée druganxifree. Chaque fois que la variable drug est égale à « anxifree » on met druganxifree = 1. Cette variable établit un contraste, dans ce cas-ci entre anxifree et les deux autres médicaments. En soi, bien sûr, le contraste druganxifree n’est pas suffisant pour saisir toute l’information de notre variable drug. Nous avons besoin d’un deuxième contraste, un contraste qui nous permette de distinguer le joyzepam du placebo. Pour ce faire, nous pouvons créer un second contraste binaire, appelé drugjoyzepam, qui est égal à 1 si le médicament est le joyzepam et à 0 s’il ne l’est pas. Ensemble, ces deux contrastes nous permettent d’établir une distinction parfaite entre les trois drogues possibles. Le tableau ci-dessous l’illustre bien :

Si le médicament administré à un patient est un placebo, les deux variables de contraste seront égales à 0 ; si le médicament est Anxifree, la variable druganxifree sera égale à 1, et drugjoyzepam sera égal à 0 ; l’inverse est vrai pour Joyzepam : drugjoyzepam est égal à 1 et druganxifree est égal à 0.

Créer des variables de contraste n’est pas trop difficile à faire à l’aide de la commande de calcul de nouvelles variables de Jamovi. Par exemple, pour créer la variable druganxifree, écrivez cette expression logique dans la boîte de calcul de la nouvelle variable : IF(drug ==‘anxifree’, 1, 0)‘. De même, pour créer la nouvelle variable drugjoyzepam utiliser cette expression logique : IF(drug ==’joyzepam’, 1, 0). Il en va de même pour la CBT Therapy : IF(therapy ==‘CBT’, 1, 0). Vous pouvez voir ces nouvelles variables, et les expressions logiques correspondantes, dans le fichier de données Jamovi clinicaltrial2.omv.

Nous avons maintenant recodé notre facteur à trois niveaux en termes de deux variables binaires, et nous avons déjà vu que l’ANOVA et la régression se comportent de la même manière pour les variables binaires. Toutefois, d’autres complexités surgissent dans ce cas, dont nous parlerons dans la section suivante.

14.6.4 L’équivalence entre ANOVA et régression pour les facteurs non binaires

Nous avons maintenant deux versions différentes du même ensemble de données. Nos données originales dans lesquelles la variable drug du fichier clinicaltrial.csv est exprimée comme un seul facteur à trois niveaux, et les données étendues clinicaltrial2.omv dans lesquelles elle est développée en deux contrastes binaires. Encore une fois, ce que nous voulons démontrer, c’est que notre ANOVA factorielle originale de 3 x 2 est équivalente à un modèle de régression appliqué aux variables de contraste. Commençons par relancer l’analyse de variance, dont les résultats sont présentés à la Figure 14‑20.

Figure 14‑20 : résultats de l’analyse de variance de Jamovi, sans composante d’interaction

Évidemment, il n’y a pas de surprise ici. C’est exactement la même analyse de variance que celle qu’on a faite tout à l’heure. Ensuite, effectuons une régression en utilisant comme prédicteurs le druganxifree, le drugjoyzepam et la CBTtherapy. Les résultats sont présentés à la Figure 14‑21.

Figure 14‑21 : résultats de la régression de Jamovi, avec variables de contraste druganxifree et drugjoyzepam

Ouais. Ce n’est pas le même résultat que la dernière fois. Comme on pouvait s’y attendre, la sortie de régression donne les résultats de chacun des trois prédicteurs séparément, tout comme elle l’a fait chaque fois que nous avons effectué une analyse de régression. D’une part, nous pouvons voir que la valeur p de la variable CBTtherapy est exactement la même que celle du facteur therapy dans notre analyse de variance originale, de sorte que nous pouvons être rassurés que le modèle de régression fait la même chose que l’analyse de variance. D’autre part, ce modèle de régression teste séparément le contraste du médicament sansanxiforme et le contraste du médicament joyzepam, comme s’il s’agissait de deux variables complètement différentes. Ce n’est pas surprenant, bien sûr, parce que l’analyse de régression médiocre n’a aucun moyen de savoir que le drugjoyzepam et le druganxifree sont en fait les deux contrastes différents que nous utilisons pour coder notre facteur drug à trois niveaux. Pour autant qu’elle le sache, le drugjoyzepam et le druganxifree ne sont pas plus apparentés que le drugjoyzepam et la therapyCBT. Cependant, nous savons que c’est mieux. À ce stade, nous ne sommes pas du tout intéressés à déterminer si ces deux contrastes sont significatifs individuellement. Nous voulons juste savoir s’il y a un effet « global » du médicament. C’est-à-dire, ce que nous voulons que Jamovi fasse, c’est de faire une sorte de test de « comparaison de modèles », un test dans lequel les deux contrastes « liés au médicament » sont mis dans le même panier pour les besoins du test. Ça vous dit quelque chose ? Tout ce que nous avons à faire est de spécifier notre modèle d’hypothèse nulle, qui dans ce cas inclurait le prédicteur de la CBTherapy, et d’omettre les deux variables liées au médicament, comme dans la Figure 14‑22.

Bien, c’est mieux comme ça. Notre statistique F est de 26,15, les degrés de liberté sont 2 et 14, et la valeur p est 0,0000002. Les chiffres sont identiques à ceux que nous avons obtenus pour l’effet principal du facteur drug dans notre analyse de variance originale. Encore une fois, nous constatons que l’analyse de variance et la régression sont fondamentalement les identiques. Il s’agit de deux modèles linéaires, et le mécanisme statistique sous-jacent de l’analyse de variance est identique à celui utilisé pour la régression. L’importance de ce fait ne doit pas être sous-estimée. Tout au long de ce chapitre, nous allons nous appuyer fortement sur cette idée.

Bien que nous ayons passé en revue tous les défauts du calcul de nouvelles variables dans Jamovi pour les contrastes druganxifree et drugjoyzepam, juste pour montrer que l’ANOVA et la régression sont fondamentalement les mêmes, dans l’analyse de régression linéaire de Jamovi il existe en fait un raccourci pratique pour obtenir ceux-ci. voir Figure 14‑23.

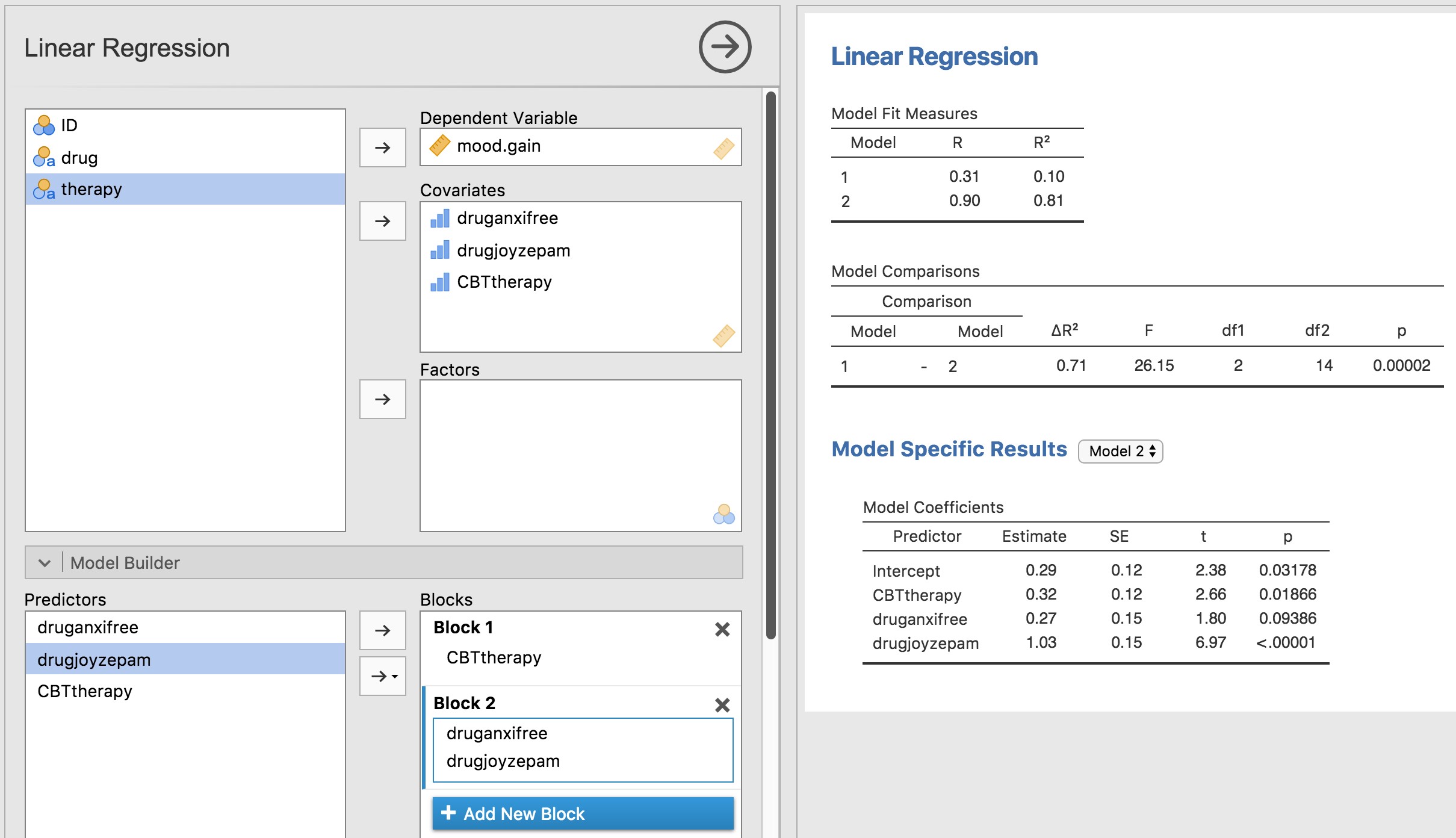
Figure 14‑22 : Comparaison des modèles de régression dans Jamovi, modèle d’hypothèse nul 1 vs modèle de contraste 2

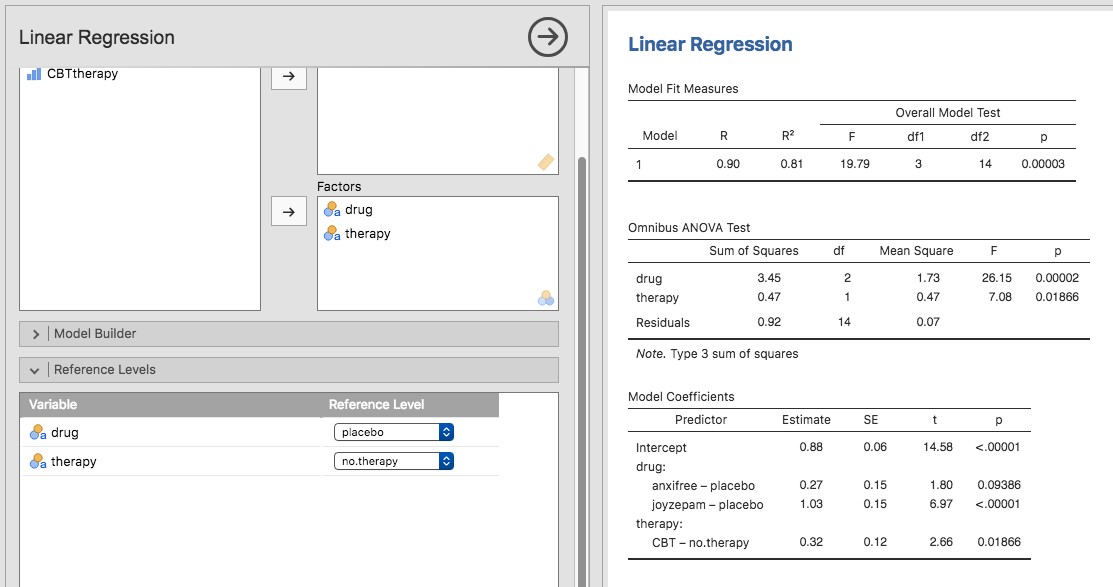
Figure 14‑23 : Analyse de régression avec facteurs et contrastes dans Jamovi, y compris omnibus

Ce que Jamovi fait ici, c’est vous permettre d’entrer les variables prédictrices comme des facteurs, attendez, comme des …facteurs ! Intelligent, non. Vous pouvez également spécifier le groupe à utiliser comme niveau de référence, via l’option « Reference Levels ». Nous l’avons changé pour « placebo » et « no.therapy », respectivement, parce que c’est le plus logique.

Si vous cliquez également sur la case à cocher ‘ANOVA’ sous l’option ‘Model Coefficients’ -‘Omnibus Test’, nous voyons que la statistique F est 26,15, les degrés de liberté sont 2 et 14, et la valeur p est 0,00002 (Figure 14‑23). Les chiffres sont identiques à ceux que nous avons obtenus pour l’effet principal de drug dans notre analyse de variance originale. Encore une fois, nous constatons que l’analyse de variance et la régression sont fondamentalement les mêmes. Il s’agit de deux modèles linéaires, et le mécanisme statistique sous-jacent de l’analyse de variance est identique à celui utilisé pour la régression.

14.6.5 Degrés de liberté comme comptage de paramètres !

Enfin, je peux enfin donner une définition des degrés de liberté dont je suis satisfait. Les degrés de liberté sont définis en fonction du nombre de paramètres qui doivent être estimés dans un modèle. Pour un modèle de régression ou une analyse de variance, le nombre de paramètres correspond au nombre de coefficients de régression (c.-à-d. les valeurs b), y compris l’intersection. En gardant à l’esprit que tout test F est toujours une comparaison entre deux modèles et le premier df est la différence du nombre de paramètres. Par exemple, dans la comparaison de modèles ci-dessus, le modèle nul (mood.gain ~ therapyCBT) a deux paramètres : il y a un coefficient de régression pour la variable therapyCBT, et un autre pour l’interception. Le modèle alternatif (mood.gain ~ druganxifree + drugjoyzepam + therapyCBT) a quatre paramètres : un coefficient de régression pour chacun des trois contrastes, et un autre pour l’interception. Le degré de liberté associé à la différence entre ces deux modèles est donc df₁=4-2=2.

Qu’en est-il du cas où il ne semble pas y avoir de modèle d’hypothèse nulle ? Par exemple, vous pouvez penser au test F qui apparaît lorsque vous sélectionnez « Test F » dans les options « Linear Regression » - « Model Fit ». J’ai d’abord décrit cela comme un test du modèle de régression dans son ensemble. Toutefois, il s’agit toujours d’une comparaison entre deux modèles. Le modèle de l’hypothèse nulle est le modèle trivial qui ne comprend qu’un seul coefficient de régression, pour le terme d’intersection. Le modèle alternatif contient K+1 coefficients de régression, un pour chacune des K variables prédicteurs et un autre pour l’interception. Donc la valeur df que vous voyez dans ce test F est égale à df1=K+1-1=K.

Qu’en est-il de la deuxième valeur df qui apparaît dans le test F ? Il s’agit toujours des degrés de liberté associés aux résidus. Il est également possible d’envisager cela en termes de paramètres, mais d’une manière légèrement contre-intuitive. Pensez-y comme ça. Supposons que le nombre total d’observations dans l’ensemble de l’étude est N. Si vous voulez décrire parfaitement chacune de ces N valeurs, vous devez le faire en utilisant, eh bien…. N nombres. Lorsque vous construisez un modèle de régression, ce que vous faites en réalité, c’est de spécifier que certains des nombres doivent parfaitement décrire les données. Si votre modèle a K prédicteurs et une intersection, alors vous avez spécifié K + 1 nombres. Donc, sans prendre la peine de déterminer exactement comment cela serait fait, combien d’autres chiffres faudra-t-il, selon vous, pour transformer un modèle de régression de paramètres K+1 en une description parfaite des données brutes ? Si vous pensez (K+1)+(N-K-1q)=N, et donc que la réponse devrait être N–K-1, vous avez gagné ! C’est exactement ça. En principe, vous pouvez imaginer un modèle de régression d’une complexité absurde qui inclut un paramètre pour chaque point de données unique, et qui fournirait bien sûr une description parfaite des données. Ce modèle contiendrait N paramètres au total, mais nous nous intéressons à la différence entre le nombre de paramètres requis pour décrire ce modèle complet (c.-à-d. N) et le nombre de paramètres utilisés par le modèle de régression plus simple qui vous intéresse réellement (c.-à-d. K+1), et donc le deuxième degré de liberté du test F est df₂ = N-K-1, où K est le nombre de variables explicatives (dans un modèle de régression) ou le nombre de contrastes (dans une ANOVA). Dans l’exemple que j’ai donné ci-dessus, il y a N=18 observations dans l’ensemble de données et K+1=4 coefficients de régression associés au modèle ANOVA, donc les degrés de liberté des résidus sont df₂=18-4=14.

14.7 Différentes façons de spécifier les contrastes

Dans la section précédente, je vous ai montré une méthode pour convertir un facteur en une collection de contrastes. Dans la méthode que je vous ai montrée, nous spécifions un ensemble de variables binaires dans lequel nous avons défini une table comme celle-ci :

Chaque ligne du tableau correspond à l’un des niveaux de facteurs et chaque colonne correspond à l’un des contrastes. Cette table, qui a toujours une ligne de plus que les colonnes, a un nom spécial. C’est ce qu’on appelle une matrice de contrastes. Cependant, il existe de nombreuses façons de spécifier une matrice de contrastes. Dans cette section, j’aborde quelques-unes des matrices de contrastes standard utilisées par les statisticiens et la façon dont vous pouvez les utiliser dans les Jamovi. Si vous avez l’intention de lire la section sur l’ANOVA non équilibrée plus loin (Section 14.10), cela vaut la peine de lire attentivement cette section. Si ce n’est pas le cas, vous pouvez vous contenter de la survoler, car le choix des contrastes n’a pas beaucoup d’importance pour des motifs équilibrés.

14.7.1 Les contrastes de traitement

Dans le type particulier de contrastes que j’ai décrit ci-dessus, un niveau du facteur est spécial et agit comme une sorte de catégorie de « référence » (c.-à-d. placebo dans notre exemple), par rapport à laquelle les deux autres sont définis. Le nom de ce type de contrastes est celui de contraste de traitement, également connus sous le nom de « faux codage ». Dans ce contraste, chaque niveau du facteur est comparé à un niveau de référence de base, et le niveau de référence de base est la valeur de l’interception.

Le nom reflète le fait que ces contrastes sont tout à fait naturels et raisonnables quand l’une des catégories de votre facteur est vraiment spéciale parce qu’elle représente en fait une référence. C’est logique dans notre exemple d’essai clinique. L’état placebo correspond à la situation où vous ne donnez pas de vrais médicaments aux gens, et c’est donc particulier. Les deux autres conditions sont définies par rapport au placebo. Dans un cas, vous remplacez le placebo par Anxifree et dans l’autre par Joyzepam.

Le tableau ci-dessus est une matrice des contrastes de traitement pour un facteur à 3 niveaux. Mais supposons que je veuille une matrice des contrastes de traitement pour un facteur à 5 niveaux ? Ce serait quelque chose comme ça :

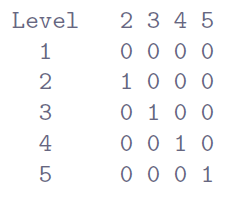
Dans cet exemple, le premier contraste est de niveau 2 comparé au niveau 1, le second contraste est de niveau 3 comparé au niveau 1, et ainsi de suite. Notez que, par défaut, le premier niveau du facteur est toujours traité comme la catégorie de base (c’est-à-dire celle qui a tous les zéros et qui n’est pas associée à un contraste explicite). Dans Jamovi vous pouvez choisie quelle catégorie est le premier niveau du facteur en manipulant l’ordre des niveaux de la variable affichée dans la fenêtre « Data Variable » (double-cliquez sur le nom de la variable dans la colonne de la feuille de calcul pour faire apparaître la fenêtre « Data Variable ».

14.7.2 Contraste de Helmert

Les contrastes de traitement sont utiles dans de nombreuses situations. Toutefois, elles sont plus sensées dans une situation où il y a vraiment une catégorie de référence, et vous voulez évaluer tous les autres groupes par rapport à cette catégorie. Dans d’autres situations, cependant, il n’existe pas de catégorie de référence et il peut être plus logique de comparer chaque groupe à la moyenne des autres groupes. C’est là que nous rencontrons les contrastes de Helmert, générés par l’option « Helmert » dans la boîte de sélection Jamovi « ANOVA » – « Contrasts ». L’idée derrière les contrastes de Helmert est de comparer chaque groupe à la moyenne des « précédents ». C’est-à-dire que le premier contraste représente la différence entre le groupe 2 et le groupe 1, le second contraste représente la différence entre le groupe 3 et la moyenne des groupes 1 et 2, etc. Cela se traduit par une matrice de contraste qui ressemble à celle-ci pour un facteur à cinq niveaux :

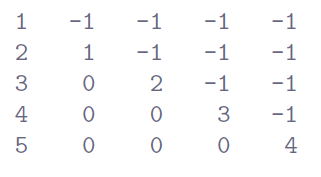
Une chose utile à propos des contrastes de Helmert est que chaque contraste est égal à zéro (c’est-à-dire que toutes les colonnes sont égales à zéro). Ceci a pour conséquence que, lorsque nous interprétons l’ANOVA comme une régression, l’intersection correspond à la grande moyenne \(\mu_{..}\) si nous utilisons les contrastes de Helmert. Comparez cela aux contrastes de traitement, dans lesquels le terme d’intersection correspond à la moyenne du groupe pour la catégorie de référence. Cette propriété peut être très utile dans certaines situations. Ce n’est pas très important si vous avez un plan équilibré, ce que nous avons supposé jusqu’à présent, mais cela s’avérera important plus tard si nous considérons les plans non équilibrées dans la Section 14.10. En fait, la principale raison pour laquelle j’ai même pris la peine d’inclure cette section est que les contrastes deviennent importants si vous voulez comprendre l’analyse de variance non équilibrée.

14.7.3 Somme des contrastes à zéro

La troisième option que je dois mentionner brièvement est celle des contrastes avec une « somme à zéro », appelés contrastes « simples » en Jamovi, qui sont utilisés pour construire des comparaisons par paires entre groupes. Plus précisément, chaque contraste code la différence entre l’un des groupes et une catégorie de base, qui dans ce cas correspond au premier groupe :

Tout comme les contrastes de Helmert, nous voyons que chaque colonne a un total à zéro, ce qui signifie que le terme d’intersection correspond à la grande moyenne lorsque ANOVA est traité comme un modèle de régression. Lorsqu’on interprète ces contrastes, il faut reconnaître que chacun de ces contrastes est une comparaison par paires entre le groupe 1 et l’un des quatre autres groupes. Plus précisément, le contraste 1 correspond à une comparaison « groupe 2 moins groupe 1 », le contraste 2 correspond à une comparaison « groupe 3 moins groupe 1 », et ainsi de suite.¹²⁸

14.7.4 Contraste optionnel en Jamovi

Jamovi est fourni également avec une variété d’options qui peuvent générer différents types de contrastes dans l’ANOVA. Celles-ci se trouvent dans l’option « Contrasts » de la fenêtre principale de l’analyse ANOVA, où les types de contraste suivants sont listés :

Type de contraste
Déviation	Comparer la moyenne de chaque niveau (sauf une catégorie de référence) à la moyenne de tous les niveaux (moyenne générale).
Simple	Tout comme les contrastes du traitement, le contraste simple compare la moyenne de chaque niveau à la moyenne d’un niveau donné. Ce type de contraste est utile lorsqu’il y a un groupe témoin. Par défaut, la première catégorie est la référence. Cependant, avec un simple contraste, l’interception est la grande moyenne de tous les niveaux des facteurs.
Différence	Compare la moyenne de chaque niveau (sauf le premier) à la moyenne des niveaux précédents. (Parfois appelé contraste Helmert inversé)
Helmert	Comparer la moyenne de chaque niveau du facteur (sauf le dernier) à la moyenne des niveaux subséquents.
Répété	Comparer la moyenne de chaque niveau (sauf le dernier) à la moyenne du niveau suivant.
Polynôme	Compare l’effet linéaire et l’effet quadratique. Le premier degré de liberté contient l’effet linéaire dans toutes les catégories ; le second degré de liberté, l’effet quadratique. Ces contrastes sont souvent utilisés pour estimer les tendances polynomiales

14.8 Tests post hoc

Il est temps de changer de sujet. Plutôt que de faire des comparaisons préétablies que vous avez testées en utilisant des contrastes, supposons que vous ayez fait votre analyse de variance et qu’il s’avère que vous avez obtenu certains effets significatifs. Étant donné que les tests F sont des tests « omnibus » qui ne testent que l’hypothèse nulle qu’il n’y a pas de différences entre les groupes, l’obtention d’un effet significatif ne vous dit pas quels groupes sont différents des autres. Nous avons discuté de cette question au chapitre 13 et, dans ce chapitre, notre solution consistait à effectuer des tests t pour toutes les paires de groupes possibles, en effectuant des corrections pour les comparaisons multiples (p. ex., Bonferroni, Holm) afin de contrôler le taux d’erreur de type I dans toutes les comparaisons. Les méthodes que nous avons utilisées au chapitre 13 ont l’avantage d’être relativement simples et d’être le genre d’outils que vous pouvez utiliser dans un grand nombre de situations différentes où vous testez plusieurs hypothèses, mais ce ne sont pas nécessairement les meilleurs choix si vous êtes intéressé à faire des tests post hoc efficaces dans un contexte ANOVA. Il existe en fait un grand nombre de méthodes différentes pour effectuer des comparaisons multiples dans la littérature statistique (Hsu 1996), et il serait au-delà de la portée d’un texte d’introduction comme celui-ci d’en discuter tous en détail.

Cela dit, il y a un outil sur lequel je veux attirer votre attention, à savoir « Honestly Significant Difference » de Tukey, ou HSD de Tukey pour faire court. Pour une fois, je vais vous épargner les formules et m’en tenir aux idées qualitatives. L’idée de base du HSD de Tukey est d’examiner toutes les comparaisons pertinentes par paires entre les groupes, et il n’est vraiment approprié d’utiliser le HSD de Tukey que si ce sont les différences par paires qui vous intéressent.¹²⁹ Par exemple, nous avons déjà effectué une analyse de variance factorielle à l’aide de l’ensemble de données du clinicaltrial.csv, et après avoir précisé un effet principal du médicament et un effet principal du traitement, nous serions intéressés par les quatre comparaisons suivantes :

• La différence de gain d’humeur entre les personnes ayant reçu Anxifree et celles ayant reçu le placebo.
• La différence de gain d’humeur entre les personnes recevant le Joyzepam et celles recevant le placebo.
• La différence de gain d’humeur entre les personnes ayant reçu Anxifree et celles ayant reçu Joyzepam.
• La différence de gain d’humeur entre les personnes traitées avec la TCC et celles qui n’ont pas reçu de thérapie.

Pour l’une ou l’autre de ces comparaisons, nous nous intéressons à la différence réelle entre les moyennes des groupes (de population). Le HSD de Tukey construit des intervalles de confiance simultanés pour ces quatre comparaisons. Ce que nous entendons par intervalle de confiance « simultané » à 95 %, c’est que, si nous devions répéter cette étude plusieurs fois, alors dans 95 % des résultats de l’étude, les intervalles de confiance contiendraient la vraie valeur pertinente. De plus, nous pouvons utiliser ces intervalles de confiance pour calculer une valeur p ajustée pour une comparaison spécifique.

La fonction TukeyHSD dans Jamovi est assez facile à utiliser. Vous spécifiez simplement les termes de modèle ANOVA pour lequel vous voulez exécuter les tests post hoc. Par exemple, si nous cherchions à effectuer des tests post hoc pour les effets principaux mais pas pour l’interaction, nous ouvririons l’option « Post Hoc Tests » dans l’écran d’analyse ANOVA, déplacerions les variables du drug et de la therapy vers la case de droite, puis sélectionnerions la case « Tukey » dans la liste des corrections post hoc qui pourraient être appliquées. La Figure 14‑24 illustre ces choix, ainsi que le tableau des résultats correspondant.

Les résultats présentés dans le tableau des résultats des « tests post hoc » sont (je l’espère) assez simples. La première comparaison, par exemple, est la différence Anxifree versus placebo, et la première partie du résultat indique que la différence observée dans les moyennes de groupe est 0,27. Le chiffre suivant est l’erreur-type pour la différence, à partir de laquelle nous pourrions calculer l’intervalle de confiance à 95 % si nous le voulions, bien que Jamovi ne propose pas actuellement cette option. Il y a ensuite une colonne avec les degrés de liberté, une colonne avec la valeur t, et enfin une colonne avec la valeur p. Pour la première comparaison, la valeur p ajustée est .21. Par contre, si vous regardez la ligne suivante, nous voyons que la différence observée entre le joyzepam et le placebo est de 1,03, et ce résultat est significatif p<.001q.

Pour l’instant, tout va bien. Qu’en est-il de la situation où votre modèle inclut des termes d’interaction ? Par exemple, l’option par défaut dans Jamovi est de tenir compte de la possibilité qu’il y ait une interaction entre le médicament et la thérapie. Si c’est le cas, le nombre de comparaisons par paires dont nous avons besoin va considérer commence à augmenter.

Figure 14‑24 : Test post-hoc Tukey HSD dans l’ANOVA factorielle Jamovi, sans terme d’interaction

Comme par le passé, nous devons considérer les trois comparaisons pertinentes à l’effet principal de drug et la comparaison pertinente à l’effet principal du therapy. Mais, si nous voulons envisager la possibilité d’une interaction significative (et essayer de trouver les différences de groupe qui sous-tendent cette interaction significative), nous devons inclure des comparaisons telles que les suivantes :

• La différence de gain d’humeur entre les personnes ayant reçu Anxifree et traitées avec la TCC et les personnes ayant reçu le placebo et traitées avec la TCC.
• La différence de gain d’humeur entre les personnes ayant reçu Anxifree et celles n’ayant reçu aucun traitement, et celles ayant reçu le placebo et n’ayant reçu aucun traitement.
• Etc.

Il y a beaucoup de ces comparaisons dont vous devez tenir compte. Ainsi, lorsque nous effectuons l’analyse post hoc de Tukey pour ce modèle ANOVA, nous constatons qu’il a fait beaucoup de comparaisons par paires (19 au total), comme le montre la Figure 14‑25. Vous pouvez voir qu’il ressemble beaucoup à ce qu’il était avant, mais avec beaucoup plus de comparaisons faites.

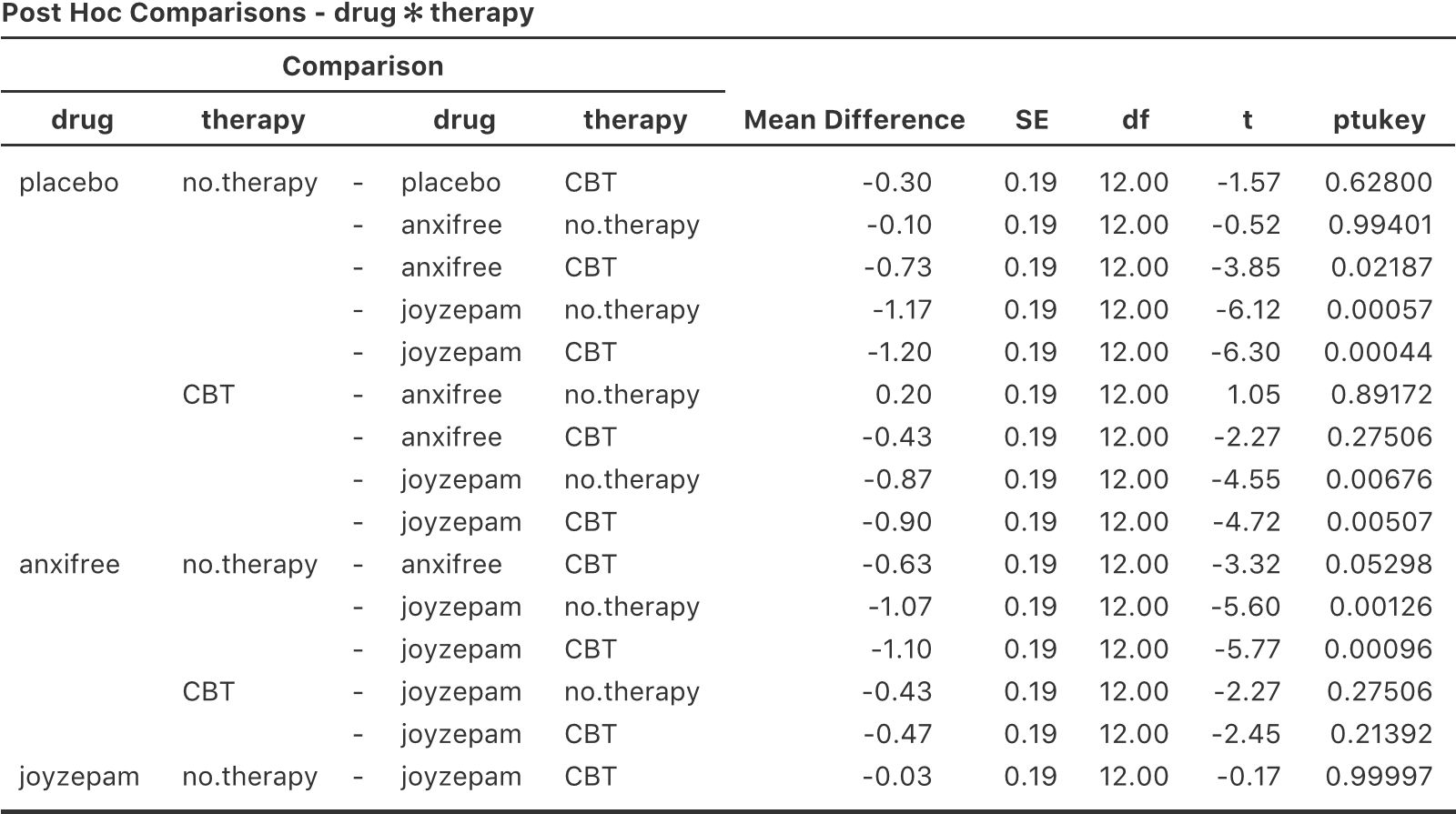
Figure 14‑25 : Test post hoc de Tukey HSD dans l’ANOVA factorielle de Jamovi avec un terme d’interaction

14.9 La méthode des comparaisons planifiées

Dans le prolongement des sections précédentes sur les contrastes et les tests post hoc dans ANOVA, je pense que la méthode des comparaisons planifiées est suffisamment importante pour mériter une discussion rapide. Dans nos discussions sur les comparaisons multiples, dans la section précédente et au chapitre 13, j’ai supposé que les tests que vous voulez effectuer sont vraiment post hoc. Par exemple, dans notre exemple de médicaments ci-dessus, vous pensiez peut-être que les médicaments auraient tous des effets différents sur l’humeur (c.-à-d. que vous avez émis l’hypothèse d’un effet principal du médicament), mais vous n’aviez aucune hypothèse précise sur la façon dont ils diffèreraient, ni aucune idée réelle des comparaisons par paires qu’il serait utile d’examiner. Si c’est le cas, alors vous devez vraiment recourir à quelque chose comme le HSD de Tukey pour faire vos comparaisons par paires.

La situation est assez différente, cependant, si vous aviez réellement des hypothèses spécifiques sur lesquelles les comparaisons sont intéressantes, et que vous n’avez jamais eu l’intention de regarder d’autres comparaisons que celles que vous avez spécifiées à l’avance. Quand c’est vrai, et si vous vous en tenez honnêtement et rigoureusement à vos nobles intentions de ne pas faire d’autres comparaisons (même lorsque les données semblent vous montrer des effets délicieusement significatifs pour des choses pour lesquelles vous n’aviez pas de test d’hypothèse), alors cela n’a pas vraiment de sens de faire quelque chose comme le HSD de Tukey, car il apporte des corrections pour toute une série de comparaisons que vous n’avez jamais voulu et auxquelles vous ne vous êtes jamais intéressés. Dans ces circonstances, vous pouvez effectuer un nombre (limité) de tests d’hypothèse sans avoir à faire d’ajustement pour plusieurs tests. Cette situation est connue sous le nom de méthode des comparaisons planifiées, et elle est parfois utilisée dans les essais cliniques. Cependant, il n’est pas possible de poursuivre cette réflexion dans ce livre d’introduction, mais au moins, vous savez que cette méthode existe !

14.10 ANOVA Factorielle 3 : plans non équilibrés

ANOVA factorielle est une chose très pratique à connaître. C’est l’un des outils standard utilisés pour analyser les données expérimentales depuis de nombreuses décennies, et vous constaterez que vous ne pouvez pas lire plus de deux ou trois articles en psychologie sans y trouver une analyse de variance. Cependant, il y a une énorme différence entre les analyses de variance que vous verrez dans beaucoup d’articles scientifiques réels et les analyses de variance que j’ai décrites jusqu’ici. Dans la vie réelle, nous avons rarement la chance d’avoir des plans parfaitement équilibrés. Pour une raison ou une autre, il est typique de se retrouver avec plus d’observations dans certaines cellules que dans d’autres. Ou, pour le dire autrement, nous avons un plan non équilibré.

Les plans non équilibrés doivent être traités avec beaucoup plus de soin que les plans équilibrés, et la théorie statistique qui les sous-tend est beaucoup plus confuse. C’est peut-être une conséquence de ce désordre ou un manque de temps, mais d’après mon expérience, les cours de premier cycle sur les méthodes de recherche en psychologie ont tendance à ignorer complètement cette question. Beaucoup de manuels de statistiques ont aussi tendance à l’ignorer. Le résultat de tout cela, je pense, est que beaucoup de chercheurs actifs dans le domaine ne savent pas vraiment qu’il existe plusieurs « types » d’analyses de variance de pour les plans non équilibrés, et ils produisent des réponses très différentes. En fait, en lisant la littérature psychologique, je suis un peu étonné du fait que la plupart des gens qui rapportent les résultats d’une analyse de variance factorielle non équilibrée ne vous donnent pas assez de détails pour reproduire cette analyse. Je soupçonne secrètement que la plupart des gens ne se rendent même pas compte que leur progiciel statistique prend un grand nombre de décisions importantes d’analyse de données en leur nom. C’est un peu terrifiant quand on y pense. Donc, si vous voulez éviter de confier le contrôle de l’analyse de vos données à un logiciel idiot, lisez ce qui suit.

14.10.1 Les données sur le café

Comme d’habitude, nous travaillerons avec des données pour nous aider. Le fichier coffee.csv contient un ensemble de données hypothétiques qui produit une ANOVA 3x2 non équilibrée. Supposons que nous voulions savoir si la tendance des gens à bavarder lorsqu’ils prennent trop de café est purement un effet du café lui-même, ou s’il y a un effet du lait et du sucre que les gens ajoutent au café. Supposons que nous prenions 18 personnes et leur donnions du café à boire. La quantité de café / caféine a été maintenue constante, et nous avons fait varié si le lait a été ajouté ou non, donc le lait (milk) est un facteur binaire avec deux niveaux, « oui » et « non ». Nous avons également varié le type de sucre en cause. Le café peut contenir du « vrai » sucre ou du « faux » sucre (c’est-à-dire un édulcorant artificiel), ou il peut en contenir « aucun », de sorte que la variable sucre (sugar) est un facteur à trois niveaux. Notre variable de résultat est une variable continue qui fait vraisemblablement référence à une mesure psychologiquement raisonnable du babillage (babble) de quelqu’un. Les détails n’ont pas vraiment d’importance pour notre but. Jetez un coup d’œil aux données du côté tableur de Jamovi, comme dans la Figure 14‑26.

En examinant le tableau des moyennes de la Figure 14‑26, nous avons l’impression qu’il y a des différences entre les groupes. C’est particulièrement vrai lorsque nous comparons ces moyennes aux écarts-types de la variable babble. Dans l’ensemble des groupes, cet écart-type varie de 0,14 à 0,71, ce qui est assez faible par rapport aux différences dans les moyennes des groupes.¹³⁰ Bien que cela puisse sembler à première vue une analyse de variance factorielle simple, un problème se pose lorsque nous examinons le nombre d’observations que nous avons dans chaque groupe. Voir les différents N pour les différents groupes illustrés à la Figure 14‑26 Cela va à l’encontre de l’une de nos hypothèses initiales, à savoir que le nombre de personnes dans chaque groupe est le même. Nous n’avons pas vraiment discuté de la façon de gérer cette situation.

Figure 14‑26 : L’ensemble de données de coffee.csv dans Jamovi, avec des informations descriptives agrégées par niveaux de facteurs

14.10.2 Il n’existe pas d’ANOVA standard pour les conceptions non équilibrées.

Des plans non équilibrées nous amènent à la découverte quelque peu troublante qu’il n’y a pas vraiment une seule chose que nous pourrions appeler une ANOVA standard. En fait, il s’avère qu’il y a trois¹³¹façons fondamentalement différentes d’utiliser une ANOVA dans un plan non équilibré. Si vous avez un design équilibré, les trois versions donnent des résultats identiques, avec des sommes de carrés, de valeurs F, etc. conformes aux formules que j’ai données au début du chapitre. Cependant, lorsque votre conception est déséquilibrée, ils ne donnent pas les mêmes réponses. En outre, elles ne sont pas toutes adaptées à chaque situation. Certaines méthodes seront plus appropriées à votre situation que d’autres. Compte tenu de tout cela, il est important de comprendre quels sont les différents types d’ANOVA et en quoi ils diffèrent les uns des autres.

Le premier type d’ANOVA est conventionnellement appelé somme des carrés de type I. Je suis sûr que vous pouvez deviner comment s’appellent les deux autres. La partie « somme des carrés » du nom a été introduite par le progiciel statistique SAS et est devenue une nomenclature standard, mais c’est un peu trompeur à certains égards. Je pense que la logique pour les désigner comme différents types de somme de carrés est que, lorsqu’on examine les tableaux ANOVA qu’ils produisent, la principale différence dans les chiffres est la valeur SS. Les degrés de liberté ne changent pas, les valeurs MS sont toujours définies comme SS divisées par df, etc. Cependant, la terminologie se trompe parce qu’elle cache la raison pour laquelle les valeurs SS sont différentes les unes des autres. À cette fin, il est beaucoup plus utile de considérer les trois différents types d’analyses de variance comme trois stratégies différentes de vérification des hypothèses. Ces différentes stratégies mènent à des valeurs SS différentes, bien sûr, mais c’est la stratégie qui est importante ici, pas les valeurs SS elles-mêmes. Rappelons à la section 14.6 qu’il est préférable de considérer tout test F particulier comme une comparaison entre deux modèles linéaires. Ainsi, lorsque vous regardez un tableau ANOVA, il est utile de se rappeler que chacun de ces tests F correspond à une paire de modèles qui sont comparés. Cela nous amène naturellement à la question de savoir quelle paire de modèles est comparée. C’est la différence fondamentale entre les types I, II et III d’ANOVA : chacun correspond à une manière différente de choisir les paires de modèles pour les tests.

14.10.3 Somme des carrés de type I

La méthode de type I est parfois appelée somme « séquentielle » des carrés, car elle consiste à ajouter au modèle un des termes à la fois. Prenons les données sur le café, par exemple. Supposons que nous voulions exécuter la 3 x 2 ANOVA factorielle complète, y compris les termes d’interaction. Le modèle complet contient la variable de résultat babble, les variables prédicteurs sugar et milk, et l’interaction sugar*milk. Ceci peut s’écrire babble ~ sugar + milk + sugar* milk. La stratégie de type I construit ce modèle séquentiellement, à partir du modèle le plus simple possible et en ajoutant progressivement des termes.

Le modèle le plus simple possible pour les données serait un modèle dans lequel ni le lait ni le sucre n’auraient d’effet sur le babillage. Le seul terme qui serait inclus dans un tel modèle est l’intersection, écrit comme babble ~ 1, c’est notre hypothèse nulle initiale. Le modèle le plus simple suivant pour les données serait un modèle dans lequel un seul des deux effets principaux est inclus. Dans les données sur le café, il y a deux choix possibles, car nous pourrions choisir d’ajouter du lait en premier ou du sucre en premier. L’ordre s’avère important, comme nous le verrons plus tard, mais pour l’instant, faisons un choix arbitraire et choisissons le sucre. Ainsi, le deuxième modèle de notre séquence de modèles est babble ~ sugar, et il forme l’hypothèse alternative pour notre premier test. Nous avons maintenant notre premier test d’hypothèse :

• Modèle d’hypothèse nulle : babble ~ 1
  
• Modèle alternatif : babble ~ sugar

Cette comparaison forme notre test d’hypothèse sur l’effet principal du sugar. L’étape suivante dans notre exercice de construction de modèle est d’ajouter l’autre terme d’effet principal, donc le modèle suivant dans notre séquence est babble ~ sugar + milk. Le deuxième test d’hypothèse est ensuite formé en comparant les deux modèles suivants :

• Modèle d’hypothèse nulle : babble ~ sugar
  
• Modèle alternatif : babble ~ sugar + milk

Cette comparaison forme notre test d’hypothèse sur l’effet principal de millk. Dans un sens, cette approche est très élégante : l’hypothèse alternative du premier test forme l’hypothèse nulle pour le second. C’est dans ce sens que la méthode de type I est strictement séquentielle. Chaque test s’appuie directement sur les résultats du dernier. Cependant, dans un autre sens, c’est très peu élégant, parce qu’il y a une forte asymétrie entre les deux tests. Le test de l’effet principal de sugar (le premier test) ignore complètement le lait, alors que le test de l’effet principal du milk (le second test) prend en compte le sugar. En tout cas, le quatrième modèle de notre séquence est maintenant le modèle complet, babble ~ sugar + milk + sugar*milk, et le test d’hypothèse correspondant est :

• Modèle d’hypothèse nulle : babble ~ sugar + milk
• Modèle alternatif : babble ~ sugar + milk + sugar*milk

La somme des carrés de type III est la méthode de test d’hypothèse par défaut utilisée par Jamovi ANOVA, donc pour exécuter une analyse de somme de carrés de type I, nous devons sélectionner « Type 1 » dans la boîte de sélection « Somme des carrés » dans les options Jamovi « ANOVA » – « Model ». Cela nous donne le tableau ANOVA illustré à la figure 14.27.

Figure 14‑27 : Tableau des résultats ANOVA utilisant la somme des carrés de type I dans Jamovi

Le gros problème avec l’utilisation de la somme des carrés de type I est le fait que cela dépend vraiment de l’ordre dans lequel vous entrez les variables. Pourtant, dans de nombreuses situations, le chercheur n’a aucune raison de préférer un ordre à un autre. C’est probablement le cas pour notre problème du lait et du sucre. Doit-on ajouter du lait d’abord ou du sucre d’abord ? C’est exactement aussi arbitraire qu’une question d’analyse de données sur la préparation du café. En fait, il y a peut-être des gens qui ont des opinions fermes sur l’ordre, mais il est difficile d’imaginer une réponse fondée sur des principes à cette question. Pourtant, regardez ce qui se passe lorsque nous changeons l’ordre, comme dans la Figure 14‑28.

Figure 14‑28 : Tableau des résultats de l’analyse de variance utilisant la somme des carrés de type I dans le Jamovi, mais avec les facteurs saisis dans un ordre différent (milk d’abord).

Les valeurs p des deux principaux effets ont changé, et de façon assez spectaculaire. Entre autres choses, l’effet de milk est devenu significatif (bien qu’il faille éviter d’en tirer de fortes conclusions, comme je l’ai mentionné précédemment). Laquelle de ces deux analyses de variance doit-on déclarer ? Ce n’est pas immédiatement évident.

Lorsqu’on regarde les tests d’hypothèse utilisés pour définir le « premier » effet principal et le « second », il est clair qu’ils sont qualitativement différents l’un de l’autre. Dans notre premier exemple, nous avons vu que le test de l’effet principal de sugar ignore complètement milk, alors que le test de l’effet principal de milk prend en compte sugar. En tant que telle, la stratégie d’essai du type I traite vraiment le premier effet principal comme s’il avait une sorte de primauté théorique sur le second. D’après mon expérience, il y a très rarement, voire jamais, une primauté théorique de ce genre qui justifierait de traiter deux effets principaux de façon asymétrique.

La conséquence de tout cela est que les tests du type I présentent très rarement un grand intérêt, et nous devrions donc passer aux essais du type II et du type III.

14.10.4 Type III somme des carrés

Après avoir terminé de parler des tests du type I, vous pourriez penser que la chose naturelle à faire ensuite serait de parler des tests du type II. Cependant, je pense qu’il est en fait un peu plus naturel de discuter des tests de type III (qui sont simples et qui sont par défaut dans l’ANOVA Jamovi) avant de parler des essais de type II (qui sont plus difficiles). L’idée de base des essais du type III est extrêmement simple. Quel que soit le terme que vous essayez d’évaluer, exécutez le test F dans lequel l’hypothèse alternative correspond au modèle ANOVA complet tel que spécifié par l’utilisateur, et le modèle d’hypothèse nulle ne fait que supprimer ce terme que vous testez. Dans l’exemple du café, où notre modèle complet était babble ~ sugar + milk + sugar* milk, le test pour un effet principal de sugar correspondrait à une comparaison entre les deux modèles suivants :

• Modèle d’hypothèse nulle : babble ~ milk + sugar* milk
• Modèle alternatif : babble ~ sugar + milk + sugar* milk

De même, l’effet principal du lait est évalué en testant le modèle complet par rapport à un modèle nul qui supprime le terme lait, comme ça :

• Modèle d’hypothèse nulle : babble ~ sugar + sugar* milk
• Modèle alternatif : babble ~ sugar + milk + sugar* milk

Enfin, l’interaction sucre*lait est évaluée exactement de la même manière. Une fois de plus, nous testons le modèle complet par rapport à un modèle nul qui supprime le terme d’interaction sucre*lait, comme ça :

• Modèle d’hypothèse nulle : babble ~ sugar + milk
• Modèle alternatif : babble ~ sugar + milk + sugar* milk

L’idée de base se généralise aux ANOVA d’ordre supérieur. Par exemple, supposons que nous essayions d’exécuter une analyse de variance avec trois facteurs, A, B et C, et que nous voulions considérer tous les effets principaux possibles et toutes les interactions possibles, y compris l’interaction triple A*B*C. Le tableau ci-dessous vous montre à quoi ressemblent les tests du type III dans cette situation :

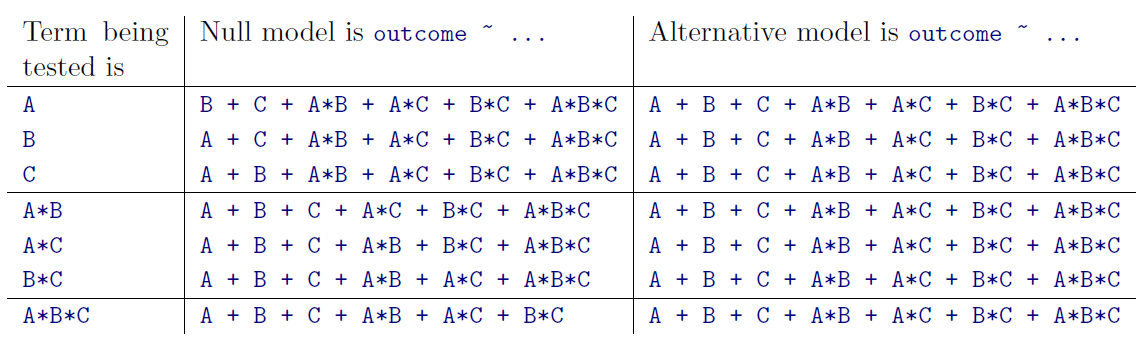
Aussi moche que ce tableau ait l’air, il est assez simple. Dans tous les cas, l’hypothèse alternative correspond au modèle complet qui contient trois termes d’effets principaux (p. ex. A), trois interactions (p. ex. A*B) et une interaction triple (p. ex. A*B*C). Le modèle de l’hypothèse nulle contient toujours 6 de ces 7 termes, et celui qui manque est celui dont nous essayons de tester la signification.

Au premier abord, les tests de type III semblent être une bonne idée. Premièrement, nous avons éliminé l’asymétrie qui nous causait des problèmes lors de l’exécution des tests de type I. Et parce que nous traitons maintenant tous les termes de la même façon, les résultats des tests d’hypothèse ne dépendent pas de l’ordre dans lequel nous les spécifions. C’est définitivement une bonne chose. Cependant, l’interprétation des résultats des tests pose un gros problème, surtout en ce qui concerne les effets principaux. Pensez aux données sur le café. Supposons qu’il s’avère que l’effet principal de milk ne soit pas significatif selon les tests du type III. Ce que cela nous dit, c’est que babble ~ sugar + sugar*milk est un meilleur modèle pour les données que le modèle complet. Mais qu’est-ce que ça veut dire ? Si le terme d’interaction sugar*milk était également non significatif, nous serions tentés de conclure que les données nous disent que la seule chose qui compte est le sucre. Mais supposons que nous ayons un terme d’interaction significatif, mais un effet principal non significatif du lait. Dans ce cas, faut-il supposer qu’il y a vraiment un « effet du sucre », une « interaction entre le lait et le sucre », mais pas un « effet du lait » ? Cela semble fou. La bonne réponse doit simplement être qu’il est inutile de parler de l’effet principal¹³² si l’interaction est importante. En général, c’est ce que la plupart des statisticiens nous conseillent de faire, et je pense que c’est le bon conseil. Mais s’il est vraiment inutile de parler d’effets principaux non significatifs en présence d’une interaction significative, il n’est pas du tout évident de savoir pourquoi les essais de type III devraient permettre à l’hypothèse nulle de s’appuyer sur un modèle qui inclut l’interaction mais omet un des principaux effets qui la composent. Lorsqu’elles sont ainsi caractérisées, les hypothèses nulles n’ont vraiment aucun sens.

Nous verrons plus loin que les tests de type III peuvent être utiles dans certains contextes, mais examinons d’abord le tableau des résultats d’ANOVA en utilisant la somme des carrés de type III, voir Figure 14‑29.

Mais attention, l’une des caractéristiques perverses de la stratégie d’essais du type III est que les résultats dépendent généralement des contrastes que vous utilisez pour coder vos facteurs (voir la section 14.7 si vous avez oublié quels sont les différents types de contrastes).¹³³

D’accord, donc si les valeurs p qui ressortent généralement des analyses de type III (mais pas dans Jamovi) sont si sensibles au choix des contrastes, est-ce que cela signifie que les essais de type III sont essentiellement arbitraires et ne sont pas fiables ? Dans une certaine mesure, c’est vrai, et lorsque nous parlons des tests de type II, nous verrons que les analyses de type II évitent complètement ce caractère arbitraire, mais je pense que c’est une conclusion trop forte.

Figure 14‑29 : Tableau des résultats ANOVA utilisant la somme des carrés de type III in Jamovi

Tout d’abord, il est important de reconnaître que certains choix de contrastes produiront toujours les mêmes réponses (ah, c’est donc ce qui se passe dans Jamovi). Il est particulièrement important de noter que si les colonnes de notre matrice de contraste ont toutes une somme à zéro, l’analyse de type III donnera toujours les mêmes réponses.

14.10.5 Type II somme des carrés

Bien, nous avons vu des essais de type I et III maintenant, et les deux sont assez simples. Les essais de type I sont effectués en ajoutant progressivement un des termes à la fois, tandis que les essais de type III sont effectués en prenant le modèle complet et en regardant ce qui se passe lorsque vous retirez chaque terme. Cependant, les deux peuvent avoir certaines limites. Les essais de type I dépendent de l’ordre dans lequel vous entrez les termes, et les essais de type III dépendent de la façon dont vous codez vos contrastes. Les essais du type II sont un peu plus difficiles à décrire, mais ils évitent ces deux problèmes et, par conséquent, ils sont un peu plus faciles à interpréter.

Les essais du type II sont globalement similaires aux essais du type III. Commencer par un modèle « complet » et tester un terme particulier en le supprimant de ce modèle. Cependant, les essais de type II sont basés sur le principe de marginalité qui stipule que vous ne devez pas omettre un terme d’ordre inférieur de votre modèle s’il y a des termes d’ordre supérieur qui en dépendent. Ainsi, par exemple, si votre modèle contient l’interaction A*B (un terme de 2e ordre), alors il devrait contenir les effets principaux A et B (termes de 1er ordre). De même, s’il contient un terme d’interaction triple A*B*C, alors le modèle doit également inclure les principaux effets A, B et C ainsi que les interactions plus simples A*B, A*C et B*C. Les essais de type III violent systématiquement le principe de marginalité. Par exemple, examinons le test de l’effet principal de A dans le contexte d’une analyse de variance à trois facteurs qui comprend tous les termes d’interaction possibles. Selon les essais de type III, nos modèles nuls et alternatifs le sont :

• Modèle d’hypothèse nulle : outcome ~ B + C + A*B + A*C + B*C + A*B*C
• Modèle alternatif : outcome ~ A + B + C + C + A*B + A*C + B*C + A*B*C

Notez que l’hypothèse nulle omet A, mais inclut A*B, A*C et A*B*C dans le modèle. D’après les tests du type II, ce n’est pas un bon choix d’hypothèse nulle. Ce que nous devrions plutôt faire, si nous voulons vérifier l’hypothèse nulle selon laquelle A n’est pas pertinent pour notre variable résultat, est de spécifier l’hypothèse nulle qui est le modèle le plus compliqué qui ne repose d’aucune façon sur A, même dans une interaction. L’hypothèse alternative correspond à ce modèle d’hypothèse nulle plus un terme d’effet principal de A. C’est beaucoup plus proche de ce que la plupart des gens penseraient intuitivement d’un « effet principal de A», et elle donne ce qui suit comme notre test de Type II de l’effet principal de A :¹³⁴

• Modèle nul : outcome ~ B + C + B*C
• Modèle alternatif : outcome ~ A + B + C + C + B*C

Quoi qu’il en soit, pour vous donner une idée du déroulement des essais de type II, voici le tableau complet de modèles qui serait appliqué dans une ANOVA factorielle à trois facteurs :

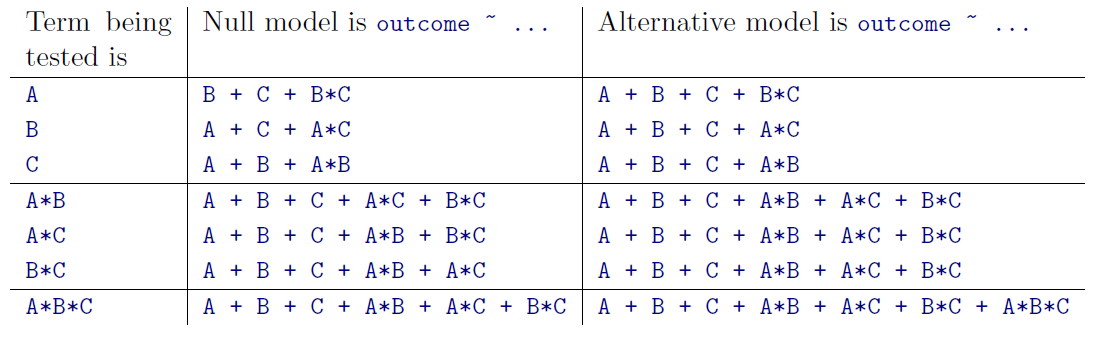
Dans le contexte de l’analyse de variance à deux facteurs que nous avons utilisée dans les données sur le café, les tests d’hypothèse sont encore plus simples. L’effet principal de sugar correspond à un test F comparant ces deux modèles :

• Modèle d’hypothèse nulle : babble ~ milk
  
• Modèle alternatif : babble ~ sugar + milk

Le test de l’effet principal de milk est le suivant

• Modèle d’hypothèse nulle : babble ~ sugar
  
• Modèle alternatif : babble ~ sugar + milk

Enfin, le test pour l’interaction sugar*milk est :

• Modèle d’hypothèse nulle : babble ~ sugar + milk
  
• Modèle alternatif : babble ~ sugar + milk + sugar*mil

L’exécution des tests est à nouveau simple. Il suffit de sélectionner « Type 2 » dans la boîte de sélection « Somme des carrés »’ dans les options « ANOVA » - « Modèle » de Jamovi, ce qui nous donne le tableau ANOVA montré dans la Figure 14.30.

Figure 14‑30 : Tableau des résultats ANOVA utilisant la somme des carrés de type II dans Jamovi

Les essais du type II présentent certains avantages évidents par rapport aux essais du type I et du type III. Ils ne dépendent pas de l’ordre dans lequel vous spécifiez les facteurs (contrairement au Type I), et ils ne dépendent pas des contrastes que vous utilisez pour spécifier vos facteurs (contrairement au Type III). Et bien que les opinions puissent diverger sur ce dernier point, et cela dépendra certainement de ce que vous essayez de faire avec vos données, je pense que les tests d’hypothèse qu’ils spécifient sont plus susceptibles de correspondre à quelque chose qui vous préoccupe vraiment. Par conséquent, je trouve qu’il est généralement plus facile d’interpréter les résultats d’un essai du type II que ceux d’un essai du type I ou III. Pour cette raison, mon conseil provisoire est que, si vous ne pouvez pas penser à des comparaisons de modèles évidentes qui correspondent directement à vos questions de recherche, mais que vous voulez quand même exécuter une analyse de variance dans un plan non équilibré, les tests de type II sont probablement un meilleur choix que de type I ou III.¹³⁵

14.10.6 Tailles de l’effet (et sommes non additives de carrés)

Jamovi fournit également les tailles d’effet \(\eta^{2}\) et \(\eta^{2}\) partiel lorsque vous sélectionnez ces options, comme dans la Figure 14‑30. Cependant, quand vous avez un plan non équilibré, c’est un peu plus de complexité.

Si vous vous souvenez de nos premières discussions sur l’analyse de variance, l’une des idées clés derrière les sommes des calculs des carrés est que si nous additionnons tous les termes SS associés aux effets dans le modèle, et que nous ajoutons cela aux SS résiduels, ils sont censés s’additionner pour former la somme totale des carrés. Et, en plus de cela, l’idée derrière \(\eta^{2}\) est que, parce que vous divisez l’une des SS par la SS totale, une valeur \(\eta^{2}\) peut être interprétée comme la proportion de la variance représentée par un terme particulier. Mais ce n’est pas aussi simple dans les plans non équilibrés parce qu’une partie de la variance est « manquante ».

Cela semble un peu étrange à première vue, mais voici pourquoi. Lorsque vous avez des plans non équilibrés, vos facteurs sont corrélés les uns avec les autres, et il devient difficile de faire la différence entre l’effet du facteur A et l’effet du facteur B. Dans le cas extrême, supposons que nous ayons exécuté un plan 2x2 où le nombre de participants dans chaque groupe était le suivant :

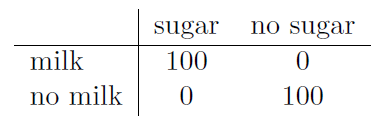
Nous avons ici un plan spectaculairement déséquilibré : 100 personnes prennent du lait et du sucre, 100 personnes ne prennent ni lait ni sucre, et c’est tout. Il y a 0 personne avec du lait et sans sucre, et 0 personne avec du sucre mais sans lait. Supposons maintenant que, lorsque nous avons recueilli les données, il s’est avéré qu’il existe une différence importante (et statistiquement significative) entre le groupe « lait et sucre » et le groupe « sans lait et sans sucre ». S’agit-il d’un effet principal du sucre ? Un effet principal du lait ? Ou une interaction ? C’est impossible à dire, car la présence de sucre est parfaitement associée à la présence de lait. Supposons maintenant que le design ait été un peu plus équilibré :

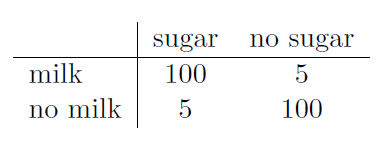
Cette fois-ci, il est techniquement possible de faire la distinction entre l’effet du lait et l’effet du sucre, parce que nous avons quelques personnes qui ont l’un mais pas l’autre. Cependant, il sera encore assez difficile de le faire, car l’association entre le sucre et le lait est encore extrêmement forte, et il y a si peu d’observations dans deux des groupes. Encore une fois, nous sommes très susceptibles d’être dans une situation où nous savons que les variables prédicteurs (sugar et milk) sont liées au résultat (babble), mais nous ne savons pas si la nature de cette relation est un effet principal de l’un ou l’autre prédicteur, ou l’interaction.

Cette incertitude est à l’origine de la variance manquante. La variance « manquante » correspond à la variation de la variable des résultats qui est clairement attribuable aux prédicteurs, mais nous ne savons pas lequel des effets du modèle est responsable. Lorsque vous calculez la somme des carrés de type I, aucune variance ne disparaît jamais. La nature séquentielle de la somme des carrés de type I signifie que l’analyse de variance attribue automatiquement cette variance aux effets qui sont entrés en premier. Toutefois, les essais de type II et de type III sont plus conservateurs. La variance qui ne peut pas être clairement attribuée à un effet spécifique n’est attribuée à aucun d’entre eux, et elle disparaît.

14.11 Résumé

• ANOVA factorielle avec des plans équilibrés, sans interactions (section 14.1) et avec interactions incluses (section 14.2)
• Taille de l’effet, moyennes estimées et intervalles de confiance dans une analyse de variance factorielle (section 14.3)
• Vérification des hypothèses dans l’analyse de variance (Section 14.4)
• Analyse de la covariance (ANCOVA) (Section 14.5)
• Comprendre le modèle linéaire sous-jacent à l’analyse de variance, y compris les différents contrastes (sections 14.6 et 14.7)
• Tests post hoc utilisant le HSD de Tukey (section 14.8) et un bref commentaire sur les comparaisons prévues (section 14.9)
• ANOVA d’usine avec des conceptions non équilibrées (Section 14.10)

References

Everitt, Brian S. 1996. Making Sense of Statistics in Psychology: A Second-Level Course. Making Sense of Statistics in Psychology: A Second-Level Course. New York, NY, US: Oxford University Press.

Hsu, Jason. 1996. Multiple Comparisons: Theory and Methods. London: Chapman and Hall/CRC.

---

121. Ndt. Ici les auteurs considèrent la relation entre les facteurs et non celle avec les sujets. Les sujets sont bien emboités dans le croisement des deux facteurs.↩︎

122. Ce qu’il y a de bien avec la notation par indice, c’est qu’elle généralise bien. Si notre expérience avait impliqué un troisième facteur, nous pourrions simplement ajouter un troisième indice. En principe, la notation s’étend à autant de facteurs que vous voudrez bien inclure, mais dans ce livre, nous considérerons rarement des analyses impliquant plus de deux facteurs, et jamais plus de trois.↩︎

123. Techniquement, la marginalisation n’est pas tout à fait identique à une moyenne régulière. Il s’agit d’une moyenne pondérée qui tient compte de la fréquence des différents événements sur lesquels vous faites la moyenne. Cependant, dans un plan équilibré, toutes les fréquences de nos cellules sont égales par définition, de sorte que les deux sont équivalentes. Nous discuterons des plans déséquilibrés plus tard, et lorsque nous le ferons, vous verrez que tous nos calculs deviennent un véritable casse-tête. Mais ignorons cela pour l’instant.↩︎

124. Traduction langage courant: « la moins ennuyeuse ».↩︎

125. Vous l’avez peut-être déjà remarqué en regardant l’analyse des effets principaux dans Jamovi que nous avons décrite plus haut. Pour les besoins des explications dans ce livre, j’ai supprimé la composante d’interaction du modèle précédent pour garder les choses propres et simples.↩︎

126. Ce chapitre semble établir un nouveau record pour le nombre de choses différentes que la lettre R peut représenter. Jusqu’à présent, R fait référence au progiciel, au nombre de lignes de notre tableau de moyennes, aux résidus dans le modèle et maintenant au coefficient de corrélation dans une régression. Désolée. Nous n’avons clairement pas assez de lettres dans l’alphabet. Cependant, j’ai essayé d’être assez clair sur ce à quoi R fait référence dans chaque cas.↩︎

127. Impossible à croire, je dirais. L’artificialité de cet ensemble de données commence vraiment à se manifester !↩︎

128. Je vous entends demander : quelle est la différence entre le traitement et les contrastes simples ? Eh bien, à titre d’exemple, considérons un effet principal de genre, avec m=0 et f=1. Le coefficient correspondant au contraste du traitement mesurera la différence de moyenne entre les femmes et les hommes, et l’intersection sera la moyenne des hommes. Cependant, avec un simple contraste, c’est-à-dire m=-1 et f=1, l’intersection est la moyenne des moyennes et l’effet principal est la différence entre la moyenne de chaque groupe et l’intersection.↩︎

129. Si, par exemple, vous souhaitez savoir si le groupe A est significativement différent de la moyenne du groupe B et du groupe C, vous devez utiliser un outil différent (par exemple, la méthode de Scheffe, qui est plus conservatrice, et qui dépasse le cadre du présent livre). Cependant, dans la plupart des cas, vous êtes probablement intéressé par les différences de groupes par paires, donc le HSD de Tukey est une chose assez utile à connaître.↩︎

130. Cet écart dans les écarts-types pourrait (et devrait) vous amener à vous demander si nous avons une violation de l’hypothèse d’homogénéité de la variance. Je vais laisser au lecteur le soin de vérifier cela à l’aide de l’option de test de Levene.↩︎

131. En fait, c’est un mensonge. Les analyses de variance peuvent varier d’autres façons que celles dont j’ai parlé dans ce livre. Par exemple, j’ai complètement ignoré la différence entre les modèles à effets fixes dans lesquels les niveaux d’un facteur sont « fixés » par l’expérimentateur ou le monde, et les modèles à effets aléatoires dans lesquels les niveaux sont des échantillons aléatoires d’une population plus large de niveaux possibles (ce livre ne couvre que les modèles à effets fixes). Ne faites pas l’erreur de penser que ce livre, ou tout autre, vous dira « tout ce que vous devez savoir » sur les statistiques, pas plus qu’un seul livre ne pourrait vous dire tout ce que vous devez savoir en psychologie, en physique ou en philosophie. La vie est trop compliquée pour que cela soit vrai. Mais que cela ne soit pas une cause de désespoir. La plupart des chercheurs s’en sortent avec une connaissance pratique basique d’ANOVA qui ne va pas plus loin que ce livre. Je veux juste que vous gardiez à l’esprit que ce livre n’est que le début d’une très longue histoire, pas l’histoire entière.↩︎

132. Ou, à tout le moins, rarement d’intérêt.↩︎

133. Cependant, dans Jamovi les résultats pour la somme des carrés de l’ANOVA Type III sont les mêmes quel que soit le contraste choisi, donc Jamovi fait évidemment quelque chose de différent !↩︎

134. Notez, bien sûr, que cela dépend du modèle que l’utilisateur a spécifié. Si le modèle ANOVA original ne contient pas de terme d’interaction pour B*C, il est évident qu’il n’apparaîtra ni dans la valeur nulle ni dans l’alternative. Mais c’est vrai pour les types I, II et III. Ils n’incluent jamais de termes que vous n’avez pas inclus, mais ils font des choix différents sur la façon de construire des tests pour ceux que vous avez inclus.↩︎

135. Je trouve amusant de constater que la valeur par défaut de R est Type I et que la valeur par défaut de SPSS et Jamovi est Type III. Ni l’un ni l’autre ne m’attire tant que ça. Par ailleurs, je trouve déprimant de constater que presque personne dans la littérature psychologique ne se donne la peine de signaler le type de tests qu’ils ont effectués, encore moins l’ordre des variables (pour le type I) ou les contrastes utilisés (pour le type III). Souvent, ils ne signalent pas non plus les logiciels qu’ils ont utilisés. La seule façon de comprendre ce que les gens rapportent habituellement est d’essayer de deviner à partir d’indices annexes quel logiciel ils utilisaient, et de supposer qu’ils n’ont jamais modifié les paramètres par défaut. S’il vous plaît, ne faites pas ça ! Maintenant que vous connaissez ces problèmes, veillez à indiquer le logiciel que vous avez utilisé, et si vous déclarez des résultats ANOVA pour des données non équilibrées, puis précisez le type de tests que vous avez effectués, précisez les informations sur l’ordre si vous avez effectué des tests de type I et précisez les contrastes si vous avez effectué des tests de type III. Ou, mieux encore, faites des tests d’hypothèses qui correspondent à des choses qui vous tiennent vraiment à cœur, puis rapportez-les !↩︎