Chapitre 5 Réaliser des graphiques

Par-dessus tout, affichez les données. -Edward Tufte³¹

La visualisation des données est l’une des tâches les plus importantes de l’analyste de données. C’est important pour deux raisons distinctes mais étroitement liées. Tout d’abord, il s’agit de dessiner des « représentations graphique », l’affichage de vos données d’une manière propre et visuellement attrayante facilite la compréhension de ce que vous essayez de leur dire par votre lecteur. Le fait que dessiner des graphiques vous aide à comprendre les données est tout aussi important, voire plus important encore. Pour ce faire, il est important de dessiner des « graphiques exploratoires » qui vous aideront à en apprendre davantage sur les données au fur et à mesure que vous les analysez. Ces points peuvent sembler assez évidents, mais je ne peux pas compter le nombre de fois où j’ai vu des gens les oublier.

Pour donner une idée de l’importance de ce chapitre, je veux commencer par une illustration classique de la puissance d’un bon graphique. Pour ce faire, la Figure 5‑1 présente une reproduction de l’une des visualisations de données les plus célèbres de tous les temps. C’est la carte des décès dus au choléra de John Snow en 1854. La carte est élégante dans sa simplicité. En arrière-plan, nous avons un plan des rues qui aide à orienter le spectateur. En haut, on voit un grand nombre de petits points, chacun représentant l’emplacement d’un cas de choléra. Les plus grands symboles indiquent l’emplacement des pompes à eau, étiquetées par leur nom. Même l’inspection la plus superficielle du graphique montre très clairement que la source de l’éclosion est presque certainement la pompe de Broad Street. En montrant ce graphique, le Dr Snow a fait en sorte que la poignée soit retirée de la pompe et a mis fin à l’épidémie qui avait tué plus de 500 personnes. Telle est la puissance d’une bonne visualisation des données.

Les objectifs de ce chapitre sont doubles. Tout d’abord, discuter de plusieurs graphiques assez standard que nous utilisons beaucoup lors de l’analyse et de la présentation des données, et ensuite vous montrer comment créer ces graphiques en Jamovi. Les graphiques eux-mêmes ont tendance à être assez simples, de sorte qu’à certains égards, ce chapitre est assez simple. Là où les gens ont habituellement des difficultés, c’est pour apprendre à produire des graphiques et surtout d’apprendre à produire de bons graphiques. Heureusement, apprendre à dessiner des graphiques avec Jamovi est assez simple tant que vous n’êtes pas trop pointilleux sur l’aspect de votre graphique. Ce que je veux dire en disant cela, c’est que Jamovi offre beaucoup de très bons graphiques par défaut, ou tracés, qui produisent la plupart du temps un graphique propre et de haute qualité. Cependant, dans les cas où vous voudriez faire quelque chose de non standard, ou si vous avez besoin d’apporter des changements très spécifiques à la figure, sachez que les fonctionnalités graphiques de Jamovi ne sont pas encore capables de supporter un travail avancé ou une édition détaillées.

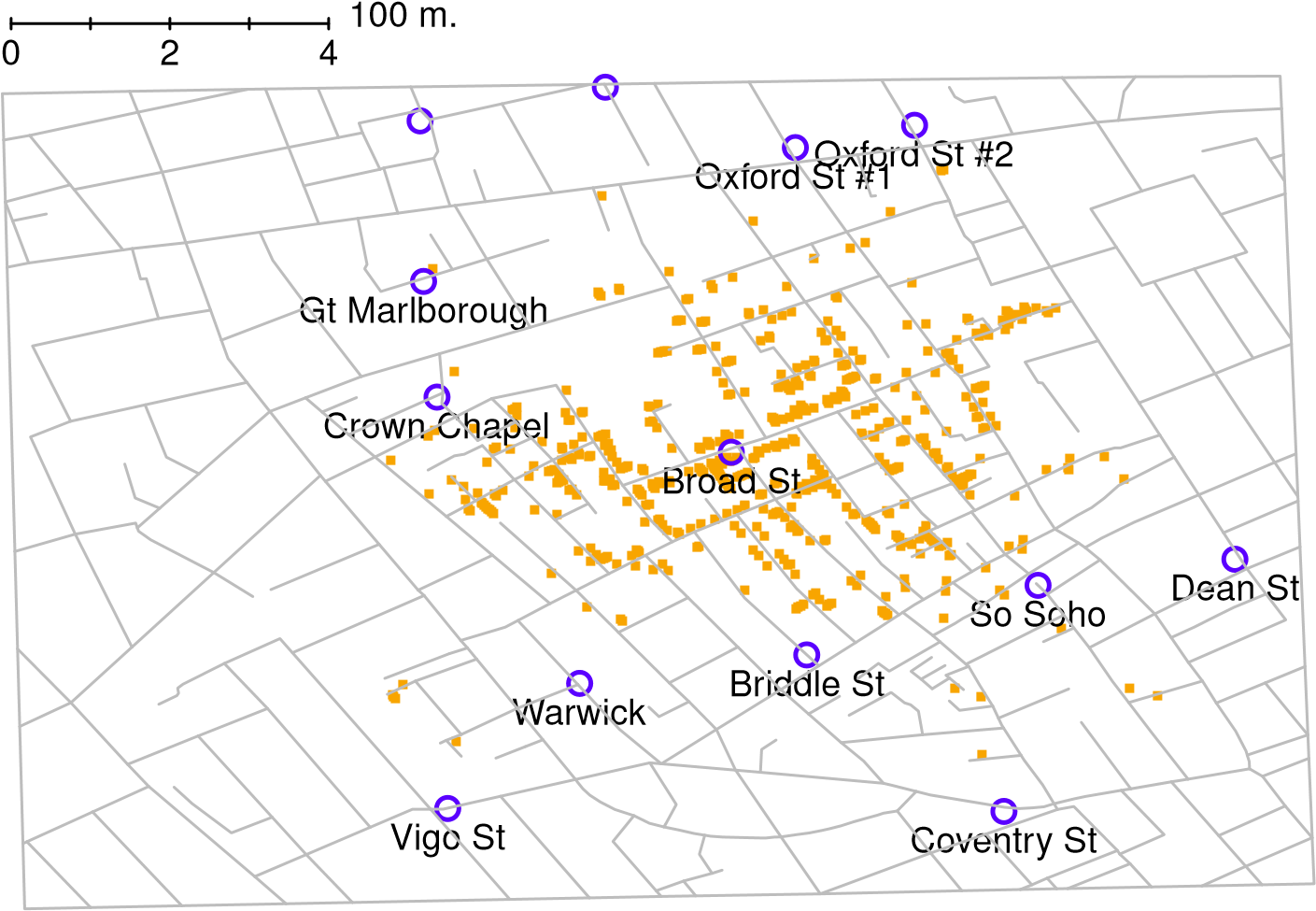
Figure 5‑1 : Une reproduction stylisée de la carte originale de John Snow sur le choléra. Chaque petit point représente l’emplacement d’un cas de choléra et chaque grand cercle indique l’emplacement d’un puits. Comme le montre clairement le graphique, l’épidémie de choléra est centrée très étroitement sur la pompe Broad St.

5.1 Histogrammes

Commençons par l’humble histogramme. Les histogrammes sont l’un des moyens les plus simples et les plus utiles de visualiser les données. Ils sont plus pertinents lorsque vous disposez d’une variable sur une échelle d’intervalle ou de ratio (par exemple, les données de marges afl. du chapitre 4) et que vous voulez obtenir une impression générale de la variable. La plupart d’entre vous savent probablement comment fonctionnent les histogrammes, puisqu’ils sont largement utilisés, mais par souci d’exhaustivité, je vais les décrire. Tout ce que vous faites est de diviser les valeurs possibles en compartiments, puis de compter le nombre d’observations qui tombent dans chaque compartiment. Ce comptage est appelé fréquence ou densité du compartiment et est affiché sous la forme d’une barre verticale. Dans les données sur les marges gagnantes de l’AFL, il y a 33 jeux où la marge gagnante était inférieure à 10 points et c’est ce fait qui est représenté par la hauteur de la barre la plus à gauche que nous avons montrée précédemment au chapitre 4, Figure 4‑2. Avec ces graphiques précédents, nous avons utilisé un package de traçage avancé en R qui, pour l’instant, est au-delà des capacités de Jamovi. Mais Jamovi s’en rapproche, et dessiner cet histogramme en Jamovi est assez simple. Ouvrez les options « tracés » sous « Exploration » - « Descriptives » et cliquez sur la case à cocher « Histogram », comme dans la Figure 5‑2. Jamovi étiquette par défaut l’axe des y « density » et l’axe des x avec le nom de variable. Les compartiments sont sélectionnés automatiquement, et il n’y a pas d’information sur l’échelle, ou de comptage, sur l’axe des y, contrairement à la Figure 4‑2 précédente. Mais cela n’a pas trop d’importance car ce qui nous intéresse vraiment, c’est notre impression sur la forme de la distribution : est-elle normalement distribuée ou y a-t-il une asymétrie ou un aplatissement ? Nos premières impressions sur ces caractéristiques proviennent du tracé d’un histogramme.

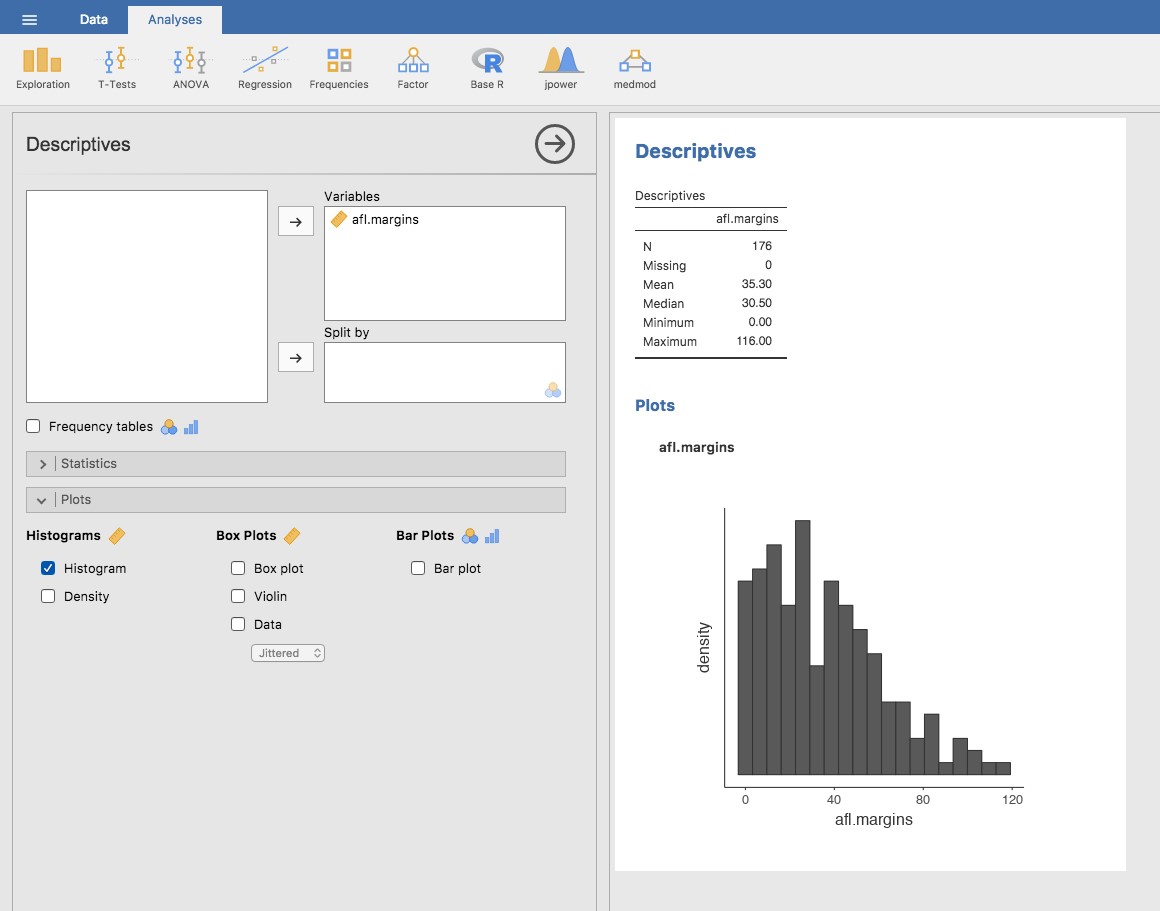
Figure 5‑2 : Ecran Jamovi montrant la case à cocher histogramme

Une caractéristique supplémentaire que Jamovi offre est la possibilité de tracer une courbe de « densité ». Vous pouvez le faire en cliquant sur la case à cocher « Density » sous les options « Graphiques » (et en décochant « Histogramme »), ce qui nous donne le graphique présenté dans la Figure 5‑3. Un graphe de densité visualise la distribution des données sur un intervalle continu ou une période de temps. Ce graphique est une variante d’un histogramme qui utilise l’estimation par noyau pour tracer les valeurs, ce qui permet des distributions plus fines en lissant le bruit. Les pics d’un graphe de densité permettent d’afficher l’endroit où les valeurs sont concentrées sur l’intervalle. L’avantage des courbes de densité par rapport aux histogrammes est qu’elles sont plus aptes à déterminer la forme de distribution parce qu’elles ne sont pas affectées par le nombre de compartiments utilisés (chaque barre utilisée dans un histogramme typique). Un histogramme ne comprenant que 4 compartiments ne produirait pas une forme de distribution suffisamment distincte comme le ferait un histogramme de 20 compartiments. En revanche, dans le cas les graphiques de densité, ce n’est pas un problème.

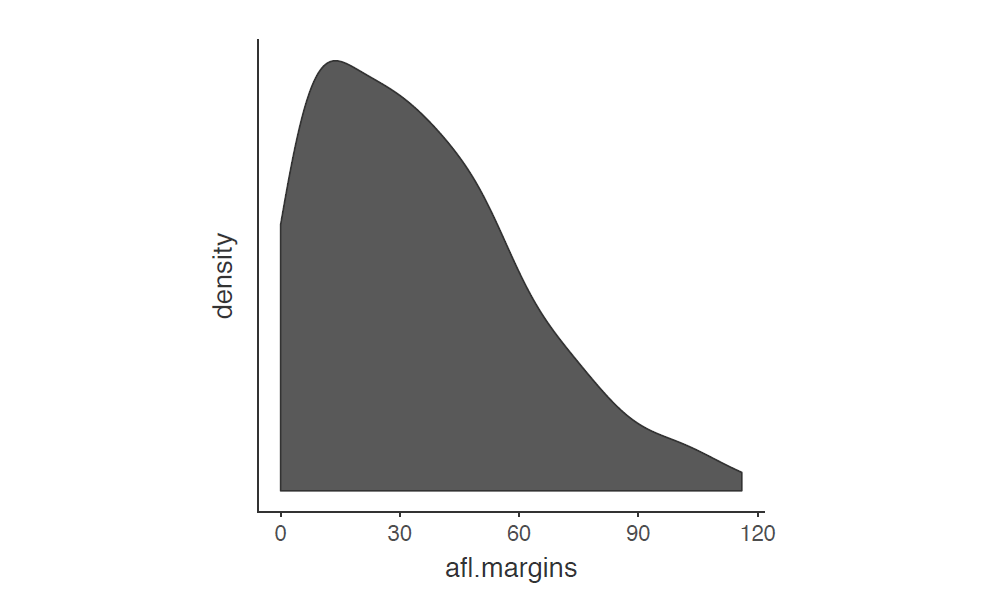
Figure 5‑3 : Un graphe de densité de la variable afl.margins tracé avec Jamovi

Bien que cette image ait besoin de beaucoup de nettoyage pour faire une bonne présentation graphique (c.-à-d. une présentation que vous incluriez dans un rapport), elle fait néanmoins un assez bon travail pour décrire les données. En fait, la grande force d’un histogramme ou d’un graphe de densité est qu’il montre (correctement utilisé) toute la dispersion des données, de sorte que vous pouvez avoir une idée assez précise de ce à quoi elle ressemble. L’inconvénient des histogrammes est qu’ils ne sont pas très compacts. Contrairement à d’autres graphiques, il faut souligner le fait qu’il est difficile d’entasser 20 à 30 histogrammes dans une seule image sans submerger le lecteur. Et bien sûr, si vos données sont à l’échelle nominale, les histogrammes sont inutiles.

5.2 Boxplots

Une autre alternative aux histogrammes est un boxplot, que l’on appelle parfois un tracé « boîte et moustaches ». Comme les histogrammes, ils sont plus adaptés aux données sur une échelle d’intervalle ou de rapport. L’idée derrière un boxplot est de fournir une représentation visuelle simple de la médiane, de l’écart interquartile et de l’étendue des données. Et parce qu’ils le font d’une manière assez compacte, les boxplots sont devenus un graphique statistique très populaire, surtout pendant la phase exploratoire de l’analyse des données lorsque vous essayez de comprendre les données vous-même. Voyons comment ils fonctionnent, encore une fois en utilisant les données afl.margins comme exemple.

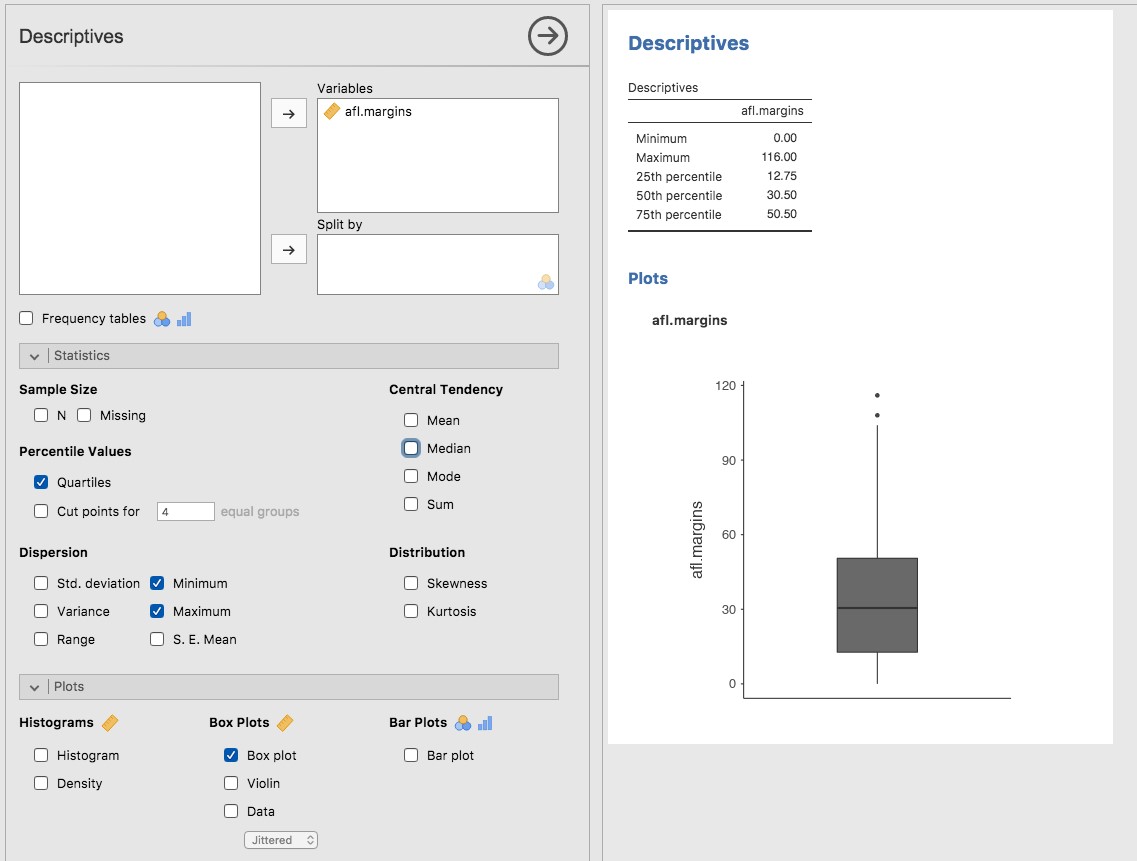
Figure 5‑4 : Un box plot de la variable afl.margins tracée dans Jamovi

La façon la plus simple de décrire à quoi ressemble un boxplot est d’en dessiner un. Cliquez sur la case à cocher « Box plot » et vous obtiendrez le graphique en bas à droite de la Figure 5.4. Jamovi a dessiné le boxplot le plus simple possible. Lorsque vous regardez ce graphique, voici comment vous devez l’interpréter : la ligne épaisse au milieu de la boîte est la médiane ; la boîte elle-même s’étend du 25e centile au 75e centile ; et les « moustaches » vont jusqu’au point de données le plus extrême qui ne dépasse pas une certaine limite. Par défaut, cette valeur est 1,5 fois l’écart interquartile (IQR), calculé comme suit 25e percentile - (1,5*IQR) pour la limite inférieure, et 75e percentile + (1,5*IQR) pour la limite supérieure. Toute observation dont la valeur se situe en dehors de cette plage est tracée sous la forme d’un cercle ou d’un point au lieu d’être couverte par les moustaches, et est communément désignée comme une valeur aberrante. Pour nos données de marges AFL, il y a deux observations qui se situent en dehors de cette plage, et ces observations sont tracées sous forme de points (la limite supérieure est 107, et en regardant au-dessus de la colonne de données dans le tableur, il y a deux observations avec des valeurs supérieures, 108 et 116, ce sont ici les points).

5.2.1 Graphique en violon

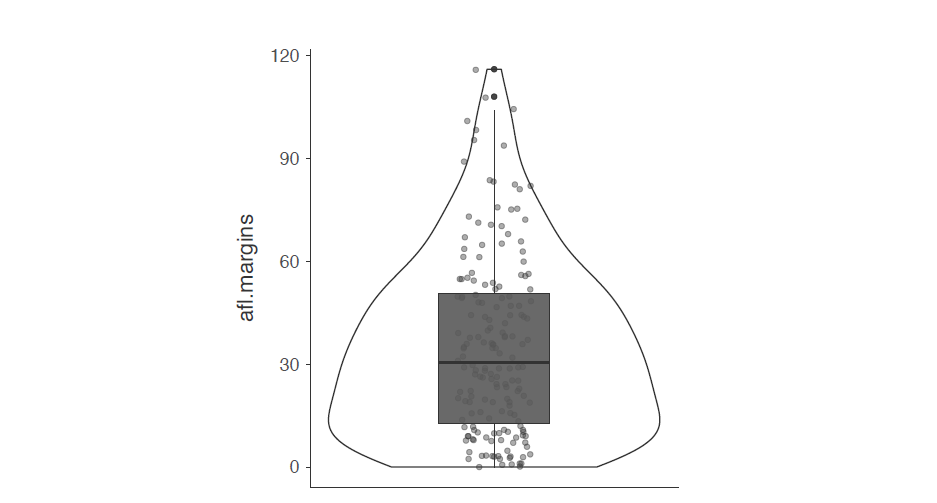
Figure 5‑5 : Un graphique en violon de la variable afl.margins tracé in Jamovi, alsow montrant un tracé en boîte et des points de données.

Le graphique en violon est une variante du box plot traditionnel. Les graphiques en violon sont semblables aux graphiques en boîtes, sauf qu’ils montrent également la densité de probabilité du noyau des données à des valeurs différentes. Habituellement, les graphiques en violon comprennent un marqueur pour la médiane des données et une boite indiquant l’écart interquartile, comme dans les boxplots standards. Dans Jamovi, vous pouvez réaliser ce type de graphiques en cochant les cases « Violin » et « Boxplot ». Voir la Figure 5‑5, où la case à cocher « Data » a également été cochée pour faire apparaitre les points de données réels sur le graphique. Cela tend cependant à rendre le graphique un peu trop surchargé, à mon avis. La clarté est la simplicité, donc dans la pratique, il peut être préférable d’utiliser un simple diagramme en boîtes.

5.2.2 Dessiner plusieurs boxplots

Une dernière chose. Que faire si vous voulez dessiner plusieurs boxplots à la fois ? Supposons, par exemple, que je veuille des boxplots séparés montrant les marges AFL non seulement pour 2010 mais pour chaque année entre 1987 et 2010. Pour ce faire, la première chose à faire est de trouver les données. Ceux-ci sont stockés dans le fichier aflsmall2.csv. Alors chargeons-le dans Jamovi et voyons ce qu’il y a dedans. Vous verrez qu’il s’agit d’un assez grand ensemble de données. Il contient 4296 observations et les variables qui nous intéressent. Ce que nous voulons faire, c’est dessiner des boxplots avec Jamovi pour la variable margin, mais les tracés séparément pour chaque année. Pour ce faire, il suffit de faire glisser la variable année dans la case « Split by », comme dans la Figure 5‑6.

Figure 5‑6 : Capture d’écran de Jamovi montrant la fenêtre « Split by »

Le résultat est illustré à la Figure 5‑7. Cette version du diagramme en boîtes, divisé par année, donne une idée de la raison pour laquelle il est parfois utile de choisir des diagrammes en boîtes plutôt que des histogrammes. Il est possible d’avoir une bonne idée de l’aspect des données d’une année à l’autre sans être submergé par trop de détails. Imaginez maintenant ce qui se serait passé si j’avais essayé d’entasser 24 histogrammes dans cet espace : aucune chance que le lecteur apprenne quelque chose d’utile.

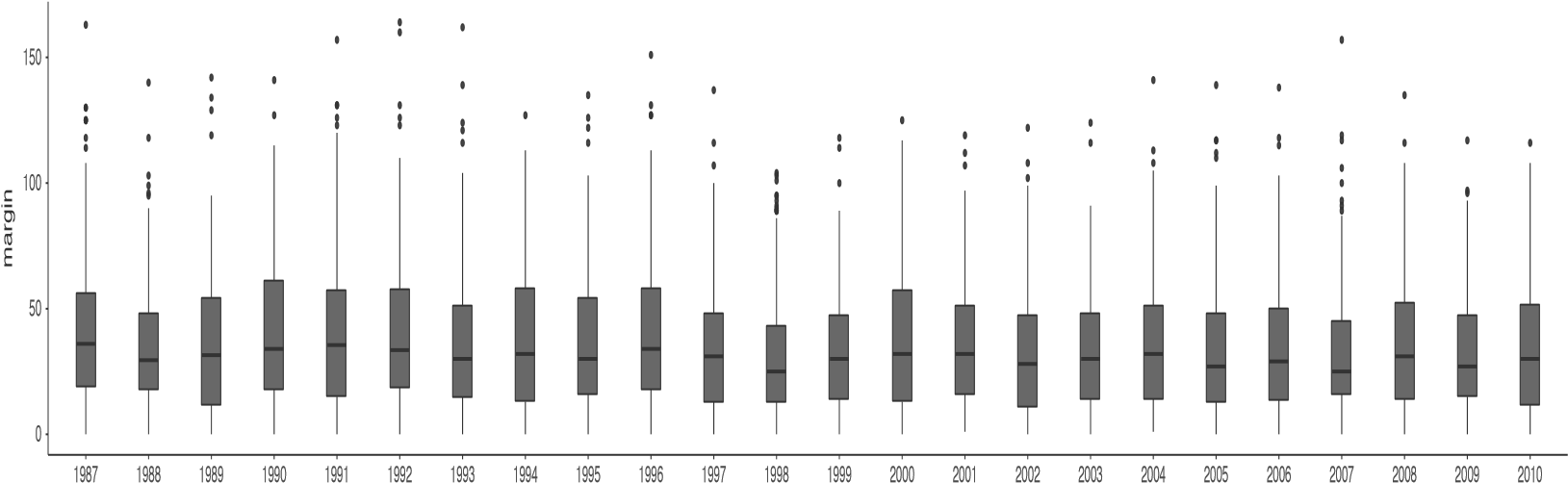
Figure 5‑7 : Boxplots multiples tracés dans Jamovi, pour les variables de marge par année dans l’ensemble de données aflsmall2

5.2.3 Utilisation de diagrammes en boîtes pour détecter les valeurs aberrantes

Parce que le boxplot sépare automatiquement les observations qui se situent en dehors d’une certaine plage, les dépeignant avec un point dans le Jamovi, les gens les utilisent souvent comme une méthode informelle pour la détection des valeurs aberrantes : observations qui sont « étrangement » éloignées du reste des données.

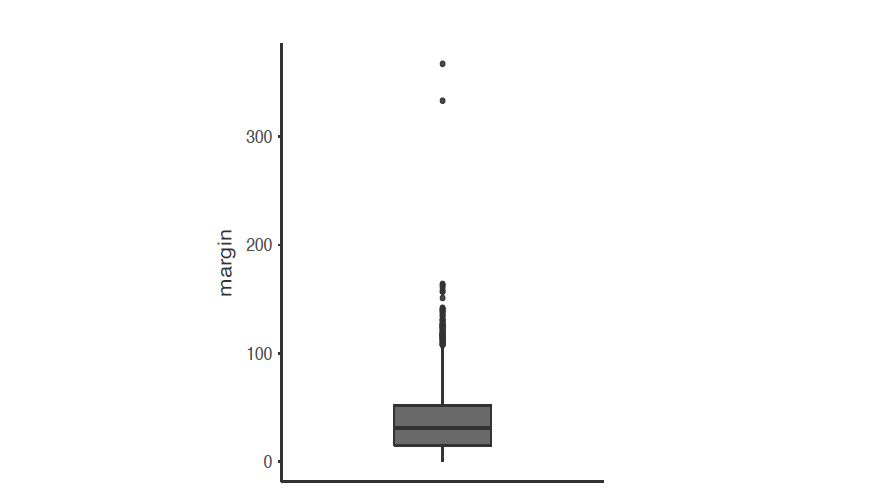
Figure 5‑8 : Un boxplot montrant deux valeurs aberrantes très suspectes !

En voici un exemple. Supposons que j’ai dessiné le boxplot pour les données des marges AFL et qu’il apparaisse comme dans la Figure 5‑8. Il est assez clair qu’il se passe quelque chose de bizarre avec deux des observations. Apparemment, il y a eu deux matchs où la marge était de plus de 300 points ! Ça ne me semble pas correct. Maintenant que j’ai un doute, il est temps d’examiner un peu plus attentivement les données. Dans Jamovi vous pouvez rapidement découvrir lesquelles de ces observations sont suspectes et ensuite vous pouvez retourner aux données brutes pour voir s’il y a eu une erreur dans la saisie des données. Pour ce faire, vous devez configurer un filtre de sorte que seules les observations dont les valeurs dépassent un certain seuil soient incluses. Dans notre exemple, le seuil est supérieur à 300, c’est donc le filtre que nous allons créer. Tout d’abord, cliquez sur le bouton « Filtres » en haut de la fenêtre Jamovi, puis tapez « margin>300 » dans le champ filtre, comme dans la Figure 5‑9.

Ce filtre crée une nouvelle colonne dans la vue feuille de calcul où seules les observations qui passent le filtre sont incluses. Une façon simple d’identifier rapidement ces observations est de dire à Jamovi de produire une « Table de fréquences » (dans la fenêtre « Exploration » - « Descriptives ») pour la variable ID (qui doit être une variable nominale sinon la table de fréquences ne sera pas produite). Dans la Figure 5‑10, vous pouvez voir que les valeurs ID pour les observations où la marge était supérieure à 300 sont 14 et 134. Il s’agit de cas suspects, ou d’observations, où vous devriez retourner à la source de données originale pour savoir ce qui se passe.

Habituellement, vous constatez que quelqu’un a tapé le mauvais chiffre. Bien que cela puisse sembler un exemple stupide, je dois souligner que ce genre de chose arrive souvent. Les ensembles de données du monde réel sont souvent truffés d’erreurs stupides, surtout lorsqu’une personne a dû saisir quelque chose sur un ordinateur à un moment donné. En fait, il y a un nom pour cette phase de l’analyse des données et dans la pratique, cela peut prendre une grande partie de notre temps : le nettoyage des données.

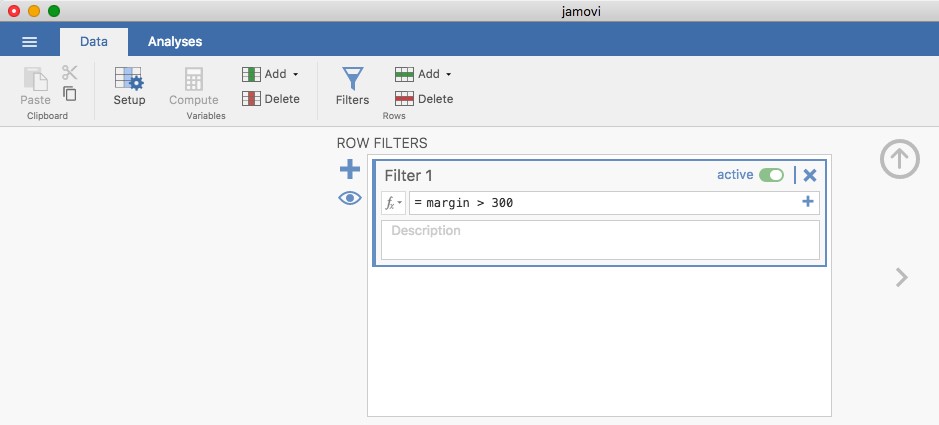
Figure 5‑9 : La grille du filtre Jamovi

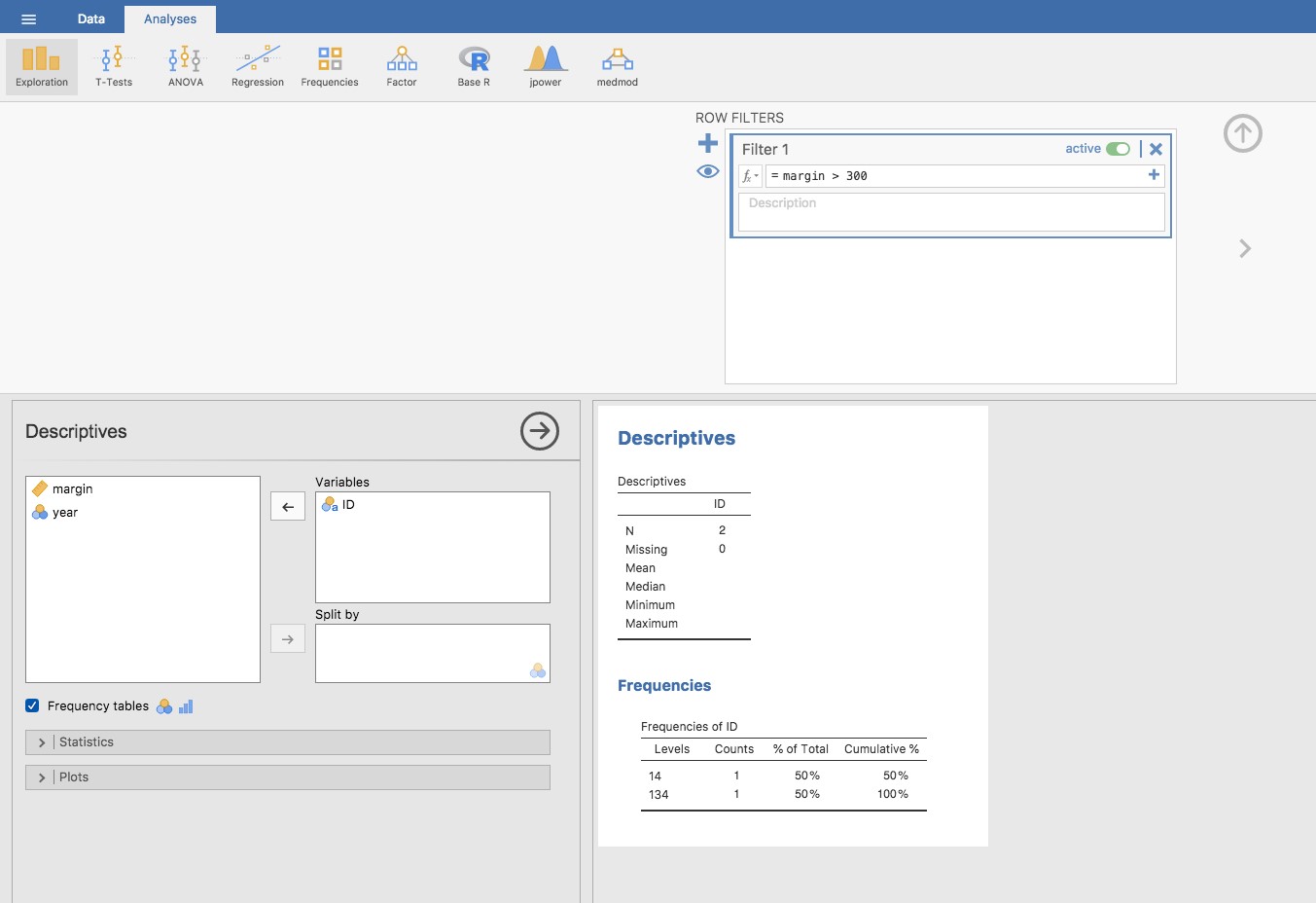
Figure 5‑10 : Tableau de fréquence des numéros d’identification indiquant les numéros d’identification des deux valeurs aberrantes suspectes : 14 et 134

Il s’agit de rechercher les fautes de frappe (« typos »), les données manquantes et toutes sortes d’autres erreurs insupportables dans les fichiers de données brutes.

Pour des valeurs moins extrêmes, même si elles sont marquées dans un boxplot comme valeurs aberrantes, la décision d’inclure ou non des valeurs aberrantes dans une analyse dépend fortement de la raison pour laquelle vous pensez que les données ressemblent à ce qu’elles sont et de l’usage que vous voulez en faire. Vous devez vraiment faire preuve de jugement. Si la valeur aberrante vous semble légitime, gardez-la. Quoi qu’il en soit, je reviendrai sur le sujet à la section 12.10.

5.3 diagramme en barres

Une autre forme de graphique que vous voudrez souvent tracer est le diagramme en barres. Utilisons l’ensemble de données afl.finalists avec la variable afl.finalists que j’ai présentée à la section 4.1.6. Ce que je veux faire, c’est dessiner un graphique en barres qui affiche le nombre de finales auxquelles chaque équipe a participé au cours de la période couverte par l’ensemble de données afl.finalists. Il y a beaucoup d’équipes, mais je suis particulièrement intéressé par quatre d’entre elles : Brisbane, Carlton, Fremantle et Richmond. La première étape consiste donc à mettre en place un filtre pour que seules ces quatre équipes soient incluses dans le diagramme à barres. C’est très simple dans Jamovi et vous pouvez le faire en utilisant la fonction « Filters » que nous avons utilisée précédemment. Ouvrez la fenêtre « Filters » et tapez ce qui suit :

afl.finalistes ==‘Brisbane’ ou afl.finalistes ==‘Carlton’ ou afl.finalistes ==‘Fremantle’ ou afl.finalistes ==‘Richmond’.[Jamovi utilise ici le symbole “==” pour signifier « correspondre »]

Lorsque vous aurez fait cela, vous verrez, dans la vue « Data », que Jamovi a filtré toutes les valeurs à l’exception de celles que nous avons spécifiées. Ensuite, ouvrez la fenêtre « Exploration » - « Descriptives » et cliquez sur la case « Bar plot » (n’oubliez pas de déplacer la variable afl.finalists dans la case « Variables » pour que Jamovi sache quelle variable utiliser). Vous devriez alors obtenir un diagramme à barres, quelque chose comme celui illustré à la Figure 5‑11.

5.4 Enregistrer des fichiers image en utilisant Jamovi

En attendant, vous vous dites peut-être : Quel est l’intérêt de pouvoir dessiner de jolis graphiques avec Jamovi si je ne peux pas les sauvegarder et les envoyer à des amis pour me vanter de l’incroyable qualité de mes données ? Comment sauvegarder l’image ? Simple. Il suffit de cliquer avec le bouton droit de la souris sur l’image du graphique et de l’enregistrer dans un fichier, aux formats « .eps », « svg » ou « pdf ». Ces formats produisent tous de belles images que vous pouvez envoyer à vos amis, ou inclure dans vos devoirs ou papiers.

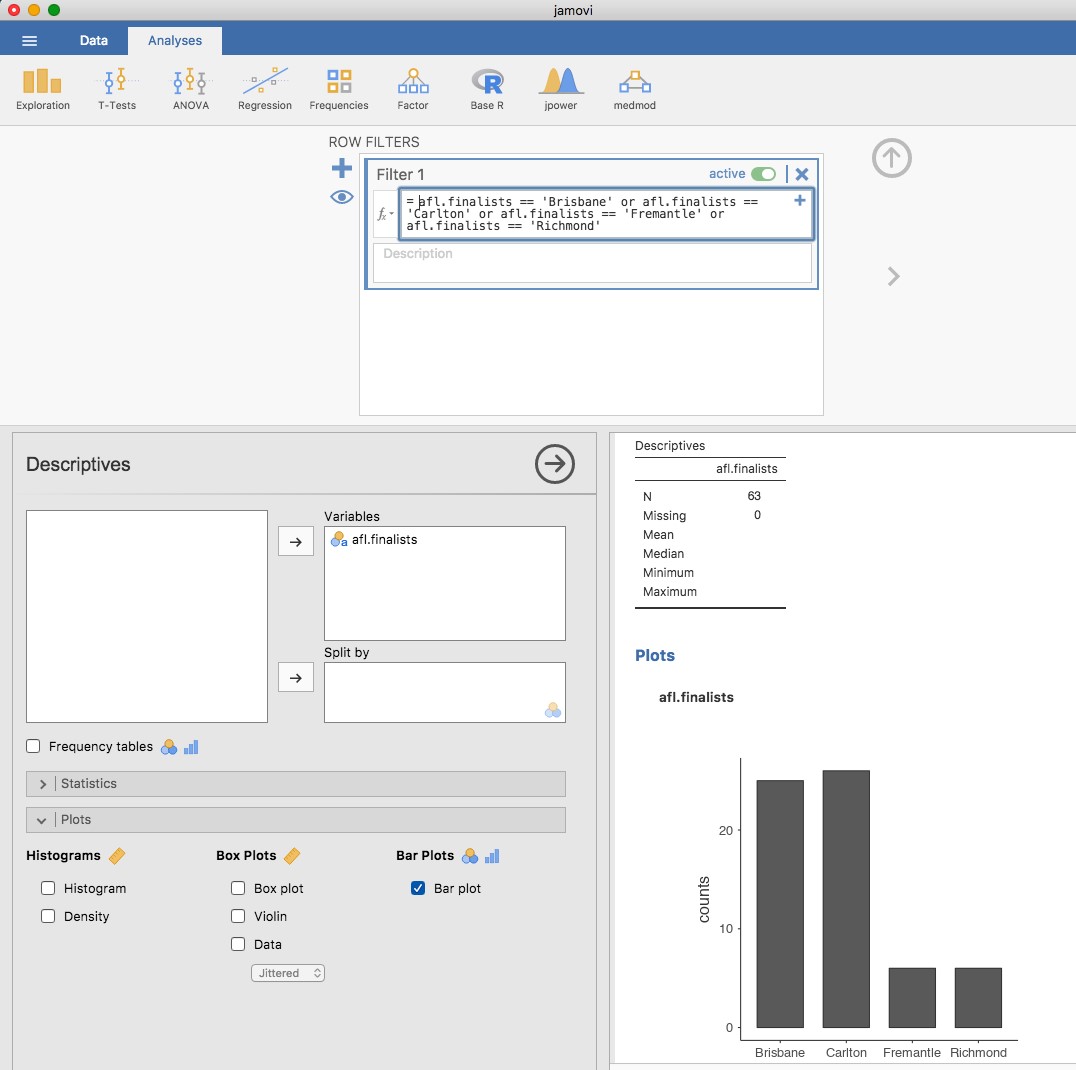
Figure 5‑11 : Filtrage pour n’inclure que quatre équipes de l’AFL, et dessin d’un tracé de bar à Jamovi

5.5 Résumé

Je suis peut-être une personne simple d’esprit, mais j’adore les images. Chaque fois que j’écris un nouvel article scientifique, l’une des premières choses que je fais est de m’asseoir et de réfléchir à ce que seront les illustrations. Dans ma tête, un article n’est en fait qu’une suite d’images reliées entre elles par une histoire. Tout le reste n’est que de la poudre aux yeux. Ce que j’essaie vraiment de dire ici, c’est que le système visuel humain est un outil d’analyse de données très puissant. Donnez-lui le bon type d’information et il fournira très rapidement à un lecteur humain une énorme quantité de connaissances. Ce n’est pas pour rien que nous avons le dicton « une image vaut mille mots ». Dans cet esprit, je pense qu’il s’agit d’un des chapitres les plus importants du livre. Les sujets abordés étaient :

• Graphiques communs. Une grande partie du chapitre a porté sur les graphiques standards que les statisticiens aiment produire : histogrammes (section 5.1), diagrammes de boxplots (section 5.2) et diagrammes en barres (section 5.3).
• Enregistrer des fichiers image. Il est important de noter que nous avons également abordé la façon d’exporter vos photos (Section 5.4)

Une dernière chose à souligner. Bien que Jamovi produise des graphiques par défaut très soignés, l’édition des tracés n’est actuellement pas possible. Pour des graphismes et des capacités de traçage plus avancés, les packages disponibles dans R sont beaucoup plus puissants. L’un des systèmes graphiques les plus populaires est fourni par le paquet ggplot2 (voir http:www//ggplot2.org/), qui est basé sur « The grammar of graphics » (Wilkinson 2005). Ce n’est pas pour les novices. Il faut avoir une bonne maîtrise de R avant de pouvoir commencer à l’utiliser, et même là, il faut un certain temps pour vraiment s’y habituer. Mais quand vous êtes prêt, cela vaut la peine de prendre le temps de vous enseigner, car c’est un système beaucoup plus puissant et plus propre.

References

Wilkinson, Leland. 2005. The Grammar of Graphics. Second. Statistics and Computing. New York: Springer-Verlag. https://doi.org/10.1007/0-387-28695-0.

---

31. L’origine de cette citation est le beau livre de Tufte, The Visual Display of Quantitative Information.↩︎